Aufgabe 3.12: Streng symmetrische Kanäle

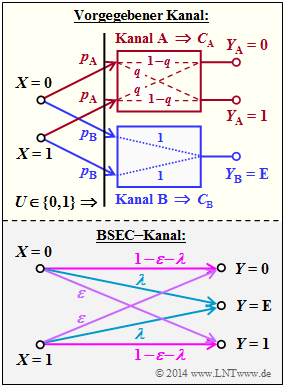
Die obere Grafik zeigt zwei streng symmetrische Teilkanäle A und B. Ein $\text {streng symmetrischer Kanal}$ (englisch: Strongly Symmetric Channel) ist dabei

gleichmäßig $\text{dispersiv }$ (uniformly dispersive) $\Rightarrow$ jedes Eingangssymbol $u$ hat die gleiche Menge an Übergangswahrscheinlichkeiten:

$$\left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{-0.01cm} |\hspace{-0.01cm} u) \hspace{-0.05cm}: \hspace{0.25cm}u \in U \right \} \hspace{0.05cm},$$

zudem gleichmäßig $\text{fokussierend}$ (uniformly focusing)$⇒$jedes Ausgangssymbol y hat die gleiche Übergangswahrscheinlichkeitsmenge:

$$ \left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{-0.01cm} |\hspace{-0.01cm} u) \hspace{-0.05cm}: \hspace{0.25cm}y \in Y \right \} \hspace{0.05cm}.$$ Die Zufallsgröße $U = \{0, 1\}$ tritt dabei direkt an den Eingängen der Teilkanäle $A$ und $B$ auf.

Die Kanalkapazität eines streng symmetrischen Kanals lässt sich sehr viel einfacher berechnen als im unsymmetrischen Fall. Hierauf wird jedoch in dieser Aufgabe nicht näher eingegangen.

Für die Kapazität des Gesamtkanals gilt $$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B}\hspace{0.05cm}$$ Hierbei bezeichnet $p_A$ die Wahrscheinlichkeit, dass der Teilkanal $A$ ausgewählt wird und $C_A$ dessen Kapazität. Entsprechendes gilt für den Teilkanal $B$.

Anschließend soll auch die Kanalkapazität des Binary Symmetric Error & Erasure Channel (BSEC) nach der unteren Skizze (grau hinterlegt) ermittelt werden, indem der Zusammenhang hergeleitet wird zwischen

den Parametern $p_A$, $_pB$ und $q$ des oben dargestelltern Teilkanalmodells, und
den Parametern $λ$ und $ε$ des BSEC–Modells.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 3.3. Entsprechend der Aufgabe Z3.9 gilt für die Kanalkapazität des BSC–Modells mit der Verfälschungswahrscheinlichkeit $ε$: $$ C_{\rm BSC} = 1 - H_{\rm bin}(\varepsilon)\hspace{0.05cm}$$

Fragebogen

Musterlösung

1. Teilkanal $A$ ist ein BSC mit der Verfälschungswahrscheinlichkeit $q ⇒$ Lösungsvorschlag 1.

2. Teilkanal $B$ ist ein Auslöschungskanal. Sowohl die Sinkenentropie als auch die Irrelevanz dieses Teilkanals sind $0 ⇒ C_B = 0 ⇒$ Lösungsvorschlag 3.

3. Die Kapazität C des Gesamtkanals kann mit der angegebenen Gleichung berechnet werden: $$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B} = p_{\rm A} \cdot [1 - H_{\rm bin}(q)]\hspace{0.05cm}.$$ Hier stimmt somit der Lösungsvorschlag 2.

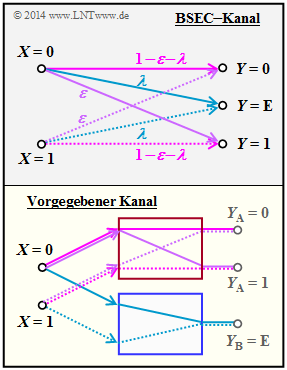
4.Beim bisher betrachteten Modell ergeben sich folgende Übergangswahrscheinlichkeiten: $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) ={\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = p_{\rm B} \hspace{0.05cm}.$$ Beim BSEC–Modell sind die entsprechenden bedingten Wahrscheinlichkeiten gleich $λ ⇒$ siehe $\text{Grafik}$ auf der Angabenseite. Richtig ist also der Lösungsvorschlag 2: $$p_{\rm B} = \lambda = 1 - p_{\rm A} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm A} = 1- \lambda\hspace{0.05cm}.$$ 5. Beim BSEC–Modell gilt beispielsweise: $$ {\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) =\varepsilon \hspace{0.05cm}.$$ Dagegen ergibt sich bei unserem Hilfsmodell $$: {\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) =(1- \lambda) \cdot q \hspace{0.05cm}.$$ Damit erhält man $q = ε/(1 – λ) ⇒$ Lösungsvorschlag 4. Die Grafik verdeutlicht anhand von Farben und Strichart (durchgezogen/gepunktet) den Zusammenhang zwischen beiden Modellen

6.Mit den Ergebnissen der Teilaufgaben (c), (d) und (e) erhält man allgemein: $$C_{\rm BSEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(\frac{\varepsilon}{1- \lambda}) \right ]\hspace{0.05cm},$$ bzw. für $ε = 0.08$ und$λ = 0.2$: $$C_{\rm BSEC} = 0.8 \cdot \left [ 1 - H_{\rm bin}(0.1) \right ] = 0.8 \cdot \left [ 1 - 0.469 \right ] \hspace{0.15cm} \underline {=0.425\,{\rm bit}}\hspace{0.05cm}.$$

7. Der BSC ist ein Sonderfall des BSEC mit λ = 0: $$ C_{\rm BSC} = 1 - H_{\rm bin}(\varepsilon) = 1 - H_{\rm bin}(0.08) = 1 - 0.402 \hspace{0.15cm} \underline {=0.598\,{\rm bit}}\hspace{0.05cm}.$$ 8. Der BEC ist ein Sonderfall des BSEC mit $ε = 0$: $$C_{\rm BEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(0) \right ] = 1- \lambda\hspace{0.05cm}.$$ Mit $λ = 0.2$ ergibt sich hierfür $C_{BEC} = 0.8 bit.$

	$p_A = λ,$
	$p_A = 1 – λ,$
	$p_A = ε$,
	$p_A = ε/(1 – λ)?$

	$q = λ,$
	$q = 1 – λ,$
	$q = ε,$
	$q = ε/(1 – λ)?$

	$C_A = 1 – H_{bin}(q).$
	$C_A = p_A · [1 – H_{bin}(q)].$
	$C_A = 0.$

	$C_B = 1 – H_{bin}(q).$
	$C_B= p_B · [1 – H_{bin}(q)].$
	$C_B = 0.$

	$C = 1 – H_{bin}(q).$
	$C = p_A · [1 – H_{bin}(q)].$
	$C = 0.$