Ursachen und Auswirkungen von Impulsinterferenzen

Definition des Begriffs „Impulsinterferenz” (1)

Für die beiden ersten Kapitel dieses Buches wurde vorausgesetzt, dass der Detektionsgrundimpuls g_d(t)

entweder auf den Zeitbereich |t| ≤ T begrenzt ist, oder
äquidistante Nulldurchgänge im Symbolabstand T aufweist.

Bezeichnen wir die Abtastwerte von g_d(t) bei Vielfachen der Symboldauer T (Abstand der Impulse) als die Detektionsgrundimpulswerte, so wurde in den Kapiteln 1 und 2 stillschweigend vorausgesetzt:

\[g_\nu = g_d(\nu T) = \left\{ \begin{array}{c} g_0 \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\nu = 0, \\ \\ \nu \ne 0. \\ \end{array}\]

Als Konsequenz dieser Annahme hat sich daraus ergeben, dass der Nutzanteil (Index „S”)

\[d_{\rm S}(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_d ( t - \nu \cdot T) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}a_\nu \in \{ -1, +1\}\]

des Detektionssignals zu den Zeitpunkten νT nur zwei verschiedene Werte annehmen kann, nämlich ±g₀.

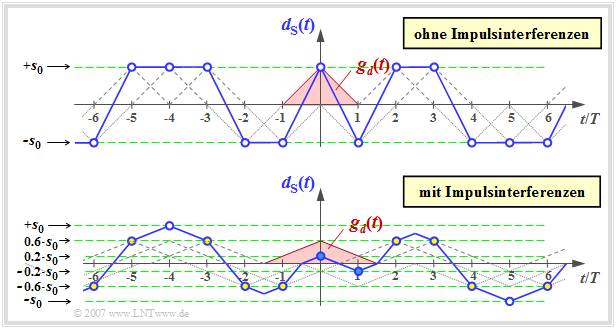
Die obere der beiden Grafiken zeigt d_S(t) für diesen impulsinterferenzfreien Fall mit g₀ = s₀ und g_ν_≠0 = 0. Darunter gezeichnet ist der Signalverlauf für die Detektionsgrundimpulswerte

\[g_0 = 0.6 \cdot s_0, \hspace{0.2cm}g_{-1} = g_{1} =0.2 \cdot s_0, \hspace{0.2cm}g_\nu =0\hspace{0.3cm}{\rm f\ddot{u}r}\hspace{0.3cm} |\nu| \ge 2 \hspace{0.05cm},\]

die Impulsinterferenzen hervorrufen.

In beiden Bildern ist der (jeweils dreieckförmige) Detektionsgrundimpuls g_d(t) rot eingezeichnet. Die Detektionszeitpunkte νT sind jeweils durch blaue Kreise markiert. Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.

Definition des Begriffs „Impulsinterferenz” (2)

Man erkennt aus dem unteren Signalverlauf auf der vorherigen Seite:

Der Detektionsgrundimpuls g_d(t) ist nun im Bereich |t| ≤ 1.5T von Null verschieden und erfüllt somit nicht mehr die Nyquist–Bedingung der Impulsinterferenzfreiheit.

Dies hat zur Folge, dass zu den (mit Kreisen markierten) Detektionszeitpunkten nicht nur zwei Werte (±s₀) möglich sind wie im oberen Bild. Vielmehr gilt für die Detektionsnutzabtastwerte:

\[d_{\rm S}(\nu \cdot T) \in \{ \pm s_0, \pm 0.6 s_0,\pm 0.2 s_0\}\hspace{0.05cm}.\]

Die Abtastwerte, die aufgrund ungünstiger Nachbarimpulse nahe an der Schwelle liegen, werden durch das AWGN–Rauschen (mit Rauscheffektivwert σ_d) häufiger verfälscht als die weiter außen liegenden Abtastwerte.

Beispielhaft werden mit σ_d/s₀ = 0.2 die blau ausgefüllten Punkte nahe der Schwelle mit großer Wahrscheinlichkeit p_S = Q(1) ≈ 16% verfälscht und die äußeren Punkte (mit weißem Kern) nur mit p_S = Q(5) ≈ 3 · 10^–7. Die Fehlerwahrscheinlichkeit der gelb gefüllten Punkte (alle im Abstand 0.6 · s₀ von der Null–Linie) liegt dazwischen:

\[p_{\rm S} ={\rm Q} (3) \approx 0.13 \% \hspace{0.05cm}.\]

Bisher wurden die Auswirkungen von Impulsinterferenzen möglichst anschaulich dargelegt. Es fehlt noch eine exakte Begriffsbestimmung.

: Unter Impulsinterferenz (englisch: Intersymbol Interference, ISI) versteht man die Beeinträchtigung einer Symbolentscheidung aufgrund einer Impulsverbreiterung (Zeitdispersion) und damit verbunden eine Abhängigkeit der Fehlerwahrscheinlichkeit von den Nachbarsymbolen.

In anderen Worten:

Durch abfallende Flanken vorangegangener Impulse („Nachläufer”) und ansteigende Flanken folgender Impulse („Vorläufer”) wird der momentan anliegende Detektionsabtastwert verändert.

Dadurch kann die Wahrscheinlichkeit einer Fehlentscheidung für das aktuelle Symbol vergrößert oder verkleinert werden, je nachdem, ob der Abstand zur Schwelle kleiner oder größer wird.

Im statistischen Mittel – also bei Betrachtung einer (unendlich) langen Symbolfolge – führt dies stets zu einer (beträchtlichen) Erhöhung der (mittleren) Symbolfehlerwahrscheinlichkeit p_S.

[[Datei:||class=fit]]