Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen
Gaußförmiges Empfangsfilter (1)
Zur quantitativen Berücksichtigung der Impulsinterferenzen wird folgende Konfiguration angenommen:
- Rechteckförmiger NRZ–Sendegrundimpuls gs(t) mit der Höhe s0 und der Dauer T,
- Gaußförmiges Empfangsfilter mit der Grenzfrequenz fG:
- \[H_{\rm E}(f) = H_{\rm G}(f) = {\rm exp}\left [- \frac{\pi \cdot f^2}{(2f_{\rm G})^2} \right ] \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm}h_{\rm E}(t) = h_{\rm G}(t) = {\rm exp}\left [- \pi \cdot (2 f_{\rm G} t)^2\right ] \hspace{0.05cm}.\]
- AWGN–Kanal, das heißt, es gilt HK(f) = 1 und Φn(f) = N0/2.
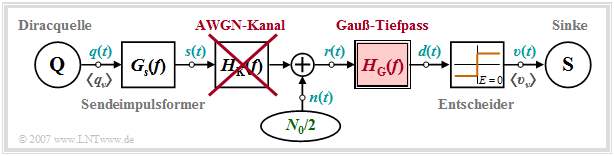
Für das gesamte Kapitel 3.2 wird somit von nachfolgendem Blockschaltbild ausgegangen.
Aufgrund der getroffenen Voraussetzungen gilt für den Detektionsgrundimpuls:
\[g_d(t) = g_s(t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot s_0 \cdot \int_{t-T/2}^{t+T/2} {\rm exp}\left [- \pi \cdot (2 \cdot f_{\rm G}\cdot \tau )^2\right ] \,{\rm d} \tau \hspace{0.05cm}.\]
Die Integration führt zu folgendem Ergebnis:
\[g_d(t) = s_0 \cdot \left [ {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \right ]\hspace{0.05cm},\]
\[g_d(t) = {s_0}/{2} \cdot \left [ {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \right ]\hspace{0.05cm}.\]
Hierbei sind zwei Varianten der komplementären Gaußschen Fehlerfunktion verwendet, nämlich
\[\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm},\hspace{0.5cm} {\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.\]
Das Modul QFunction.swf Komplementäre Gaußsche Fehlerfunktion liefert die Zahlenwerte von Q(x) und erfc(x).
Die Rauschleistung am Ausgang des gaußförmigen Empfangsfilters HG(f) ist gleich
\[\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0\cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.\]
Aus diesen beiden Gleichungen erkennt man bereits:
- Je kleiner die Grenzfrequenz fG des Gauß–Tiefpasses ist, desto kleiner ist der Rauscheffektivwert σd und umso besser ist demzufolge das Rauschverhalten.
- Eine kleine Grenzfrequenz führt aber zu einer starken Abweichung des Detektionsgrundimpulses gd(t) von der Rechteckform und damit zu nicht vernachlässigbaren Impulsinterferenzen.
Next
[[Datei:||class=fit]]