Entscheidungsrückkopplung

1. Digitalsignalübertragung
2. Impulsinterferenzen und Entzerrungsverfahren
3. Entscheidungsrückkopplung

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Prinzip und Blockschaltbild

Eine Möglichkeit zur Verminderung von Impulsinterferenzen bietet die Entscheidungsrückkopplung (engl.: Decision Feedback Equalization – abgekürzt DFE). In der deutschsprachigen Literatur wird diese manchmal auch als Quantisierte Rückkopplung (QR) bezeichnet.

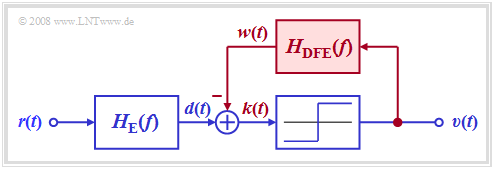
Die Grafik zeigt den entsprechenden Empfänger. Man erkennt anhand des Blockschaltbildes:

• Ohne die rot eingezeichnete Signalrückführung ergäbe sich ein herkömmlicher Digitalempfänger mit Schwellenwertentscheidung entsprechend Kapitel 3.3. Für die nachfolgende Beschreibung wird wieder angenommen, dass sich das gesamte Empfangsfilter H_E(f) aus dem Kanalentzerrer 1/H_K(f) und einem Gaußtiefpass H_G(f) zur Rauschleistungsbegrenzung zusammensetzt.
  

• Beim Empfänger mit Entscheidungsrückkopplung wird vom rechteckförmigen Ausgangssignal υ(t) über ein lineares Netzwerk mit dem Frequenzgang H_DFE(f) ein Kompensationssignal w(t) gewonnen und an den Eingang des Schwellenwertentscheiders zurückgeführt.
  

• Dieses Signal w(t) wird vom vorentzerrten Signal d(t) subtrahiert. Bei geeigneter Dimensionierung des Rückkopplungsnetzwerkes weist somit das korrigierte Signal k(t) = d(t) – w(t) keine (oder zumindest deutlich geringere) Impulsnachläufer auf als das Signal d(t). Die Impulsvorläufer können dagegen aus Kausalitätsgründen nicht beeinflusst werden.
  

• Da bei diesem Empfänger mit Entscheidungsrückkopplung das Kompensationssignal w(t) vom rauschfreien Sinkensignal υ(t) abgeleitet wird, ist die Signalentzerrung nicht mit einer Erhöhung der Rauschleistung verbunden wie bei linearer Entzerrung. Vielmehr besitzt das korrigierte Signal k(t) den gleichen Rauscheffektivwert σ_d wie das Signal d(t).
  
  

Hinweis: Die Signalverläufe dieses nichtlinearen Entzerrungsverfahrens „DFE” sowie die zugehörigen Fehlerwahrscheinlichkeiten – gültig für einen verzerrungsfreien Kanal – können mit dem folgenden Interaktionsmodul angezeigt werden:
Entscheidungsrückkopplung

Ideale Entscheidungsrückkopplung

Wir behandeln zunächst die ideale DFE–Realisierung anhand der Grundimpulse.

: Eine ideale Entscheidungsrückkopplung liegt vor, wenn am Entscheider der folgende Grundimpuls anliegt: \[g_k(t) = \left\{ \begin{array}{c} g_d(t) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} t < T_{\rm D} + T_{\rm V}, \\ t \ge T_{\rm D} + T_{\rm V}. \\ \end{array}\]

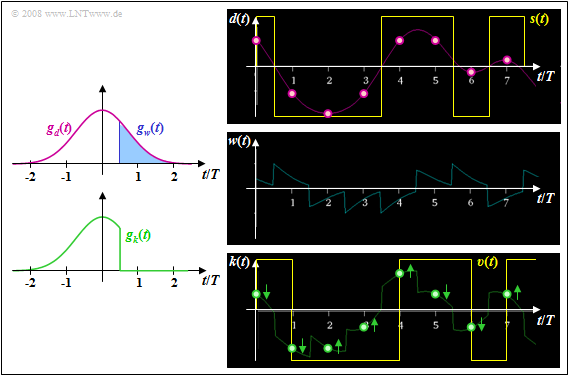
Das bedeutet, dass im Idealfall der Kompensationsgrundimpuls g_w(t) den linear vorentzerrten Impuls g_d(t) für alle Zeiten t > T_D + T_V exakt nachbilden muss. Die aus Realisiserungsgründen erforderliche Verzögerungszeit T_V muss stets kleiner als die Symboldauer T sein; im Folgenden gelte stets T_V = T/2.

: Der Gesamtfrequenzgang H_K(f) · H_E(f) = H_G(f) sei gaußförmig mit der Grenzfrequenz f_G = 0.3/T. Bei NRZ–Rechteckimpulsen ergibt sich dann der skizzierte Detektionsgrundimpuls g_d(t).

Links dargestellt sind auch die Grundimpulse g_w(t) und g_k(t) bei idealer Entscheidungsrückkopplung, wobei der Detektionszeitpunkt T_D = 0 und die Verzögerungszeit T_V = T/2 zugrunde liegen.

Die rechten Bilder aus Söder, G.: Simulation digitaler Übertragungssysteme. Anleitung zum gleichnamigen Praktikum. Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2001 – alle ohne Berücksichtigung des Rauschens – machen deutlich, dass durch die Kompensation aller Impulsnachläufer mittels des Korrektursignals w(t) die Abstände der Nutzabstandswerte d_S(νT) von der Entscheiderschwelle E = 0 verändert werden. Besonders geringe Abstände wie beispielsweise zu den Zeitpunkten t = 6T und t = 7T werden deutlich vergrößert und damit deren Fehlerwahrscheinlichkeiten stark verringert (Pfeile weggehend von der Schwelle).

Dagegen werden die im Signal d(t) weit vom Schwellenwert E = 0 entfernten Detektionsabtastwerte zur Schwelle hin verschoben und deren Verfälschungswahrscheinlichkeit leicht erhöht. Dies erkennt man zum Beispiel für den Zeitpunkt t = 5T.

Augenöffnung und Fehlerwahrscheinlichkeit bei DFE

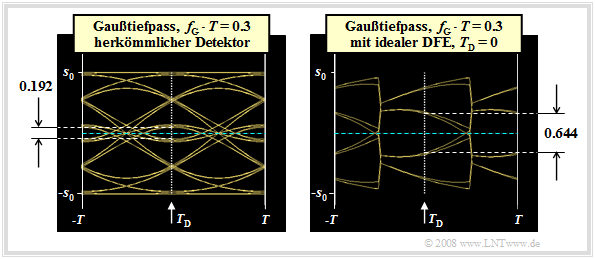
Betrachten wir nun die Augendiagramme ohne DFE (linke Grafik) und mit idealer DFE (rechte Grafik).

Dabei wird von den gleichen Voraussetzungen wie auf der letzten Seite ausgegangen, so dass folgende Grundimpulswerte vorliegen:

\[g_0 = g_d(t=0) = 0.548 \cdot s_0 \hspace{0.05cm},\hspace{0.2cm}g_1 = g_d(t=T) = 0.214 \cdot s_0 = g_{-1} \hspace{0.05cm},\] \[ g_2 = g_d(t=2\hspace{0.05cm}T) = 0.012 \cdot s_0 = g_{-2} \hspace{0.05cm},\hspace{0.2cm}g_3 = g_{-3} = ... \approx 0 \hspace{0.05cm}.\]

Diese beiden Augendiagramme können wie folgt interpretiert werden:

• Beim herkömmlichen Empfänger (ohne DFE) gilt bei binärer bipolarer redundanzfreier Codierung unter Berücksichtigung der Symmetrie:

\[{\ddot{o}(T_{\rm D} = 0 )} = {2} \cdot \left [ g_0 - | g_{-1}| - | g_{-2}| - | g_{1}| - | g_{2}|\right ] =\]

\[ = {2} \cdot \left [ g_0 - 2 \cdot g_{1} - 2 \cdot g_{2}\right ]= 0.192 \cdot s_0 \hspace{0.05cm}.\]

• Dagegen werden bei idealer DFE die beiden Nachläufer g₁ und g₂ vollständig kompensiert und man erhält für die vertikale Augenöffnung:

\[{\ddot{o}(T_{\rm D} = 0 )} = {2} \cdot \left [ g_0 - g_{-1} - g_{-2}\right ]= 0.644 \cdot s_0 \hspace{0.05cm}.\]

• Da das Korrektursignal w(t) aus dem entschiedenen und damit rauschfreien Signal υ(t) abgeleitet wird, wird der Rauscheffektivwert durch die Entscheidungsrückkopplung nicht verändert. Der Störabstandsgewinn durch die DFE ist somit im betrachteten Beispiel gleich

\[G_{\rm DFE}= 20 \cdot {\rm lg}\hspace{0.1cm}\frac{0.644}{0.192} \approx 10.5\,{\rm dB} \hspace{0.05cm}.\]

Bei einem Koaxialkabel mit charakteristischer Kabeldämpfung a_∗ = 80 dB und 10 · lg E_B/N₀ = 80 dB bedeutet dieser Störabstandsgewinn beispielsweise, dass die ungünstigste Fehlerwahrscheinlichkeit p_U durch die DFE von 7% auf ca. 4 · 10^–7 verkleinert wird – eine durchaus beachtenswerte Verbesserung.

Optimierung eines Übertragungssystems mit DFE

Die letzte Seite hat deutlich gemacht, dass die Entscheidungsrückkopplung bereits dann einen enormen Störabstandsgewinn bewirkt, wenn von einer festen Grenzfrequenz f_G und dem Detektionszeitpunkt T_D = 0 ausgegangen wird. Das System lässt sich aber weiter verbessern, wenn die beiden Parameter f_G und T_D gemeinsam optimiert werden.

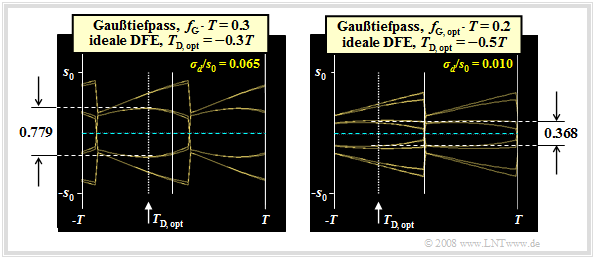
Betrachten wir die Augendiagramme ohne Rauschen für f_G · T = 0.3 (links) und f_G · T = 0.2 (rechts). Für die nachfolgenden Berechnungen werden weiterhin die charakteristische Kabeldämpfung a_∗ = 80 dB sowie der AWGN–Parameter 10 · lg E_B/N₀ = 80 dB (mit E_B = s₀² · T) vorausgesetzt, so dass sich der normierte Rauscheffektivwert zu σ_d/s₀ = 0.065 (für f_G · T = 0.3) bzw. σ_d/s₀ = 0.010 (für f_G · T = 0.2) ergibt. Die Optimierungsergebnisse lassen sich wie folgt zusammenfassen:

• Mit f_G · T = 0.3 kann durch Verschiebung des Detektionszeitpunktes auf T_D,opt = –0.3T die Augenöffnung auf ö(T_D) = 0.779 · s₀ vergrößert werden. Daraus resultiert gegenüber T_D = 0 (vergleiche letze Seite) ein weiterer Störabstandsgewinn von 20 · lg (0.779/0.644) ≈ 1.65 dB und die Fehlerwahrscheinlichkeit ergibt sich nun zu p_U ≈ 1.3 · 10^–9 (gegenüber 4 · 10^–7).
  

• Bei einem DFE–Empfänger kann man zusätzlich die Grenzfrequenz weiter herabsetzen. So ergibt sich mit f_G · T = 0.2 und T_D = 0 die zwar kleine, aber immerhin von 0 verschiedene Augenöffnung ö(T_D) = 0.152 · s₀, die zusammen mit dem sehr günstigen Rauscheffektivwert σ_d/s₀ = 0.010 zum (ungünstigsten) Störabstand 17.6 dB und zur Fehlerwahrscheinlichkeit p_U = 1.6 · 10^–14 führt.
  

• Durch Kombination der Grenzfrequenz f_G · T = 0.2 mit dem Detektionszeitpunkt T_D = –0.5T erhält man schließlich die bei den getroffenen Voraussetzungen optimale Systemkonfiguration mit der Augenöffnung ö(T_D) = 0.368 · s₀ und dem (ungünstigsten) Störabstand 10 · lg ρ_U = 25.3 dB. Die Fehlerwahrscheinlichkeit ist damit (praktisch) gleich 0.