Aufgabe 2.2: Modulationsgrad
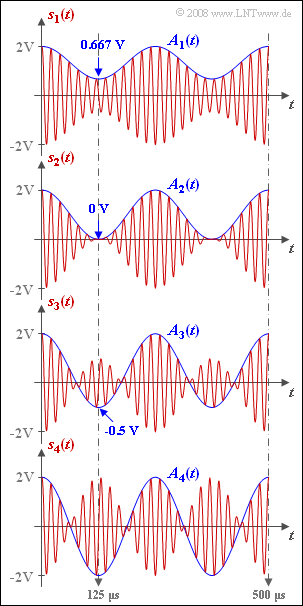
Die Grafik zeigt ZSB–amplitudenmodulierte Signale $s_1(t)$ bis $s_4(t)$ mit unterschiedlichem Modulationsgrad. Das Nachrichtensignal $q(t)$ und das Trägersignal $z(t)$ seien jeweils cosinusförmig: $$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$ $$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$ Das modulierte Signal (Sendesignal) lautet somit mit dem im Modulator zugesetzten Gleichanteil $A_T$: $$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ Ist der Modulationsgrad m ≤ 1, so ist A(t) gleich der Hüllkurve a(t). Dagegen gilt für m > 1: $$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$ Der cosinusförmige Verlauf $A(t)$ schwankt zwischen $A_{max}$ und $A_{min}$, wobei wegen der obigen Normierung stets $A_{max} = 2V$ ist. Die Minimalwerte von $A(t)$ treten zum Beispiel bei der halben Periodendauer des Quellensignals (also für $t = 125 μs$) auf: $$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$ Die Zahlenwerte sind in der Grafik angegeben.
Hinweis:Die Aufgabe bezieht sich auf den Theoriteil von Kapitel 2.1.
Fragebogen
Musterlösung