Aufgabe 4.16: Vergleich zwischen binärer PSK und binärer FSK

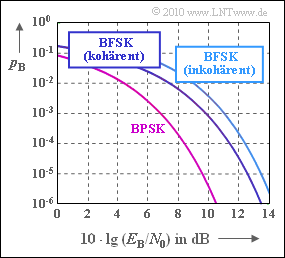
Die Grafik zeigt die Bitfehlerwahrscheinlichkeit für eine binäre FSK–Modulation bei

im Vergleich zur binären Phasenmodulation (BPSK). Es wird stets Orthogonalität vorausgesetzt. Bei kohärenter Demodulation kann hierbei der Modulationsindex h ein Vielfaches von 0.5 sein, so dass die mittlere Kurve auch für Minimum Shift Keying (MSK) gültig ist. Dagegen muss bei nichtkohärenter Demodulation einer FSK der Modulationsindex h ein Vielfaches von 1 sein.

Diesem Systemvergleich liegt wieder der sog. AWGN–Kanal zugrunde, gekennzeichnet durch das Verhältnis $E-B/N_0$. Die Gleichungen für die Bitfehlerwahrscheinlichkeiten lauten bei

Binary Phase Shift Keying (BPSK):

$$p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \frac{1}{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ),$$

Binary Frequency Shift Keying (BFSK) mit kohärenter Demodulation:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \frac{1}{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \hspace{0.1cm}\right ),$$

Binary Frequency Shift Keying (BFSK) mit inkohärenter Demodulation:

$$p_{\rm B} = \frac{1}{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$ In Aufgabe A4.7 wurde gezeigt, dass bei BPSK das logarithmierte Verhältnis $10 · lg E_B/N_0$ mindestens 9.6 dB betragen muss, damit die Bitfehlerwahrscheinlichkeit den Wert $p_B = 10^{–5}$ nicht überschreitet.

Hinweis: Die Aufgabe behandelt die Thematik von Kapitel 4.2 und Kapitel 4.4. Verwenden Sie die Näherung $lg(2) ≈ 0.3$.

Fragebogen

$MSK, \text{kohärent}: 10 · lg E_B/N_0$ =

$dB$

	einer FSK mit Modulationsindex $η = 0.7$,
	einer FSK mit Modulationsindex $η = 1$?

$FSK, \text{inkohärent}: 10 · lg E_B/N_0$ =

$dB$

$FSK, \text{inkohärent}: p_B$ =

$10^{-4}$

Musterlösung

1. Ein Vergleich der beiden ersten Gleichungen auf der Angabenseite macht deutlich, dass bei der MSK mit kohärenter Demodulation das AWGN–Verhältnis $E_B/N_0$ verdoppelt werden muss, damit die gleiche Fehlerwahrscheinlichkeit wie bei BPSK erreicht wird. In anderen Worten: Die kohärente BFSK–Kurve liegt um $10 · lg (2) ≈ 3 dB$ rechts von der BPSK–Kurve. Um $p_B ≤ 10^{–5}$ zu garantieren, muss gelten: $$10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}} /{N_{\rm 0}}= 9.6\,\,{\rm dB} + 3\,\,{\rm dB} = \underline{12.6\,\,{\rm dB}}\hspace{0.05cm}.$$

2. Die angegebene Gleichung gilt nicht nur für die MSK (diese ist eine FSK mit $η = 0.5$), sondern für jede Form von orthogonaler FSK. Eine solche liegt vor, wenn der Modulationsindex η ein ganzzahliges Vielfaches von 0.5 ist, zum Beispiel für $η = 1$. Mit $η = 0.7$ ergibt sich keine orthogonale FSK. Es kann gezeigt werden, dass sich für $η = 0.7$ sogar eine kleinere Fehlerwahrscheinlichkeit als bei orthogonaler FSK ergibt. Mit $10 · lg E_B/N_0 = 12.6 dB$ erreicht man hier sogar $p_B ≈ 10^{–6}$, also eine Verbesserung um eine Zehnerpotenz. Richtig ist demzufolge der Lösungsvorschlag 2.

3. Aus der Umkehrfunktion der angegebenen Gleichung erhält man: $$\frac{E_{\rm B}} {2 \cdot N_{\rm 0}}= {\rm ln}\hspace{0.05cm}\frac{1}{2 p_{\rm B}}= {\rm ln}(50000)\approx 10.82$$ $$\Rightarrow \hspace{0.3cm}{E_{\rm B}} /{N_{\rm 0}}= 21.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}}/ {N_{\rm 0}}\approx \underline{13.4\,\,{\rm dB}}\hspace{0.05cm}.$$

4. Aus $10 · lg E_B/N_0 = 12.6 dB$ folgt: $${E_{\rm B}} /{N_{\rm 0}}= 10^{1.26} \approx 16.8 \hspace{0.25cm}\Rightarrow \hspace{0.25cm} ({E_{\rm B}} /{N_{\rm 0}})/2 \approx 8.4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} p_{\rm B} = {1}/{2} \cdot {\rm e}^{- 8.4} \approx \underline{1.12 \cdot 10^{-4}}\hspace{0.05cm}.$$ Das heißt: Bei gleichem $E_B/N_0$ wird die Fehlerwahrscheinlichkeit bei der inkohärenten Demodulation gegenüber kohärenter Demodulation (siehe Teilaufgabe a) um etwa den Faktor 11 vergrößert.