Fast-Fouriertransformation (FFT)

Inhaltsverzeichnis

1 Rechenaufwand von DFT bzw. IDFT
2 Überlagerungssatz der DFT
3 Radix-2-Algorithmus nach Cooley und Tukey
4 Aufgabe zum Kapitel

Rechenaufwand von DFT bzw. IDFT

Ein Nachteil der direkten Berechnung der (im Allgemeinen komplexen) DFT–Zahlenfolgen

$$<D(\mu)> \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} <d(\nu)>$$

gemäß den in Kapitel Diskrete Fouriertransformation (DFT) angegebenen Gleichungen ist der große Rechenaufwand. Wir betrachten als Beispiel die DFT, also die Berechnung der $D(\mu)$ aus den $d(\nu)$:

$$\begin{align*}N \cdot D(\mu) & = \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} =\\ & = d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+ ... + d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}\end{align*}$$

Der hierfür erforderliche Rechenaufwand soll nun abgeschätzt werden, wobei wir davon ausgehen, dass die Potenzen des komplexen Drehfaktors $w = {\rm e}^{–{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$ bereits in Real– und Imaginärteilform in einer Lookup–Tabelle vorliegen:

Zur Berechnung eines einzelnen Koeffizienten benötigt man dann $N-1$ komplexe Multiplikationen und ebenso viele komplexe Additionen, wobei zu beachten ist:
Jede komplexe Addition erfordert zwei reelle Additionen:

$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.05cm}.$$

Jede komplexe Multiplikation erfordert vier reelle Multiplikationen und zwei reelle Additionen (eine Subtraktion wird wie eine Addition behandelt):

$$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.05cm}.$$

Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich:

$$M = 4 \cdot N \cdot (N-1), \hspace{0.2cm}A = 2 \cdot N \cdot (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$

In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten:

$$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$

Daraus folgt: Man benötigt bereits für eine DFT (oder eine IDFT) mit $N = 1000$ knapp acht Millionen Rechenoperationen. Für $N =16 $ sind immerhin noch 1920 Rechenoperationen erforderlich.

Ist der Parameter $N$ eine Potenz zur Basis 2, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem Sammelbegriff Fast–Fouriertransformation – abgekürzt FFT – zusammengefasst. Alle diese Methoden basieren auf dem Überlagerungssatz der DFT.

Überlagerungssatz der DFT

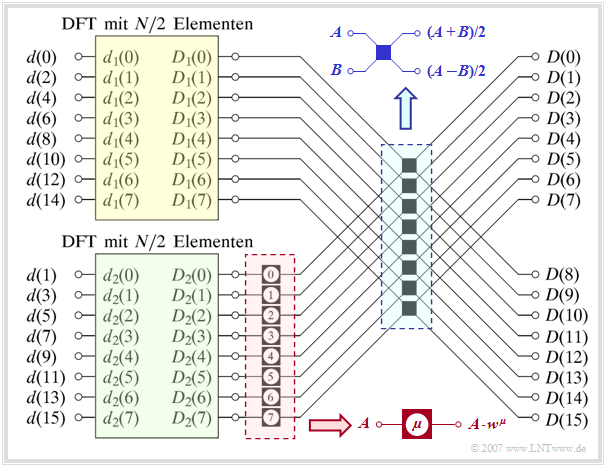
Die Grafik verdeutlicht den so genannten Überlagerungssatz der DFT am Beispiel $N = 16$.

Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet:

Die Folge $\langle d(\nu)\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle d_1(\nu)\rangle$ und $\langle d_2(\nu)\rangle$ jeweils halber Länge separiert (gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente

$$d_1(\nu) = d(2\nu), \hspace{0.2cm}d_2(\nu) = d(2\nu+1) \hspace{0.05cm}.$$

Die Ausgangsfolgen $\langle D_1(\mu )\rangle$ und $\langle D_2(\mu )\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$:

$$\langle D_1(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle d_1(\nu) \rangle , \hspace{0.2cm} \langle D_2(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle d_2(\nu) \rangle \hspace{0.05cm}.$$

Die Ausgangswerte $\langle D_2(\mu )\rangle$ der unteren (grünen) DFT (mit $0 \le \mu \lt N/2$) werden danach im rot umrandeten Block durch komplexe Drehfaktoren hinsichtlich Phasenlage verändert:

$$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$

Jeder einzelne Butterfly im blau umrandeten Block liefert durch Addition bzw. Subtraktion zwei Elemente der gesuchten Ausgangsfolge. Mit $0 \le \mu \lt N/2$ gilt dabei:

$$\begin{align*}D(\mu) & = {1}/{2}\cdot \left[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\right],\\ D(\mu +{N}/{2}) & = {1}/{2}\cdot \left[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\right]\hspace{0.05cm}.\end{align*}$$

Durch diese erste Anwendung des Überlagerungssatzes halbiert sich somit in etwa der Rechenaufwand.

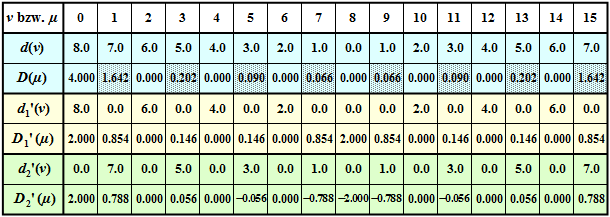
Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der Zeile 2 der folgenden Tabelle „dreieckförmig” belegt. Beachten Sie hierbei die periodische Fortsetzung der DFT, so dass der lineare Anstieg für $t \lt 0$ durch die Koeffizienten $d(9) ... d(15)$ ausgedrückt wird.

Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der ebenfalls blau hinterlegten Zeile 3 angegebenen Spektralkoeffizienten $D(\mu )$, die bei Vernachlässigung des Aliasingfehlers gleich $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$ wären. Man erkennt, dass sich der Aliasingfehler nur auf die ungeradzahligen Koeffizienten auswirkt (schraffierte Felder). Beispielsweise müsste $D$(1) = 16/ $\pi^2 \approx$ 1.621 $\neq$ 1.642 sein.

Spaltet man die Gesamtfolge $\langle d(\nu)\rangle$ in zwei Teilfolgen $\langle {d_1}'(\nu)\rangle$ und $\langle {d_2}'(\nu)\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten ($\nu = 0, 2, ... , N–2$) und die zweite (grün hinterlegt) nur ungeradzahlige Koeffizienten ($\nu = 1, 3, ... , N–1$) beinhalten und alle anderen zu 0 gesetzt sind, so erhält man die zugehörigen Folgen im Spektralbereich:

$$ \langle {D_1}'(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle {d_1}'(\nu) \rangle , \hspace{0.2cm} \langle {D_2}'(\mu) \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle {d_2}'(\nu) \rangle \hspace{0.05cm}.$$

In den gelb bzw. grün hinterlegten Zeilen $4 ... 7$ erkennt man:

Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch $D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu )$. Dies lässt sich zum Beispiel mit dem Additionstheorem linearer Systeme begründen.
Die Periode der Folge $\langle {D_1}'(\mu )\rangle$ beträgt aufgrund des Nullsetzens eines jeden zweiten Zeitkoeffizienten nun $N/2$ im Gegensatz zur Periode $N$ der Ursprungsfolge $\langle D(\mu )\rangle$:

$${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$

$\langle {D_2}'(\mu )\rangle$ beinhaltet zusätzlich einen Phasenfaktor (Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt:

$${D_2}'(\mu + {N}/{2}) =-{D_2}'(\mu)\hspace{0.05cm}.$$

Die Berechnung von $\langle {D_1}'(\mu )\rangle$ und $\langle {D_2}'(\mu )\rangle$ ist aber jeweils ebenso aufwändig wie die Bestimmung von $\langle D(\mu )\rangle$ , da $\langle {d_1}'(\nu)\rangle$ und $\langle {d_2}'(\nu)\rangle$ ebenfalls aus $N$ Elementen bestehen, auch wenn einige 0 sind.

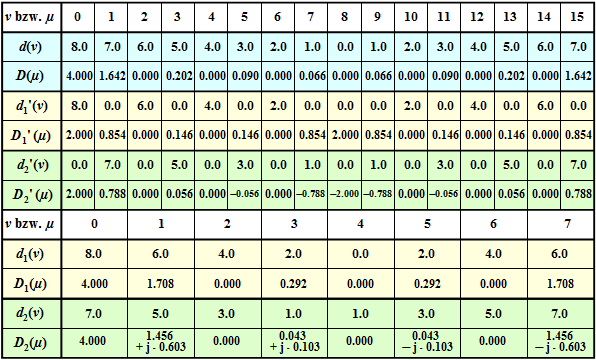
Verzichtet man auf die Koeffizienten ${d_1}'(\nu)$ = 0 mit ungeraden sowie auf ${d_2}'(\nu)$ = 0 mit geraden Indizes, so kommt man zu den Teilfolgen $\langle d_1(\nu)\rangle$ und $\langle d_2(\nu)\rangle$ ⇒ Zeilen 9 und 11. Man erkennt:

Die beiden Zeitfolgen 〈d1(\nu)〉 und 〈d2(\nu)〉 weisen damit ebenso wie die dazugehörigen Spektralfolgen 〈D1(μ)〉 und 〈D2(μ)〉 nur noch die Dimension $N/2$ auf.
Ein Vergleich der Zeilen 5, 7, 10 und 12 zeigt für $0 \le \mu$ \lt N/2$ folgenden Zusammenhang: :'"`UNIQ-MathJax15-QINU`"' *Entsprechend erhält man für $N/2 \le \mu$ \lt N$:

$$\begin{align*}{D_1}'(\mu) \hspace{-0.2cm} & = \hspace{-0.2cm}{1}/{2}\cdot {D_1}(\mu-{N}/{2}),\\ {D_2}'(\mu) \hspace{-0.2cm}& = \hspace{-0.2cm}{1}/{2}\cdot {D_2}(\mu-{N}/{2})\cdot w^{\hspace{0.04cm}\mu} =-{1}/{2}\cdot {D_2}(\mu-{N}/{2})\cdot w^{\hspace{0.04cm}\mu- N/2}\hspace{0.05cm}.\end{align*}$$

Zum Beispiel erhält man mit $N$ = 16 ⇒ $w$ = exp(–j $\cdot \pi$/8) für die Indizes $\mu$ = 1 bzw. $\mu$ = 9:

$${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.2cm} {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = 0.788$$ $$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$ $${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.15cm} {D_2}'(9) =-{1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = -0.788$$ $$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$

Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand. Statt $\mathcal{O}$ = 1920 benötigt man nur $\mathcal{O}$ = 2 · 448 + 8 · (4+2) + 16 · 2 = 976 reelle Operationen. Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N$/2 = 8, der Rest die acht komplexen Multiplikationen und die 16 komplexen Additionen bzw. Subtraktionen.

Radix-2-Algorithmus nach Cooley und Tukey

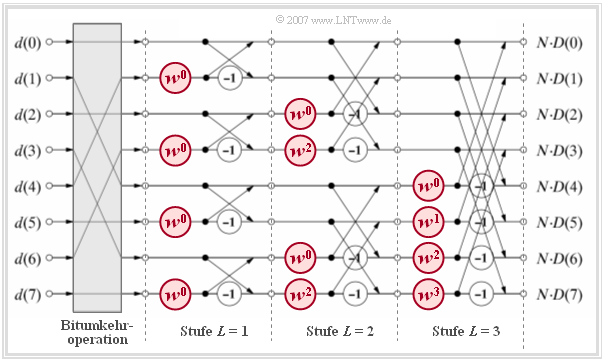
Ebenso wie andere FFT–Algorithmen baut das hier vorgestellte Verfahren von Cooley und Tukey auf dem Überlagerungssatz der DFT auf. Es funktioniert nur dann, wenn die Stützstellenzahl $N$ eine Zweierpotenz ist. Das folgende Bild verdeutlicht den Algorithmus – siehe auch [CT65] – für das Beispiel $N$ = 8, wobei die Transformation vom Zeit– in den Frequenzbereich dargestellt ist.

Vor dem eigentlichen FFT-Algorithmus müssen die Eingangswerte $d$(0), ... , $d$( $N$–1) im grauen Block Bitumkehroperation umsortiert werden. Weiter erkennt man aus obiger Darstellung:

Die Berechnung erfolgt in $\text{log}_2 N$ = 3 Stufen, wobei in jeder Stufe genau $N$/2 = 4 prinzipiell gleiche Berechnungen mit unterschiedlichem $\mu$ (= Exponent des komplexen Drehfaktors) ausgeführt werden. Eine solche Basisoperation bezeichnet man auch als Butterfly.
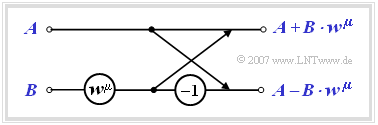
Jeder Butterfly berechnet aus zwei (im Allgemeinen komplexen) Eingangsgrößen $A$ und $B$ die beiden Ausgangsgrößen $A + B \cdot w\mu$ sowie $A – B \cdot w\mu$ entsprechend folgender Skizze:

Die komplexen Spektralkoeffizienten $D$(0), ... , $D$( $N$–1) erhält man am Ausgang der letzten Stufe nach Division durch $N$. Wie in Aufgabe Z5.5 gezeigt wird, ergibt sich gegenüber der DFT eine deutlich kürzere Rechenzeit – z.B. für $N$ = 1024 um mehr als den Faktor 150.

Die inverse DFT zur Berechnung der Zeitkoeffizienten aus den Spektralkoeffizienten lässt sich mit dem gleichen Algorithmus und nur geringfügigen Modifizierungen bewerkstelligen.

Nachfolgend sehen Sie das C–Programm fft(N, Re, Im) gemäß dem oben beschriebenen Radix–2–Algorithmus:

Beim Aufruf beinhalten die beiden Float–Arrays „Re” und „Im” die jeweils $N$ Real– und Imaginärteile der komplexen Zeitkoeffizienten $d$(0), ... , $d$( $N$ – 1).
In den gleichen Feldern „Re” und „Im” werden die N komplexen Spektralkoeffizienten $D$(0), ... , $D$( $N$–1) am Programmende an das aufrufende Programm zurückgegeben.
Aufgrund dieser „In–Place”–Programmierung reichen für diesen Algorithmus $N$ komplexe Speicherplätze aus, allerdings nur, wenn zu Beginn die Eingangswerte umsortiert werden.
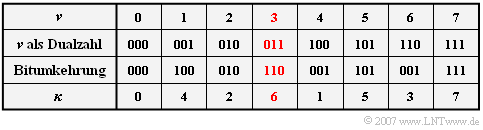
Dies geschieht durch das Programm „bitumkehr”, wobei die Inhalte von Re( $\nu$) und Im( $\nu$) in die Elemente Re( $\kappa$) und Im( $\kappa$) eingetragen werden. Die folgende Tabelle gilt für $N$ = 8.

Schreibt man den Index $\nu$ als Dualzahl und stellt die $\text{log}_2 N$ Bits in umgekehrter Reihenfolge dar, so ergibt sich der neue Index $\kappa$. Beispielsweise wird so aus $\nu$ = 3 der neue Index $\kappa$ = 6.

Aufgabe zum Kapitel

A5.5 Fast-Fouriertransformation