Aufgabe 2.2: Kraftsche Ungleichung

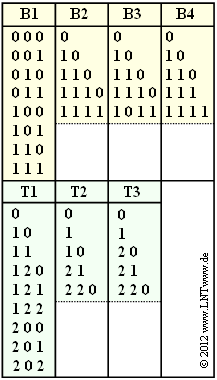
Vier Beispiele für Binärcodes und dazu drei Ternärcodes

In der Abbildung sind einige beispielhafte Binär– und Ternärcodes angegeben.

Beim Binärcode $\rm B1$ werden alle möglichen Quellensymbole $q_\mu$ $($mit Laufindex $\mu = 1$, ... , $8)$ durch jeweils eine Codesymbolfolge $\langle c_\mu \rangle $ einheitlicher Länge $L_\mu = 3$ dargestellt.
Dieser Code ist aus diesem Grund zur Datenkomprimierung ungeeignet.

Die Möglichkeit zur Datenkomprimierung ergibt sich erst dann, wenn

die $M$ Quellensymbole nicht gleichwahrscheinlich, und
die Länge $L_\mu$ der Codeworte unterschiedlich sind.

Diese Eigenschaft weist zum Beispiel der Binärcode $\rm B2$ auf:

Je ein Codewort hat hier die Länge $1$, $2$ bzw. $3$ $(N_1 = 1,\ N_2 = 2,\ N_3 = 3)$.
Zwei Codeworte haben die Länge $L_\mu = 4$ $(N_4 = N_5 = 4)$.

Voraussetzung für die Decodierbarkeit eines solchen Codes ist, dass der Code präfixfrei ist.

Das heißt, dass kein Codewort der Präfix (also der Beginn) eines längeren Codewortes sein darf.

Eine notwendige Bedingung dafür, dass ein Code zur Datenkomprimierung präfixfrei sein kann, wurde 1949 von Leon Kraft angegeben, die so genannte Kraftsche Ungleichung:

$$\sum_{\mu=1}^{M} \hspace{0.2cm} D^{-L_{\mu}} \le 1 \hspace{0.05cm}.$$

Hierbei bezeichnen

$M$ die Anzahl der möglichen Quellensymbole $q_\mu$ ⇒ „Symbolumfang”,
$L_\mu$ die Länge des zum Quellensymbol $q_\mu$ gehörigen Codewortes $c_\mu$,
$D = 2$ kennzeichnet einen Binärcode $(\rm 0$ oder $\rm 1)$ und $D = 3$ einen Ternärcode $(\rm 0$, $\rm 1$, $\rm 2)$.

Ein Code kann nur dann präfixfrei sein, wenn die Kraftsche Ungleichung erfüllt ist.
Die Umkehrung gilt nicht: Wird die Kraftsche Ungleichung erfüllt, so bedeutet das noch lange nicht, dass dieser Code tatsächlich präfixfrei ist.

Hinweis:

Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung der Quellencodierung.

Fragebogen

Musterlösung

(1) Richtig sind die Lösungsvorschläge 1, 2 und 3. Für die angegebenen Binärcodes gilt:

$\rm B1$: $8 \cdot 2^{-3} = 1$ ⇒ Bedingung erfüllt,
$\rm B2$: $1 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3} + 2 \cdot 2^{-4}= 1$ ⇒ Bedingung erfüllt,
$\rm B3$: $1 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3} + 2 \cdot 2^{-4}= 1$ ⇒ Bedingung erfüllt,
$\rm B4$: $1 \cdot 2^{-1} + 1 \cdot 2^{-2} + 2 \cdot 2^{-3} + 1 \cdot 2^{-4}= 17/16$ ⇒ Bedingung nicht erfüllt.

(2) Richtig sind die Lösungsvorschläge 1 und 2:

Der Code $\rm B4$, der die Kraftsche Ungleichung nicht erfüllt, ist mit Sicherheit auch nicht präfixfrei.
Aber bei Erfüllung der Kraftschen Ungleichung ist noch nicht sicher, dass dieser Code auch präfixfrei ist.
Beim Code $\rm B3$ ist „10” der Beginn des Codewortes „1011”.
Dagegen sind die Codes $\rm B1$ und $\rm B2$ tatsächlich präfixfrei.

(3) Richtig sind die Antworten 1 und 3:

Die Kraftsche Ungleichung wird von allen drei Codes erfüllt.
Wie aus der Tabelle hervorgeht, sind die Codes $\rm T1$ und $\rm T3$ tatsächlich präfixfrei.
Der Code $\rm T2$ ist dagegen nicht präfixfrei, da „1” der Beginn des Codewortes „10” ist.

(4) $N_i$ gibt an, wieviele Codeworte mit $i$ Symbolen es im Code gibt. Für den Code $\rm T1$ gilt:

$$N_1 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}, \hspace{0.2cm}N_2 \hspace{0.15cm}\underline{= 2}\hspace{0.05cm}, \hspace{0.2cm}N_3 \hspace{0.15cm}\underline{= 6}\hspace{0.05cm}.$$

(5) Nach der Kraftschen Ungleichung muss gelten

$$N_1 \cdot 3^{-1} + N_2 \cdot 3^{-2} + N_3 \cdot 3^{-3 } \le 1\hspace{0.05cm}.$$

Bei gegebenem $N_1 = 1$ und $N_2 = 2$ wird dies erfüllt, solange gilt:

$$N_3 \cdot 3^{-3 } \le 1 - 1/3 - 2/9 = 4/9 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}N_3 \le 12 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm \Delta}\,N_3 \hspace{0.15cm}\underline{= 6}\hspace{0.05cm}.$$

Die zusätzlichen Codeworte sind $\rm 210, \,211, \,212, \,220, \,221, \,222$.

(6) Für den Code $\rm T3$ gilt:

$S({\rm T3})= 2 \cdot 3^{-1} + 2 \cdot 3^{-2} + 1 \cdot 3^{-3 } = {25}/{27}\hspace{0.05cm}.$
Wegen $S({\rm T3}) \le 1$ erfüllt der Ternärcode $\rm T3$ die Kraftsche Ungleichung und er ist zudem auch präfixfrei.

Betrachten wir nun die vorgeschlagenen neuen Codes.

Code $\rm T4$ $(N_1 = 2, \ N_2 = 2, \ N_3 = 5)$:

$$S({\rm T4})= S({\rm T3}) + 4 \cdot 3^{-3 } = {29}/{27}\hspace{0.1cm} > \hspace{0.1cm}1\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm T4 \hspace{0.15cm}ist\hspace{0.15cm} ungeeignet}\hspace{0.05cm},$$

Code $\rm T5$ $(N_1 = 2, \ N_2 = 2, \ N_3 = 1, \ N_4 = 4)$:

$$S({\rm T5})= S({\rm T3}) + 4 \cdot 3^{-4 } = {79}/{81}\hspace{0.1cm} < \hspace{0.1cm}1\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm T5 \hspace{0.15cm}ist\hspace{0.15cm} geeignet}\hspace{0.05cm},$$

Code $\rm T6$ $(N_1 = 2, \ N_2 = 2, \ N_3 = 2, \ N_4 = 3)$:

$$S({\rm T6})= S({\rm T3}) + 1 \cdot 3^{-3 } + 3 \cdot 3^{-4 } = \frac{75 + 3 + 3}{81}\hspace{0.1cm} = \hspace{0.1cm}1\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm T6 \hspace{0.15cm}ist\hspace{0.15cm} geeignet}\hspace{0.05cm}.$$

Richtig sind also die zwei letzten Lösungsvorschläge. Beispielsweise lauten die insgesamt $N = 9$ Codeworte des präfixfreien Codes $\rm T6$:

$$\rm 0, \, 1, \, 20, \,21, \,220, \,221, \,2220, \, 2221 , \,2222.$$

	$\rm B1$,
	$\rm B2$,
	$\rm B3$,
	$\rm B4$.

	$\rm B1$,
	$\rm B2$,
	$\rm B3$,
	$\rm B4$.

	Ergänzung um vier dreiwertige Codeworte.
	Ergänzung um vier vierwertige Codeworte.
	Ergänzung um ein dreiwertiges und drei vierwertige Codeworte.

	$\rm T1$,
	$\rm T2$,
	$\rm T3$.