Aufgabe 3.2Z: Laplace und Fourier

Vier kausale Zeitsignale

Die Fourier–Transformation kann man für jedes deterministische Signal $x(t)$ anwenden. Für die Spektralfunktion gilt dann:

$$X(f) = \int_{-\infty}^{ +\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}\hspace{0.05cm} .$$

Bei leistungsbegrenzten Signalen – Kennzeichen: unendlich große Energie – beinhaltet $X(f)$ auch Distributionen (Diracfunktionen).

Bei allen kausalen Signalen (und nur bei diesen) ist daneben auch die Laplace-Transformation anwendbar:

$$X_{\rm L}(p) = \int_{0}^{ \infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}\hspace{0.05cm} .$$

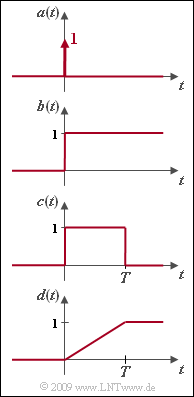
In der Grafik sehen Sie verschiedene kausale Zeitfunktionen, die in dieser Aufgabe behandelt werden:

die Diracfunktion $a(t)$,

die Sprungfunktion $b(t)$,

die Rechteckfunktion $c(t)$,

die Rampenfunktion $d(t)$.

Die Gesetzmäßigkeiten der Fourier–Transformation gelten meist (allerdings nicht immer) auch für die Laplace–Transformation, wobei $p ={\rm j} \cdot 2 \pi f$ zu setzen ist:

Zum Beispiel lautet der Verschiebungssatz in Laplace– bzw. Fourier–Darstellung:

$$x(t- \tau) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\hspace{-0.05cm}\bullet\quad X_{\rm L}(p)\cdot {\rm e}^{-p \hspace{0.05cm} \cdot \hspace{0.05cm}\tau}\hspace{0.05cm} ,$$

$$x(t- \tau) \quad \circ\!\!-\!\!\!-^{\hspace{-0.05cm}}\!\!\!-\!\!\hspace{-0.05cm}\bullet\quad X(f)\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2\pi f \hspace{0.05cm} \cdot \hspace{0.05cm}\tau}\hspace{0.05cm} .$$

Dagegen ergeben sich beim Integrationssatz Unterschiede:

$$\int {x(\tau)} \hspace{0.1cm}{\rm d}\tau \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\hspace{-0.05cm}\bullet\quad X_{\rm L}(p)\cdot \frac{1}{p}\hspace{0.05cm} ,$$

$$\int {x(\tau)} \hspace{0.1cm}{\rm d}\tau \quad \circ\!\!-\!\!\!-^{\hspace{-0.05cm}}\!\!\!-\!\!\hspace{-0.05cm}\bullet\quad X(f)\cdot \left [ {1}/{2} \cdot{\rm \delta } (f) + \frac{1}{{\rm j} \cdot 2\pi f} \right ] \hspace{0.05cm} .$$

Hinweise:

Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.
Das Lernvideo Gesetzmäßigkeiten der Fouriertransformation könnte hilfreich sein .

Fragebogen

Musterlösung

(1) Richtig sind die Lösungsvorschläge 1 und 3:

Berücksichtigt man, dass die Diracfunktion nur bei $t= 0$ ungleich Null ist und das Integral über den Dirac den Wert $1$ liefert, solange das Integrationsintervall den Zeitpunkt $t= 0$ einschließt, so erhält man:

$$A(f) = 1, \hspace{0.2cm}A_{\rm L}(p) = 1 \hspace{0.05cm} .$$

(2) Richtig sind wieder die Lösungsvorschläge 1 und 3:

Die Sprungfunktion $b(t) = \gamma(t)$ ist das Integral über die Diracfunktion $a(t) = \delta(t)$ ⇒ man kann den Integrationssatz anwenden:

$$b(t) = \int_{-\infty}^t {a(\tau)} \hspace{0.1cm}{\rm d}\tau \hspace{0.3cm}\Rightarrow \hspace{0.3cm} B_{\rm L}(p) =A_{\rm L}(p)\cdot {1}/{p} = {1}/{p}\hspace{0.05cm} ,$$

$$B(f) = A(f)\cdot \left [ {1}/{2} \cdot{\rm \delta } (f) + \frac{1}{{\rm j} \cdot 2\pi f} \right ] = {1}/{2} \cdot{\rm \delta } (f) + \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm} .$$

(3) Richtig sind die Lösungsvorschläge 2 und 3:

Nachdem die (kausale) Rechteckfunktion als Differenz zweier Sprungfunktionen dargestellt werden kann, erhält man mit dem Verschiebungssatz:

$$c(t)= b(t) - b(t-T) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C_{\rm L}(p) =B_{\rm L}(p)- B_{\rm L}(p) \cdot {\rm e}^{-p \hspace{0.05cm} \cdot \hspace{0.05cm}T} = {1}/{p} \cdot \big [ 1- {\rm e}^{-p \hspace{0.05cm} \cdot \hspace{0.05cm}T} \big ] \hspace{0.05cm} .$$

Da die Rechteckfunktion eine endliche Energie besitzt, gilt für das Fourierspektrum:

$$C(f) = C_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} = \frac{1}{{\rm j} \cdot 2\pi f} \cdot \big [ 1- {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi f T} \big ] \hspace{0.05cm}.$$

Nach einigen trigonometrischen Umformungen kann hierfür auch geschrieben werden:

$$C(f) = T \cdot {\rm si} (2 \pi f{T})+ {\rm j} \cdot \frac{{\rm cos} (2 \pi f{T})-1}{2\pi f} \hspace{0.05cm}.$$

(4) Richtig ist der Lösungsvorschlag 1, da gilt:

$$d(t) = \frac{1}{T} \cdot \int\limits_{-\infty}^t {c(\tau)} \hspace{0.1cm}{\rm d}\tau \hspace{0.3cm}\Rightarrow \hspace{0.3cm} D_{\rm L}(p) =C_{\rm L}(p)\cdot \frac{1}{p \cdot T} = \frac{1- {\rm e}^{-p \hspace{0.05cm}\cdot \hspace{0.05cm}T}}{p^2 \cdot T}\hspace{0.05cm} .$$

Da sich $d(t)$ bis ins Unendliche erstreckt, ist der einfache Zusammenhang zwischen $D_{\rm L}(p)$ und $D(f)$ gemäß Lösungsvorschlag 3 nicht gegeben.
$D(f)$ beinhaltet vielmehr auch eine Diracfunktion bei der Frequenz $f = 0$.

	$B_{\rm L}(p) = 1/p$.
	$B(f) = 1/({\rm j} \cdot 2 \pi f)$
	$B(f) = 1/2 \cdot \delta(f) - {\rm j}/(2 \pi f)$.

	$C_{\rm L}(p) = {\rm si}(pT)$.
	$C_{\rm L}(p) = \big [1-{\rm e}^{-p\hspace{0.05cm} \cdot \hspace{0.05cm}T} \big ]/p$.
	$C(f) = C_{\rm L}(p)$ mit $p = 2 \pi f$.

	$D_{\rm L}(p) = \big[1-{\rm e}^{-p\hspace{0.05cm} \cdot \hspace{0.05cm}T}\big]/(p^2T)$.
	$D_{\rm L}(p) = 1-{\rm e}^{-p\hspace{0.05cm} \cdot \hspace{0.05cm}T}$.
	$D(f) = D_{\rm L}(p)$ mit $p = 2 \pi f$.

	$A_{\rm L}(p) = 1$.
	$A(f) = \delta(f)$.
	$A(f) = 1$.