Inhaltsverzeichnis
Einige allgemeine Bemerkungen zu AKF und LDS
Zur Beschreibung der inneren statistischen Bindungen zwischen den benachbarten Signalwerten $r(t)$ und $r(t+ \Delta t)$ eignet sich die Autokorrelationsfunktion $\rm (AKF)$:
- \[\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\big [ r(t) \cdot r^{\star}(t + {\rm \Delta}t)\big ] \hspace{0.05cm}.\]
Gegenüber der Definition unter obigem Link sind folgende Unterschiede zu erkennen:
- Die AKF–Variable ist hier mit $\Delta t$ anstelle von $\tau$ bezeichnet, da wir in diesem Buch das „$\tau$” noch für die 2D–Impulsantwort $h(t, \hspace{0.05cm}\tau)$ benötigen.
- Das äquivalente Tiefpass–Signal $r(t)$ ist komplex. Durch den Faktor $1/2$ bezieht sich aber die AKF $\varphi_r ({\rm \Delta}t)$ und insbesondere die Leistung $\varphi_r ({\rm \Delta}t = 0)$ auf das (reelle) Bandpass–Signal $r_{\rm BP}(t)$.
Beim Rayleigh–Fading–Kanalmodell gilt $r(t) = s(t) \cdot z(t)$. Damit ergibt sich für dessen AKF:
- \[\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\big [ s(t) \cdot z(t) \cdot s^{\star}(t + {\rm \Delta}t) \cdot z^{\star}(t + {\rm \Delta}t)\big ] = \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)\hspace{0.05cm}.\]
Für die AKF von Sendesignal $s(t)$ und multiplikativem Faktor $z(t)$ gelten folgende Definitionen:
- \[ \varphi_s ({\rm \Delta}t)= {1}/{2} \cdot {\rm E}\big [ s(t) \cdot s^{\star}(t + {\rm \Delta}t)\big ] \hspace{0.05cm},\]
- \[\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]\hspace{0.05cm}.\]
- Der Faktor $1/2$ ist nur bei der AKF–Berechnung von Bandpass–Signalen im äquivalenten Tiefpass–Bereich zu berücksichtigen, nicht jedoch bei $\varphi_z ({\rm \Delta}t)$. Ansonsten würde sich $\varphi_r ({\rm \Delta}t) \ne \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)$ ergeben.
Aufgrund der Definition $\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ]$ ist die AKF auch bei einer komplexen Zeitfunktion $z(t)$ stets reell und zudem bezüglich $ {\rm \Delta}t$ gerade. Berücksichtigen wir weiterhin, dass
- $z(t) = x(t) + {\rm j} \cdot y(t) $ ist,
- $x(t)$ und $y(t)$ gleiche statistische Eigenschaften aufweisen, und
- es zwischen $x(t)$ und $y(t)$ keine statistischen Bindungen gibt,
so lässt sich für die AKF des komplexen Faktors $z(t)$ schreiben:
- \[\varphi_z ({\rm \Delta}t) = \varphi_x ({\rm \Delta}t) + \varphi_y ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t) \hspace{0.05cm}.\]
$\text{Fazit:}$ Daraus ergibt sich folgende Vereinfachung:
- Zur Ermittlung der statistischen Bindungen der komplexen Größe $z(t)$ muss nur einer der beiden Gaußprozesse betrachtet werden. Im Folgenden sei dies $x(t)$.
- Wir berechnen zuerst die Autokorrelationsfunktion $\rm (AKF)$ $\varphi_x ({\rm \Delta}t) = {\rm E}\big[x(t) \cdot x(t + {\rm \Delta}t)\big]$ des Realteils und danach dessen Leistungsdichtespektrum $\rm (LDS)$
- \[{\it \Phi}_x (f_{\rm D}) = \int_{-\infty}^{+\infty} \varphi_x ({\rm \Delta}t) \cdot {\rm e}^{ -- {\rm j \cdot 2 \pi} \cdot f_{\rm D} \cdot {\rm \Delta}t } \hspace{0.15cm}{\rm d}( {\rm \Delta}t) \hspace{0.3cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.3cm} \varphi_x ({\rm \Delta}t) \hspace{0.05cm}. \]
- Für die entsprechenden Kenngrößen des komplexen Zufallsprozesses $z(t)$ gilt dann:
- \[\varphi_z ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t)\hspace{0.05cm},\hspace{0.2cm} {\it \Phi}_z (f_{\rm D}) = 2 \cdot {\it \Phi}_x (f_{\rm D}) \hspace{0.05cm}.\]
- Die $\rm LDS$–Variable ist die Dopplerfrequenz $f_{\rm D}$, da beim Mobilfunk der so genannte „Dopplereffekt” die Ursache der statistischen Bindungen ist.
Dieser Effekt wird auf der nächsten Seite genauer erläutert.
Phänomenologische Beschreibung des Dopplereffekts
Die statistischen Bindungen innerhalb der reellen „Signale” $x(t)$ und $y(t)$ bzw. innerhalb der komplexen Größe $z(t)$ sind auf den Dopplereffekt zurückzuführen. Dieser wurde Mitte des 19. Jahrhunderts von dem österreichischen Mathematiker, Physiker und Astronomen Christian Andreas Doppler theoretisch vorhergesagt und nach ihm benannt.
$\text{Definition:}$ Als Dopplereffekt bezeichnet man die Veränderung der wahrgenommenen Frequenz von Wellen jeder Art, die sich dann ergibt, wenn sich Quelle (Sender) und Beobachter (Empfänger) relativ zueinander bewegen.
Qualitativ lässt sich der Dopplerreffekt wie folgt beschreiben:
- Nähern sich Beobachter und Quelle einander an, so erhöht sich aus Sicht des Beobachters die Frequenz, egal, ob sich der Beobachter bewegt oder die Quelle oder beide.
- Entfernt sich die Quelle vom Beobachter oder der Beobachter von der Quelle, so nimmt der Beobachter eine niedrigere Frequenz wahr, als tatsächlich gesendet wurde.
$\text{Beispiel 1:}$ Wir betrachten die Tonhöhenänderung des „Martinhorns” eines Rettungswagens. Solange sich das Fahrzeug annähert, hört der Beobachter einen höheren Ton als bei stehendem Wagen. Entfernt sich der Rettungswagen, so wird ein tieferer Ton wahrgenommen.
Den gleichen Effekt stellt man auch bei einem Autorennen fest. Die Frequenzänderungen und der „Sound” sind dabei um so deutlicher, je schneller die Autos fahren.
Den Sachverhalt kann man sich in diesem Lerntutorial mit dem interaktiven Applet Zur Verdeutlichung des Dopplereffekts verdeutlichen.
$\text{Beispiel 2:}$
Einige Eigenschaften dieses noch aus dem Physikunterricht bekannten Effekts sollen nun anhand von Bildschirmabzügen einer früheren Version der oben genannter Animation dargestellt werden, wobei natürlich die dynamischen Programmeigenschaften verloren gehen.
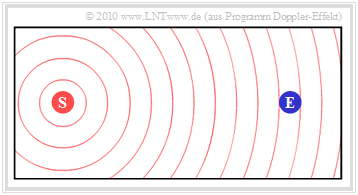
Die erste Grafik zeigt die Ausgangssituation:
- Der ruhende Sender $\rm (S)$ gibt die konstante Frequenz $f_{\rm S}$ ab.
- Die Wellenausbreitung ist in der Grafik durch konzentrische Kreise um $\rm (S)$ veranschaulicht.
- Beim ebenfalls ruhenden Empfänger $\rm (E)$ kommt dann natürlich die Frequenz $f_{\rm E} = f_{\rm S}$ an.
$\text{Beispiel 3:}$ Der nächste Schnappschuss zeigt den Fall, dass sich der Sender $\rm (S)$ mit konstanter Geschwindigkeit $v$ von seinem Startpunkt $\rm (S_0)$ auf den Empfänger $\rm (E)$ zu bewegt hat.
- Das rechte Diagramm zeigt, dass die vom Empfänger wahrgenommene Frequenz $f_{\rm E}$ (blaue Schwingung) um etwa $20\%$ größer ist als die Frequenz $f_{\rm S}$ am Sender (rote Schwingung).
- Aufgrund der Bewegung des Senders sind nun die Kreise nicht mehr konzentrisch.
- Das links dargestellte Szenerio ergibt sich, wenn sich der Sender $\rm (S)$ vom Empfänger $\rm (E)$ entfernt: Dann ist die Empfangsfrequenz $f_{\rm E}$ (blaue Schwingung) um etwa $20\%$ kleiner als die Sendefrequenz $f_{\rm S}$.
$\text{Zu berücksichtigen ist allerdings:}$
- Alle diese Angaben gelten für unrealistisch große Geschwindigkeit $(v = c/5)$, wobei $c = 3 \cdot 10^8 \, {\rm m/s}$ die Lichtgeschwindigkeit angibt. Beim Mobilfunk sind die Abweichungen zwischen $f_{\rm S}$ und $f_{\rm E}$ dagegen meist nur ein Bruchteil der Sendefrequenz.
- Die exakte Gleichung für die Empfangsfrequenz $f_{\rm E}$ unter Einbeziehung eines Winkels $\alpha$ zwischen der Bewegungsrichtung und der Verbindungslinie Sender–Empfänger lautet:
- \[f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c \cdot \cos(\alpha)} \hspace{0.05cm}.\]
- Wie in der Aufgabe 1.4Z gezeigt werden soll, kann man bei realistischen Geschwindigkeiten $(v \ll c)$ von der folgenden Näherung ausgehen, bei der die durch die Relativitätstheorie beschriebenen Effekte unberücksichtigt bleiben:
- \[f_{\rm E} \approx f_{\rm S} \cdot \big [1 +{v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.05cm}.\]
Dopplerfrequenz und deren Verteilung
Wir fassen die Aussagen der letzten Seite nochmals kurz zusammen, wobei wir von der zweiten, also der nicht–relativistischen Gleichung ausgehen:
- Bei einer Relativbewegung zwischen Sender (Quelle) und Empfänger (Beobachter) kommt es zu einer Verschiebung um die Dopplerfrequenz $f_{\rm D} = f_{\rm E} - f_{\rm S}$.
- Eine positive Dopplerfrequenz $(f_{\rm E} > f_{\rm S})$ ergibt sich dann, wenn sich Sender und Empfänger (relativ) aufeinander zu bewegen. Eine negative Dopplerfrequenz $(f_{\rm E} < f_{\rm S})$ bedeutet, dass sich Sender und Empfänger (direkt oder unter einem Winkel) voneinander entfernen.
- Die maximale Frequenzverschiebung tritt auf, wenn sich Sender und Empfänger direkt aufeinander zu bewegen ⇒ Winkel $\alpha = 0^\circ$. Dieser Maximalwert hängt in erster Näherung von der Sendefrequenz $ f_{\rm S}$ und der Geschwindigkeit $v$ ab $(c = 3 \cdot 10^8 \, {\rm m/s}$ gibt die Lichtgeschwindigkeit an$)$:
- \[f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.\]
- Erfolgt die Relativbewegung unter einem beliebigen Winkel $\alpha$ zur Verbindungslinie Sender–Empfänger, so entsteht eine Dopplerverschiebung um
- \[f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} - \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \le f_{\rm D} \le + \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{0.05cm}.\]
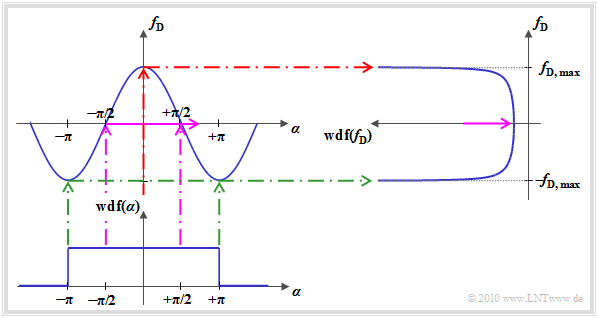
$\text{Fazit:}$ Unter der Annahme gleichwahrscheinlicher Bewegungsrichtungen $($Gleichverteilung für den Winkel $\alpha$ im Bereich $- \pi \le \alpha \le +\pi)$ ergibt sich für die Wahrscheinlichkeitsdichtefunktion $($hier mit „wdf” bezeichnet$)$ der Dopplerfrequenz im Bereich $- f_\text{D, max} \le f_{\rm D} \le + f_\text{D, max}$:
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
Außerhalb des Bereichs zwischen $-f_{\rm D}$ und $+f_{\rm D}$ hat die Wahrscheinlichkeitsdichtefunktion stets den Wert Null.
$\text{Herleitung:}$ Die entstehende Dopplerfrequenz in Abhängigkeit des Bewegungswinkels $\alpha$ lautet:
- \[f_{\rm D} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) = g(\alpha) \hspace{0.05cm}.\]
Wir bezeichnen diese Funktion mit $g(\alpha)$ und gehen davon aus, dass
- $\alpha$ alle Winkelwerte zwischen $\pm \pi$ annimmt,
- und zwar mit gleicher Wahrscheinlichkeit ⇒ Gleichverteilung.
Dann ergibt sich für die Wahrscheinlichkeit der Dopplerfrequenz entsprechend dem Kapitel Transformation von Zufallsgrößen im Buch „Stochastische Signaltheorie”:
- \[{\rm wdf}(f_{\rm D})=\frac{ {\rm wdf}(\alpha)}{\vert g\hspace{0.08cm}'(\alpha)\vert}\Bigg \vert_{\hspace{0.1cm} \alpha=h(f_{\rm D})} \hspace{0.05cm}\]
Verwendet sind hier
- die Ableitung $g\hspace{0.08cm}'(\alpha)= - f_\text{D, max} \cdot \sin(\alpha)$, und
- die Umkehrfunktion $ \alpha = h(f_{\rm D})$.
Im Beispiel lautet die Umkehrfunktion:
- $$ \alpha = \arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}).$$
Die Grafik veranschaulicht den Rechengang zur Bestimmung der Dopplerfrequenz–WDF:
- Da die Kennlinie zwischen der Dopplerfrequenz $f_{\rm D}$ und dem Winkel $\alpha$ ⇒ $ g(\alpha) = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha)$ auf den Wert $f_{\rm D, \hspace{0.05cm} max}$ begrenzt ist, ist für $f_{\rm D}$ kein Wert außerhalb dieses Bereichs möglich.
- Bei der Transformation von Zufallsgrößen muss zwischen Bereichen mit positiver und negativer Steigung der Transformationskennlinie unterschieden werden. Die $\alpha$–Werte zwischen $-\pi$ und $0$ $($positive Steigung der Transformationskennlinie$)$zwischen der Dopplerfrequenz $f_{\rm D}$ und dem Winkel $\alpha$ liefern das Ergebnis
- \[{\rm wdf}(f_{\rm D})=\frac{1/(2\pi)}{f_{\rm D, \hspace{0.05cm} max} \cdot \sin(\alpha)} \Bigg \vert_{\hspace{0.1cm} \alpha=\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})} = \frac{(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} )^{-1} }{ \sin(\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}))} = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- Aus Symmetriegründen trägt der positive $\alpha$–Bereich in gleicher Weise bei, so dass im inneren Bereich insgesamt gilt:
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- Winkel im Bereich um $\alpha = \pm \pi/2$ führen zu einer kleinen Dopplerfrequenz ⇒ $f_{\rm D} \approx 0$ $($violette Markierung$)$. Aufgrund der relativ großen Steigung der cosinusförmigen Kennlinie $g(\alpha)$ bei $\alpha = \pm \pi/2$ ist der WDF–Wert bei $f_{\rm D} \approx 0$ allerdings sehr klein.
- Kleine Winkel $($um $\alpha \approx 0)$ führen dagegen zur maximalen Dopplerfrequenz ⇒ $f_{\rm D} \approx f_{\rm D, \hspace{0.05cm} max}$ $($rote Markierung$)$. Aufgrund der nahezu horizontalen Kennlinie $g(\alpha)$ ist hier die $f_{\rm D}$–WDF deutlich größer. Für $f_{\rm D} \equiv f_{\rm D, \hspace{0.05cm} max}$ ergibt sich sogar ein unendlich großer Wert.
- Winkel um $\alpha = \pm \pi$ führen dagegen zur Dopplerfrequenz $f_{\rm D} \approx -f_{\rm D, \hspace{0.05cm} max}$ $($grüne Markierung$)$. Auch hier ist die Kennlinie nahezu horizontal und es ergibt sich wiederum ein großer WDF–Wert.
AKF und LDS bei Rayleigh–Fading
Wir setzen nun eine in alle Richtungen gleich abstrahlende Antenne voraus. Dann ist das Doppler–LDS formgleich mit der WDF der Dopplerfrequenzen.
Für ${\it \Phi}_x(f_{\rm D})$ muss die WDF noch mit der Leistung $\sigma^2$ des Gaußprozesses multipliziert werden, und für das resultierende LDS ${\it \Phi}_z(f_{\rm D})$ des komplexen Faktors $z(t) = x(t) + {\rm j} \cdot y(t) $ gilt nach Verdoppelung:
- \[{\it \Phi}_z(f_{\rm D}) = \left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} |f_{\rm D}| \le f_{\rm D, \hspace{0.05cm} max} \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.\]
Man nennt diesen Verlauf nach William C. Jakes Jr. das Jakes–Spektrum. Die Verdoppelung ist notwendig, da bisher nur der Beitrag des Realteils $x(t)$ betrachtet wurde.
Die zugehörige Autokorrelationsfunktion (AKF) erhält man nach Fourierrücktransformation:
- \[\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm},\]
mit der Besselfunktion erster Art und nullter Ordnung (erste Gleichung: Definition, zweite Gleichung: Reihenentwicklung):
- \[{\rm J }_0 (u) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{- {\rm j }\hspace{0.03cm}\cdot \hspace{0.03cm}u \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} = \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(-1)^k \cdot (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
Die Zahlenwerte dieser Funktion erhalten Sie mit dem gleichnamigen Applet.
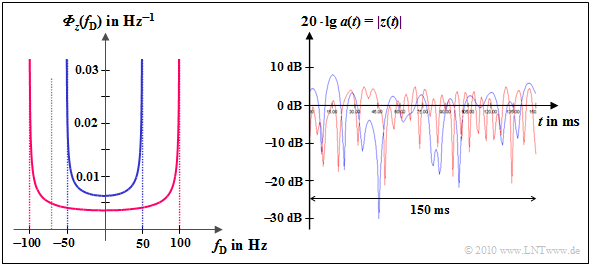
$\text{Beispiel 4:}$ Links dargestellt ist das Jakes–Spektrum
- für $f_{\rm D, \hspace{0.05cm} max} = 50 \ \rm Hz$ (blaue Kurve) bzw.
- für $f_{\rm D, \hspace{0.05cm} max} = 100 \ \rm Hz$ (rote Kurve).
Beim GSM–D–Netz $(f_{\rm S} = 900 \ \rm MHz)$ entsprechen diese Werte den Geschwindigkeiten $v = 60 \ \rm km/h$ bzw. $v = 120 \ \rm km/h$.
Beim E–Netz $(f_{\rm S} = 1.8 \ \rm GHz)$ gelten diese Werte für halb so große Geschwindigkeiten: $v = 30 \ \rm km/h$ bzw. $v = 60 \ \rm km/h$.
Das rechte Bild zeigt den logarithmierten Betrag von $z(t)$:
- Man erkennt das doppelt so schnelle Fading des roten Kurvenverlaufs.
- Die Rayleigh–WDF (Amplitudenverteilung) ist unabhängig von $f_{\rm D, \hspace{0.05cm} max}$ und deshalb für beide Fälle gleich.
Aufgaben zum Kapitel
Aufgabe 1.4: Rayleigh–WDF und Jakes–LDS
Aufgabe 1.4Z: Zum Dopplereffekt
A1.5: Nachbildung des Jakes–Spektrums