Inhaltsverzeichnis
- 1 # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
- 2 Eigenschaften und Beispiele
- 3 Verbundwahrscheinlichkeitsdichtefunktion
- 4 Zweidimensionale Verteilungsfunktion
- 5 WDF und VTF bei statistisch unabhängigen Komponenten
- 6 WDF und VTF bei statistisch abhängigen Komponenten
- 7 Erwartungswerte zweidimensionaler Zufallsgrößen
- 8 Korrelationskoeffizient
- 9 Regressionsgerade
- 10 Aufgaben zum Kapitel
# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
Nun werden Zufallsgrößen mit statistischen Bindungen behandelt und anhand typischer Beispiele verdeutlicht.
Nach der allgemeinen Beschreibung zweidimensionaler Zufallsgrößen wenden wir uns folgenden Beschreibungsgrößen zu:
- der Autokorrelationsfunktion (AKF),
- der Kreuzkorrelationsfunktion (KKF),
- den zugehörigen Spektralfunktionen (Leistungsdichtespektrum, Kreuzleistungsdichtespektrum).
Im Einzelnen werden behandelt:
- die statistische Beschreibung von »2D–Zufallsgrößen« mit Hilfe der Verbund–WDF,
- der Unterschied zwischen »statistischer Abhängigkeit« und »Korrelation«,
- die Klassifizierungsmerkmale »Stationarität« und »Ergodizität« stochastischer Prozesse,
- die Definitionen von »Autokorrelationsfunktion« $\rm (AKF)$ und »Leistungsdichtespektrum« $\rm (LDS)$,
- die Definitionen von »Kreuzkorrelationsfunktion« und »Kreuzleistungsdichtespektrum«,
- die numerische Ermittlung all dieser Größen im zwei– und mehrdimensionalen Fall.
Weitere Informationen zum Thema „Zweidimensionale Zufallsgrößen” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 5: Zweidimensionale Zufallsgrößen (Programm „zwd”)
- Kapitel 9: Stochastische Prozesse (Programm „sto”)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP–Version des Programms,
- der Praktikumsanleitung – Teil A ⇒ Link verweist auf die PDF–Version mit Kapitel 5: Seite 81-97,
- der Praktikumsanleitung – Teil B ⇒ Link verweist auf die PDF–Version mit Kapitel 9: Seite 207-228.
Eigenschaften und Beispiele
Als Überleitung zu den Korrelationsfunktionen betrachten wir nun zwei Zufallsgrößen $x$ und $y$, zwischen denen statistische Abhängigkeiten bestehen.
Jede der beiden Zufallsgrößen kann für sich alleine beschrieben werden mit den eingeführten Kenngrößen
- entsprechend dem zweiten Hauptkapitel ⇒ Diskrete Zufallsgrößen
- bzw. dem dritten Hauptkapitel ⇒ Kontinuierliche Zufallsgrößen.
$\text{Definition:}$ Zur Beschreibung der Wechselbeziehungen zwischen zwei Größen $x$ und $y$ ist es zweckmäßig, die beiden Komponenten zu einer zweidimensionalen Zufallsgröße $(x, y)$ zusammenzufassen.
- Die Einzelkomponenten können Signale sein wie der Real– und Imaginärteil eines phasenmodulierten Signals.
- Aber es gibt auch in anderen Bereichen eine Vielzahl von 2D–Zufallsgrößen, wie das folgende Beispiel zeigen soll.
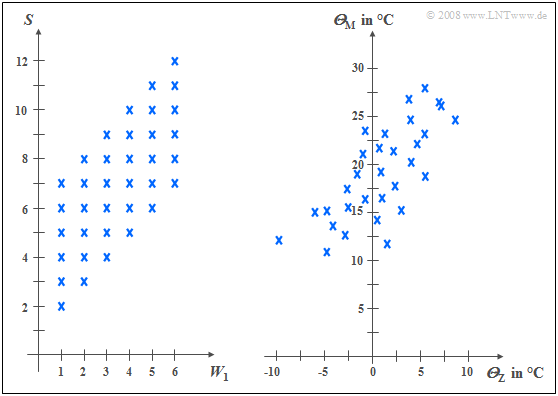
$\text{Beispiel 1:}$ Das linke Diagramm stammt von dem Zufallsexperiment „Werfen mit zwei Würfeln”. Nach rechts aufgetragen ist die Augenzahl des ersten Würfels $(W_1)$, nach oben die Summe $S$ beider Würfel. Die beiden Komponenten sind hier jeweils diskrete Zufallsgrößen, zwischen denen statistische Bindungen bestehen:
- Ist $W_1 = 1$, so kann $S$ nur Werte zwischen $2$ und $7$ annehmen und zwar mit jeweils gleicher Warscheinlichkeit.
- Dagegen sind bei $W_1 = 6$ für $S$ alle Werte zwischen $7$ und $12$ möglich, ebenfalls mit gleicher Warscheinlichkeit.
In der rechten Grafik sind die Maximaltemperaturen der $31$ Tage im Mai 2002 von München (nach oben) und der Zugspitze (nach rechts) gegenübergestellt. Beide Zufallsgrößen sind wertkontinuierlich:
- Obwohl die Messpunkte etwa $\text{100 km}$ auseinander liegen und es auf der Zugspitze aufgrund der unterschiedlichen Höhenlagen $($knapp $3000$ gegenüber $520$ Meter$)$ im Mittel um etwa $20$ Grad kälter ist als in München, erkennt man doch eine gewisse statistische Abhängigkeit zwischen den beiden Zufallsgrößen ${\it Θ}_{\rm M}$ und ${\it Θ}_{\rm Z}$.
- Ist es in München warm, dann sind auch auf der Zugspitze eher angenehme Temperaturen zu erwarten. Der Zusammenhang ist aber nicht deterministisch: Der kälteste Tag im Mai 2002 war in München ein anderer als der kälteste Tag auf der Zugspitze.
Verbundwahrscheinlichkeitsdichtefunktion
Wir beschränken uns hier meist auf kontinuierliche Zufallsgrößen.
- Manchmal wird jedoch auch auf die Besonderheiten zweidimensionaler diskreter Zufallsgrößen genauer eingegangen.
- Die meisten der vorher für eindimensionale Zufallsgrößen definierten Kenngrößen kann man problemlos auf zweidimensionale Größen erweitern.
$\text{Definition:}$ Die Wahrscheinlichkeitsdichtefunktion der zweidimensionalen Zufallsgröße an der Stelle $(x_\mu, y_\mu)$ ⇒ Verbundwahrscheinlichkeitsdichtefunktion ist eine Erweiterung der eindimensionalen WDF $(∩$ kennzeichnet die logische UND-Verknüpfung$)$:
- $$f_{xy}(x_\mu, \hspace{0.1cm}y_\mu) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x_\mu - {\rm \Delta} x/{\rm 2} \le x \le x_\mu + {\rm \Delta} x/{\rm 2}) \cap (y_\mu - {\rm \Delta} y/{\rm 2} \le y \le y_\mu +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$
$\rm Hinweis$:
- Ist die 2D–Zufallsgröße diskret, so muss die Definition geringfügig modifiziert werden:
- Bei den unteren Bereichsgrenzen ist dann gemäß der Seite Verteilungsfunktion bei diskreten Zufallsgrößen das „≤”–Zeichen durch das „<”–Zeichen zu ersetzen.
Anhand dieser (Verbund)–WDF $f_{xy}(x, y)$ werden auch statistische Abhängigkeiten innerhalb der zweidimensionalen Zufallsgröße $(x, y)$ vollständig erfasst im Gegensatz zu den beiden eindimensionalen Dichtefunktionen ⇒ Randwahrscheinlichkeitsdichtefunktionen:
- $$f_{x}(x) = \int _{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}y ,$$
- $$f_{y}(y) = \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x .$$
Diese beiden Randdichtefunktionen $f_x(x)$ und $f_y(y)$
- liefern lediglich statistische Aussagen über die Einzelkomponenten $x$ bzw. $y$,
- nicht jedoch über die Bindungen zwischen diesen.
Zweidimensionale Verteilungsfunktion
$\text{Definition:}$ Die 2D-Verteilungsfunktion ist ebenso wie die 2D-WDF lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF):
- $$F_{xy}(r_{x},r_{y}) = {\rm Pr}\big [(x \le r_{x}) \cap (y \le r_{y}) \big ] .$$
Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der "1D-VTF" und der "2D-VTF":
- Der Funktionalzusammenhang zwischen zweidimensionaler WDF und zweidimensionaler VTF ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt:
- $$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $r_{x}$ und $r_{y}$ angeben:
- $$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$
- Bezüglich der Verteilungsfunktion $F_{xy}(r_{x}, r_{y})$ gelten folgende Grenzwerte:
- $$F_{xy}(-\infty,-\infty) = 0,$$
- $$F_{xy}(r_{\rm x},+\infty)=F_{x}(r_{x} ),$$
- $$F_{xy}(+\infty,r_{y})=F_{y}(r_{y} ) ,$$
- $$F_{xy} (+\infty,+\infty) = 1.$$
- Im Grenzfall $($unendlich große $r_{x}$ und $r_{y})$ ergibt sich demnach für die 2D-VTF der Wert $1$. Daraus erhält man die Normierungsbedingung für die 2D-WDF:
- $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
$\text{Fazit:}$ Beachten Sie den signifikanten Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:
- Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert $1$.
- Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich $1$.
WDF und VTF bei statistisch unabhängigen Komponenten
Bei statistisch unabhängigen Komponenten $x$ und $y$ gilt für die Verbundwahrscheinlichkeit nach den elementaren Gesetzmäßigkeiten der Statistik, falls $x$ und $y$ wertkontinuierlich sind:
- $${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})\big] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$
Hierfür kann bei unabhängigen Komponenten auch geschrieben werden:
- $${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})\big] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{y}(y) \, {\rm d}y.$$
$\text{Definition:}$ Daraus folgt, dass bei statistischer Unabhängigkeit folgende Bedingung bezüglich der 2D–Wahrscheinlichkeitsdichtefunktion erfüllt sein muss:
- $$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$
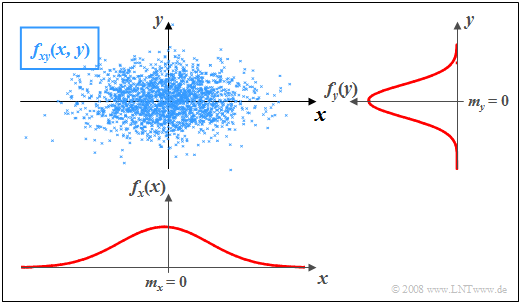
$\text{Beispiel 2:}$ In der Grafik sind die Momentanwerte einer zweidimensionalen Zufallsgröße als Punkte in der $(x, y)$–Ebene eingetragen.
- Bereiche mit vielen Punkten, die dementsprechend dunkel wirken, kennzeichnen große Werte der 2D–WDF $f_{xy}(x, y)$.
- Dagegen besitzt die Zufallsgröße $(x, y)$ in eher hellen Bereichen nur verhältnismäßig wenig Anteile.
Die Grafik kann wie folgt interpretiert werden:
- Die Randwahrscheinlichkeitsdichten $f_{x}(x)$ und $f_{y}(y)$ lassen bereits erkennen, dass sowohl $x$ als auch $y$ gaußähnlich und mittelwertfrei sind, und dass die Zufallsgröße $x$ eine größere Streuung als $y$ aufweist.
- $f_{x}(x)$ und $f_{y}(y)$ liefern jedoch keine Informationen darüber, ob bei der Zufallsgröße $(x, y)$ statistische Bindungen bestehen oder nicht.
- Anhand der 2D-WDF $f_{xy}(x,y)$ erkennt man aber, dass es hier zwischen den beiden Komponenten $x$ und $y$ keine statistischen Bindungen gibt.
- Bei statistischer Unabhängigkeit liefert jeder Schnitt durch $f_{xy}(x, y)$ parallel zur $y$-Achse eine Funktion, die formgleich mit der Rand–WDF $f_{y}(y)$ ist. Ebenso sind alle Schnitte parallel zur $x$-Achse formgleich mit $f_{x}(x)$.
- Diese Tatsache ist gleichbedeutend mit der Aussage, dass in diesem Beispiel $f_{xy}(x, y)$ als Produkt der beiden Randwahrscheinlichkeitsdichten dargestellt werden kann:
- $$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$
WDF und VTF bei statistisch abhängigen Komponenten
Bestehen statistische Bindungen zwischen $x$ und $y$, so liefern unterschiedliche Schnitte parallel zur $x$– bzw. $y$–Achse jeweils unterschiedliche, nicht formgleiche Funktionen. In diesem Fall lässt sich die Verbund–WDF natürlich auch nicht als Produkt der beiden (eindimensionalen) Randwahrscheinlichkeitsdichten beschreiben.
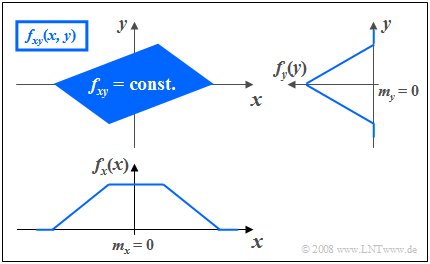
$\text{Beispiel 3:}$ Die Grafik zeigt die Momentanwerte einer zweidimensionalen Zufallsgröße in der $(x, y)$–Ebene, wobei nun im Gegensatz zum $\text{Beispiel 2}$ zwischen $x$ und $y$ statistische Bindungen bestehen.
- Die 2D–Zufallsgröße nimmt im blau eingezeichneten Parallelogramm alle 2D–Werte mit gleicher Wahrscheinlichkeit an.
- Außerhalb des Parallelogramms sind keine Werte möglich.
Man erkennt aus dieser Darstellung:
- Die Integration über $f_{xy}(x, y)$ parallel zur $x$–Achse führt zur dreieckförmigen Randdichte $f_{y}(y)$, die Integration parallel zur $y$–Achse zur trapezförmigen WDF $f_{x}(x)$.
- Aus der 2D-WDF $f_{xy}(x, y)$ ist bereits zu erahnen, dass für jeden $x$–Wert im statistischen Mittel ein anderer $y$–Wert zu erwarten ist.
- Das bedeutet, dass hier die Komponenten $x$ und $y$ statistisch voneinander abhängen.
Erwartungswerte zweidimensionaler Zufallsgrößen
Ein Sonderfall der statistischen Abhängigkeit ist die "Korrelation".
$\text{Definition:}$ Unter Korrelation versteht man eine "lineare Abhängigkeit" zwischen den Einzelkomponenten $x$ und $y$.
- Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
- Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.
Zur quantitativen Erfassung der Korrelation verwendet man verschiedene Erwartungswerte der 2D-Zufallsgröße $(x, y)$.
Diese sind analog definiert zum eindimensionalen Fall
- gemäß Kapitel 2 (bei wertdiskreten Zufallsgrößen)
- bzw. Kapitel 3 (bei wertkontinuierlichen Zufallsgrößen):
$\text{Definition:}$ Für die (nichtzentrierten) Momente gilt die Beziehung:
- $$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$
Die beiden linearen Mittelwerte sind somit $m_x = m_{10}$ und $m_y = m_{01}.$
$\text{Definition:}$ Die auf $m_x$ bzw. $m_y$ bezogenen Zentralmomente lauten:
- $$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$
In dieser allgemein gültigen Definitionsgleichung sind die Varianzen $σ_x^2$ und $σ_y^2$ der zwei Einzelkomponenten durch $\mu_{20}$ bzw. $\mu_{02}$ mit enthalten.
$\text{Definition:}$ Besondere Bedeutung besitzt die Kovarianz $(k = l = 1)$, die ein Maß für die lineare statistische Abhängigkeit zwischen den Zufallsgrößen $x$ und $y$ ist:
- $$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$
Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht.
Anmerkungen:
- Die Kovarianz $\mu_{11}=\mu_{xy}$ hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = {\rm E}\big[x · y\big]$ zusammen:
- $$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$
- Diese Gleichung ist für numerische Auswertungen enorm vorteilhaft, da $m_{xy}$, $m_x$ und $m_y$ aus den Folgen $〈x_v〉$ und $〈y_v〉$ in einem einzigen Durchlauf gefunden werden können.
- Würde man dagegen die Kovarianz $\mu_{xy}$ entsprechend der oberen Definitionsgleichung berechnen, so müsste man in einem ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln und könnte dann erst in einem zweiten Durchlauf den Erwartungswert ${\rm E}\big[(x - m_x) · (y - m_y)\big]$ berechnen.
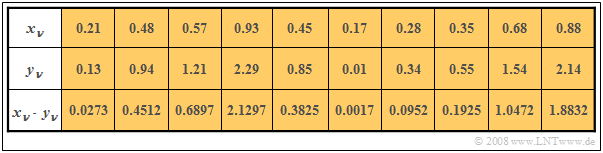
$\text{Beispiel 4:}$ In den beiden ersten Zeilen der Tabelle sind die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$ eingetragen. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben.
- Durch Mittelung über jeweils zehn Folgenelemente erhält man
- $$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$
- Daraus ergibt sich direkt der Wert für die Kovarianz:
- $$\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$$
Ohne Kenntnis der Gleichung $\mu_{xy} = m_{xy} - m_x · m_y$ hätte man zunächst im ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln müssen,
um dann in einem zweiten Durchlauf die Kovarianz $\mu_{xy}$ als Erwartungswert des Produkts der mittelwertfreien Größen bestimmen zu können.
Korrelationskoeffizient
Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} \equiv 0$. Dieser Fall wurde bereits im $\text{Beispiel 2}$ auf der Seite WDF und VTF bei statistisch unabhängigen Komponenten betrachtet.
- Das Ergebnis $\mu_{xy} = 0$ ist aber auch bei statistisch abhängigen Komponenten $x$ und $y$ möglich, nämlich dann, wenn diese unkorreliert, also linear unabhängig sind.
- Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $y=x^2.$
Man spricht von vollständiger Korrelation, wenn die (deterministische) Abhängigkeit zwischen $x$ und $y$ durch die Gleichung $y = K · x$ ausgedrückt wird. Dann ergibt sich für die Kovarianz:
- $\mu_{xy} = σ_x · σ_y$ bei positivem $K$–Wert,
- $\mu_{xy} = - σ_x · σ_y$ bei negativem $K$–Wert.
Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.
$\text{Definition:}$ Der Korrelationskoeffizient ist der Quotient aus der Kovarianz $\mu_{xy}$ und dem Produkt der Effektivwerte $σ_x$ und $σ_y$ der beiden Komponenten:
- $$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$
Der Korrelationskoeffizient $\rho_{xy}$ weist folgende Eigenschaften auf:
- Aufgrund der Normierung gilt stets $-1 \le ρ_{xy} ≤ +1$.
- Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} = 0$.
- Bei strenger linearer Abhängigkeit zwischen $x$ und $y$ ist $ρ_{xy}= ±1$ ⇒ vollständige Korrelation.
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$ mit steigendem $x$ im Mittel kleiner wird.
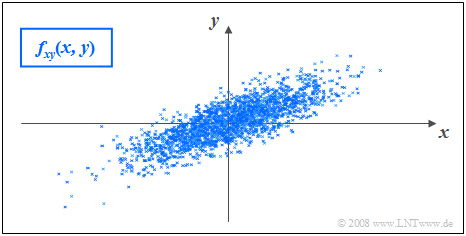
$\text{Beispiel 5:}$ Es gelten folgende Voraussetzungen:
- Die betrachteten Komponenten $x$ und $y$ besitzen jeweils eine gaußförmige WDF.
- Die beiden Streuungen sind unterschiedlich $(σ_y < σ_x)$.
- Der Korrelationskoeffizient beträgt $ρ_{xy} = 0.8$.
Im Unterschied zum Beispiel 2 mit statistisch unabhängigen Komponenten ⇒ $ρ_{xy} = 0$ $($trotz $σ_y < σ_x)$ erkennt man, dass hier bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.
Regressionsgerade
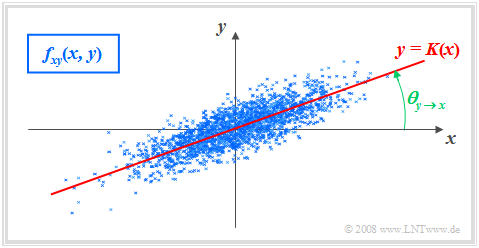
$\text{Definition:}$ Als Regressionsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_x, m_y)$. Manchmal wird diese Gerade auch "Korrelationsgerade" genannt.
Die Regressionsgerade besitzt folgende Eigenschaften:
- Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal:
- $$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$
- Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet:
- $$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$
- Der Winkel, den die Regressionsgerade zur $x$–Achse einnimmt, beträgt:
- $$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$
Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt.
- Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung.
- Das interaktive Applet Korrelation und Regressionsgerade verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird:
- $$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$
Aufgaben zum Kapitel
Aufgabe 4.1: Dreieckiges (x, y)-Gebiet
Aufgabe 4.1Z: Verabredung zum Frühstück
Aufgabe 4.1: Wieder Dreieckgebiet
Aufgabe 4.2Z: Korrelation zwischen $x$ und $e^x$
Aufgabe 4.3: Algebraische und Modulo-Summe
Aufgabe 4.3Z: Diracförmige 2D-WDF