Beschreibungsgrößen digitaler Kanalmodelle

1. Digitalsignalübertragung
2. Digitale Kanalmodelle
3. Beschreibungsgrößen digitaler Kanalmodelle

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

# ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL #

Zum Abschluss dieses Buches werden   Digitale Kanalmodelle  behandelt,

• die das Übertragungsverhalten eines digitalen Übertragungssystems nicht sehr detailliert entsprechend den einzelnen Systemkomponenten beschreiben,

• sondern eher global anhand typischer Fehlerstrukturen.

Solche Kanalmodelle verwendet man vor allem bei  »kaskadierten Übertragungssystemen«  für den inneren Block,  wenn die Leistungsfähigkeit der äußeren Systemkomponenten  – beispielsweise Coder und Decoder –  per Simulation ermittelt werden sollen.

Im Einzelnen werden behandelt:

1. die Beschreibungsgrößen  »Fehlerkorrelationsfunktion«  und   »Fehlerabstandsverteilung«,
2. das  »BSC–Modell«  ("Binary Symmetric Channel")  zur Beschreibung statistisch unabhängiger Fehler,
3. die  »Bündelfehler–Kanalmodelle nach Gilbert–Elliott und McCullough«,
4. das  »Wilhelm–Kanalmodell«  zur formelmäßigen Approximation von gemessenen Fehlerkurven,
5. einige Hinweise zur  »Generierung von Fehlerfolgen«,  zum Beispiel hinsichtlich  »Fehlerabstandssimulation«,
6. die Auswirkungen der verschiedenen Fehlerstrukturen auf  »BMP–Dateien«   ⇒   "Bilder"  und  »WAV–Dateien«   ⇒   "Audios".

Hinweis:   Alle BMP–Bilder und WAV–Audios zu diesem Kapitel

• wurden mit dem Windows–Programm  "Digitale Kanalmodelle & Multimedia"  erzeugt

• aus dem (früheren) Praktikum  "Simulation Digitaler Übertragungssysteme"  am Lehrstuhl für Nachrichtentechnik der TU München.

In diesem Offline–Versuch finden Sie weitere Aufgaben und Simulationen zu den  "Digitalen Kanalmodellen".  Die folgenden Links stellen bereit:

• das Windows-Programm  "DKM"   ⇒   Link verweist auf die ZIP-Version des Programms; und

• die zugehörige  "Praktikumsanleitung"   ⇒   Link verweist auf die PDF-Version.

Anwendung analoger Kanalmodelle

Für Untersuchungen von Nachrichtenübertragungssystemen sind geeignete Kanalmodelle von großer Wichtigkeit,  weil diese

• Voraussetzung für eine Systemsimulation und –optimierung sind, sowie
  

• gleichbleibende und rekonstruierbare Randbedingungen schaffen.
  
  

Für die Digitalsignalübertragung gibt es sowohl analoge als auch digitale Kanalmodelle:

• Ein analoges Kanalmodell muss zwar den Übertragungskanal nicht in allen physikalischen Einzelheiten wiedergeben,  sollte jedoch dessen Übertragungsverhalten inklusive der dominanten Störgrößen funktionell ausreichend genau beschreiben.

• Meist muss ein Kompromiss zwischen mathematischer Handhabbarkeit und dem Bezug zur Realität gefunden werden.
  

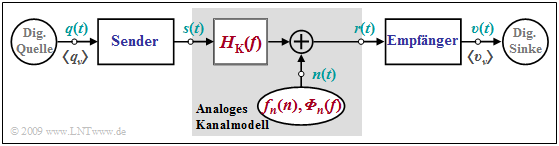
$\text{Beispiel 1:}$  Die Grafik zeigt ein analoges Kanalmodell innerhalb eines digitalen Übertragungssystems. Dieses beinhaltet

• den  "Kanalfrequenzgang"  $H_{\rm K}(f)$  zur Beschreibung der linearen Verzerrungen,  sowie

Analoges Kanalmodell innerhalb eines digitalen Übertragungssystems

• ein additives Störsignal  $n(t)$,  charakterisiert durch
  • die  "Wahrscheinlichkeitsdichtefunktion"  $\rm (WDF)$   ⇒   $f_n(n)$  und
  • das  "Leistungsdichtespektrum"  $\rm (LDS)$   ⇒ ${\it \Phi}_n(f)$.
    

Ein Sonderfall dieses Modells ist der so genannte  "AWGN–Kanal"  ("Additive White Gaussian Noise")  mit den Systemeigenschaften

$$H_{\rm K}(f) = 1\hspace{0.05cm},$$

$${f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm},$$

$${\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm}.$$

Dieses einfache Modell eignet sich zum Beispiel zur Beschreibung eines Funkkanals mit zeitinvariantem Verhalten,  wobei das Modell dahingehend abstrahiert ist,  dass

• der eigentlich bandpassartige Kanal im äquivalenten Tiefpassbereich beschrieben wird,  und
  

• die vom Frequenzband und der Übertragungsweglänge abhängige Dämpfung mit der Varianz  $\sigma^2$  des Rauschsignals  $n(t)$  verrechnet wird.

Zur Berücksichtigung  zeitvarianter Eigenschaften  muss man andere Modelle verwenden,  die im Buch „Mobile Kommunikation” beschrieben werden,  zum Beispiel:

• Das "Rayleigh–Fading",
• das  "Rice–Fading"  und
• das  "Lognormal–Fading" 

Bei  leitungsgebundenen Übertragungssystemen  ist insbesondere der spezifische Frequenzgang des Übertragungsmediums entsprechend den Angaben für

• "Koaxialkabel"  und 
• "Zweidrahtleitung" 

im Buch  "Lineare zeitinvariante Systeme"  zu berücksichtigen,  aber auch,  dass aufgrund von  "Fremdstörungen"  $($Nebensprechen,  elektromagnetische Felder,  usw.$)$  nicht mehr von Weißem Rauschen ausgegangen werden kann.

Bei  optischen Systemen  muss zudem das multiplikativ wirkende,  also signalabhängige  "Schrotrauschen"  geeignet in das analoge Kanalmodell eingearbeitet werden.

Definition digitaler Kanalmodelle

Ein analoges Kanalmodell zeichnet sich durch analoge Eingangs– und Ausgangsgrößen aus.  Dagegen sind bei einem digitalen Kanalmodell  (manchmal auch als  "diskret"  bezeichnet)  sowohl der Eingang als auch der Ausgang zeit– und wertdiskret.

Digitales Kanalmodell und beispielhafte Folgen

Im Folgenden seien dies

• die  "Quellensymbolfolge" $  \langle q_\nu \rangle$  mit  $ q_\nu \in \{\rm L, \ H\}$  und

• die  "Sinkensymbolfolge"  $ \langle v_\nu \rangle$  mit  $ v_\nu \in \{\rm L, \ H\}$.

Die Laufvariable  $\nu$   kann Werte zwischen  $1$  und  $N$  annehmen.

Ein Vergleich mit dem Blockschaltbild im  "$\text{Beispiel 1}$"  zeigt: 

• Der  "Digitale Kanal"  ist ein vereinfachendes Modell des analogen Übertragungskanals einschließlich der technischen Sende– und Empfangseinrichtungen. 

• Vereinfachend deshalb,  weil dieses Modell sich lediglich auf die auftretenden Übertragungsfehler bezieht,  dargestellt durch die Fehlerfolge  $ \langle e_\nu \rangle$  mit

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.25cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.25cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

• Während  $\rm L$  und  $\rm H$  die möglichen Symbole bezeichnen,  die hier für  "Low"  und  "High"  stehen,  ist  $ e_\nu \in \{\rm 0, \ 1\}$  ein reeller Zahlenwert. br>Hinweis.     Oft werden die Symbole auch als  $ q_\nu \in \{\rm 0, \ 1\}$  und  $ v_\nu \in \{\rm 0, \ 1\}$  definiert.  Um Verwechslungen zu vermeiden,  haben wir hier die etwas ungewöhnliche Nomenklatur verwendet.
  

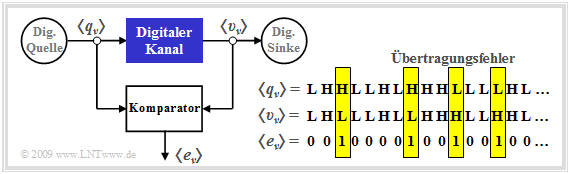
Die in der Grafik angegebene Fehlerfolge  $ \langle e_\nu \rangle$

• ergibt sich durch den Vergleich der beiden Binärfolgen   $ \langle q_\nu \rangle$   und   $ \langle v_\nu \rangle$,
  

• beinhaltet nur Informationen über die Abfolge der Übertragungsfehler und damit weniger Information als ein analoges Kanalmodell,
  

• wird zweckmäßigerweise durch einen Zufallsprozess mit nur wenigen Parametern angenähert.
  
  

$\text{Fazit:}$  Die  Fehlerfolge  $ \langle e_\nu \rangle$  erlaubt Aussagen über die Fehlerstatistik, zum Beispiel ob es sich um so genannte

1. statistisch unabhängige Fehler, oder
   
2. Bündelfehler
   
   

handelt.  Das folgende Beispiel soll diese beiden Fehlerarten verdeutlichen.

$\text{Beispiel 2:}$  In der folgenden Grafik sehen wir in der Mitte das BMP–Bild  "Weiß"  mit $300 × 200$ Pixeln.

BMP–Bild  "Weiß"  mit unabhängigen Fehlern  (links)  bzw. Bündelfehlern  (rechts)

• Das linke Bild zeigt die Verfälschung mit statistisch unabhängigen Fehlern   ⇒   BSC–Modell.

• Das rechte Bild verdeutlicht einen Bündelfehlerkanal   ⇒   Gilbert–Elliott–Modell.
  

Anmerkungen:

1. Eine  "BMP–Grafik"  stets zeilenweise abgespeichert,  was an den Fehlerbündeln im rechten Bild zu erkennen ist.
2. Die mittlere Fehlerwahrscheinlichkeit beträgt in beiden Fällen  $2.5\%$,   ⇒   im Mittel wird jedes $40.$ Pixel verfälscht  $($hier:   weiß  ⇒  schwarz$)$.

Beispielhafte Anwendung von digitalen Kanalmodellen

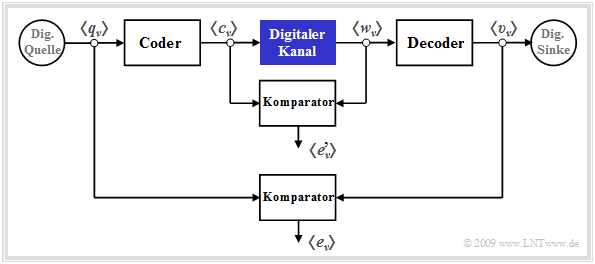
Digitale Kanalmodelle finden vorzugsweise Anwendung bei einer kaskadierten Übertragung,  wie in der folgenden Grafik dargestellt.  Man erkennt aus dieser Darstellung:

Modell eines Übertragungssystems mit Coder/Decoder

• Das innere Übertragungssystem – bestehend aus Modulator, Analogkanal, Störung, Demodulator, Empfangsfilter, Entscheider und Taktrückgewinnung – ist im blau markierten Block  "Digitaler Kanal"  zusammengefasst.
  

• Dieser innere Block wird auschließlich durch seine Fehlerfolge  $ \langle e\hspace{0.05cm}'_\nu \rangle$  charakterisiert,  die sich auf seine Eingangssymbolfolge  $ \langle c_\nu \rangle$  und Ausgangssymbolfolge  $ \langle w_\nu \rangle$  bezieht.  Es ist offensichtlich,  dass dieses Kanalmodell weniger Informationen liefert als ein detailliertes Analogmodell unter Berücksichtigung aller Komponenten.

• Dagegen bezieht sich die  "äußere” Fehlerfolge"  $ \langle e_\nu \rangle$  auf die Quellensymbolfolge  $ \langle q_\nu \rangle$  und die Sinkensymbolfolge  $ \langle v_\nu \rangle$  und damit auf das Gesamtsystem einschließlich der spezifischen Codierung und des empfängerseitigen Decoders.
  

• Der Vergleich der beiden Fehlerfolgen mit und ohne Berücksichtigung von Coder/Decoder erlaubt Rückschlüsse auf die Effizienz der zugrundeliegenden Codierung und Decodierung.  Diese beiden Komponenten sind dann und nur dann sinnvoll,  wenn der äußere Komparator im Mittel weniger Fehler anzeigt als der innere.
  

Fehlerfolge und mittlere Fehlerwahrscheinlichkeit

$\text{Definition:}$  Das Übertragungsverhalten eines Binärsystems wird durch die  Fehlerfolge  $ \langle e_\nu \rangle$  vollständig beschrieben:

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

• Hieraus kann die  (mittlere)   Bitfehlerwahrscheinlichkeit  wie folgt berechnet werden:

\[p_{\rm M} = {\rm E}\big[e \big] = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.\]

• Vorausgesetzt ist hierbei,  dass der die Fehlentscheidungen erzeugende Zufallsprozess  "stationär"  und  "ergodisch"  ist,  so dass man die Fehlerfolge  $ \langle e_\nu \rangle$  formal auch durch die Zufallsgröße  $e \in \{0, \ 1\}$  vollständig beschreiben kann.  Der Übergang von der Zeit– zur Scharmittelung ist also zulässig.

Hinweis:  

1. In allen anderen  $\rm LNTwww $–Büchern wird die mittlere Bitfehlerwahrscheinlichkeit mit  $p_{\rm B}$  bezeichnet.
2. Zur Vermeidung von Verwechslungen im Zusammenhang mit dem  "Gilbert–Elliott–Modell"  ist diese hier vorgenommene Umbenennung unvermeidbar.
3. Wir sprechen nachfolgend nicht mehr von der  "Bitfehlerwahrscheinlichkeit",  sondern nur noch von der  "mittleren Fehlerwahrscheinlichkeit"  $p_{\rm M}$.
   

Fehlerkorrelationsfunktion

$\text{Definition:}$  Eine wichtige Beschreibungsgröße der digitalen Kanalmodelle ist auch die  Fehlerkorrelationsfunktion  – abgekürzt  $\rm FKF$:

\[\varphi_{e}(k) = {\rm E}\big [e_{\nu} \cdot e_{\nu + k}\big ] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]

Die Fehlerkorrelationsfunktion weist folgende Eigenschaften auf:

• $\varphi_{e}(k) $  gibt die  (zeitdiskrete)  "Autokorrelationsfunktion"  der ebenfalls zeitdiskreten Zufallsgröße  $e$  an.  Die überstreichende Linie in der rechten Gleichung kennzeichnet die Zeitmittelung.
  

• Der Fehlerkorrelationswert  $\varphi_{e}(k) $  liefert statistische Aussagen bezüglich zwei um  $k$  auseinander liegende Folgenelemente,  zum Beispiel über  $e_{\nu}$  und  $e_{\nu+ k}$.  Die dazwischen liegenden Elemente  $e_{\nu+ 1}$, ... , $e_{\nu+ k-1}$  beeinflussen den  $\varphi_{e}(k)$–Wert nicht.
  

• Bei stationren Folgen gilt unabhängig von der der Fehlerstatistik wegen  $e \in \{0, \ 1\}$  stets:

\[\varphi_{e}(k = 0) = {\rm E}\big[e_{\nu} \cdot e_{\nu}\big] = {\rm E}\big[e^2\big]= {\rm E}\big[e\big]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},\]

\[\varphi_{e}(k \rightarrow \infty) = {\rm E}\big[e_{\nu}\big] \cdot {\rm E}\big[e_{\nu + k}\big] = p_{\rm M}^2\hspace{0.05cm}.\]

• Die Fehlerkorrelationsfunktion ist eine zumindest schwach abfallende Funktion.  Je langsamer der Abfall der FKF–Werte erfolgt, desto länger ist das Gedächtnis des Kanals und um so weiter reichen die statistischen Bindungen der Fehlerfolge.
  
  

$\text{Beispiel 3:}$  Bei einer Binärübertragung werden  $100$  der insgesamt  $N = 10^5$  übertragenen Binärsymbole verfälscht   ⇒   die Fehlerfolge  $ \langle e_\nu \rangle$  beteht aus 

• $100$  Einsen
• und  $99900$  Nullen.

Daraus folgt:

1. Die mittlere Fehlerwahrscheinlichkeit beträgt  $p_{\rm M} =10^{-3}$.
2. Die Fehlerkorrelationsfunktion  $\varphi_{e}(k)$  beginnt bei  $p_{\rm M} =10^{-3}$  $($für  $k = 0)$  und tendiert für sehr große  $k$–Werte gegen  $p_{\rm M}^2 =10^{-6}$ $($für  $k = \to \infty)$.
3. Über den tatsächlichen Verlauf von  $\varphi_{e}(k)$  ist mit den hier gemachten Angaben bisher noch keine Aussage möglich.

Zusammenhang zwischen Fehlerfolge und Fehlerabstand

$\text{Definition:}$  Der  Fehlerabstand  $a$  bezeichnet die Anzahl der zwischen zwei Kanalfehlern richtig übertragenen Symbole plus  $1$. 

Zur Definition des Fehlerabstands

Die Grafik verdeutlicht diese Definition:

• Jede in der Fehlerfolge  $ \langle e_\nu \rangle$  enthaltene Information über das Übertragungsverhalten des digitalen Kanals ist auch in der Folge  $ \langle a_n \rangle$  der Fehlerabstände enthalten.

• Da die Folgen  $ \langle e_\nu \rangle$  und  $ \langle a_n \rangle$  nicht synchron laufen,  verwenden wir unterschiedliche Indizes  $(\nu$  bzw.  $n)$.

Aus der Grafik erkennt man insbesondere:

• Da das erste Symbol richtig übertragen wurde  $(e_1 = 0)$  und das zweite falsch  $(e_2 = 1)$,  ist der Fehlerabstand  $a_1 = 2$.
  

• $a_2 = 4$  sagt aus,  dass zwischen den beiden ersten Fehlern  $(e_2 = 1, \ e_5 = 1)$  drei Symbole richtig übertragen wurden.
  

• Folgen zwei Fehler direkt aufeinander,  so ist der Fehlerabstand wie in obiger Grafik gleich  $a_3=1$.
  

• Das Ereignis  "$a = k$"  bedeutet gleichzeitig   $k-1$   fehlerfreie Symbole zwischen zwei Fehlern.

• Ist zum Zeitpunkt  $\nu$  ein Fehler aufgetreten,  so folgt mit  "$a = k$"  der nächste Fehler genau zum Zeitpunkt  $\nu + k$.
  

• Der Wertevorrat der Zufallsgröße  $a$  ist die Menge der natürlichen Zahlen im Gegensatz zur binären Zufallsgröße  $e$:

$$a \in \{ 1, 2, 3, ... \}\hspace{0.05cm},\hspace{0.5cm} e \in \{ 0, 1 \}\hspace{0.05cm}.$$

• Die mittlere Fehlerwahrscheinlichkeit lässt sich aus beiden Zufallsgrößen ermitteln:

$${\rm E}\big[e \big] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm},$$

$$ {\rm E}\big[a \big] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.$$

$\text{Beispiel 4:}$ 

• In der skizzierten Folge sind  $16$  der insgesamt  $N = 40$  Symbole verfälscht   ⇒   $p_{\rm M} = 0.4$.

• Der Erwartungswert der Fehlerabstände ergibt entsprechend

\[{\rm E}\big[a \big] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = {1}/{p_{\rm M} }\hspace{0.05cm}.\]

Fehlerabstandsverteilung

Die  "Wahrscheinlichkeitsdichtefunktion"  $\rm (WDF)$  der diskreten Zufallsgröße  $a \in \{1, 2, 3, \text{...}\}$  setzt sich entsprechend dem Kapitel  "WDF-Definition für diskrete Zufallsgrößen"  im Buch  "Stochastische Signaltheorie"  aus einer  (unendlichen)  Summe von Diracfunktionen zusammen:

\[f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.\]

• Wir bezeichnen diese spezielle WDF als  "Fehlerabstandsdichtefunktion".  Die Wahrscheinlichkeit,  dass der Fehlerabstand  $a$  exakt gleich  $k$  ist,  lässt sich anhand der Fehlerfolge durch die folgende bedingte Wahrscheinlichkeit ausdrücken:

\[{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} \text{...} \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.\]

• Im Buch  "Stochastische Signaltheorie"  finden Sie ebenfalls die Definition der  "Verteilungsfunktion"  der diskreten Zufallsgröße  $a$:

\[F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.\]

• Diese Funktion ergibt sich aus der WDF  $f_a(a)$  durch Integration von  $1$  bis  $k$.  Die Funktion  $F_a(k)$  kann Werte zwischen  $0$  und  $1$   (einschließlich dieser beiden Grenzen)  annehmen und ist schwach monoton ansteigend.
  

Im Zusammenhang mit den digitalen Kanalmodellen wird in der Literatur von dieser üblichen Definition abgewichen.

$\text{Definition:}$  Vielmehr gibt hier die  Fehlerabstandsverteilung  $\rm (FAV)$  die Wahrscheinlichkeit an,  dass der Fehlerabstand  $a$  größer oder gleich  $k$  ist:

\[V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.\]

• Insbesondere gilt:  

$$V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm} \lim_{k \rightarrow \infty}V_a(k ) = 0 \hspace{0.05cm}.$$

Zwischen der monoton ansteigenden Funktion  $F_a(k)$  und der monoton abfallenden Funktion  $V_a(k)$  gilt folgender Zusammenhang:

\[F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.\]

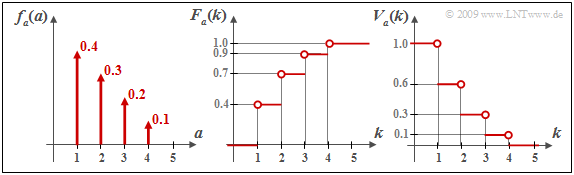
$\text{Beispiel 5:}$  Die Grafik zeigt links eine willkürliche diskrete Fehlerabstandsdichtefunktion  $f_a(a)$  und die daraus resultierenden  integrierten Funktionen

Diskrete Wahrscheinlichkeitsdichte  $f_a(a)$  und die Funktionen  $F_a(k )$  and  $V_a(k )$

• $F_a(k ) = {\rm Pr}(a \le k)$   ⇒   mittlere Skizze, sowie
• $V_a(k ) = {\rm Pr}(a \ge k)$   ⇒   rechte Skizze.
  

Beispielsweise ergibt sich für  $k = 2$:

\[F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, \]

\[\Rightarrow \hspace{0.3cm} F_a( k =2 ) = 1-V_a(k = 3)= 0.7\hspace{0.05cm}, \]

\[ V_a(k =2 ) = 1 - {\rm Pr}(a = 1) \hspace{0.05cm},\]

\[\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.\]

Für  $k = 4$  erhält man folgende Resultate:

\[F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 \hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) \hspace{0.05cm}.\]

Aufgaben zum Kapitel

Aufgabe 5.1:  Fehlerabstandsverteilung

Aufgabe 5.2:  Fehlerkorrelationsfunktion