Kanalcodierung/Soft–in Soft–out Decoder: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{Header |Untermenü=Iterative Decodierverfahren |Vorherige Seite=Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken |Nächste Seite=Grundlegendes z…“) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 61: | Zeile 61: | ||
*läge bei Block 3 und 4 nahe bei 0.<br> | *läge bei Block 3 und 4 nahe bei 0.<br> | ||
| + | == Zuverlässigkeitsinformation – Log Likelihood Ratio (1) == | ||
| + | <br> | ||
| + | Es sei <i>x</i> ∈ {+1, –1} eine binäre Zufallsvariable mit den Wahrscheinlichkeiten Pr(<i>x</i> = +1) und Pr(<i>x</i> = –1). Für die Codierungstheorie erweist es sich als zweckmäßig hinsichtlich der Rechenzeiten, wenn man anstelle der Wahrscheinlichkeiten Pr(<i>x</i> = ±1) den natürlichen Logarithmus des Quotienten heranzieht.<br> | ||
| + | {{Definition}}''':''' Das <b>Log–Likelihood–Verhältnis</b> (kurz: der <i>L</i>–Wert, englisch: <i>Log–Likelihood Ratio</i>, LLR) der Zufallsgröße <i>x</i> ∈ {+1, –1} lautet: | ||
| + | :<math>L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.</math> | ||
| + | Bei unipolarer/symbolhafter Darstellung (+1 → 0 und –1 → 1) gilt entsprechend mit <i>ξ</i> ∈ {0, 1}: | ||
| + | :<math>L(\xi)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(\xi = 0)}{{\rm Pr}(\xi = 1)}\hspace{0.05cm}.</math>{{end}}<br> | ||
| + | Nachfolgend ist der nichtlineare Zusammenhang zwischen Pr(<i>x</i> = ±1) und <i>L</i>(<i>x</i>) angegeben. Ersetzt man Pr(<i>x</i> = +1) durch Pr(<i>ξ</i> = 0), so gibt die mittlere Zeile den <i>L</i>–Wert der unipolaren Zufallsgröße <i>ξ</i> an.<br> | ||
| + | [[Datei:P ID2975 KC T 4 1 S2a v1.png|Wahrscheinlichkeit und <i>L</i>–Wert|class=fit]]<br> | ||
| + | Man erkennt: | ||
| + | *Der wahrscheinlichere Zufallswert von <i>x</i> ∈ {+1, –1} ist durch sign <i>L</i>(<i>x</i>) ⇒ <b>Vorzeichen</b> gegeben.<br> | ||
| + | *Dagegen gibt der <b>Betrag</b> |<i>L</i>(<i>x</i>)| die Zuverlässigkeit für das Ergebnis sign(<i>L</i>(<i>x</i>)) an.<br><br> | ||
| + | {{Beispiel}}''':''' | ||
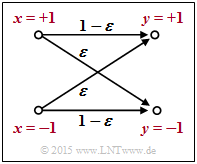
| + | [[Datei:P ID2976 KC T 4 1 S2b v2.png|rahmenlos|rechts|BSC–Modell]] Wir betrachten das skizzierte BSC–Modell mit bipolarer Darstellung. Hier gilt mit der Verfälschungswahrscheinlichkeit <i>ε</i> = 0.1 sowie den beiden Zufallsgrößen <i>x</i> ∈ {+1, –1} und <i>y</i> ∈ {+1, –1} am Eingang und Ausgang des Kanals: | ||
| + | :<math>L(y\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.15cm} = \hspace{-0.15cm} | ||
| + | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} = </math> | ||
| + | :<math>\hspace{-0.15cm} = \hspace{-0.15cm} | ||
| + | \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ | ||
| + | {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, | ||
| + | \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}</math> | ||
| + | Beispielsweise ergeben sich für <i>ε</i> = 0.1 folgende Zahlenwerte (vergleiche obere Tabelle): | ||
| + | :<math>L(y = +1\hspace{0.05cm}|\hspace{0.05cm}x) = | ||
| + | {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.2cm} | ||
| + | L(y = -1\hspace{0.05cm}|\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.</math> | ||
| + | |||
| + | Dieses Beispiel zeigt, dass man die sog. <i>L</i>–Wert–Algebra auch auf bedingte Wahrscheinlichkeiten anwenden kann. In Aufgabe Z4.1 wird das BEC–Modell in ähnlicher Weise beschrieben.{{end}}<br> | ||
| + | |||
| + | == Zuverlässigkeitsinformation – Log Likelihood Ratio (2) == | ||
| + | <br> | ||
| + | Wir betrachten nun den AWGN–Kanal mit den beiden bedingten Wahrscheinlichkeitsdichtefunktionen | ||
| + | |||
| + | :<math>f_{y \hspace{0.03cm}| \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} | ||
| + | \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},</math> | ||
| + | :<math>f_{y \hspace{0.03cm}| \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} | ||
| + | \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | ||
| + | |||
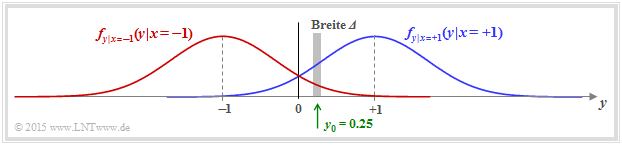
| + | In der Grafik sind zwei beispielhafte Gaußfunktionen als blaue bzw. rote Kurve dargestellt.<br> | ||
| + | |||
| + | [[Datei:P ID2977 KC T 4 1 S2c v3.png|Bedingte AWGN–Dichtefunktionen|class=fit]]<br> | ||
| + | |||
| + | Die gesamte WDF des Ausgangssignals <i>y</i> ergibt sich aus der (gleich) gewichteten Summe: | ||
| + | |||
| + | :<math>f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}| \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} | ||
| + | f_{y \hspace{0.03cm}| \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=-1 ) | ||
| + | \big ] | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | Berechnen wir nun die Wahrscheinlichkeit, dass der Empfangswert <i>y</i> in einem (sehr) schmalen Intervall der Breite <i>Δ</i> um <i>y</i><sub>0</sub> = 0.25 liegt, so erhält man näherungsweise | ||
| + | |||
| + | :<math>{\rm Pr} (|y - y_0| \le{\it \Delta}/2 \hspace{0.05cm} | ||
| + | \Big | \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} | ||
| + | \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},</math> | ||
| + | :<math>{\rm Pr} (|y - y_0| \le {\it \Delta}/2 \hspace{0.05cm} | ||
| + | \Big | \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} | ||
| + | \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | ||
| + | |||
| + | Die etwas größeren senkrechten Striche bezeichnen die Bedingungen, die kleineren die Betragsbildung.<br> | ||
| + | |||
| + | Der <i>L</i>–Wert der bedingten Wahrscheinlichkeit in Vorwärtsrichtung (das bedeutet: Ausgang <i>y</i> für einen gegebenen Eingang <i>x</i>) ergibt sich somit als der Logarithmus des Quotienten beider Ausdrücke: | ||
| + | |||
| + | :<math>L(y = y_0\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.1cm} = \hspace{-0.1cm} | ||
| + | {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = | ||
| + | {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ]\hspace{0.15cm} = </math> | ||
| + | :<math>\hspace{2.4cm} = \hspace{-0.1cm} \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. </math> | ||
| + | |||
| + | Ersetzen wir nun die Hilfsgröße <i>y</i><sub>0</sub> durch die (allgemeine) Zufallsgröße <i>y</i> am AWGN–Ausgang, so lautet das Endergebnis: | ||
| + | |||
| + | :<math>L(y \hspace{0.05cm}|\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. </math> | ||
| + | |||
| + | Hierbei ist <i>K</i><sub>L</sub> = 2/<i>σ</i><sup>2</sup> eine Konstante, die allein von der Streuung der Gaußschen Störung abhängt.<br> | ||
Version vom 17. Januar 2017, 15:52 Uhr
Inhaltsverzeichnis
Hard Decision vs. Soft Decision (1)
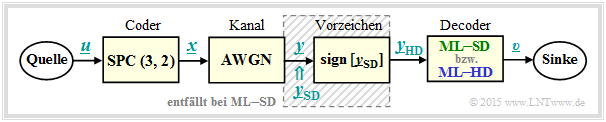
Zur Hinleitung auf die Thematik dieses vierten und letzten Kapitels und zur Motivation betrachten wir das folgende Nachrichtenübertragungssystem mit Codierung.
Nachfolgend werden alle Symbole in bipolarer Darstellung angegeben: „0” → „+1” und „1” → „–1”.
- Die Symbolfolge u = (u1, u2) wird der Coderfolge x = (x1, x2, x3) = (u1, u2, p) zugeordnet, wobei für das Paritybit p = u1 ⊕ u2 gilt ⇒ Single Parity–check Code ⇒ SPC (3, 2, 2).
- Der AWGN–Kanal verändert die Binärsymbole xi ∈ {+1, –1} zu reellwertigen Ausgangswerten yi, z.B. im Block 4 der unteren Tabelle: x1 = +1 ⇒ y1 = +0.9 und x3 = –1 ⇒ y3 = +0.1.
- Die Decodierung geschieht gemäß dem Kriterium Maximum Likelihood (block–wise ML), wobei zwischen Hard Decision (ML–HD) und Soft Decision (ML–SD) zu unterscheiden ist.
- Das obige Blockschaltbild in seiner Gesamtheit entspricht ML–HD. Hier werden zur Detektion nur die Vorzeichen der AWGN–Ausgangswerte entsprechend yHD, i = sign[ySD, i] ausgewertet.
- Bei Soft Decision (ML–SD) verzichtet man auf den schraffierten Block in obigem Blockschaltbild und wertet direkt die wertkontinuierlichen Eingangsgrößen ySD, i aus.
Aus der Beispieltabelle erkennt man:
- Hard Decision ⇒ die Symbolfolge υHD ergibt sich aus den hart entschiedenen Kanalwerten yHD (blaue Hinterlegung): Es werden nur die beiden ersten Blöcke fehlerfrei decodiert.
- Soft Decision ⇒ die Symbolfolge υSD ergibt sich aus den „weichen” Kanalausgangswerten ySD (grüne Hinterlegung): Nun wird in diesem Beispiel auch der dritte Block richtig entschieden.
Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.
Hard Decision vs. Soft Decision (2)
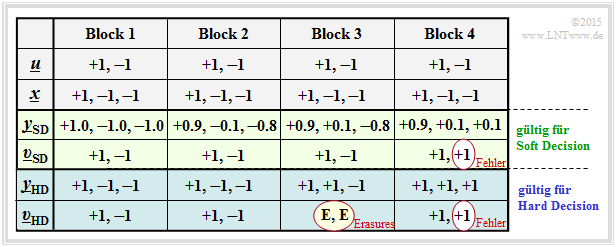
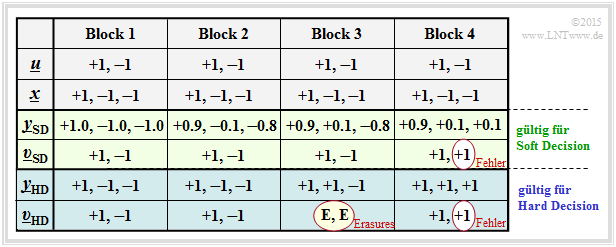
Für alle Spalten der folgenden Tabelle wird vorausgesetzt:
- der Nachrichtenblock u = (0, 1), bipolar darstellbar als (+1, –1),
- der SPC (3, 2)–codierte Block x = (0, 1, 1) bzw. in Bipolardarstellung (+1, –1, –1).
Die vier Blöcke unterscheiden sich also nur durch unterschiedliche AWGN–Realisierungen.
Die Tabelle ist wie folgt zu interpretieren:
- Bei idealem Kanal entsprechend Block 1 ⇒ x = ySD = yHD gibt es keinen Unterschied zwischen der (blauen) herkömmlichen ML–HD –Variante und der (grünen) ML–SD –Variante.
- Der Block 2 demonstriert geringe Signalverfälschungen. Wegen yHD = x (das heißt, dass der Kanal die Vorzeichen nicht verfälscht) liefert auch ML–HD das richtige Ergebnis υHD = u.
- Dagegen gilt im dritten Block yHD ≠ x und es gibt auch keine SPC (3, 2)–Zuordnung u ⇒ yHD. Der ML–Decoder kann hier nur durch die Ausgabe υHD = (E, E) vermelden, dass er bei der Decodierung dieses Blocks gescheitert ist. „E” steht hierbei für Erasure (deutsch: Auslöschung).
- Auch der Soft Decision Decoder erkennt, dass eine Decodierung anhand der Vorzeichen nicht funktioniert. Anhand der ySD–Werte erkennt er aber, dass mit großer Wahrscheinlichkeit das zweite Bit verfälscht wurde und entscheidet sich für die richtige Symbolfolge υSD = (+1, –1) = u.
- Im vierten Block werden durch den AWGN–Kanal sowohl die Vorzeichen von Bit 2 als auch von Bit 3 verändert, was zum Ergebnis υHD = (+1, +1) ≠ u (+1, –1) führt ⇒ ein Blockfehler und gleichzeitig ein Bitfehler. Auch der Soft Decision Decoder liefert hier das gleiche falsche Ergebnis.
Die Decodiervariante ML–SD bietet gegenüber ML–HD zudem den Vorteil, dass man relativ einfach jedes Decodierergebnis mit einem Zuverlässigkeitswert versehen kann (in obiger Tabelle ist dieser allerdings nicht angegeben). Dieser Zuverlässigkeitswert
- hätte bei Block 1 seinen Maximalwert,
- wäre bei Block 2 deutlich kleiner,
- läge bei Block 3 und 4 nahe bei 0.
Zuverlässigkeitsinformation – Log Likelihood Ratio (1)
Es sei x ∈ {+1, –1} eine binäre Zufallsvariable mit den Wahrscheinlichkeiten Pr(x = +1) und Pr(x = –1). Für die Codierungstheorie erweist es sich als zweckmäßig hinsichtlich der Rechenzeiten, wenn man anstelle der Wahrscheinlichkeiten Pr(x = ±1) den natürlichen Logarithmus des Quotienten heranzieht.
\[L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.\]
Bei unipolarer/symbolhafter Darstellung (+1 → 0 und –1 → 1) gilt entsprechend mit ξ ∈ {0, 1}:
\[L(\xi)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(\xi = 0)}{{\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]
Nachfolgend ist der nichtlineare Zusammenhang zwischen Pr(x = ±1) und L(x) angegeben. Ersetzt man Pr(x = +1) durch Pr(ξ = 0), so gibt die mittlere Zeile den L–Wert der unipolaren Zufallsgröße ξ an.
Man erkennt:
- Der wahrscheinlichere Zufallswert von x ∈ {+1, –1} ist durch sign L(x) ⇒ Vorzeichen gegeben.
- Dagegen gibt der Betrag |L(x)| die Zuverlässigkeit für das Ergebnis sign(L(x)) an.
\[L(y\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.15cm} = \hspace{-0.15cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} = \] \[\hspace{-0.15cm} = \hspace{-0.15cm} \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}\]
Beispielsweise ergeben sich für ε = 0.1 folgende Zahlenwerte (vergleiche obere Tabelle):
\[L(y = +1\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.2cm} L(y = -1\hspace{0.05cm}|\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]
Dieses Beispiel zeigt, dass man die sog. L–Wert–Algebra auch auf bedingte Wahrscheinlichkeiten anwenden kann. In Aufgabe Z4.1 wird das BEC–Modell in ähnlicher Weise beschrieben.
Zuverlässigkeitsinformation – Log Likelihood Ratio (2)
Wir betrachten nun den AWGN–Kanal mit den beiden bedingten Wahrscheinlichkeitsdichtefunktionen
\[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\] \[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
In der Grafik sind zwei beispielhafte Gaußfunktionen als blaue bzw. rote Kurve dargestellt.
Die gesamte WDF des Ausgangssignals y ergibt sich aus der (gleich) gewichteten Summe:
\[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}| \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}| \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]
Berechnen wir nun die Wahrscheinlichkeit, dass der Empfangswert y in einem (sehr) schmalen Intervall der Breite Δ um y0 = 0.25 liegt, so erhält man näherungsweise
\[{\rm Pr} (|y - y_0| \le{\it \Delta}/2 \hspace{0.05cm} \Big | \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\] \[{\rm Pr} (|y - y_0| \le {\it \Delta}/2 \hspace{0.05cm} \Big | \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
Die etwas größeren senkrechten Striche bezeichnen die Bedingungen, die kleineren die Betragsbildung.
Der L–Wert der bedingten Wahrscheinlichkeit in Vorwärtsrichtung (das bedeutet: Ausgang y für einen gegebenen Eingang x) ergibt sich somit als der Logarithmus des Quotienten beider Ausdrücke:
\[L(y = y_0\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ]\hspace{0.15cm} = \] \[\hspace{2.4cm} = \hspace{-0.1cm} \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]
Ersetzen wir nun die Hilfsgröße y0 durch die (allgemeine) Zufallsgröße y am AWGN–Ausgang, so lautet das Endergebnis:
\[L(y \hspace{0.05cm}|\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]
Hierbei ist KL = 2/σ2 eine Konstante, die allein von der Streuung der Gaußschen Störung abhängt.