Aufgaben:Aufgabe 4.7: Mehrere parallele Gaußkanäle

• Zurück zum Buch

Einige häufig verwendete Signalraumkonstellationen

Die Kanalkapazität des AWGN–Kanals  ⇒ $Y = X + N$ wurde im Theorieteil wie folgt angegeben (mit Zusatz–Einheit „bit”):

$$C_{\rm AWGN}(P_X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$

Die verwendeten Größen haben folgende Bedeutung:

• $P_X$ ist die Sendeleistung  ⇒  Varianz der Zufallsgröße $X$,
• $P_N$ ist die Störleistung  ⇒  Varianz der Zufallsgröße $N$.

Werden $K$ identische Gaußkanäle parallel genutzt, so gilt für die Gesamtkapazität:

$$C_K(P_X) = K \cdot C_{\rm AWGN}(P_X/K) \hspace{0.05cm}.$$

Hierbei ist berücksichtigt, dass

• in jedem Kanal die gleiche Störleistung $P_N$ vorliegt,
• somit jeder Kanal die gleiche Sendeleistung erhält,
• die Gesamtleistung genau wie im Fall $K = 1$ gleich $P_X$ ist.

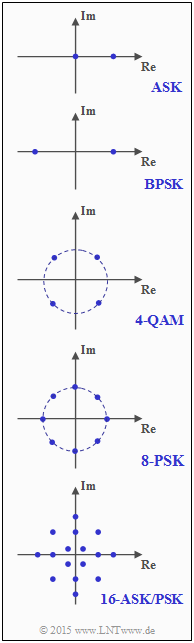
In nebenstehender Grafik sind die Signalraumpunkte für einige digitale Modulationsverfahren angegeben:

• Amplitude Shift Keying (ASK),
• Binary Phase Shift Keying (BPSK),
• Quadratur-Amplitudenmodulation (hier: 4-QAM),
• Phase Shift Keying (hier: 8–PSK für GSM Evolution),
• Kombinierte ASK/PSK-Modulation (hier: 16-ASK/PSK).

Zu Beginn dieser Aufgabe ist zu prüfen, welcher $K$–Parameter für die einzelnen Verfahren gültig ist.

Hinweise:

• Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
• Bezug genommen wird insbesondere auf die Seite Parallele Gaußkanäle.
• Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log”  ⇒  „log₂” verwendet.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

{Welche Parameter K gelten für die folgenden Modulationsverfahren?

$K \ = \ $ $\text{(bei ASK)}$

$K \ = \ $ $\text{(bei BPSK)}$

$K \ = \ $ $\text{(bei 4-QAM)}$

$K \ = \ $ $\text{(bei 8-PSK)}$

$K \ = \ $ $\text{(16-ASK/PSK)}$

2

Welche Kanalkapazität $C_K$ ergibt sich für $K$ gleich gute Kanäle (jeweils mit der Störleistung $P_N$ und der Sendeleistung $P_X(K)$?

	Es gilt   $C_K = K/2 \cdot \log_2 [1 + P_X/P_N]$.
	Es gilt   $C_K = K/2 \cdot \log_2 [1 + P_X/(K \cdot P_N)]$.
	Es gilt   $C_K = 1/2 \cdot \log_2 [1 + P_X/P_N]$.

3

Welche Kapazitäten ergeben sich für $P_X/P_N = 15$?

$K = 1\text{:} \ \ C_K \ = \ $

$K = 2\text{:} \ \ C_K \ = \ $

$K = 4\text{:} \ \ C_K \ = \ $

4

Gibt es bezüglich der Kanalzahl $K$ ein (theoretisches) Optimum?

	Ja:   Die größte Kanalkapazität ergibt sich für $K = 2$.
	Ja:   Die größte Kanalkapazität ergibt sich für $K = 4$.
	Nein:   Je größer $K$, desto größer ist die Kanalkapazität.
	Der Grenzwert für $K \to \infty$ (in bit) ist $C_K = P_X/P_N/2/\ln (2)$ in „bit&rdqu;o.

Musterlösung

Musterlösung

a)  Der Parameter K ist gleich der Dimension der Signalraumdarstellung:

• Für ASK und BPSK ist K = 1.
• Für die Konstellationen 3 – 5 gilt K = 2 (orthogonale Modulation mit Cosinus und Sinus).

b)  Für jeden der Kanäle (1 ≤ k ≤ K) beträgt die Kanalkapazität C_k = 1/2 · log₂ (1 + (P_X/k)/P_N). Die Gesamtkapazität ist dann um den Faktor K größer  ⇒  Lösungsvorschlag 2: $$C_K(P_X) = \sum_{k= 1}^K \hspace{0.1cm}C_k = \frac{K}{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{K \cdot P_N} \right )\hspace{0.05cm}.$$ Der Lösungsvorschlag 1 ist zu positiv. Dieser würde bei Begrenzung der Gesamtleistung auf K · P_X gelten. Der Vorschlag 3 würde dagegen bedeuten, dass man durch die Nutzung mehrerer unabhängiger Kanäle keine Kapazitätssteigerung erreicht, was offensichtlich nicht zutrifft.

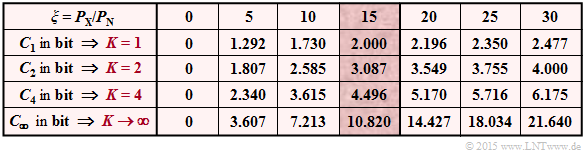
c)  Die folgende Tabelle zeigt die Ergebnisse für K = 1, K = 2 und K = 4 und verschiedene Signal–zu–Störleistungsverhältnisse P_X/P_N.

Für P_X/P_N = 15 (markierte Spalte) ergibt sich:

• K = 1:   C_K = 1/2 · log₂ (16) = 2.000 bit,
• K = 2:   C_K = 1 · log₂ (8.5) = 3.087 bit,
• K = 4:   C_K = 2 · log₂ (4.75) = 4.496 bit.

d)  Schon aus obiger Tabelle ist ersichtlich, dass der erste Lösungsvorschlag falsch sein muss. Richtig sind vielmehr die Lösungsvorschläge 3 und 4, wie die nachfolgende Rechnung zeigt:

• Wir schreiben die Kanalkapazität mit „ln” und der Abkürzung ξ = P_X/P_N:

$$C_{\rm nat}(\xi, K) = \frac{K}{2} \cdot {\rm ln}\hspace{0.05cm}\left ( 1 + \frac{\xi}{K} \right )\hspace{0.05cm}.$$

• Für große K–Werte, also für kleine Werte von ε = ξ/K gilt dann:

$${\rm ln}\hspace{0.05cm}\left ( 1 + \varepsilon \right )= \varepsilon - \frac{\varepsilon^2}{2} + \frac{\varepsilon^3}{3} - ... \hspace{0.3cm}\Rightarrow \hspace{0.3cm} C_{\rm nat}(\xi, K) = \frac{K}{2} \cdot \left [ \frac{\xi}{K} - \frac{\xi^2}{2K^2} + \frac{\xi^3}{3K^3} - ... \right ]$$ $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm} C_{\rm bit}(\xi, K) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \cdot \left [ 1 - \frac{\xi}{2K} + \frac{\xi^2}{3K^2} -\frac{\xi^3}{4K^3} + \frac{\xi^4}{5K^4} - ... \right ] \hspace{0.05cm}.$$

• Für K → ∞ ergibt sich der vorgeschlagene Wert:

$$C_{\rm bit}(\xi, K \rightarrow\infty) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} = \frac{P_X/P_N}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \hspace{0.05cm}.$$

• Für kleinere Werte von K ergibt sich stets ein kleinerer C–Wert, da

$$\frac{\xi}{2K} > \frac{\xi^2}{3K^2}\hspace{0.05cm}, \hspace{0.5cm} \frac{\xi^3}{4K^3} > \frac{\xi^4}{5K^4} \hspace{0.05cm}, \hspace{0.5cm} {\rm usw.}$$ Die letzte Zeile der Tabelle zur Teilaufgabe (c) zeigt, dass man für große ξ–Werte mit K = 4 noch weit vom theoretischen Maximum (für K → ∞) entfernt ist.