Aufgaben:Aufgabe 4.Zehn: QPSK–Kanalkapazität

• Zurück zum Buch

Kapazitätskurven für BPSK und QPSK

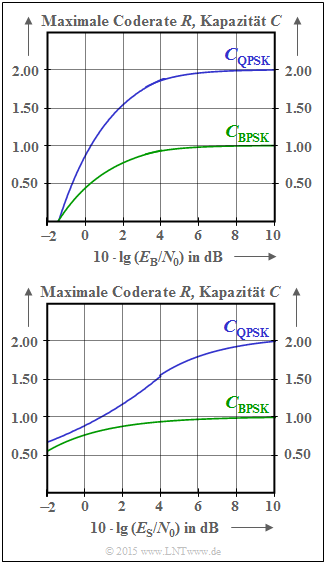
Gegeben sind die AWGN–Kanalkapazitätsgrenzkurven für die beiden Modulationsverfahren

• Binary Phase Shift Keying (BPSK),
• Quaternary Phase Shift Keying (4–PSK oder auch QPSK).

Die Kanalkapazitäten C_BPSK und C_QPSK geben gleichzeitig die maximale Coderate R an, mit der bei BPSK (bzw. QPSK) mit geeigneter Kanalcodierung die Bitfehlerwahrscheinlichkeit „p_B ≡ 0” asymptotisch erreichbar ist.

Das obere Diagramm zeigt die Abhängigkeit von der Kenngröße 10 · lg (E_B/N₀) in dB, wobei E_B die „Energie pro Informationsbit” angibt:

• Für große E_B/N₀–Werte liefert die BPSK–Kurve die maximale Coderate R ≈ 1. *Aus der QPSK–Kurve kann dagegen R ≈ 2 abgelesen werden

Die Kapazitätskurven für digitalen Eingang (jeweils mit der Einheit „bit/Symbol”),

• grüne Kurve C_BPSK(E_B/N₀) und
• blaue Kurve C_QPSK(E_B/N₀)

sollen in der Teilaufgabe (3) in Bezug gesetzt werden zu zwei Shannon–Grenzkurven, die jeweils für eine Gaußsche Eingangsverteilung gültig sind:

$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\hspace{0.05cm}R\hspace{0.05cm} E_{\rm B}}{N_0}) ,$$

$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R\hspace{0.05cm} E_{\rm B}}{N_0}) .$$

Die beiden Kurven geben gleichzeitig die maximale Coderate R an, mit der durch lange Kanalcodes eine fehlerfreie Übertragung entsprechend dem Kanalcodierungstheorem möglich ist. Natürlich gelten für C₁(E_B/N₀) bzw. C₂(E_B/N₀) unterschiedliche Randbedingungen. Welche, sollen Sie herausfinden.

Die Abszisse im unteren Diagramm ist dagegen 10 · lg (E_S/N₀) mit der „Energie pro Symbol” (E_S). Zu erkennen ist, dass die beiden Endwerte gegenüber der oberen Darstellung nicht verändert werden:

$$C_{\rm BPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm BPSK}( E_{\rm B}/{N_0} \to \infty) = 1 \ \rm bit/Symbol,$$

$$C_{\rm QPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm QPSK}( E_{\rm B}/{N_0} \to \infty) = 2 \ \rm bit/Symbol.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
• Bezug genommen wird insbesondere auf die Seite Maximale Coderate für QAM-Strukturen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Unterscheiden sich QPSK und 4–QAM aus informationstheoretischer Sicht?

	Ja.
	Nein.

2

Wie lässt sich C_QPSK(E_B/N₀) aus C_BPSK(E_B/N₀) konstruieren?

	Durch Verdopplung:   CQPSK(EB/N0) = 2 · CBPSK(EB/N0).
	Zusätzlich durch eine Verschiebung nach rechts.
	Zusätzlich durch eine Verschiebung nach links.
	CQPSK(EB/N0) kann man aus CBPSK(EB/N0) nicht konstruieren.

3

Welcher Zusammenhang besteht zu den Shannon–Grenzkurven?

	Es gilt CBPSK(EB/N0) ≤ C1(EB/N0).
	Es gilt CBPSK(EB/N0) ≤ C2(EB/N0).
	Es gilt CQPSK(EB/N0) ≤ C1(EB/N0).
	Es gilt CQPSK(EB/N0) ≤ C2(EB/N0).

4

Wie lässt sich C_QPSK(E_S/N₀) aus C_BPSK(E_S/N₀) konstruieren?

	Durch Verdopplung: CQPSK (ES/N0) = 2 · CBPSK(ES/N0).
	Zusätzlich durch eine Verschiebung nach rechts.
	Zusätzlich durch eine Verschiebung nach links.
	CQPSK(ES/N0) kann man aus CBPSK(ES/N0) nicht konstruieren.

Musterlösung

Musterlösung

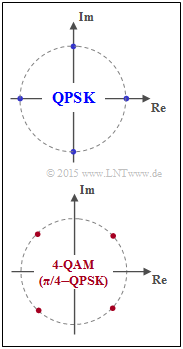
(1)  Die Grafik zeigt die Signalraumkonstellationen für

• QPSK (Quaternary Phase Shift Keying), und
• 4–QAM (vierstufige Quadraturamplitudenmodulation).

Letztere wird auch als π/4–QPSK bezeichnet. Beide sind aus informationstechnischer Sicht identisch ⇒ Antwort NEIN.

(2)  Richtig ist der Lösungsvorschlag 1: Die 4–QAM kann man als zwei BPSK–Konstellationen in orthogonalen Ebenen betrachten, wobei die Energie pro Informationsbit (E_B) in beiden Fällen gleich ist. Da entsprechend Teilaufgabe (a) die 4–QAM mit der QSPK identisch ist, gilt tatsächlich C_QPSK(E_B/N₀) = 2 · C_BPSK(E_B/N₀).



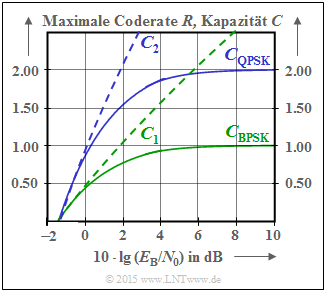
(3)  In der nebenstehenden Grafik sind die beiden angegebenen Shannon–Grenzkurven zusammen mit C_BPSK(E_B/N₀) und C_QPSK(E_B/N₀) skizziert:

$$C_1( E_{\rm B}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\hspace{0.05cm}R\hspace{0.05cm} E_{\rm B}}{N_0}) ,$$ $$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R\hspace{0.05cm} E_{\rm B}}{N_0}) .$$ Die grün–gestrichelte Kurve C₁(E_B/N₀) gilt für den AWGN–Kanal mit gaußverteiltem Eingang. Für die Coderate R = 1 sind nach dieser Kurve 10 · lg(E_B/N₀) = 1.76 dB erforderlich. Für R = 2 benötigt man 10 · lg(E_B/N₀) = 5.74 dB.

Die blau–gestrichelte Kurve C₂(E_B/N₀) gibt die Shannon–Grenze für K = 2 parallele Gaußkanäle an.
Hier benötigt man 10 · lg(E_B/N₀) = 0 dB für R = 1 bzw. 10 · lg(E_B/N₀) = 1.76 dB für R = 2.

Man erkennt aus der obigen Skizze:

• Die eindimensionale BPSK liegt im gesamten Bereich unterhalb von C₁ und damit natürlich auch unterhalb von C₂ > C₁.
• Die zweidimensionale QPSK liegt erwartungsgemäß unter der für sie relevanten Grenzkurve C₂. Sie liegt aber im unteren Bereich (bis nahezu 6 dB) oberhalb von C₁.

Richtig sind also die Lösungsvorschläge 1, 2 und 4.

(4)  Die C_QPSK(E_S/N₀)–Kurve kann ebenfalls aus C_BPSK(E_S/N₀) konstruiert werden und zwar

• durch Verdopplung

$$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$

• sowie durch eine Verschiebung um 3 dB nach rechts:

$$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$ Richtig sind die beiden ersten Lösungsvorschläge, wobei der zweite Vorschlag berücksichtigt, dass bei QPSK die Energie in einer Dimension nur E_S/2 beträgt.