Aufgaben:Aufgabe 2.4: 2D-Übertragungsfunktion

• Zurück zum Buch

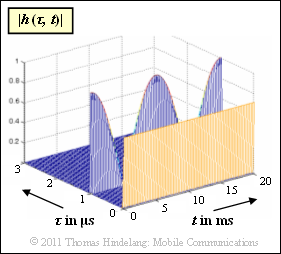
Dargestellt ist die zweidimensionale Impulsantwort $h(\tau, t)$ eines Mobilfunksystems in Betragsdarstellung. Es ist zu erkennen, dass die 2D–Impulsantwort nur für die Verzögerungszeiten $\tau = 0$ und $\tau = 1 \ \rm \mu s$ Anteile besitzt. Zu diesen Zeitpunkten gilt:

$$h(\tau = 0\,{\rm \mu s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$

$$h(\tau = 1\,{\rm \mu s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$

Für alle anderen $\tau$–Werte ist $h(\tau, t) = 0$.

Gesucht ist die zweidimensionale Übertragungsfunktion $H(f, t)$ als die Fouriertransformierte von $h(\tau, t)$ hinsichtlich der Verzögerungszeit $\tau$:

$$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Mehrwegeempfang beim Mobilfunk.
• Eine ähnliche Problematik wird in der Aufgabe A2.5 behandelt, allerdings mit veränderter Nomenklatur.

Fragebogen

1

Wie groß ist die Periodendauer $T_0$ der Funktion $h(\tau = 1 \ {\rm \mu s}, t)$? Beachten Sie, dass in der Grafik der Betrag $|h(\tau, t)| dargestellt ist.

$T_0 \ = \ $ $\ \rm ms$

2

Zu welchen Zeiten $t_1$ (zwischen $0$ und $10 \ \rm ms$) und $t_2$ (zwischen $10 \ \rm ms$ und $20 \ \rm ms$) ist $H(f, t)$ bezüglich $f$ konstant?

$t_1 \ = \ $ $\ \rm ms$

$t_2 \ = \ $ $\ \rm ms$

3

Berechnen Sie $H_0(f) = H(f, t = 0)$. Welche Aussagen sind zutreffend?

	Es gilt $H_0(f) = H_0(f + i \cdot 1 \ {\rm MHz}), i = ±1, ±2, \ ...$
	Es gilt näherungsweise $0.293 ≤ |H_0(f)| ≤ 1.707$.
	$|H_0(f)|$ hat bei $f = 0$ ein Maximum.

4

Berechnen Sie $H_{10}(f) = H(f, t = 10 \ \rm ms)$. Welche Aussagen sind zutreffend?

	Es gilt $H_{10}(f) = H_{10}(f + i \cdot 1 \ \rm MHz), i = ±1, ±2, \ ..$
	Es gilt näherungsweise $0.293 ≤ (H_{10}(f) ≤ 1.707$.
	$|H_{10}(f)|$ hat bei $f = 0$ ein Maximum.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)