Aufgaben:Aufgabe 1.2Z: 3D–Darstellung von Codes: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 1.2Z: 3D–Darstellung von Codes nach 1.2Z 3D–Darstellung von Codes) |
|||
| Zeile 2: | Zeile 2: | ||
}} | }} | ||
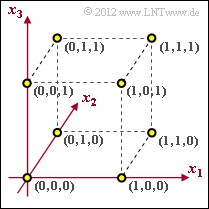
| − | [[Datei:P_ID2400__KC_Z_1_2.png|right|]] | + | [[Datei:P_ID2400__KC_Z_1_2.png|right|frame|Raum $\rm GF(2^3)$ und Code der Länge $n = 3$]] |
| − | Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im | + | Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im $n$–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge $n = 3$: |
| − | :$$\underline{x | + | :$$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$ |
Allgemein gilt bei der Blockcodierung: | Allgemein gilt bei der Blockcodierung: | ||
| − | *Das Informationswort | + | *Das Informationswort $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ wird eindeutig in das Codewort $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ überführt. |
| − | *Die Coderate beträgt R = k/n. | + | *Die Coderate beträgt $R = k/n$. |
| − | *Die Hamming–Distanz $d_{\rm H} | + | *Die Hamming–Distanz $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ zwischen zwei Codeworten $x ∈ \mathcal{}C$ und $x\hspace{0.05cm}' ∈ \mathcal{}C$ gibt die Anzahl der Bitpositionen an, in denen sich $x$ und $x\hspace{0.05cm}'$ unterscheiden. |
| − | *Die Minimaldistanz $d_{\rm min} | + | *Die Minimaldistanz $d_{\rm min} = {\rm min}[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')]$ ist ein Maß für die Korrekturfähigkeit eines Codes. |
| − | *Es können | + | *Es können $e =d_{\rm min} – 1$ Fehler erkannt und $t =(d_{\rm min} – 1)/2$ Fehler korrigiert werden. Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$. |
| + | |||
| + | |||
| + | |||
| + | ''Hinweise'': | ||
| + | *Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Zielsetzung_der_Kanalcodierung|Zielsetzung der Kanalcodierung]]. | ||
| + | *Zusätzlich werden einige einfache Fragen zum Kapitel [[Kanalcodierung/Beispiele_binärer_Blockcodes|Beispiele binärer Blockcodes]] vorweg genommen. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 20: | Zeile 26: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Aussagen gelten, wenn alle Punkte in GF( | + | {Welche Aussagen gelten, wenn alle Punkte in $\rm GF(2^3)$ belegt sind? |
|type="[]"} | |type="[]"} | ||
| − | + Es gilt die Zuordnung | + | + Es gilt die Zuordnung $\underline{u} = (u_{1}, u_{2}, u_{3})$ → $\underline{u} = (x_{1}, x_{2},x_{3})$. |
| − | - Es gilt die Identität | + | - Es gilt die Identität $\underline{x} = \underline{u}$. |
| − | + Die Coderate ist R = 1. | + | + Die Coderate ist $R = 1$. |
| − | -Die Minimaldistanz zwischen zwei Codeworten ist $d_{\rm min} | + | -Die Minimaldistanz zwischen zwei Codeworten ist $d_{\rm min} = 2$. |
{Welche Aussagen gelten für einen (3, 2, 2)–Blockcode? | {Welche Aussagen gelten für einen (3, 2, 2)–Blockcode? | ||
|type="[]"} | |type="[]"} | ||
| − | + Code $ | + | + Code $\mathcal{C}_{1} = \{(0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0)\}$ ist möglich. |
| − | - Code $ | + | - Code $\mathcal{C}_{2} = \{(0, 0, 1), (0, 1, 0), (1, 0, 0), (1, 1, 1)\}$ ist möglich. |
| − | + Code $ | + | + Code $\mathcal{C}_{3} = \{(0, 0, 0), (0, 1, 1), (1, 0, 0), (1, 1, 1)\}$ ist möglich. |
| − | {Welche Eigenschaften zeigt der in Teilaufgabe 2) definierte Code $ | + | {Welche Eigenschaften zeigt der in Teilaufgabe (2) definierte Code $\mathcal{C}_{1}$? |
|type="[]"} | |type="[]"} | ||
+ Ein Bitfehler lässt sich erkennen. | + Ein Bitfehler lässt sich erkennen. | ||
- Ein Bitfehler kann korrigiert werden. | - Ein Bitfehler kann korrigiert werden. | ||
| − | {Welche Eigenschaften zeigt der Code $ | + | {Welche Eigenschaften zeigt der Code $\mathcal{C}_{4}= \{(0, 0, 0), (1, 1, 1)\}$? |
|type="[]"} | |type="[]"} | ||
| − | - Die Coderate beträgt R = 1/4. | + | - Die Coderate beträgt $R = 1/4$. |
| − | + Die Coderate beträgt R = 1/3. | + | + Die Coderate beträgt $R = 1/3$. |
+ Ein Bitfehler lässt sich erkennen. | + Ein Bitfehler lässt sich erkennen. | ||
| − | + | + Ein Bitfehler kann korrigiert werden. | |
| − | |||
| − | |||
| − | |||
| − | |||
Version vom 29. November 2017, 14:07 Uhr
Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im $n$–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge $n = 3$:
- $$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$
Allgemein gilt bei der Blockcodierung:
- Das Informationswort $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ wird eindeutig in das Codewort $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ überführt.
- Die Coderate beträgt $R = k/n$.
- Die Hamming–Distanz $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ zwischen zwei Codeworten $x ∈ \mathcal{}C$ und $x\hspace{0.05cm}' ∈ \mathcal{}C$ gibt die Anzahl der Bitpositionen an, in denen sich $x$ und $x\hspace{0.05cm}'$ unterscheiden.
- Die Minimaldistanz $d_{\rm min} = {\rm min}[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')]$ ist ein Maß für die Korrekturfähigkeit eines Codes.
- Es können $e =d_{\rm min} – 1$ Fehler erkannt und $t =(d_{\rm min} – 1)/2$ Fehler korrigiert werden. Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zielsetzung der Kanalcodierung.
- Zusätzlich werden einige einfache Fragen zum Kapitel Beispiele binärer Blockcodes vorweg genommen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
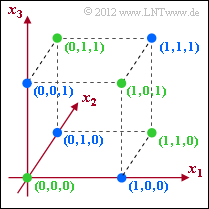
$C_{1}$ und $C_{2}$ beschreiben tatsächlich Codes mit der Rate R = 2/3 und der Minimaldistanz $d_{\rm min}$ = 2 ⇒ Antwort 1 und 2.
In nebenstehender Grafik markieren die grünen Punkte den Code $C_{1}$ und die blauen Punkte den Code $C_{2}$. Beim angegebenen Code $C_{3}$ – ebenfalls mit Rate R = 2/3 – ist die minimale Distanz zwischen zwei Codeworten $d_{\rm min}$ = 1, zum Beispiel zwischen (0, 0, 0) und (1, 0, 0) oder auch zwischen (0, 1, 1) und (1, 1, 1).
(3) Mit der Minimaldistanz $d_{\rm min}$ = 2 kann lediglich ein Bitfehler erkannt werden. In der oberen Grafik kennzeichnen die grünen Punkte zulässige Codeworte von $C_{1}$. Wird ein blauer Punkt empfangen, so weist dies auf einen Übertragungsfehler hin. Eine Fehlerkorrektur ist mit $d_{\rm min}$ = 2 dagegen nicht möglich ⇒ Antwort 1. Hinweis: Der Code $C_{1}$ entspricht dem Single Parity–check Code (3, 2, 2).
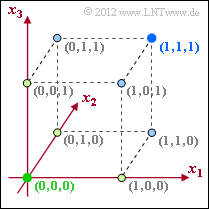
$C_{4}$ beschreibt den (3, 1, 3)–Wiederholungscode. Bei diesem Code sind zwar zwei der insgesamt acht möglichen Punkte belegt, woraus man fälschlicherweise auf die Coderate R = 1/4 schließen könnte. Die Coderate berechnet sich aber gemäß R = k/n = 1/3. Aus der unteren Grafik erkennt man, dass wegen dmin = 3 nun auch ein Bitfehler korrigiert werden kann. Bei der Decodierung werden alle hellgrünen Punkte (mit schwarzer Umrahmung) in den grünen Punkt (0, 0, 0) überführt und alle hellblauen in den blauen Punkt (1, 1, 1). Gleichzeitig können bis zu zwei Bitfehler erkannt werden (einer natürlich auch) ⇒ Richtig sind die Antworten 2, 3 und 4.