Signaldarstellung/Faltungssatz und Faltungsoperation: Unterschied zwischen den Versionen
| Zeile 101: | Zeile 101: | ||
Für die Beschreibungen auf dieser Seite wird von folgender Faltungsoperation ausgegangen: | Für die Beschreibungen auf dieser Seite wird von folgender Faltungsoperation ausgegangen: | ||
| − | $$y(t) = x_1 (t) * x_2 (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | + | :$$y(t) = x_1 (t) * x_2 (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ |
| − | Die Lösung des Faltungsintegrals soll auf grafischem Wege erfolgen. | + | Die Lösung des Faltungsintegrals soll auf grafischem Wege erfolgen. Es wird vorausgesetzt, dass $x_1(t)$ und $x_2(t)$ zeitkontinuierliche Signale sind. |
| − | #Die '''Zeitvariablen''' der beiden Funktionen '''ändern''': $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. | + | |
| − | #Zweite '''Funktion spiegeln''': $x_2(\tau) \to x_2(-\tau)$. | + | Dann sind die folgenden Schritte erforderlich: |
| − | #Gespiegelte '''Funktion''' um $t$ '''verschieben''': $x_2(-\tau) \to x_2(t-\tau)$. | + | |
| − | #'''Multiplikation''' der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$. | + | # Die '''Zeitvariablen''' der beiden Funktionen '''ändern''': $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. |
| − | #'''Integration''' über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$. | + | # Zweite '''Funktion spiegeln''': $x_2(\tau) \to x_2(-\tau)$. |
| + | # Gespiegelte '''Funktion''' um $t$ '''verschieben''': $x_2(-\tau) \to x_2(t-\tau)$. | ||
| + | # '''Multiplikation''' der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$. | ||
| + | # '''Integration''' über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$. | ||
Da die Faltung kommutativ ist, kann anstelle von $x_2(\tau)$ auch $x_1(\tau)$ gespiegelt werden. | Da die Faltung kommutativ ist, kann anstelle von $x_2(\tau)$ auch $x_1(\tau)$ gespiegelt werden. | ||
| − | |||
| − | |||
| − | |||
| + | [[Datei:P_ID2723__Sig_T_3_4_programm.png|right|frame|Bildschirmabzug des Programms „Grafische Faltung”]] | ||
| + | Die Thematik dieses Abschnitts wird auch durch das Interaktionsmodul [[Applets:Graphische_Faltung|Zur Verdeutlichung der grafischen Faltung]] veranschaulicht. Nebenstehende Grafik zeigt einen Bildschirmabzug. | ||
| + | <br clear=all> | ||
| + | [[Datei:P_ID582__Sig_T_3_4_S4_neu.png|right|frame|Beispiel einer Faltungsoperation: <br>Sprungfunktion gefaltet mit Exponentialfunktion]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ | ||
| + | Nun wird die Vorgehensweise anhand eines ausführlichen Beispiels erklärt: | ||
| + | *Am Eingang eines Filters liege eine Sprungfunktion $x(t) = \gamma(t)$ an. | ||
| + | *Die Impulsantwort des RC-Tiefpasses sei $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Die Grafik zeigt rot das Eingangssignal $x(\tau)$, blau die Impulsantwort $h(\tau)$ und grau das Ausgangssignal $y(\tau)$. | Die Grafik zeigt rot das Eingangssignal $x(\tau)$, blau die Impulsantwort $h(\tau)$ und grau das Ausgangssignal $y(\tau)$. | ||
Die Zeitachse ist bereits in $\tau$ umbenannt. | Die Zeitachse ist bereits in $\tau$ umbenannt. | ||
| − | Das Ausgangssignal | + | |
| + | Das Ausgangssignal kann zum Beispiel nach folgender Gleichung berechnet werden: | ||
| − | $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | + | :$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ |
Noch einige Anmerkungen zur grafischen Faltung: | Noch einige Anmerkungen zur grafischen Faltung: | ||
| − | *Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert. | + | *Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal $x(\tau)$ spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert. |
| − | *Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich | + | *Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich Null ist, folgt daraus $y(t=0)=0$. |
| − | *Für jeden anderen Zeitpunkt t muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$. | + | *Für jeden anderen Zeitpunkt t muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$. |
| − | *Da auch $x(t-\tau)$ nur die Werte 0 oder 1 annehmen kann, wird die Integration (allgemein von $\tau_1$ bis $\tau_2$) sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$: | + | *Da in diesem Beispiel auch $x(t-\tau)$ nur die Werte $0$ oder $1$ annehmen kann, wird die Integration (allgemein von $\tau_1$ bis $\tau_2$) sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$: |
| − | $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | + | :$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ |
| − | |||
| − | |||
| − | { | + | Die Skizze gilt für $t=T$ und führt zum Ausgangswert $y(t=T) = 1 – 1/\text{e} \approx 0.632$.}} |
Version vom 17. Januar 2018, 18:23 Uhr
Inhaltsverzeichnis
Faltung im Zeitbereich
Der Faltungssatz ist mit das wichtigste Gesetz der Fouriertransformation, dem in vorliegendem Tutorial ein eigenes Unterkapitel gewidmet wird.
Wir betrachten zunächst den Faltungssatz im Zeitbereich und setzen voraus, dass die Spektren zweier Zeitfunktionen $x_1(t)$ und $x_2(t)$ bekannt sind:
- $$X_1 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$
Dann gilt für die Zeitfunktion des Produktes $X_1(f) \cdot X_2(f)$:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Hierbei ist $\tau$ eine formale Integrationsvariable mit der Dimension einer Zeit.
$\text{Definition:}$ Die obige Verknüpfung der Zeitfunktion $x_1(t)$ und $x_2(t)$ bezeichnet man als Faltung und stellt diesen Funktionalzusammenhang mit einem Stern dar:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$
Damit lässt sich obige Fourierkorrespondenz auch wie folgt schreiben:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
Der Beweis folgt am Kapitelende.
Anmerkung: Die Faltung ist kommutativ ⇒ Die Reihenfolge der Operanden ist vertauschbar: ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t ) $.
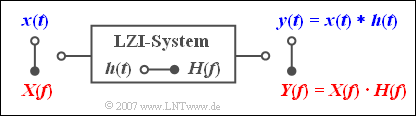
$\text{Beispiel 1:}$ Ein jedes lineare zeitinvariante (LZI-) System kann sowohl durch den Frequenzgang $H(f)$ als auch durch die Impulsantwort $h(t)$ beschrieben werden, wobei der Zusammenhang zwischen diesen beiden Systemgrößen ebenfalls durch die Fouriertransformation gegeben ist.
Legt man an den Eingang ein Signal $x(t)$ mit dem Spektrum $X(f)$ an, so gilt für das Spektrum des Ausgangssignals:
- $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$
Mit dem Faltungssatz ist es nun möglich, das Ausgangssignal auch direkt im Zeitbereich zu berechnen:
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$
Aus dieser Gleichung geht nochmals hervor, dass die Faltungsoperation kommutativ ist.
Faltung im Frequenzbereich
Die Dualität zwischen Zeit– und Frequenzbereich erlaubt auch Aussagen hinsichtlich des Spektrums des Produktsignals:
- $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$
Dieses Resultat lässt sich ähnlich wie der Faltungssatz im Zeitbereich beweisen. Die Integrationsvariable $\nu$ hat aber nun die Dimension einer Frequenz.
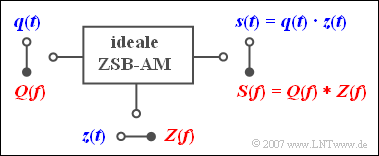
$\text{Beispiel 2:}$ Die Zweiseitenband-Amplitudenmodulation (ZSB-AM) ohne Träger wird durch das skizzierte Modell beschrieben.
- Bei der Zeitbereichsdarstellung (blau) ergibt sich das modulierte Signal $s(t)$ als das Produkt aus dem Nachrichtensignal $q(t)$ und dem (normierten) Trägersignal $z(t)$.
- Nach dem Faltungssatz folgt daraus für den Frequenzbereich (rot), dass das Ausgangsspektrum $S(f)$ gleich dem Faltungsprodukt aus $Q(f)$ und $Z(f)$ ist.
Faltung einer Funktion mit einer Diracfunktion
Sehr einfach wird die Faltungsoperation, wenn einer der beiden Operanden eine Diracfunktion ist. Dies gilt für die Faltung im Zeit– und im Frequenzbereich gleichermaßen.
Wir betrachten beispielhaft die Faltung einer Funktion $x_1(t)$ mit der Funktion
- $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T}.$$
Für die Spektralfunktion des Signals $y(t) = x_1(t) \ast x_2(t)$ gilt dann:
- $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T} .$$
Die komplexe Exponentialfunktion führt zu einer Verschiebung um $T$ ⇒ Verschiebungssatz, der Faktor $\alpha$ zu einer Dämpfung ($\alpha < 1$) bzw. Verstärkung ($\alpha > 1$ ). Daraus folgt:
- $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$
$\text{In Worten: }$ Die Faltung einer beliebigen Funktion mit einer Diracfunktion bei $t = T$ ergibt die um $T$ nach rechts verschobene Funktion, wobei noch die Gewichtung der Diracfunktion durch den Faktor $\alpha$ zu berücksichtigen ist.
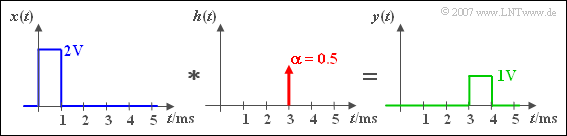
$\text{Beispiel 3:}$ Ein Rechtecksignal $x(t)$ wird durch ein LZI-System um eine Laufzeit $\tau = 3\,\text{ ms}$ verzögert und um den Faktor $\alpha = 0.5$ gedämpft.
Die Verschiebung und die Dämpfung erkennt man sowohl am Ausgangssignal $y(t)$ als auch an der Impulsantwort $h(t)$.
Grafische Faltung
Für die Beschreibungen auf dieser Seite wird von folgender Faltungsoperation ausgegangen:
- $$y(t) = x_1 (t) * x_2 (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Die Lösung des Faltungsintegrals soll auf grafischem Wege erfolgen. Es wird vorausgesetzt, dass $x_1(t)$ und $x_2(t)$ zeitkontinuierliche Signale sind.
Dann sind die folgenden Schritte erforderlich:
- Die Zeitvariablen der beiden Funktionen ändern: $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$.
- Zweite Funktion spiegeln: $x_2(\tau) \to x_2(-\tau)$.
- Gespiegelte Funktion um $t$ verschieben: $x_2(-\tau) \to x_2(t-\tau)$.
- Multiplikation der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$.
- Integration über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$.
Da die Faltung kommutativ ist, kann anstelle von $x_2(\tau)$ auch $x_1(\tau)$ gespiegelt werden.
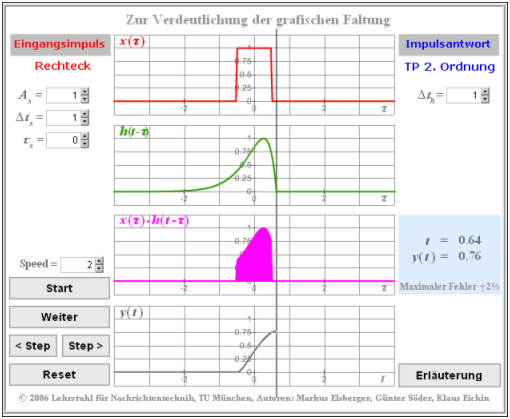
Die Thematik dieses Abschnitts wird auch durch das Interaktionsmodul Zur Verdeutlichung der grafischen Faltung veranschaulicht. Nebenstehende Grafik zeigt einen Bildschirmabzug.
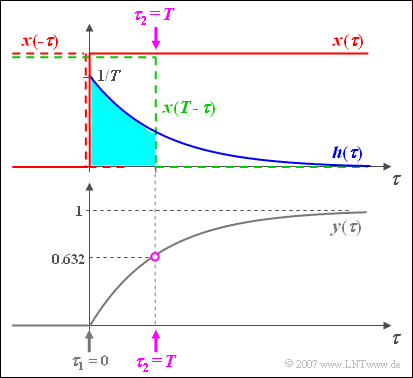
$\text{Beispiel 4:}$ Nun wird die Vorgehensweise anhand eines ausführlichen Beispiels erklärt:
- Am Eingang eines Filters liege eine Sprungfunktion $x(t) = \gamma(t)$ an.
- Die Impulsantwort des RC-Tiefpasses sei $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$
Die Grafik zeigt rot das Eingangssignal $x(\tau)$, blau die Impulsantwort $h(\tau)$ und grau das Ausgangssignal $y(\tau)$.
Die Zeitachse ist bereits in $\tau$ umbenannt.
Das Ausgangssignal kann zum Beispiel nach folgender Gleichung berechnet werden:
- $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Noch einige Anmerkungen zur grafischen Faltung:
- Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal $x(\tau)$ spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert.
- Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich Null ist, folgt daraus $y(t=0)=0$.
- Für jeden anderen Zeitpunkt t muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$.
- Da in diesem Beispiel auch $x(t-\tau)$ nur die Werte $0$ oder $1$ annehmen kann, wird die Integration (allgemein von $\tau_1$ bis $\tau_2$) sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$:
- $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$
Die Skizze gilt für $t=T$ und führt zum Ausgangswert $y(t=T) = 1 – 1/\text{e} \approx 0.632$.
Anschauliche Deutung der Faltung
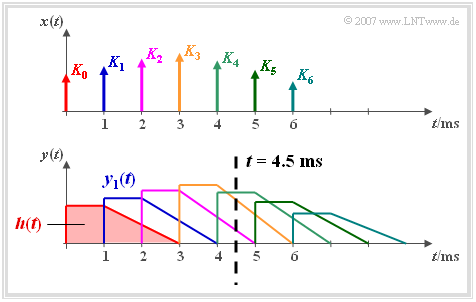
Wir gehen von einem Tiefpassfilter mit der Impulsantwort $h(t)$ aus, die zunächst eine Millisekunde lang konstant ist und dann bis zur Zeit $t = 3 \,\text{ms}$ linear abfällt.
- Legt man an den Eingang dieses Filters einen Diracimpuls $K_0 \cdot \delta(t)$ an, so ist das Ausgangssignal $y(t)$ formgleich mit der Impulsantwort $h(t)$. Der Sachverhalt ist im Bild rot dargestellt.
- Ein um $T= 1 \,\text{ms}$ späterer Diracimpuls mit Gewicht $K_1 > K_0$ hat das blau gezeichnete Ausgangssignal $y_1(t)$ zur Folge, das gegenüber dem roten Signal verzögert und in der Amplitude vergrößert ist.
Wir betrachten nun das aus sieben verschieden gewichteten und verschobenen Diracimpulsen bestehende Eingangssignal
$$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$
das als zeitdiskrete Näherung eines zeitkontinuierlichen Signals aufgefasst werden kann.
Das Signal am Ausgang des linearen Systems ist die Summe der sieben im Bild verschiedenfarbig markierten Teilsignale:
$$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$
Betrachten wir nun beispielhaft den Signalwert zum Zeitpunkt $t = 4.5T$ (siehe Strichpunktierung):
$$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$
Der Signalwert $y(4.5T)$ wird somit nur durch die Eingangssignalwerte $K_2$, $K_3$ und $K_4$ bestimmt, und zwar ist der Einfluss
- von $K_4$ wegen $h(0.5T) = 1$ am stärksten,
- von $K_3$ wegen $h(1.5T) = 0.75$ weniger stark,
- von $K_2$ wegen $h(2.5T) = 0.25$ am geringsten.
Beweis des Faltungssatzes
Man bezeichnet die folgende Verknüpfung der Zeitfunktionen $x_1(t)$ und $x_2(t)$ als Faltung und stellt diesen Funktionalzusammenhang mit einem Stern dar:
$$x_{\rm{1}} (t) * x_{\rm{2}} (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
Daraus ergibt sich die folgende Fourierkorrespondenz:
$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ).$$
Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen:
$$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}f\tau }\hspace{0.1cm} {\rm{d }}\tau{\rm{,}}$$
$$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} )} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}ft'}\hspace{0.1cm} {\rm{d}}t'{\rm{.}}$$
Bildet man das Produkt der Spektralfunktionen, so erhält man:
$$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t'} ) \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}f\left( {\tau + t'} \right)}\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t'{\rm{.}}$$
Mit der Substitution $t = \tau + t'$ ergibt sich:
$$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d }}}\tau \right]} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}ft}\hspace{0.1cm} {\rm{d}}t{\rm{.}}$$
In dieser Gleichung ist bereits berücksichtigt, dass die Exponentialfunktion unabhängig von der inneren Integrationsvariablen $τ$ ist und deshalb nur als Faktor des inneren Integrals fungiert.
Bezeichnen wir nun das Produkt der beiden Spektren mit $P(f)$ und die dazugehörige Zeitfunktion mit $p(t)$, so lautet das entsprechende Fourierintegral:
$$P(f) = \int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}ft} \hspace{0.1cm}{\rm{d}}t{\rm{.}}$$
Ein Koeffizientenvergleich der beiden Integrale zeigt, dass folgender Zusammenhang gilt:
$$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d }}\tau{\rm{.}}$$
Aufgaben zum Kapitel
A3.9 Faltung von Rechteck und Gauß