Digitalsignalübertragung/Lineare Nyquistentzerrung: Unterschied zwischen den Versionen
| Zeile 11: | Zeile 11: | ||
[[Datei:P ID1423 Dig T 3 5 S1 version1.png|center|frame|Blockschaltbild des optimalen Nyquistentzerrers|class=fit]] | [[Datei:P ID1423 Dig T 3 5 S1 version1.png|center|frame|Blockschaltbild des optimalen Nyquistentzerrers|class=fit]] | ||
| − | |||
Hierzu ist anzumerken: | Hierzu ist anzumerken: | ||
| − | *Die Diracquelle liefert die zu übertragende Nachricht in binärer bipolarer Form ⇒ Amplitudenkoeffizienten $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. Sie wird als redundanzfrei vorausgesetzt.<br> | + | *Die ''Diracquelle'' liefert die zu übertragende Nachricht in binärer bipolarer Form ⇒ Amplitudenkoeffizienten $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. Sie wird als redundanzfrei vorausgesetzt.<br> |
| − | *Die Sendeimpulsform $g_s(t)$ wird durch den Senderfrequenzgang $H_{\rm S}(f)$ berücksichtigt. Bei allen Beispielen ist $H_{\rm S}(f) = {\rm si}(\pi f T)$ zugrunde gelegt ⇒ NRZ–Rechteck–Sendeimpulse .<br> | + | *Die ''Sendeimpulsform'' $g_s(t)$ wird durch den Senderfrequenzgang $H_{\rm S}(f)$ berücksichtigt. Bei allen Beispielen ist $H_{\rm S}(f) = {\rm si}(\pi f T)$ zugrunde gelegt ⇒ NRZ–Rechteck–Sendeimpulse .<br> |
| − | *Bei manchen Herleitungen werden Sender und Kanal – hierfür wird meist ein Koaxialkabel angenommen – durch den gemeinsamen Frequenzgang $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ zusammengefasst.<br> | + | *Bei manchen Herleitungen werden Sender und Kanal – hierfür wird meist ein Koaxialkabel angenommen – durch den ''gemeinsamen Frequenzgang'' $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ zusammengefasst.<br> |
*Das Empfangsfilter $H_{\rm E}(f)$ setzt sich multiplikativ aus dem [[Stochastische_Signaltheorie/Matched-Filter|Matched–Filter]] $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ und dem [[Digitalsignalübertragung/Lineare_Nyquistentzerrung#Wirkungsweise_des_Transversalfilters|Transversalfilter]] $H_{\rm TF}(f)$ zusammen, zumindest kann es gedanklich so aufgespalten werden. | *Das Empfangsfilter $H_{\rm E}(f)$ setzt sich multiplikativ aus dem [[Stochastische_Signaltheorie/Matched-Filter|Matched–Filter]] $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ und dem [[Digitalsignalübertragung/Lineare_Nyquistentzerrung#Wirkungsweise_des_Transversalfilters|Transversalfilter]] $H_{\rm TF}(f)$ zusammen, zumindest kann es gedanklich so aufgespalten werden. | ||
| Zeile 26: | Zeile 25: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Mit dieser Bedingung ergibt sich die maximale Augenöffnung (keine Impulsinterferenzen). Deshalb gelten für das Detektions–SNR und den Systemwirkungsgrad bei binärer Signalisierung: | + | *Mit dieser Bedingung ergibt sich die maximale Augenöffnung (keine Impulsinterferenzen). Deshalb gelten für das [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter|Detektions–SNR]] und den [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme#Systemoptimierung_bei_Spitzenwertbegrenzung|Systemwirkungsgrad]] bei binärer Signalisierung: |
:$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | :$$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Zeile 58: | Zeile 57: | ||
| − | Für den Eingangsimpuls $g_m(t)$ setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, | + | Für den Eingangsimpuls $g_m(t)$ setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser |
| − | * | + | *symmetrisch um $t=0$ ist (Ausgang des Matched–Filters),<br> |
| − | * | + | *zu den Zeiten $\nu \cdot T$ und $-\nu \cdot T$ jeweils den Wert $g_m(\nu)$ besitzt.<br> |
| − | Damit | + | Damit lauten die Eingangsimpulswerte: |
:$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | :$$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | ||
{0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | ||
\text{...}\hspace{0.05cm}.$$ | \text{...}\hspace{0.05cm}.$$ | ||
| − | Für den Detektionsgrundimpuls $g_d(t)$ am Filterausgang ergeben sich demzufolge zu den Zeitpunkten $\nu \cdot T$ mit den Abkürzungen $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$ folgende Werte: | + | Für den Detektionsgrundimpuls $g_d(t)$ am Filterausgang ergeben sich demzufolge zu den Zeitpunkten $\nu \cdot T$ mit den Abkürzungen $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$ folgende Werte: |
:$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | :$$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | ||
\cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$ | ||
:$$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 | :$$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 | ||
| − | \cdot [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3)], $$ | + | \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$ |
:$$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 | :$$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 | ||
| − | \cdot [g_m(1)+g_m(3)]+ k_2 \cdot [g_m(2)+g_m(4)] | + | \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| Zeile 84: | Zeile 83: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Wir gehen von dem symmetrischen Eingangssignal entsprechend dem oberen Diagramm aus. Mit der Abkürzung $g_m(\nu)= g_m(\pm \nu \cdot T)$ gibt es folgende Abtastwerte im Abstand der Symboldauer $T$: | + | $\text{Beispiel 1:}$ Wir gehen von dem symmetrischen Eingangssignal entsprechend dem oberen Diagramm in der Grafik aus. Mit der Abkürzung $g_m(\nu)= g_m(\pm \nu \cdot T)$ gibt es folgende Abtastwerte im Abstand der Symboldauer $T$: |
:$$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} | :$$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= | \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= | ||
| Zeile 90: | Zeile 89: | ||
\hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$ | ||
| − | Für den Ausgangsimpuls soll $g_d(t =0) = 1$ und $g_d(t =\pm T) = 0$gelten. Hierzu eignet sich ein Laufzeitfilter erster Ordnung mit den Koeffizienten $ | + | Für den Ausgangsimpuls soll $g_d(t =0) = 1$ und $g_d(t =\pm T) = 0$ gelten. Hierzu eignet sich ein Laufzeitfilter erster Ordnung mit den Koeffizienten $k_0$ und $k_1$, die folgende Bedingungen erfüllen müssen: |
[[Datei:P ID1425 Dig T 3 5 S2b version1.png|right|frame|Eingangs- und Ausgangsimpuls des optimalen Nyquistentzerrers]] | [[Datei:P ID1425 Dig T 3 5 S2b version1.png|right|frame|Eingangs- und Ausgangsimpuls des optimalen Nyquistentzerrers]] | ||
:$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | :$$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
| − | [1.000 +0.135] = 0\hspace{0.3cm}\Rightarrow | + | \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow |
\hspace{0.3cm}{k_1} = | \hspace{0.3cm}{k_1} = | ||
-0.214 \cdot {k_0}\hspace{0.05cm},$$ | -0.214 \cdot {k_0}\hspace{0.05cm},$$ | ||
| Zeile 103: | Zeile 102: | ||
*Das mittlere Diagramm zeigt, dass damit der erste Vorläufer und der erste Nachläufer kompensiert werden können und zugleich $g_d(0) =1$ gilt (gelbe Hinterlegung). | *Das mittlere Diagramm zeigt, dass damit der erste Vorläufer und der erste Nachläufer kompensiert werden können und zugleich $g_d(0) =1$ gilt (gelbe Hinterlegung). | ||
*Die weiteren Detektionsgrundimpulswerte (blaue Kreise) sind aber von Null verschieden und bewirken Impulsinterferenzen.<br><br> | *Die weiteren Detektionsgrundimpulswerte (blaue Kreise) sind aber von Null verschieden und bewirken Impulsinterferenzen.<br><br> | ||
| − | |||
Das untere Diagramm zeigt, dass mit einem Filter zweiter Ordnung $(N = 2)$ Nulldurchgänge bei $\pm T$ und bei $\pm 2T$ erzwungen werden, wenn die Koeffizienten $k_0 = 1.127$, $k_1 = 0.219$ und $k_2 = 0.075$ geeignet gewählt sind. Das Gleichungssystem zur Bestimmung der optimalen Koeffizienten lautet dabei: | Das untere Diagramm zeigt, dass mit einem Filter zweiter Ordnung $(N = 2)$ Nulldurchgänge bei $\pm T$ und bei $\pm 2T$ erzwungen werden, wenn die Koeffizienten $k_0 = 1.127$, $k_1 = 0.219$ und $k_2 = 0.075$ geeignet gewählt sind. Das Gleichungssystem zur Bestimmung der optimalen Koeffizienten lautet dabei: | ||
| Zeile 109: | Zeile 107: | ||
\cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$ | ||
:$$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | :$$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot | ||
| − | [1.000+0.135]+ k_2 \cdot [0.243+0.086] = 0\hspace{0.05cm},$$ | + | \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$ |
:$$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot | :$$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot | ||
| − | [0.243+0.086]+ k_2 \cdot [1.000 + 0.059]= 0 \hspace{0.05cm}.$$}}<br> | + | \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$}}<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ Die Ergebnisse können wie folgt verallgemeinert werden: | $\text{Fazit:}$ Die Ergebnisse können wie folgt verallgemeinert werden: | ||
| − | *Mit einem Laufzeitfilter $N$–ter Ordnung können der Hauptwert $g_d(0)$ zu Eins (normiert) sowie die ersten $N$ Nachläufer $g_{\nu}$ und die ersten $N$ $g_{-\nu}$ | + | *Mit einem Laufzeitfilter $N$–ter Ordnung können der Hauptwert $g_d(0)$ zu Eins (normiert) sowie die ersten $N$ Nachläufer $g_{\nu}$ und die ersten $N$ Vorläufer $g_{-\nu}$ zu Null gemacht werden.<br> |
| − | *Weitere Vor– und Nachläufer $ | + | *Weitere Vor– und Nachläufer $(\nu \gt N)$ lassen sich so nicht kompensieren. Es ist sogar möglich, dass die Vor– und Nachläufer außerhalb des Kompensationsbereichs vergrößert werden oder sogar neu entstehen.<br> |
| − | *Im Grenzübergang $N \to \infty$ (in der Praxis heißt das: ein Filter mit sehr vielen Koeffizienten) ist eine vollständige Nyquistentzerrung und damit eine impulsinterferenzfreie Übertragung möglich.}} | + | *Im Grenzübergang $N \to \infty$ (in der Praxis heißt das: ein Filter mit sehr vielen Koeffizienten) ist eine vollständige Nyquistentzerrung und damit eine impulsinterferenzfreie Übertragung möglich.}} |
| Zeile 125: | Zeile 123: | ||
<br> | <br> | ||
Die Tatsache, dass sich der optimale Nyquistentzerrer multiplikativ aus | Die Tatsache, dass sich der optimale Nyquistentzerrer multiplikativ aus | ||
| − | *dem Matched–Filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – also angepasst an den Empfangsgrundimpuls –<br> | + | *dem Matched–Filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – also angepasst an den Empfangsgrundimpuls $g_e(t)$ – und<br> |
| − | * | + | *einem Transversalfilter $H_{\rm MF}(f) $ mit unendlich vielen Filterkoeffizienten<br><br> |
zusammensetzt, folgt aus dem ersten Nyquistkriterium. Durch Anwendung der [https://de.wikipedia.org/wiki/Variationsrechnung Variationsrechnung] erhält man den Frequenzgang des Transversalfilters – siehe [ST85]<ref name='ST85'> Söder, G.; Tröndle, K.: ''Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme.'' Berlin – Heidelberg: Springer, 1985.</ref>: | zusammensetzt, folgt aus dem ersten Nyquistkriterium. Durch Anwendung der [https://de.wikipedia.org/wiki/Variationsrechnung Variationsrechnung] erhält man den Frequenzgang des Transversalfilters – siehe [ST85]<ref name='ST85'> Söder, G.; Tröndle, K.: ''Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme.'' Berlin – Heidelberg: Springer, 1985.</ref>: | ||
| Zeile 134: | Zeile 132: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die linke Grafik zeigt den | + | Die linke Grafik zeigt den Funktionsverlauf $20 \cdot \lg \ H_{\rm TF}(f)$ im Bereich $| f | \le 1/T$. Vorausgesetzt sind hierfür rechteckförmige NRZ–Sendeimpulse und ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_\star$. |
| − | [[Datei:Dig_T_3_5_S3b_version2.png|center|frame|Frequenzgang des optimalen Nyquistentzerrers|class=fit]] | + | [[Datei:Dig_T_3_5_S3b_version2.png|center|frame|(Betrags–)Frequenzgang des Transversalfilter und des gesamten optimalen Nyquistentzerrers|class=fit]] |
Man erkennt aus obiger Gleichung und der linken Grafik: | Man erkennt aus obiger Gleichung und der linken Grafik: | ||
| Zeile 152: | Zeile 150: | ||
In der rechten Grafik ist der Frequenzgang $20 \cdot \lg \ |H_{\rm E}(f)|$ des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt: | In der rechten Grafik ist der Frequenzgang $20 \cdot \lg \ |H_{\rm E}(f)|$ des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt: | ||
| − | :$$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{ | + | :$$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - |
{\kappa}/{T}) | {\kappa}/{T}) | ||
|^2}.$$ | |^2}.$$ | ||
| Zeile 160: | Zeile 158: | ||
*Während der Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ bei $a_\star \ne 0 \ \rm dB$ symmetrisch zur Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$ ist, ist diese Symmetrie beim Empfangsfilter–Gesamtfrequenzgang $H_{\rm E}(f)$ nicht mehr gegeben.<br> | *Während der Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ bei $a_\star \ne 0 \ \rm dB$ symmetrisch zur Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$ ist, ist diese Symmetrie beim Empfangsfilter–Gesamtfrequenzgang $H_{\rm E}(f)$ nicht mehr gegeben.<br> | ||
*Die Maxima der Frequenzgänge $H_{\rm TF}(f)$ und $|H_{\rm E}(f)|$ hängen signifikant von der charakteristischen Kabeldämpfung $a_\star$ ab. Aus dem blauen bzw. roten Funktionsverlauf kann abgelesen werden: | *Die Maxima der Frequenzgänge $H_{\rm TF}(f)$ und $|H_{\rm E}(f)|$ hängen signifikant von der charakteristischen Kabeldämpfung $a_\star$ ab. Aus dem blauen bzw. roten Funktionsverlauf kann abgelesen werden: | ||
| − | :$$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}[H_{\rm | + | :$$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm |
| − | TF}(f)]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm | + | TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm |
| − | Max}[\ |H_{\rm E}(f)| \ ] \approx 40\,{\rm dB}\hspace{0.05cm},$$ | + | Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$ |
| − | :$$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}[H_{\rm TF}(f)] | + | :$$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] |
| − | \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}[\ |H_{\rm E}(f)|\ ] | + | \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] |
\approx 80\,{\rm dB}\hspace{0.05cm}.$$ | \approx 80\,{\rm dB}\hspace{0.05cm}.$$ | ||
| Zeile 170: | Zeile 168: | ||
== Approximation des optimalen Nyquistentzerrers == | == Approximation des optimalen Nyquistentzerrers == | ||
<br> | <br> | ||
| − | Betrachten wir nun den Gesamtfrequenzgang zwischen der Diracquelle und dem Entscheider. Dieser setzt sich multiplikativ aus den Frequenzgängen von Sender, Kanal und Empfänger zusammen. Entsprechend der Herleitung muss der Gesamtfrequenzgang die Nyquistbedingung erfüllen: | + | Betrachten wir nun den Gesamtfrequenzgang zwischen der Diracquelle und dem Entscheider. |
| + | *Dieser setzt sich multiplikativ aus den Frequenzgängen von Sender, Kanal und Empfänger zusammen. | ||
| + | *Entsprechend der Herleitung muss der Gesamtfrequenzgang die Nyquistbedingung erfüllen: | ||
| + | |||
:$$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = | :$$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = | ||
\frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
| Zeile 176: | Zeile 177: | ||
|^2}\hspace{0.05cm}.$$ | |^2}\hspace{0.05cm}.$$ | ||
| + | [[Datei:P ID1428 Dig T 3 5 S3c version1.png|right|frame|Optimaler Nyquistfrequenzgang bei einem Koaxialkabel|class=fit]] | ||
Die Grafik zeigt folgende Eigenschaften des ''optimalen Nyquistentzerrers'' (ONE): | Die Grafik zeigt folgende Eigenschaften des ''optimalen Nyquistentzerrers'' (ONE): | ||
| − | *Ist die Kabeldämpfung hinreichend groß $(a_\star \ge 10 \ \rm dB)$, so kann | + | *Ist die Kabeldämpfung hinreichend groß $(a_\star \ge 10 \ \rm dB)$, so kann man den Gesamtfrequenzgang mit guter Näherung durch einen [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#1.2FT.E2.80.93Nyquistspektren| Cosinus–Rolloff–Tiefpass]] beschreiben.<br> |
| + | |||
*Je größer $a_\star$ ist, desto kleiner ist der Rolloff–Faktor $r$ und um so steiler verläuft der Flankenabfall. Für die charakteristische Kabeldämpfung $a_\star = 40 \ \rm dB$ (blaue Kurve) ergibt sich $r \approx 0.4$, für $a_\star = 80 \ \rm dB$ (rote Kurve) $r \approx 0.18$.<br> | *Je größer $a_\star$ ist, desto kleiner ist der Rolloff–Faktor $r$ und um so steiler verläuft der Flankenabfall. Für die charakteristische Kabeldämpfung $a_\star = 40 \ \rm dB$ (blaue Kurve) ergibt sich $r \approx 0.4$, für $a_\star = 80 \ \rm dB$ (rote Kurve) $r \approx 0.18$.<br> | ||
| + | |||
*Oberhalb der Frequenz $f_{\rm Nyq} \cdot (1 + r)$ besitzt $H_{\rm Nyq}(f)$ keine Anteile. Bei idealem Kanal ⇒ $a_\star = 0 \ \rm dB$ (grüne Kurve) reicht $H_{\rm Nyq}(f)= {\rm si}^2(\pi f T)$ allerdings theoretisch bis ins Unendliche. | *Oberhalb der Frequenz $f_{\rm Nyq} \cdot (1 + r)$ besitzt $H_{\rm Nyq}(f)$ keine Anteile. Bei idealem Kanal ⇒ $a_\star = 0 \ \rm dB$ (grüne Kurve) reicht $H_{\rm Nyq}(f)= {\rm si}^2(\pi f T)$ allerdings theoretisch bis ins Unendliche. | ||
| + | <br clear=all> | ||
| + | Das Interaktionsmodul [[Tiefpässe im Frequenz- und Zeitbereich]] verdeutlicht die Eigenschaften des Cosinus–Rolloff–Tiefpasses. | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Berechnung der normierten Störleistung == | == Berechnung der normierten Störleistung == | ||
Version vom 11. Juni 2018, 09:28 Uhr
Inhaltsverzeichnis
Struktur des optimalen Nyquistentzerrers
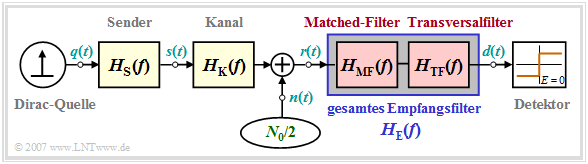
In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems aus.
Hierzu ist anzumerken:
- Die Diracquelle liefert die zu übertragende Nachricht in binärer bipolarer Form ⇒ Amplitudenkoeffizienten $a_\nu \in \{ -1, \hspace{0.05cm}+1\}$. Sie wird als redundanzfrei vorausgesetzt.
- Die Sendeimpulsform $g_s(t)$ wird durch den Senderfrequenzgang $H_{\rm S}(f)$ berücksichtigt. Bei allen Beispielen ist $H_{\rm S}(f) = {\rm si}(\pi f T)$ zugrunde gelegt ⇒ NRZ–Rechteck–Sendeimpulse .
- Bei manchen Herleitungen werden Sender und Kanal – hierfür wird meist ein Koaxialkabel angenommen – durch den gemeinsamen Frequenzgang $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ zusammengefasst.
- Das Empfangsfilter $H_{\rm E}(f)$ setzt sich multiplikativ aus dem Matched–Filter $H_{\rm MF}(f) = H_{\rm SK}^\star(f)$ und dem Transversalfilter $H_{\rm TF}(f)$ zusammen, zumindest kann es gedanklich so aufgespalten werden.
- Der Gesamtfrequenzgang zwischen Diracquelle und Schwellenwertentscheider soll die erste Nyquistbedingung erfüllen. Es muss also gelten:
- $$H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) = H_{\rm Nyq}(f) \hspace{0.05cm}.$$
- Mit dieser Bedingung ergibt sich die maximale Augenöffnung (keine Impulsinterferenzen). Deshalb gelten für das Detektions–SNR und den Systemwirkungsgrad bei binärer Signalisierung:
- $$\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.05cm}.$$
- Die Optimierungsaufgabe beschränkt sich also darauf, das Empfangsfilter $H_{\rm E}(f)$ so zu bestimmen, dass die normierte Rauschleistung vor dem Entscheider den kleinstmöglichen Wert annimmt:
- \[\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \stackrel {!}{=} {\rm Minimum}\hspace{0.05cm}.\]
$\text{Definition:}$ Wir bezeichnen die hier beschriebene Konfiguration als Optimale Nyquistentzerrung (ONE). Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst $M = 2$.
Wirkungsweise des Transversalfilters
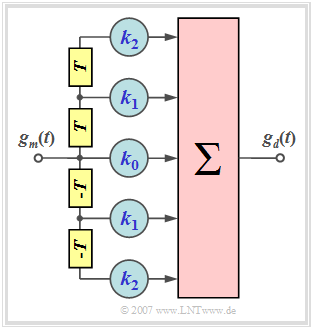
Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters
- $$H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) $$
mit folgenden Eigenschaften:
- $N$ gibt die Ordnung des Filters an ⇒ die Grafik zeigt ein Filter zweiter Ordnung $(N=2)$.
- Für die Filterkoeffizienten gilt $k_{-\lambda} = k_{\lambda}$ ⇒ symmetrische Struktur ⇒ $H_{\rm TF}(f)$ ist reell.
- $H_{\rm TF}(f)$ ist somit durch die Koeffizienten $k_0$, ... , $k_N$ vollständig bestimmt.
Für den Eingangsimpuls $g_m(t)$ setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser
- symmetrisch um $t=0$ ist (Ausgang des Matched–Filters),
- zu den Zeiten $\nu \cdot T$ und $-\nu \cdot T$ jeweils den Wert $g_m(\nu)$ besitzt.
Damit lauten die Eingangsimpulswerte:
- $$\text{...}\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} \text{...}\hspace{0.05cm}.$$
Für den Detektionsgrundimpuls $g_d(t)$ am Filterausgang ergeben sich demzufolge zu den Zeitpunkten $\nu \cdot T$ mit den Abkürzungen $g_0 =g_d(t= 0)$, $g_1 =g_d(t= \pm T)$, $g_2 =g_d(t= \pm 2T)$ folgende Werte:
- $$ t = 0\hspace{-0.1cm}:\hspace{0.9cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} $$
- $$ t = \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot g_m(1) + k_1 \cdot \big [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3) \big ], $$
- $$ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 \cdot \big [g_m(1)+g_m(3)\big ]+ k_2 \cdot \big [g_m(2)+g_m(4)\big ] \hspace{0.05cm}. $$
Aus diesem System mit drei linear unabhängigen Gleichungen kann man nun die Filterkoeffizienten $k_0$, $k_1$ und $k_2$ so bestimmen, dass der Detektionsgrundimpuls $g_d(t)$ folgende Stützstellen aufweist:
- $$\text{...}\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} \text{...}$$
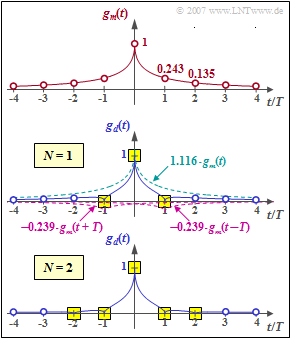
$\text{Beispiel 1:}$ Wir gehen von dem symmetrischen Eingangssignal entsprechend dem oberen Diagramm in der Grafik aus. Mit der Abkürzung $g_m(\nu)= g_m(\pm \nu \cdot T)$ gibt es folgende Abtastwerte im Abstand der Symboldauer $T$:
- $$g_m(t) = {\rm e}^{ - \sqrt{2 \hspace{0.05cm} \cdot \hspace{0.05cm}\vert\hspace{0.05cm} t \hspace{0.05cm} \vert /T} }\hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.35cm}g_m(1)= 0.243,\hspace{0.35cm}g_m(2)= 0.135,\hspace{0.35cm}g_m(3)= 0.086, \hspace{0.35cm}g_m(4)= 0.059 \hspace{0.05cm}.$$
Für den Ausgangsimpuls soll $g_d(t =0) = 1$ und $g_d(t =\pm T) = 0$ gelten. Hierzu eignet sich ein Laufzeitfilter erster Ordnung mit den Koeffizienten $k_0$ und $k_1$, die folgende Bedingungen erfüllen müssen:
- $$t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000 +0.135 \big ] = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{k_1} = -0.214 \cdot {k_0}\hspace{0.05cm},$$
- $$ t = 0 \hspace{-0.1cm} : \hspace{0.6cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243= 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm}0.896 \cdot {k_0} = 1 \hspace{0.05cm}.$$
Daraus erhält man die optimalen Filterkoeffizienten $k_0 = 1.116$ und $k_1 = 0.239$.
- Das mittlere Diagramm zeigt, dass damit der erste Vorläufer und der erste Nachläufer kompensiert werden können und zugleich $g_d(0) =1$ gilt (gelbe Hinterlegung).
- Die weiteren Detektionsgrundimpulswerte (blaue Kreise) sind aber von Null verschieden und bewirken Impulsinterferenzen.
Das untere Diagramm zeigt, dass mit einem Filter zweiter Ordnung $(N = 2)$ Nulldurchgänge bei $\pm T$ und bei $\pm 2T$ erzwungen werden, wenn die Koeffizienten $k_0 = 1.127$, $k_1 = 0.219$ und $k_2 = 0.075$ geeignet gewählt sind. Das Gleichungssystem zur Bestimmung der optimalen Koeffizienten lautet dabei:
- $$t = 0\hspace{-0.1cm}:\hspace{0.85cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},$$
- $$t= \pm T\hspace{-0.1cm}:\hspace{0.45cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot \big [1.000+0.135 \big ]+ k_2 \cdot \big [0.243+0.086 \big ] = 0\hspace{0.05cm},$$
- $$t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot \big [0.243+0.086\big ]+ k_2 \cdot \big [1.000 + 0.059 \big ]= 0 \hspace{0.05cm}.$$
$\text{Fazit:}$ Die Ergebnisse können wie folgt verallgemeinert werden:
- Mit einem Laufzeitfilter $N$–ter Ordnung können der Hauptwert $g_d(0)$ zu Eins (normiert) sowie die ersten $N$ Nachläufer $g_{\nu}$ und die ersten $N$ Vorläufer $g_{-\nu}$ zu Null gemacht werden.
- Weitere Vor– und Nachläufer $(\nu \gt N)$ lassen sich so nicht kompensieren. Es ist sogar möglich, dass die Vor– und Nachläufer außerhalb des Kompensationsbereichs vergrößert werden oder sogar neu entstehen.
- Im Grenzübergang $N \to \infty$ (in der Praxis heißt das: ein Filter mit sehr vielen Koeffizienten) ist eine vollständige Nyquistentzerrung und damit eine impulsinterferenzfreie Übertragung möglich.
Beschreibung im Frequenzbereich
Die Tatsache, dass sich der optimale Nyquistentzerrer multiplikativ aus
- dem Matched–Filter $H_{\rm MF}(f) = H_{\rm S}^\star (f)\cdot H_{\rm K}^\star(f)$ – also angepasst an den Empfangsgrundimpuls $g_e(t)$ – und
- einem Transversalfilter $H_{\rm MF}(f) $ mit unendlich vielen Filterkoeffizienten
zusammensetzt, folgt aus dem ersten Nyquistkriterium. Durch Anwendung der Variationsrechnung erhält man den Frequenzgang des Transversalfilters – siehe [ST85][1]:
- $$H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2} \hspace{0.3cm}{\rm{mit}}\hspace{0.3cm}H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f) \hspace{0.05cm}.$$
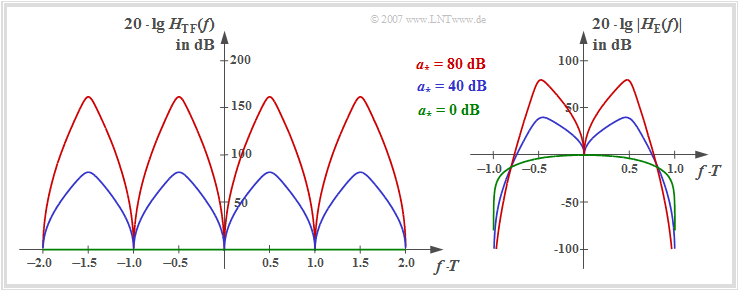
Die linke Grafik zeigt den Funktionsverlauf $20 \cdot \lg \ H_{\rm TF}(f)$ im Bereich $| f | \le 1/T$. Vorausgesetzt sind hierfür rechteckförmige NRZ–Sendeimpulse und ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_\star$.
Man erkennt aus obiger Gleichung und der linken Grafik:
- $H_{\rm TF}(f)$ ist reell, woraus sich die symmetrische Struktur des Transversalfilters ergibt: $k_{-\lambda} =k_{-\lambda} $.
- $H_{\rm TF}(f)$ ist gleichzeitig eine mit der Frequenz $1/T$ periodische Funktion.
- Die Koeffizienten ergeben sich somit aus der Fourierreihe (angewandt auf die Spektralfunktion):
- $$k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2} \hspace{0.2cm} {\rm d} f \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.$$
In der rechten Grafik ist der Frequenzgang $20 \cdot \lg \ |H_{\rm E}(f)|$ des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt:
- $$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}.$$
Zu diesen Darstellungen ist anzumerken:
- Für $a_\star = 0 \ \rm dB$ (idealer Kanal, grüne Null–Linie) kann auf das Transversalfilter $H_{\rm TF}(f)$ verzichtet werden und es gilt für NRZ–Rechteckimpulse , wie bereits im Abschnitt Optimaler Binärempfänger – Realisierung mit Matched-Filter hergeleitet: $H_{\rm E}(f) =H_{\rm S}(f) = {\rm si} (\pi f T).$
- Während der Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ bei $a_\star \ne 0 \ \rm dB$ symmetrisch zur Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$ ist, ist diese Symmetrie beim Empfangsfilter–Gesamtfrequenzgang $H_{\rm E}(f)$ nicht mehr gegeben.
- Die Maxima der Frequenzgänge $H_{\rm TF}(f)$ und $|H_{\rm E}(f)|$ hängen signifikant von der charakteristischen Kabeldämpfung $a_\star$ ab. Aus dem blauen bzw. roten Funktionsverlauf kann abgelesen werden:
- $$a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)| \ \big] \approx 40\,{\rm dB}\hspace{0.05cm},$$
- $$a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}\big[H_{\rm TF}(f)\big] \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}\big[\ |H_{\rm E}(f)|\ \big] \approx 80\,{\rm dB}\hspace{0.05cm}.$$
Approximation des optimalen Nyquistentzerrers
Betrachten wir nun den Gesamtfrequenzgang zwischen der Diracquelle und dem Entscheider.
- Dieser setzt sich multiplikativ aus den Frequenzgängen von Sender, Kanal und Empfänger zusammen.
- Entsprechend der Herleitung muss der Gesamtfrequenzgang die Nyquistbedingung erfüllen:
- $$H_{\rm Nyq}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f) = \frac{|H_{\rm SK}(f)|^2}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$
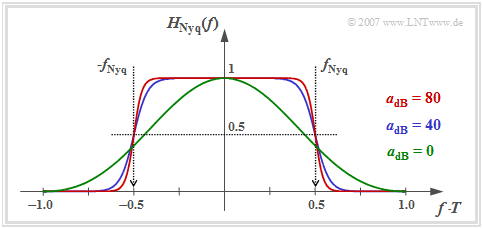
Die Grafik zeigt folgende Eigenschaften des optimalen Nyquistentzerrers (ONE):
- Ist die Kabeldämpfung hinreichend groß $(a_\star \ge 10 \ \rm dB)$, so kann man den Gesamtfrequenzgang mit guter Näherung durch einen Cosinus–Rolloff–Tiefpass beschreiben.
- Je größer $a_\star$ ist, desto kleiner ist der Rolloff–Faktor $r$ und um so steiler verläuft der Flankenabfall. Für die charakteristische Kabeldämpfung $a_\star = 40 \ \rm dB$ (blaue Kurve) ergibt sich $r \approx 0.4$, für $a_\star = 80 \ \rm dB$ (rote Kurve) $r \approx 0.18$.
- Oberhalb der Frequenz $f_{\rm Nyq} \cdot (1 + r)$ besitzt $H_{\rm Nyq}(f)$ keine Anteile. Bei idealem Kanal ⇒ $a_\star = 0 \ \rm dB$ (grüne Kurve) reicht $H_{\rm Nyq}(f)= {\rm si}^2(\pi f T)$ allerdings theoretisch bis ins Unendliche.
Das Interaktionsmodul Tiefpässe im Frequenz- und Zeitbereich verdeutlicht die Eigenschaften des Cosinus–Rolloff–Tiefpasses.
Berechnung der normierten Störleistung
Betrachten wir nun noch die (normierte) Störleistung am Entscheider. Für diese gilt:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ (2T)} =T \cdot \int_{-1/(2T)}^{+1/(2T)} |H_{\rm E}(f)|^2 \,{\rm d} f .$$
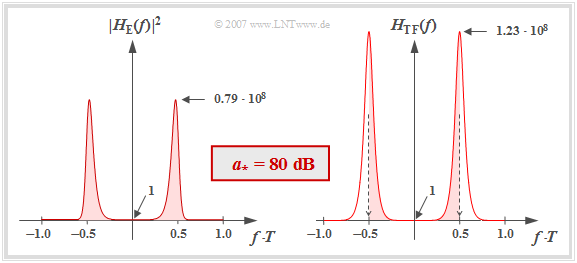
Das linke Bild zeigt $|H_{\rm E}(f)|^2$ im linearen Maßstab für die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$. Beachten Sie, dass $|H_{\rm E}(f = 0)|^2 = 1$ ist.
Da die Frequenz in dieser Darstellung auf $1/T$ normiert wurde, entspricht die normierte Störleistung genau der (rot hinterlegten) Fläche unter dieser Kurve. Die numerische Auswertung ergibt:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = 1.68 \cdot 10^7$$
- $$\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 \approx 72.25\,{\rm dB} \hspace{0.05cm}.$$
Es kann gezeigt werden, dass die normierte Störleistung allein mit dem Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ berechnet werden kann, wie in der rechten Grafik dargestellt:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f \hspace{0.3cm}(= k_0)\hspace{0.05cm}.$$
Die roten Flächen sind in beiden Bildern exakt gleich.
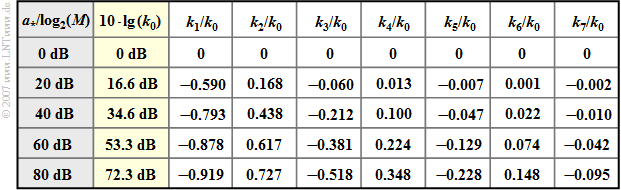
$\text{Fazit:}$ Die normierten Störleistung des optimalen Nyquistentzerrers ist gleich dem Fourierkoeffizienten $k_0$, wenn man den reellen, symmetrischen und periodischen Transversalfilter–Frequenzgang $H_{\rm TF}(f)$ als Fourierreihe darstellt.
- In der zweiten Spalte der Tabelle ist $10 \cdot \lg \ (k_0)$ in Abhängigkeit der charakteristischen Kabeldämpfung $a_\star$ eines Koaxialkabels angegeben.
- Aufgrund der gewählten Normierung gilt die Tabelle auch für redundanzfreie Mehrstufensysteme; $M$ bezeichnet hierbei die Stufenzahl.
- Die Koeffizienten $k_1$, $k_2$, $k_3$, ... des Transversalfilters weisen für $a_\star \ne 0 \ \rm dB$ alternierende Vorzeichen auf.
- Für $a_\star = 40 \ \rm dB$ sind vier Koeffizienten betragsmäßig größer als $k_0/10$, für $a_\star = 80 \ \rm dB$ sogar sieben.
Vergleich anhand des Systemwirkungsgrades
Für einen Systemvergleich eignet sich der Systemwirkungsgrad, der das erreichbare Detektions–SNR $\rho_d$ in Bezug zum maximalen SNR $\rho_{d, \ {\rm max}}$ setzt, das allerdings nur bei idealem Kanal $H_{\rm K}(f) \equiv 1$ erreichbar ist. Für den Systemwirkungsgrad gilt bei $M$–stufiger Übertragung und optimaler Nyquistentzerrung:
- $$\eta = \frac{\rho_d}{s_0^2 \cdot T / N_0}=\frac{{\rm log_2}\hspace{0.1cm}M}{(M-1)^2 \cdot k_0}.$$
Die (normierte) Störleistung $k_0$ kann aus der Tabelle auf der letzten Seite abgelesen werden. Beachten Sie die Normierung der charakteristischen Kabeldämpfung $a_\star$ in der ersten Spalte.
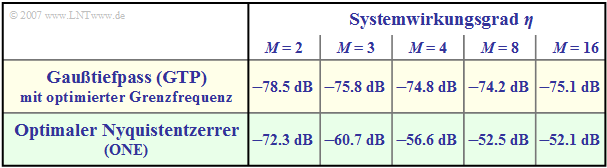
Die folgende Tabelle aus [ST85][1] ermöglicht einen Systemvergleich für die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$.
Verglichen werden:
- der gaußförmige Gesamtfrequenzgang (GTP), der auch bei Optimierung zu einem impulsinterferenzbehafteten System führt,
- der optimale Nyquistentzerrer (ONE), mit dem Impulsinterferenzen per se ausgeschlossen werden.
$\text{Fazit:}$ Die Ergebnisse dieses Systemvergleichs können wie folgt zusammengefasst werden:
- Im binären Fall $(M = 2)$ ist das impulsinterferenzfreie System (ONE) um etwa $6 \ \rm dB$ besser als das impulsinterferenzbehaftete System (GTP).
- Wendet man die optimale Nyquistentzerrung bei Mehrstufensystemen an, so ist gegenüber „GTP” ein weiterer, deutlicher Störabstandsgewinn möglich. Für $M =4$ beträgt dieser Gewinn etwa $18.2 \ \rm dB$.
- Das schmalbandige GTP–System kann allerdings deutlich verbessert werden, wenn man einen Empfänger mit Entscheidungsrückkopplung verwendet. Dieser wird im nächsten Kapitel behandelt.
Wir verweisen andieser Stelle auf das Interaktionsmodul Lineare Nyquistentzerrung.
Aufgaben zum Kapitel
Aufgabe 3.6: Transversalfilter des Optimalen Nyquistentzerrers
Aufgabe 3.6Z: Optimaler Nyquistentzerrer für Exponentialimpuls
Aufgabe 3.7: Nochmals Optimale Nyquistentzerrung
Aufgabe 3.7Z: Regeneratorfeldlänge
Quellenverzeichnis