Modulationsverfahren/Rauscheinfluss bei Winkelmodulation: Unterschied zwischen den Versionen
| Zeile 11: | Zeile 11: | ||
*der Frequenz (Bandbreite) $B_{\rm NF}$ des cosinusförmigen Quellensignals, | *der Frequenz (Bandbreite) $B_{\rm NF}$ des cosinusförmigen Quellensignals, | ||
*der Sendeleistung $P_{\rm S}$, | *der Sendeleistung $P_{\rm S}$, | ||
| − | *des | + | *des Kanalübertragungsfaktors $α_{\rm K}$, und |
*der (einseitigen) Rauschleistungsdichte $N_0$. | *der (einseitigen) Rauschleistungsdichte $N_0$. | ||
| Zeile 27: | Zeile 27: | ||
*Man approximiert das weiße Rauschen $n(t)$ mit der Bandbreite $B_{\rm HF}$ durch eine Summe von Sinusstörern im Abstand $f_{\rm St}$ (siehe zweite Skizze im nächsten Abschnitt). | *Man approximiert das weiße Rauschen $n(t)$ mit der Bandbreite $B_{\rm HF}$ durch eine Summe von Sinusstörern im Abstand $f_{\rm St}$ (siehe zweite Skizze im nächsten Abschnitt). | ||
*Man berechnet für jeden Sinusstörer das S/N–Verhältnis nach der Demodulation und addiert die einzelnen Beiträge, die nun alle im Tiefpassbereich $|f| < B_{\rm NF}$ liegen. | *Man berechnet für jeden Sinusstörer das S/N–Verhältnis nach der Demodulation und addiert die einzelnen Beiträge, die nun alle im Tiefpassbereich $|f| < B_{\rm NF}$ liegen. | ||
| − | *Das obige einfache Ergebnis erhält man nach dem Grenzübergang $f_{\rm St} → 0$. Die Summe geht dann in ein Integral über und dieses kann näherungsweise gelöst werden. | + | *Das obige einfache Ergebnis erhält man nach dem Grenzübergang $f_{\rm St} → 0$. Die Summe geht dann in ein Integral über und dieses kann näherungsweise gelöst werden. |
==Signal–zu–Rausch–Leistungsverhältnis bei FM== | ==Signal–zu–Rausch–Leistungsverhältnis bei FM== | ||
| Zeile 34: | Zeile 34: | ||
Zur Berechnung nutzt man hier die Tatsache, dass der FM–Demodulator mit einem PM–Demodulator und einem Differenzierer realisiert werden kann. | Zur Berechnung nutzt man hier die Tatsache, dass der FM–Demodulator mit einem PM–Demodulator und einem Differenzierer realisiert werden kann. | ||
| − | *Das Blockschaltbild bezieht sich allein auf die Rauschsignale ⇒ $s(t) = 0$. | + | *Das rechts angegebene Blockschaltbild bezieht sich allein auf die Rauschsignale ⇒ $s(t) = 0$. |
*Damit ist das Empfangssignal $r(t) = n(t)$, wobei für $n(t)$ additives weißes Gaußsches Rauschen mit der Mittenfrequenz $f_{\rm T}$ und der Bandbreite $B_{\rm HF}$ anzusetzen ist. | *Damit ist das Empfangssignal $r(t) = n(t)$, wobei für $n(t)$ additives weißes Gaußsches Rauschen mit der Mittenfrequenz $f_{\rm T}$ und der Bandbreite $B_{\rm HF}$ anzusetzen ist. | ||
<br clear=all> | <br clear=all> | ||
| Zeile 42: | Zeile 42: | ||
:$${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} } (f) \cdot | :$${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} } (f) \cdot | ||
|H(f)|^2 \hspace{0.05cm}.$$ | |H(f)|^2 \hspace{0.05cm}.$$ | ||
| − | *Der Differenzierer ist ein solches lineares System. Sein Frequenzgang $H(f)$ steigt linear mit $f$ an, und es gilt für die Rauschleistungsdichte am Ausgang des FM | + | *Der Differenzierer ist ein solches lineares System. Sein Frequenzgang $H(f)$ steigt linear mit $f$ an, und es gilt für die Rauschleistungsdichte am Ausgang des FM–Demodulators (siehe rechte Skizze in der unteren Grafik): |
:$${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = {\rm const. } \cdot | :$${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = {\rm const. } \cdot | ||
f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} }(f) \hspace{0.05cm}.$$ | f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} }(f) \hspace{0.05cm}.$$ | ||
| Zeile 48: | Zeile 48: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\rm Fazit\text{:}$ | $\rm Fazit\text{:}$ | ||
| − | Berücksichtigt man dieses Ergebnis, so kommt man nach längerer Rechnung zum folgenden Sinken–SNR | + | Berücksichtigt man dieses Ergebnis, so kommt man nach längerer Rechnung zum folgenden Sinken–SNR (falls die Leistungskenngröße $ξ$ hinreichend groß ist): |
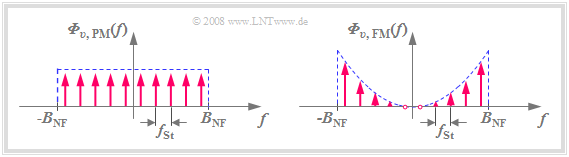
[[Datei:P_ID1114__Mod_T_3_3_S2b_neu.png |right|frame| Rauschleistungsdichtespektren bei PM (links) und FM (rechts)]] | [[Datei:P_ID1114__Mod_T_3_3_S2b_neu.png |right|frame| Rauschleistungsdichtespektren bei PM (links) und FM (rechts)]] | ||
| − | :$$\rho_{v } \approx \frac{3\eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} } = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$ | + | :$$\rho_{v } \approx \frac{3\cdot \eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} } = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$ |
Die Grafik verdeutlicht: | Die Grafik verdeutlicht: | ||
| Zeile 67: | Zeile 67: | ||
Diese qualitativ zu verstehenden Kurven sind wie folgt zu interpretieren: | Diese qualitativ zu verstehenden Kurven sind wie folgt zu interpretieren: | ||
| − | *Die ' | + | *Die Vergleichskurve liefert die '''ZSB–AM ohne Träger''' ⇒ Modulationsgrad $m → ∞$. Hier gilt $ρ_v = ξ$ und auch bei doppelt–logarithmischer Darstellung ergibt sich eine $45^\circ$–Gerade durch den Ursprung. |
| − | *Die ''FM–Kurve'' mit $η = 3$ liegt um $10 · \lg \ 13.5 ≈ 11.3 \ \rm dB$ über der AM–Kurve. Anschaulich kann man das bessere Rauschverhalten der Frequenzmodulation dadurch erklären, dass ein additiver Rauschanteil die Lage der Nulldurchgänge weniger beeinflusst als er die Amplitudenwerte verändert. | + | *Die '''FM–Kurve''' mit $η = 3$ liegt um $10 · \lg \ 13.5 ≈ 11.3 \ \rm dB$ über der AM–Kurve. Anschaulich kann man das bessere Rauschverhalten der Frequenzmodulation dadurch erklären, dass ein additiver Rauschanteil die Lage der Nulldurchgänge weniger beeinflusst als er die Amplitudenwerte verändert. |
| − | *Ist das wirksame Rauschen sehr groß und damit die Leistungskenngröße klein $(10 · \lg \ ξ ≤ 15 \ \rm dB)$, so ist Winkelmodulation nicht zu empfehlen. Aufgrund des Rauschens können dann Nulldurchgänge völlig verschwinden und so deren Detektion unmöglich machen. Man spricht vom | + | *Ist das wirksame Rauschen sehr groß und damit die Leistungskenngröße klein $(10 · \lg \ ξ ≤ 15 \ \rm dB)$, so ist Winkelmodulation nicht zu empfehlen. Aufgrund des Rauschens können dann Nulldurchgänge völlig verschwinden und so deren Detektion unmöglich machen. Man spricht vom „FM–Knick”. |
| − | *Hinsichtlich Rauschen ist bei jeder Art von Winkelmodulation ein ''möglichst großer Modulationsindex'' anzustreben. So liegt die Kurve für $η = 10$ um etwa $10.4 \ \rm dB$ über der Kurve für $η = 3$. Zu berücksichtigen ist allerdings, dass ein größeres $η$ auch eine größere Bandbreite erfordert oder – bei gegebener Kanalbandbreite – stärkere nichtlineare Verzerrungen hervorruft. | + | *Hinsichtlich Rauschen ist bei jeder Art von Winkelmodulation ein ''möglichst großer Modulationsindex'' anzustreben. So liegt die Kurve für $η = 10$ um etwa $10.4 \ \rm dB$ über der Kurve für $η = 3$. Zu berücksichtigen ist allerdings, dass ein größeres $η$ auch eine größere Bandbreite erfordert oder – bei gegebener Kanalbandbreite – stärkere nichtlineare Verzerrungen hervorruft. |
| − | *Bei gleichem Modulationsindex ist die Phasenmodulation stets um $10 \cdot \lg \ 3 ≈ 4.8 \ \rm dB$ schlechter als die Frequenzmodulation. Dies ist einer der Gründe, warum die analoge Phasenmodulation in der Praxis nur wenig Bedeutung hat. Dagegen wird bei digitaler Modulation die Variante ''Phase Shift Keying'' (PSK) aufgrund anderer Vorteile häufiger eingesetzt als ''Frequency Shift Keying'' (FSK). | + | *Bei gleichem Modulationsindex ist die Phasenmodulation ('''PM''') stets um $10 \cdot \lg \ 3 ≈ 4.8 \ \rm dB$ schlechter als die Frequenzmodulation (FM). Dies ist einer der Gründe, warum die analoge Phasenmodulation in der Praxis nur wenig Bedeutung hat. Dagegen wird bei digitaler Modulation die Variante ''Phase Shift Keying'' ('''PSK''') aufgrund anderer Vorteile häufiger eingesetzt als ''Frequency Shift Keying'' ('''FSK'''). |
| − | *Alle angegebenen Kurven gelten quantitativ nur für eine harmonische Schwingung (also für nur eine einzige Frequenz). Bei einem Frequenzgemisch – das in der Praxis stets vorliegt – gelten die Kurven aber zumindest qualitativ. | + | *Alle angegebenen Kurven gelten quantitativ nur für eine harmonische Schwingung (also für nur eine einzige Frequenz). Bei einem Frequenzgemisch – das in der Praxis stets vorliegt – gelten die Kurven aber zumindest qualitativ. |
==Preemphase und Deemphase== | ==Preemphase und Deemphase== | ||
<br> | <br> | ||
| − | Ein wichtiges Ergebnis der letzten Abschnitte war, dass das Sinken–SNR bei FM entsprechend $\rho_{v } \approx 1.5 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}$ in guter Näherung quadratisch vom Modulationsindex abhängt. Da aber bei Frequenzmodulation der Modulationsindex $η$ umgekehrt proportional zur Nachrichtenfrequenz $f_{\rm N}$ ist, hängt auch das Sinken–SNR von $f_{\rm N}$ ab. | + | Ein wichtiges Ergebnis der letzten Abschnitte war, dass das Sinken–SNR bei FM entsprechend $\rho_{v } \approx 1.5 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}$ in guter Näherung quadratisch vom Modulationsindex abhängt. Da aber bei Frequenzmodulation der Modulationsindex $η$ umgekehrt proportional zur Nachrichtenfrequenz $f_{\rm N}$ ist, hängt auch das Sinken–SNR von $f_{\rm N}$ ab. |
Daraus ergeben sich folgende Konsequenzen: | Daraus ergeben sich folgende Konsequenzen: | ||
*Besteht das Nachrichtensignal aus mehreren Frequenzen, so weisen die höheren Frequenzen nach einer FM–Modulation einen kleineren Modulationsindex $η$ auf als die niedrigeren Frequenzen. | *Besteht das Nachrichtensignal aus mehreren Frequenzen, so weisen die höheren Frequenzen nach einer FM–Modulation einen kleineren Modulationsindex $η$ auf als die niedrigeren Frequenzen. | ||
| − | *Das bedeutet auch: Die höheren Frequenzanteile $($mit kleinerem $η)$ sind dementsprechend stärker verrauscht als niedrigere Frequenzen, wenn nicht besondere Maßnahmen getroffen werden. | + | *Das bedeutet auch: Die höheren Frequenzanteile $($mit kleinerem $η)$ sind dementsprechend stärker verrauscht als niedrigere Frequenzen, wenn nicht besondere Maßnahmen getroffen werden. |
[[Datei:Mod_T_3_3_S4_version2.png|right|frame| Preemphase und Deemphase]] | [[Datei:Mod_T_3_3_S4_version2.png|right|frame| Preemphase und Deemphase]] | ||
| − | Eine solche Maßnahme ist beispielsweise eine ''Preemphase''. Dabei werden höhere Frequenzen durch ein Hochpass–Filternetzwerk $H_{\rm PE}(f)$ angehoben und für diese der Modulationsindex $η$ erhöht. | + | Eine solche Maßnahme ist beispielsweise eine '''Preemphase'''. Dabei werden höhere Frequenzen durch ein Hochpass–Filternetzwerk $H_{\rm PE}(f)$ angehoben und für diese der Modulationsindex $η$ erhöht. |
| − | Die sendeseitige Preemphase muss beim Empfänger durch ein Netzwerk $H_{\rm DE}(f) = 1/H_{\rm PE}(f)$ rückgängig gemacht werden. Dieses Absenken der höheren Frequenzen nennt man ''Deemphase. | + | Die sendeseitige Preemphase muss beim Empfänger durch ein Netzwerk $H_{\rm DE}(f) = 1/H_{\rm PE}(f)$ rückgängig gemacht werden. Dieses Absenken der höheren Frequenzen nennt man '''Deemphase'''. |
Die Grafik zeigt ein mögliches Beispiel für die Filterfunktionen von | Die Grafik zeigt ein mögliches Beispiel für die Filterfunktionen von | ||
Version vom 28. März 2020, 17:27 Uhr
Inhaltsverzeichnis
Signal–zu–Rausch–Leistungsverhältnis bei PM
Zur Untersuchung des Rauschverhaltens gehen wir wieder vom so genannten AWGN–Kanal aus und berechnen das Sinken–SNR $ρ_v$ in Abhängigkeit
- der Frequenz (Bandbreite) $B_{\rm NF}$ des cosinusförmigen Quellensignals,
- der Sendeleistung $P_{\rm S}$,
- des Kanalübertragungsfaktors $α_{\rm K}$, und
- der (einseitigen) Rauschleistungsdichte $N_0$.
Die prinzipielle Vorgehensweise wird im Abschnitt Untersuchungen beim AWGN-Kanal ausführlich beschrieben:
Ist die Leistungskenngröße
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
hinreichend groß, so erhält man bei Phasenmodulation mit dem Modulationsindex $η$ folgende Näherung:
- $$\rho_{v } \approx {\eta^2}/{2} \cdot\xi \hspace{0.05cm}.$$
Das bedeutet, dass bei Phasenmodulation das Sinken–SNR mit wachsendem $η$ quadratisch zunimmt.
Die exakte Berechnung von $ρ_v$ ist nicht ganz einfach und auch langwierig. Hier soll nur der Rechenweg kurz geschildert werden:
- Man approximiert das weiße Rauschen $n(t)$ mit der Bandbreite $B_{\rm HF}$ durch eine Summe von Sinusstörern im Abstand $f_{\rm St}$ (siehe zweite Skizze im nächsten Abschnitt).
- Man berechnet für jeden Sinusstörer das S/N–Verhältnis nach der Demodulation und addiert die einzelnen Beiträge, die nun alle im Tiefpassbereich $|f| < B_{\rm NF}$ liegen.
- Das obige einfache Ergebnis erhält man nach dem Grenzübergang $f_{\rm St} → 0$. Die Summe geht dann in ein Integral über und dieses kann näherungsweise gelöst werden.
Signal–zu–Rausch–Leistungsverhältnis bei FM
Zur Berechnung nutzt man hier die Tatsache, dass der FM–Demodulator mit einem PM–Demodulator und einem Differenzierer realisiert werden kann.
- Das rechts angegebene Blockschaltbild bezieht sich allein auf die Rauschsignale ⇒ $s(t) = 0$.
- Damit ist das Empfangssignal $r(t) = n(t)$, wobei für $n(t)$ additives weißes Gaußsches Rauschen mit der Mittenfrequenz $f_{\rm T}$ und der Bandbreite $B_{\rm HF}$ anzusetzen ist.
Bei der Berechnung der Rauschleistungsdichte nach dem FM–Demodulator ist zu berücksichtigen:
- Die Rauschleistungsdichte ${\it Φ}_{v,\hspace{0.05cm}{\rm PM}}(f)$ nach dem PM–Demodulator liegt im Tiefpassbereich, besitzt die (einseitige) Bandbreite $B_{\rm NF}$ und ist ebenfalls „weiß”
(siehe linke Skizze in der unteren Grafik). - Die Leistungsdichte am Ausgang eines linearen Systems mit Frequenzgang $H(f)$ lautet allgemein, wenn am Eingang die Rauschleistungsdichte ${\it Φ}_{v,\hspace{0.05cm}{\rm PM}}(f)$ anliegt:
- $${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} } (f) \cdot |H(f)|^2 \hspace{0.05cm}.$$
- Der Differenzierer ist ein solches lineares System. Sein Frequenzgang $H(f)$ steigt linear mit $f$ an, und es gilt für die Rauschleistungsdichte am Ausgang des FM–Demodulators (siehe rechte Skizze in der unteren Grafik):
- $${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = {\rm const. } \cdot f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} }(f) \hspace{0.05cm}.$$
$\rm Fazit\text{:}$ Berücksichtigt man dieses Ergebnis, so kommt man nach längerer Rechnung zum folgenden Sinken–SNR (falls die Leistungskenngröße $ξ$ hinreichend groß ist):
- $$\rho_{v } \approx \frac{3\cdot \eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} } = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$
Die Grafik verdeutlicht:
- Die Rauschleistungsdichte ${\it Φ}_{v,\hspace{0.05cm}{\rm FM} }(f)$ ist im Gegensatz zu ${\it Φ}_{v,\hspace{0.05cm}{\rm PM} }(f)$ nicht weiß.
- Vielmehr steigt ${\it Φ}_{v,\hspace{0.05cm}{\rm FM} }(f)$ zu den Grenzen $(\pm B_{\rm NF} )$ hin quadratisch an.
- Bei $f = 0$ besitzt ${\it Φ}_{v,\hspace{0.05cm}{\rm FM} }(f)$ keine Rauschanteile.
Systemvergleich von AM, PM und FM hinsichtlich Rauschen
Wie schon im Abschnitt Untersuchungen beim AWGN-Kanal ausführlich erläutert und im Abschnitt Sinken-SNR und Leistungskenngröße auf die Amplitudenmodulation angewendet, betrachten wir wieder die doppelt-logarithmische Darstellung des Sinken–SNR $ρ_v$ über der Kenngröße
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}.$$
Diese qualitativ zu verstehenden Kurven sind wie folgt zu interpretieren:
- Die Vergleichskurve liefert die ZSB–AM ohne Träger ⇒ Modulationsgrad $m → ∞$. Hier gilt $ρ_v = ξ$ und auch bei doppelt–logarithmischer Darstellung ergibt sich eine $45^\circ$–Gerade durch den Ursprung.
- Die FM–Kurve mit $η = 3$ liegt um $10 · \lg \ 13.5 ≈ 11.3 \ \rm dB$ über der AM–Kurve. Anschaulich kann man das bessere Rauschverhalten der Frequenzmodulation dadurch erklären, dass ein additiver Rauschanteil die Lage der Nulldurchgänge weniger beeinflusst als er die Amplitudenwerte verändert.
- Ist das wirksame Rauschen sehr groß und damit die Leistungskenngröße klein $(10 · \lg \ ξ ≤ 15 \ \rm dB)$, so ist Winkelmodulation nicht zu empfehlen. Aufgrund des Rauschens können dann Nulldurchgänge völlig verschwinden und so deren Detektion unmöglich machen. Man spricht vom „FM–Knick”.
- Hinsichtlich Rauschen ist bei jeder Art von Winkelmodulation ein möglichst großer Modulationsindex anzustreben. So liegt die Kurve für $η = 10$ um etwa $10.4 \ \rm dB$ über der Kurve für $η = 3$. Zu berücksichtigen ist allerdings, dass ein größeres $η$ auch eine größere Bandbreite erfordert oder – bei gegebener Kanalbandbreite – stärkere nichtlineare Verzerrungen hervorruft.
- Bei gleichem Modulationsindex ist die Phasenmodulation (PM) stets um $10 \cdot \lg \ 3 ≈ 4.8 \ \rm dB$ schlechter als die Frequenzmodulation (FM). Dies ist einer der Gründe, warum die analoge Phasenmodulation in der Praxis nur wenig Bedeutung hat. Dagegen wird bei digitaler Modulation die Variante Phase Shift Keying (PSK) aufgrund anderer Vorteile häufiger eingesetzt als Frequency Shift Keying (FSK).
- Alle angegebenen Kurven gelten quantitativ nur für eine harmonische Schwingung (also für nur eine einzige Frequenz). Bei einem Frequenzgemisch – das in der Praxis stets vorliegt – gelten die Kurven aber zumindest qualitativ.
Preemphase und Deemphase
Ein wichtiges Ergebnis der letzten Abschnitte war, dass das Sinken–SNR bei FM entsprechend $\rho_{v } \approx 1.5 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}$ in guter Näherung quadratisch vom Modulationsindex abhängt. Da aber bei Frequenzmodulation der Modulationsindex $η$ umgekehrt proportional zur Nachrichtenfrequenz $f_{\rm N}$ ist, hängt auch das Sinken–SNR von $f_{\rm N}$ ab.
Daraus ergeben sich folgende Konsequenzen:
- Besteht das Nachrichtensignal aus mehreren Frequenzen, so weisen die höheren Frequenzen nach einer FM–Modulation einen kleineren Modulationsindex $η$ auf als die niedrigeren Frequenzen.
- Das bedeutet auch: Die höheren Frequenzanteile $($mit kleinerem $η)$ sind dementsprechend stärker verrauscht als niedrigere Frequenzen, wenn nicht besondere Maßnahmen getroffen werden.
Eine solche Maßnahme ist beispielsweise eine Preemphase. Dabei werden höhere Frequenzen durch ein Hochpass–Filternetzwerk $H_{\rm PE}(f)$ angehoben und für diese der Modulationsindex $η$ erhöht.
Die sendeseitige Preemphase muss beim Empfänger durch ein Netzwerk $H_{\rm DE}(f) = 1/H_{\rm PE}(f)$ rückgängig gemacht werden. Dieses Absenken der höheren Frequenzen nennt man Deemphase.
Die Grafik zeigt ein mögliches Beispiel für die Filterfunktionen von
- Preemphase (blau) ⇒ $|H_{{\rm PE} } (f)| = \sqrt{1 + \left({f}/{f_{\rm G}}\right)^2}\hspace{0.05cm},$
- Deemphase (rot) ⇒ $|H_{{\rm DE} } (f)| = |H_{{\rm PE} } (f)|^{-1} \hspace{0.05cm}.$
Aufgaben zum Kapitel
Aufgabe 3.10: Berechnung der Rauschleistungen
Aufgabe 3.10Z: Amplituden- und Winkelmodulation im Vergleich
Aufgabe 3.11: Preemphase und Deemphase