Pulscodemodulation

Inhaltsverzeichnis

1 # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
2 Prinzip und Blockschaltbild
3 Abtastung und Signalrekonstruktion
4 Natürliche und diskrete Abtastung
5 Frequenzbereichsbetrachtung der natürlichen Abtastung
6 Frequenzbereichsbetrachtung der diskreten Abtastung
7 Quantisierung und Quantisierungsrauschen
8 PCM–Codierung und –Decodierung
9 Signal–zu–Rausch–Leistungsverhältnis
10 Einfluss von Übertragungsfehlern
11 Abschätzung der SNR-Degradation durch Übertragungsfehler
12 Nichtlineare Quantisierung
13 Kompression und Expandierung
14 Aufgaben zum Kapitel

# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #

Das vierte Kapitel behandelt die digitalen Modulationsverfahren »Amplitude Shift Keying« $\rm (ASK)$, »Phase Shift Keying« $\rm (PSK)$ und »Frequency Shift Keying« $\rm (FSK)$ sowie einige davon abgeleitete Modifikationen. Die meisten der in den beiden letzten Kapiteln genannten Eigenschaften der analogen Modulationsverfahren gelten weiterhin. Unterschiede ergeben sich aus der nun erforderlichen Entscheiderkomponente des Empfängers.

Wir beschränken uns hier im wesentlichen auf die systemtheoretischen und übertragungstechnischen Aspekte. Die Fehlerwahrscheinlichkeit wird nur für ideale Bedingungen angegeben. Die ausführlichen Herleitungen und die Berücksichtigung nichtidealer Randbedingungen finden Sie im Buch „Digitalsignalübertragung”.

Im Einzelnen werden behandelt:

die »Pulscodemodulation« $\rm (PCM)$ und deren Komponenten »Abtastung« – »Quantisierung« – »Codierung«,
die »linearen Modulationsverfahren« $\rm ASK$, $\rm BPSK$, $\rm DPSK$ sowie zugehörige Demodulatoren,
die »Quadraturamplitudenmodulation« $\rm (QAM)$ sowie kompliziertere Signalraumzuordnungen,
die »Frequency Shift Keying« $\rm (FSK)$ als Beispiel einer nichtlinearen digitalen Modulation,
die »FSK mit kontinuierlicher Phasenanpassung« $\rm (CPM)$, insbesondere das $\rm (G)MSK$–Verfahren.

Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Digitale Modulationsverfahren” des Praktikums „Simulation Digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 12: Seite 271-294.

Prinzip und Blockschaltbild

Nahezu alle heute eingesetzten Modulationsverfahren arbeiten digital. Deren Vorteile wurden schon im ersten Kapitel dieses Buches ausführlich dargelegt. Das erste Konzept zur digitalen Signalübertragung wurde bereits 1938 von Alec Reeves entwickelt und wird seit den 1960er Jahren unter dem Namen "Pulscodemodulation" $\rm (PCM)$ auch in der Praxis eingesetzt.

Blockschaltbild der Pulscodemodulation

Auch wenn sich viele der in den letzten Jahren konzipierten digitalen Modulationsverfahren von der PCM im Detail unterscheiden, so eignet sich diese doch sehr gut, um das Prinzip all dieser Verfahren zu erklären.

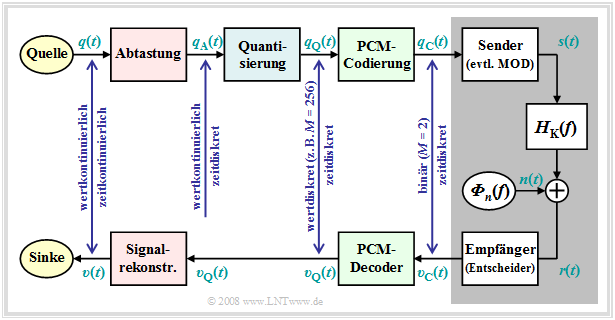
Aufgabe des PCM–Systems ist es,

das analoge Quellensignal $q(t)$ in das Binärsignal $q_{\rm C}(t)$ umzusetzen – diesen Vorgang bezeichnet man auch als A/D–Wandlung,
dieses Signal über den Kanal zu übertragen, wobei das empfängerseitige Signal $v_{\rm C}(t)$ wegen des Entscheiders ebenfalls binär ist,
schließlich aus dem Binärsignal $v_{\rm C}(t)$ das analoge, sowohl wert– als auch zeitkontinuierliche Sinkensignal $v(t)$ zu rekonstruieren ⇒ D/A–Wandlung.

Weiterhin ist zum obigen PCM–Blockschaltbild anzumerken:

Der PCM–Sender ("A/D–Wandler") setzt sich aus den drei Funktionsblöcken "Abtastung" – "Quantisierung" – "PCM–Codierung" zusammen, die in den nächsten Abschnitten noch im Detail beschrieben werden.

Der grau hinterlegte Block zeigt das digitale Übertragungssystem mit digitalem Sender (inkl. Modulator), digitalem Empfänger (inkl. Entscheider), sowie dem analogen Übertragungskanal, gekennzeichnet durch den Kanalfrequenzgang $H_{\rm K}(f)$ und die Rauschleistungsdichte ${\it Φ}_n(f)$.

Dieser Block wird in den ersten drei Kapiteln des Buches Digitalsignalübertragung eingehend behandelt. Im Kapitel 5 des gleichen Buches finden Sie auch digitale Kanalmodelle, die das Übertragungsverhalten anhand der Binärsignale $q_{\rm C}(t)$ und $v_{\rm C}(t)$ phänomenologisch beschreiben.

Weiter erkennt man aus dem obigen Blockschaltbild, dass es für die Quantisierung empfängerseitig keine Entsprechung gibt. Deshalb wird sich auch bei fehlerfreier Übertragung, also für $v_{\rm C}(t) = q_{\rm C}(t)$, das analoge Sinkensignal $v(t)$ vom Quellensignal $q(t)$ unterscheiden.

Als Maß für die Qualität des (digitalen) Übertragungssystems verwenden wir das Signal-zu-Stör-Leistungsverhältnis ⇒ kurz: Sinken–SNR als der Quotient der Leistungen von Nutzsignal $q(t)$ und Fehlersignal $ε(t) = v(t) - q(t)$:

$$\rho_{v} = \frac{P_q}{P_\varepsilon}\hspace{0.3cm} {\rm mit}\hspace{0.3cm}P_q = \overline{[q(t)]^2}, \hspace{0.2cm}P_\varepsilon = \overline{[v(t) - q(t)]^2}\hspace{0.05cm}.$$

Hierbei ist eine ideale Amplitudenanpassung vorausgesetzt, so dass im Idealfall (das heißt: Abtastung gemäß dem Abtasttheorem, bestmögliche Signalrekonstruktion, unendlich feine Quantisierung) das Sinkensignal $v(t)$ mit dem Quellensignal $q(t)$ exakt übereinstimmen würde.

⇒ Wir möchten Sie bereits hier auf das dreiteilige Lernvideo "Pulscodemodulation" hinweisen, das alle Aspekte der PCM beinhaltet.
Das PCM– Prinzip wird im ersten Teil des Videos erläutert.

Abtastung und Signalrekonstruktion

Die Abtastung – also die Zeitdiskretisierung des Analogsignals $q(t)$ – wurde im Kapitel Zeitdiskrete Signaldarstellung des Buches „Signaldarstellung” ausführlich behandelt. Hier folgt eine Kurzzusammenfassung dieses Abschnitts.

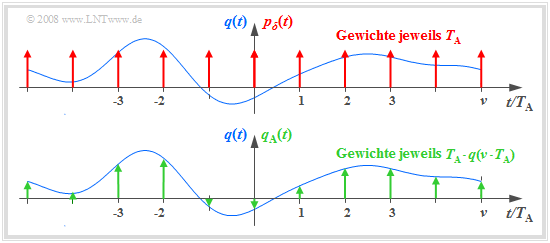
Zeitbereichsdarstellung der Abtastung

Die Grafik verdeutlicht die Abtastung im Zeitbereich:

Das (blaue) Signal $q(t)$ ist zeitkontinuierlich, das im Abstand $T_{\rm A}$ abgetastete (grüne) Signal $q_{\rm A}(t)$ zeitdiskret.
Die Abtastung lässt sich durch die Multiplikation des Analogsignals $q(t)$ mit dem Diracpuls im Zeitbereich ⇒ $p_δ(t)$ darstellen:

$$q_{\rm A}(t) = q(t) \cdot p_{\delta}(t)\hspace{0.3cm} {\rm mit}\hspace{0.3cm}p_{\delta}(t)= \sum_{\nu = -\infty}^{\infty}T_{\rm A}\cdot \delta(t - \nu \cdot T_{\rm A}) \hspace{0.05cm}.$$

Das Gewicht der Diracfunktion bei $t = ν · T_{\rm A}$ ist gleich $T_{\rm A} · q(ν · T_{\rm A})$. Da die Diracfunktion $δ(t)$ die Einheit $\rm 1/s$ aufweist, hat somit $q_{\rm A}(t)$ die gleiche Einheit wie $q(t)$, zum Beispiel „V”.

Die Fouriertransformierte des Diracpulses $p_δ(t)$ ist ebenfalls ein Diracpuls (aber nun im Frequenzbereich) ⇒ $P_δ(f)$, wobei der Abstand der einzelnen Diraclinien $f_{\rm A} = 1/T_{\rm A}$ beträgt. Alle Impulsgewichte von $P_δ(f)$ sind $1$:

$$p_{\delta}(t)= \sum_{\nu = -\infty}^{+\infty}T_{\rm A}\cdot \delta(t - \nu \cdot T_{\rm A}) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f)= \sum_{\mu = -\infty}^{+\infty} \delta(f - \mu \cdot f_{\rm A}) \hspace{0.05cm}.$$

Das Spektrum $Q_{\rm A}(f)$ des abgetasteten Signals ergibt sich aus dem Faltungssatz, wobei $Q(f)$ das kontinuierliche Spektrum des Analogsignals $q(t)$ bezeichnet:

$$Q_{\rm A}(f) = Q(f) \star P_{\delta}(f)= \sum_{\mu = -\infty}^{+\infty} Q(f - \mu \cdot f_{\rm A}) \hspace{0.05cm}.$$

⇒ Wir weisen Sie hier auf den zweiten Teil des Lernvideos "Pulscodemodulation" hin, das die Abtastung und die Signalrekonstruktion systemtheoretisch erklärt.

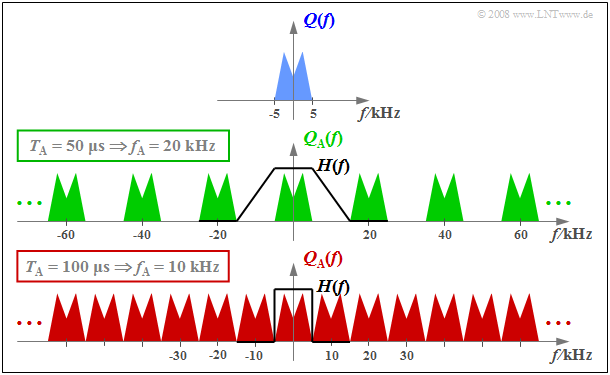
$\text{Beispiel 1:}$ Die obere Grafik zeigt schematisch das Spektrum $Q(f)$ eines analogen Quellensignals $q(t)$ mit Frequenzen bis $f_{\rm N, \ max} = 5 \ \rm kHz$.

Periodische Fortsetzung des Spektrums durch Abtastung

Tastet man $q(t)$ mit der Abtastrate $f_{\rm A} = 20 \ \rm kHz$ $($also im jeweiligen Abstand $T_{\rm A} = 50 \ \rm µ s)$ ab, so erhält man das grün skizzierte periodische Spektrum $Q_{\rm A}(f)$.

Da die Diracfunktionen unendlich schmal sind, beinhaltet $q_{\rm A}(t)$ auch beliebig hochfrequente Anteile und dementsprechend ist $Q_{\rm A}(f)$ bis ins Unendliche ausgedehnt (mittlere Grafik).

Darunter (rot) gezeichnet ist das Spektrum $Q_{\rm A}(f)$ für die Abtastparameter $T_{\rm A} = 100 \ \rm µ s$ ⇒ $f_{\rm A} = 10 \ \rm kHz$.

$\text{Fazit:}$ Aus diesem Beispiel lassen sich folgende wichtige Erkenntnisse bezüglich der Abtastung gewinnen:

Beinhaltet $Q(f)$ Frequenzanteile bis $f_\text{N, max}$, so muss nach dem Abtasttheorem die Abtastrate $f_{\rm A} ≥ 2 · f_\text{N, max}$ gewählt werden. Bei kleinerer Abtastrate $f_{\rm A}$ $($also größerem Abstand $T_{\rm A})$ kommt es zu Überlappungen der periodifizierten Spektren, also zu irreversiblen Verzerrungen.

Gilt exakt $f_{\rm A} = 2 · f_\text{N, max}$ wie in der unteren Grafik von $\text{Beispiel 1}$, so kann $Q(f)$ aus $Q_{\rm A}(f)$ – bzw. im PCM–System $V(f)$ aus $V_{\rm Q}(f)$ – durch einen idealen rechteckförmigen Tiefpass $H(f)$ mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2$ vollständig rekonstruiert werden.

Erfolgt dagegen die Abtastung mit $f_{\rm A} > 2 · f_\text{N, max}$ wie in der mittleren Grafik des Beispiels, so kann empfängerseitig zur Signalrekonstruktion auch ein Tiefpass $H(f)$ mit kleinerer Flankensteilheit verwendet werden, solange die folgende Bedingung erfüllt ist:

$$H(f) = \left\{ \begin{array}{l} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r} } \\{\rm{f\ddot{u}r} } \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left \vert \hspace{0.005cm} f\hspace{0.05cm} \right \vert \le f_{\rm N, \hspace{0.05cm}max},} \\ {\hspace{0.04cm}\left \vert\hspace{0.005cm} f \hspace{0.05cm} \right \vert \ge f_{\rm A}- f_{\rm N, \hspace{0.05cm}max}.} \\ \end{array}$$

Natürliche und diskrete Abtastung

Die Multiplikation mit dem Diracpuls liefert nur eine idealisierte Beschreibung der Abtastung, da eine Diracfunktion $($Dauer $T_{\rm R} → 0$, Höhe $1/T_{\rm R} → ∞)$ nicht realisierbar ist. In der Praxis muss der Diracpuls $p_δ(t)$ zum Beispiel durch einen "Rechteckpuls"

Rechteckpuls (oben) sowie natürliche und diskrete Abtastung

$$p_{\rm R}(t)= \sum_{\nu = -\infty}^{+\infty}g_{\rm R}(t - \nu \cdot T_{\rm A}),$$

$$g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c}{\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \\{\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \\ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm}. \\ \end{array}$$

ersetzt werden, wobei die Rechteckimpulsdauer $T_{\rm R}$ deutlich kleiner als der Abtastabstand $T_{\rm A}$ sein sollte.

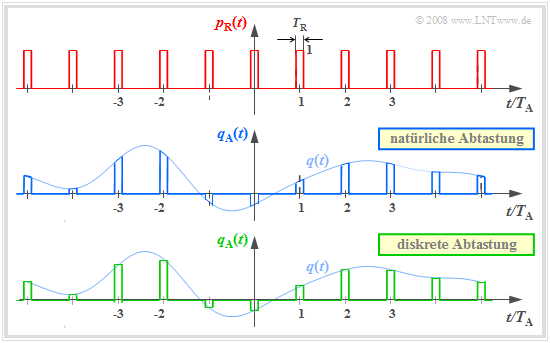
Die Grafik zeigt oben den Rechteckpuls $p_{\rm R}(t)$. Darunter sind zwei verschiedene Abtastverfahren mit diesem Rechteckpuls dargestellt:

Bei der natürlichen Abtastung ergibt sich das abgetastete Signal $q_{\rm A}(t)$ durch Multiplikation von $q(t)$ mit $p_{\rm R}(t)$. In den Bereichen $p_{\rm R}(t) = 1$ hat somit $q_{\rm A}(t)$ den gleichen Verlauf wie $q(t)$.

Bei der diskreten Abtastung wird das Signal $q(t)$ – zumindest gedanklich – erst mit dem Diracpuls $p_δ(t)$ multipliziert. Dann wird jeder Diracimpuls $T_{\rm A} · δ(t - ν · T_{\rm A})$ durch einen Rechteckimpuls $g_{\rm R}(t - ν · T_{\rm A})$ ersetzt.

Hier und bei der nachfolgenden Frequenzbereichsbetrachtung ist zur Vereinfachung eine akausale Beschreibungsform gewählt. Für eine (kausale) Realisierung müsste $g_{\rm R}(t) = 1$ im Bereich von $0$ bis $T_{\rm R}$ gelten, und nicht wie hier für $ \ -T_{\rm R}/2 < t < T_{\rm R}/2.$

Frequenzbereichsbetrachtung der natürlichen Abtastung

$\text{Definition:}$ Die natürliche Abtastung lässt sich mit dem Faltungssatz im Spektralbereich wie folgt darstellen:

$$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A} } \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \cdot \frac{1}{T_{\rm A} } \cdot G_{\rm R}(f) \right ] \star Q(f) = P_{\rm R}(f) \star Q(f)\hspace{0.05cm}.$$

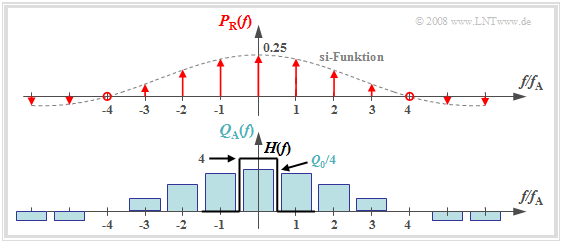
Die Grafik zeigt das Ergebnis für

ein (unrealistisches) rechteckförmiges Spektrum $Q(f) = Q_0$, das auf den Bereich $|f| ≤ 4 \ \rm kHz$ begrenzt ist,
die Abtastrate $f_{\rm A} = 10 \ \rm kHz$ ⇒ $T_{\rm A} = 100 \ \rm µ s$, sowie
die Rechteckimpulsdauer $T_{\rm R} = 25 \ \rm µ s$ ⇒ $T_{\rm R}/T_{\rm A} = 0.25$.

Spektrum bei natürlicher Abtastung mit einem Rechteckpuls

Man erkennt aus dieser Darstellung:

Das Spektrum $P_{\rm R}(f)$ bei natürlicher Abtastung ist im Gegensatz zu $P_δ(f)$ kein Diracpuls $($alle Gewichte gleich $1)$, sondern die Gewichte sind hier mit $G_{\rm R}(f)/T_{\rm A} = T_{\rm R}/T_{\rm A} · {\rm si}(πfT_{\rm R})$ bewertet.
Wegen der ersten Nullstelle der $\rm si$–Funktion verschwinden hier die Diraclinien bei $±4f_{\rm A}$.
Das Spektrum $Q_{\rm A}(f)$ ergibt sich aus der Faltung mit $Q(f)$. Das Rechteck um $f = 0$ hat die Höhe $T_{\rm R}/T_{\rm A} · Q_0$, die Anteile um $\mu · f_{\rm A} \ (\mu ≠ 0)$ sind weniger hoch.
Verwendet man zur Signalrekonstruktion einen idealen (rechteckförmigen) Tiefpass

$$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} = 4 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}, \\ \end{array}$$

so gilt für das Ausgangsspektrum $V(f) = Q(f)$. Dementsprechend gilt auch $v(t) = q(t)$.

$\text{Fazit:}$

Bei natürlicher Abtastung genügt zur Signalrekonstruktion wie bei idealer Abtastung (mit Diracpuls) ein Rechteck–Tiefpass.
Allerdings muss zur Amplitudenanpassung im Durchlassbereich eine Verstärkung um den Faktor $T_{\rm A}/T_{\rm R}$ berücksichtigt werden.

Frequenzbereichsbetrachtung der diskreten Abtastung

$\text{Definition:}$ Bei der diskreten Abtastung erfolgt – zumindest gedanklich – zunächst die Multiplikation des Diracpulses $p_δ(t)$ mit dem Quellensignal $q(t)$ und erst danach die Faltung mit dem Rechteckimpuls $g_{\rm R}(t)$:

$$q_{\rm A}(t) = \big [ {1}/{T_{\rm A} } \cdot p_{\rm \delta}(t) \cdot q(t)\big ]\star g_{\rm R}(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \big [ P_{\rm \delta}(f) \star Q(f) \big ] \cdot G_{\rm R}(f)/{T_{\rm A} } \hspace{0.05cm}.$$

Es ist unerheblich, aber durchaus zweckmäßig, dass hier der Faktor $1/T_{\rm A}$ zur Bewertungsfunktion $G_{\rm R}(f)$ hinzugefügt wurde.
Damit gilt wieder $G_{\rm R}(f)/T_{\rm A} = T_{\rm R}/T_{\rm A} · {\rm si}(πfT_{\rm R}).$

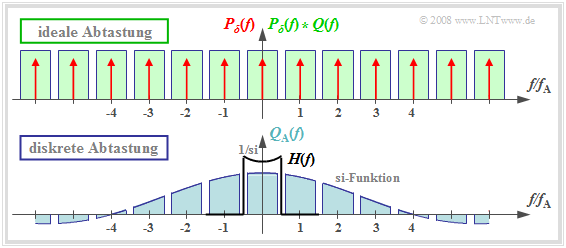
Spektrum bei diskreter Abtastung mit einem Rechteckpuls

Die obere Grafik zeigt (grün hinterlegt) die Spektralfunktion $P_δ(f) \star Q(f)$ nach idealer Abtastung.
Bei diskreter Abtastung mit einem Rechteckpuls ergibt sich dagegen das Spektrum $Q_{\rm A}(f)$ entsprechend dem unteren Diagramm.

Man erkennt:

Jedes der unendlich vielen Teilspektren hat nun eine andere Form. Wichtig ist nur das mittlere Spektrum um $f = 0$.
Alle anderen Spektralanteile werden empfängerseitig durch den Tiefpass der Signalrekonstruktion entfernt.
Verwendet man für diesen Tiefpass wieder ein Rechteckfilter mit der Verstärkung um $T_{\rm A}/T_{\rm R}$ im Durchlassbereich, so erhält man für das Ausgangsspektrum:

$$V(f) = Q(f) \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.05cm}.$$

$\text{Fazit:}$ Bei diskreter Abtastung und Rechteckfilterung kommt es zu Dämpfungsverzerrungen gemäß der Bewertungsfunktion ${\rm si}(πfT_{\rm R})$.

Diese sind um so stärker, je größer $T_{\rm R}$ ist. Nur im Grenzfall $T_{\rm R} → 0$ gilt ${\rm si}(πfT_{\rm R}) = 1$.
Allerdings können durch eine ideale Entzerrung diese linearen Dämpfungsverzerrungen vollständig kompensiert werden.
Um $V(f) = Q(f)$ bzw. $v(t) = q(t)$ zu erhalten, muss dann gelten:

$$H(f) = \left\{ \begin{array}{l} (T_{\rm A}/T_{\rm R})/{\rm si}(\pi f T_{\rm R}) \\ 0 \\ \end{array} \right.\quad\begin{array}{*{5}c}{\rm{f\ddot{u}r} }\\{\rm{f\ddot{u}r} } \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left \vert \hspace{0.005cm} f\hspace{0.05cm} \right \vert < f_{\rm A}/2}\hspace{0.05cm}, \\ {\hspace{0.04cm}\left \vert \hspace{0.005cm} f\hspace{0.05cm} \right \vert > f_{\rm A}/2}. \\ \end{array}$$

Quantisierung und Quantisierungsrauschen

Die zweite Funktionseinheit Quantisierung des PCM–Senders dient der Wertediskretisierung.

Hierzu wird der gesamte Wertebereich des analogen Quellensignals $($zum Beispiel der Bereich $± q_{\rm max})$ in $M$ Intervalle aufgeteilt.
Jedem Abtastwert $q_{\rm A}(ν · T_{\rm A})$ wird anschließend ein Repräsentant $q_{\rm Q}(ν · T_{\rm A})$ des zugehörigen Intervalls $($beispielsweise die Intervallmitte$)$ zugewiesen.

$\text{Beispiel 2:}$ Die Grafik verdeutlicht die Quantisierung am Beispiel der Quantisierungsstufenzahl $M = 8$.

Zur Verdeutlichung der Quantisierung mit $M = 8$ Stufen

Tatsächlich wird für $M$ in der Praxis wegen der anschließenden Binärcodierung stets eine Zweierpotenz gewählt.
Jeder der durch Kreise markierten Abtastwerte $q_{\rm A}(ν · T_{\rm A})$ wird durch den dazugehörigen quantisierten Wert $q_{\rm Q}(ν · T_{\rm A})$ ersetzt. Die quantisierten Werte sind als Kreuze eingetragen.
Dieser Vorgang der Wertdiskretisierung ist allerdings mit einer irreversiblen Verfälschung verbunden.
Die Verfälschung $ε_ν = q_{\rm Q}(ν · T_{\rm A}) \ - \ q_{\rm A}(ν · T_{\rm A})$ hängt von der Quantisierungsstufenzahl $M$ ab. Es gilt folgende Schranke:

$$\vert \varepsilon_{\nu} \vert < {1}/{2} \cdot2/M \cdot q_{\rm max}= {q_{\rm max} }/{M}\hspace{0.05cm}.$$

$\text{Definition:}$ Man bezeichnet das zweite Moment der Fehlergröße $ε_ν$ als Quantisierungsrauschleistung:

$$P_{\rm Q} = \frac{1}{2N+1 } \cdot\sum_{\nu = -N}^{+N}\varepsilon_{\nu}^2 \approx \frac{1}{N \cdot T_{\rm A} } \cdot \int_{0}^{N \cdot T_{\rm A} }\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.8cm} {\rm mit}\hspace{0.8cm}\varepsilon(t) = q_{\rm Q}(t) - q(t) \hspace{0.05cm}.$$

Anmerkungen:

Zur Berechnung der Quantisierungsrauschleistung $P_{\rm Q}$ wird meist die angegebene Näherung der „Spontanquantisierung” verwendet.
Man lässt dabei die Abtastung außer Betracht und bildet das Fehlersignal aus den zeitkontinuierlichen Signalen $q_{\rm Q}(t)$ und $q(t)$.
$P_{\rm Q}$ hängt auch vom Quellensignal $q(t)$ ab. Unter der Voraussetzung, dass $q(t)$ alle Werte zwischen $±q_{\rm max}$ mit gleicher Wahrscheinlichkeit annimmt und der Quantisierer genau für diesen Bereich ausgelegt ist, ergibt sich entsprechend Aufgabe 4.4:

$$P_{\rm Q} = \frac{q_{\rm max}^2}{3 \cdot M^2 } \hspace{0.05cm}.$$

Bei einem Sprach– oder Musiksignal können – wenn auch nur sehr selten – beliebig große Amplitudenwerte auftreten. In diesem Fall wird für $q_{\rm max}$ meist derjenige Amplitudenwert herangezogen, der nur zu $1\%$ aller Zeiten (betragsmäßig) überschritten wird.

PCM–Codierung und –Decodierung

Der Block PCM–Codierung dient der Umsetzung der zeitdiskreten $($nach Abtastung$)$ und wertdiskreten $($nach Quantisierung mit $M$ Stufen$)$ Signalwerte $q_{\rm Q}(ν · T_{\rm A})$ in eine Folge von $N = {\rm log_2}(M)$ Binärwerte. Logarithmus zur Basis 2 ⇒ "Logarithmus dualis".

$\text{Beispiel 3:}$ Jeder Binärwert ⇒ Bit ist durch ein Rechteck der Dauer $T_{\rm B} = T_{\rm A}/N$ dargestellt, woraus sich das Signal $q_{\rm C}(t)$ ergibt.

PCM–Codierung mit dem Dualcode $(M = 8,\ N = 3)$

Man erkennt:

Es wird hier der "Dualcode" verwendet. Das bedeutet, dass die Quantisierungsintervalle $\mu$ von $0$ bis $M–1$ durchnummeriert und anschließend in einfacher Binärform geschrieben werden. Mit $M = 8$ gilt beispielsweise $\mu = 6$ ⇔ 110.
Die drei Binärsymbole des codierten Signals $q_{\rm C}(t)$ ergeben sich, wenn man 0 durch L („Low”) und 1 durch H („High”) ersetzt. Im Beispiel erhält man so: HHL HHL LLH LHL HLH LHH.
Die Bitdauer $T_{\rm B}$ ist hier um den Faktor $N = {\rm log_2}(M) = 3$ kürzer als der Abtastabstand $T_{\rm A} = 1/f_{\rm A}$, und die Bitrate beträgt $R_{\rm B} = {\rm log_2}(M) · f_{\rm A}$.
Verwendet man bei der Decodierung $(v_{\rm C} ⇒ v_{\rm Q})$ die gleiche Zuordnung wie bei der Codierung $(q_{\rm Q} ⇒ q_{\rm C})$, so gilt stets, wenn man Übertragungsfehler ausschließt: $v_{\rm Q}(ν · T_{\rm A}) = q_{\rm Q}(ν · T_{\rm A}).$
Alternativ zum Dualcode ist der "Graycode" ⇒ benachbarte Binärwerte unterscheiden sich sich nur in einem Bit. Für $N = 3$:

$\mu = 0$: LLL, $\mu = 1$: LLH, $\mu = 2$: LHH, $\mu = 3$: LHL,

$\mu = 4$: HHL, $\mu = 5$: HHH, $\mu =6$: HLH, $\mu = 7$: HLL.

Signal–zu–Rausch–Leistungsverhältnis

Die digitale Pulscodemodulation $\rm (PCM)$ wird nun den analogen Modulationsverfahren $\rm (AM, \ FM)$ hinsichtlich des erreichbaren Sinken–SNR $ρ_v = P_q/P_ε$ bei AWGN–Rauschen vergleichend gegenüber gestellt.

Sinken–SNR bei AM, FM, PCM 30/32

Wie in vorherigen Kapiteln (zum Beispiel) bezeichnet $ξ = {α_{\rm K} }^2 · P_{\rm S}/(N_0 · B_{\rm NF})$ die Leistungskenngröße. Diese fasst verschiedene Einflüsse zusammen:

den Kanalübertragungsfaktor $α_{\rm K}$ (quadratisch),
die Sendeleistung $P_{\rm S}$,
die AWGN–Rauschleistungsdichte $N_0$ (reziprok) sowie
die Signalbandbreite $B_{\rm NF}$ (ebenfalls reziprok); bei einer harmonischen Schwingung: Frequenz $f_{\rm N}$ statt $B_{\rm NF}$.

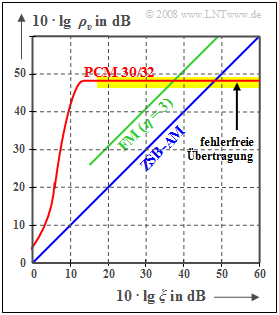
Die beiden Vergleichskurven für Amplitudenmodulation und für Frequenzmodulation kann man wie folgt beschreiben:

Zweiseitenband–AM $\text{(ZSB–AM)}$ ohne Träger $(m \to \infty)$:

$$ρ_v = ξ \ ⇒ \ 10 · \lg ρ_v = 10 · \lg \ ξ,$$

Frequenzmodulation $\text{(FM)}$ mit Modulationsindex $η = 3$:

$$ρ_υ = 3/2 \cdot η^2 · ξ = 13.5 · ξ \ ⇒ \ 10 · \lg \ ρ_v = 10 · \lg \ ξ + 11.3 \ \rm dB.$$

Die Kurve für das $\text{PCM 30/32}$ ist wie folgt zu interpretieren:

Ist die Leistungskenngröße $ξ$ hinreichend groß, so treten keine Übertragungsfehler auf. Das Fehlersignal $ε(t) = v(t) \ - \ q(t)$ ist dann allein auf die Quantisierung zurückzuführen $(P_ε = P_{\rm Q})$.
Mit der Quantisierungsstufenzahl $M = 2^N$ gilt in diesem Fall näherungsweise:

$$\rho_{v} = \frac{P_q}{P_\varepsilon}= M^2 = 2^{2N} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{v}=20 \cdot {\rm lg}\hspace{0.1cm}M = N \cdot 6.02\,{\rm dB}$$

$$ \Rightarrow \hspace{0.3cm} N = 8, \hspace{0.05cm} M =256\text{:}\hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{v}=48.16\,{\rm dB}\hspace{0.05cm}.$$

Anzumerken ist, dass die angegebene Gleichung nur für ein sägezahnförmiges Quellensignal exakt gültig ist. Bei cosinusförmigem Quellensignal ist jedoch die Abweichung hiervon nicht sehr groß.
Mit kleiner werdendem $ξ$ $($kleinere Sendeleistung oder größere Rauschleistungsdichte$)$ nehmen die Übertragungsfehler zu. Damit wird $P_ε > P_{\rm Q}$ und der Sinken–Störabstand wird kleiner.
Die PCM $($mit $M = 256)$ ist den Analogverfahren $($AM und FM$)$ nur im unteren und mittleren $ξ$–Bereich überlegen. Spielen aber Übertragungsfehler keine Rolle mehr, so ist durch ein größeres $ξ$ keine Verbesserung mehr zu erzielen $($horizontaler, gelb hinterlegter Kurvenabschnitt$)$.
Eine Verbesserung bringt dann nur eine Erhöhung von $N$ $($Bitanzahl pro Abtastwert$)$ ⇒ größeres $M = 2^N$ $($Quantisierungsstufenzahl$)$. Beispielsweise erreicht man bei einer Compact Disc $($CD$)$ mit dem Parameter $N = 16$ ⇒ $M = 65536$ den Wert

$$10 · \lg \ ρ_v = 96.32 \ \rm dB.$$

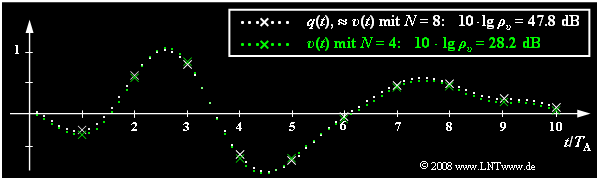
$\text{Beispiel 4:}$ Die folgende Grafik zeigt den begrenzenden Einfluss der Quantisierung:

Weiß gepunktet dargestellt ist das Quellensignal $q(t)$, grün gepunktet das Sinkensignal $v(t)$ nach einer PCM mit $N = 4$ ⇒ $M = 16$.
Die Abtastzeitpunkte sind durch Kreuze markiert.
Übertragungsfehler werden vorerst ausgeschlossen. Abtastung und Signalrekonstruktion seien bestmöglich an das Quellensignal $q(t)$ angepasst.

Dieses Bild kann wie folgt interpretiert werden:

Einfluss der Quantisierung mit $N = 4$ und $N = 8$

Mit $N = 8$ ⇒ $M = 256$ ist das Sinkensignal $v(t)$ vom Quellensignal $q(t)$ mit dem bloßen Auge nicht unterscheidbar. Für beide gilt näherungsweise der weiß gepunktete Verlauf.
Am Störabstand $10 · \lg \ ρ_v = 47.8 \ \rm dB$ erkennt man aber, dass das Quantisierungsrauschen $($Leistung $P_\varepsilon$ des Fehlersignals$)$ nur etwa um den Faktor $1.6 · 10^{–5}$ kleiner ist als die Leistung $P_q$ des Quellensignals. Dieses SNR wäre bei einem Sprach– oder Musiksignal schon deutlich hörbar.
Obwohl das betrachtete Quellensignal weder sägezahnförmig noch cosinusförmig verläuft, sondern sich aus mehreren Frequenzanteilen zusammensetzt, weicht die angegebene Näherung $ρ_v ≈ M^2$ ⇒ $10 · \lg \ ρ_υ = 48.16 \ \rm dB$ nur unwesentlich vom tatsächlichen Wert ab.
Dagegen erkennt man für $N = 4$ ⇒ $M = 16$ bereits im Bild Abweichungen zwischen dem Sinkensignal $($grün markiert$)$ und dem Quellensignal $($weiße Markierung$)$, was auch durch den kleinen Störabstand $10 · \lg \ ρ_υ = 28.2 \ \rm dB$ quantitativ zum Ausdruck kommt.

Einfluss von Übertragungsfehlern

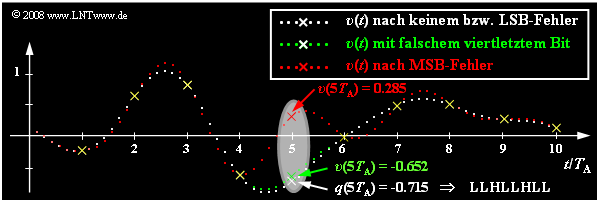
Ausgehend vom gleichen Analogsignal $q(t)$ wie im letzten Abschnitt und einer linearen Quantisierung mit $N = 8$ Bit ⇒ $M = 256$ werden nun die Auswirkungen von Übertragungsfehlern anhand des jeweiligen Sinkensignals $v(t)$ verdeutlicht.

Einfluss eines Übertragungsfehlers bezüglich Bit 5 beim Dualcode, was bedeutet, dass das niedrigste Quantisierungsintervall $(\mu = 0)$ mit LLLL LLLL' und das höchste Intervall $(\mu = 255)$ mit HHHH HHHH dargestellt wird

Tabelle mit den Ergebnissen der Bitfehleranalyse. $10 · \lg \ ρ_v$ wurde aus dem dargestellten (sehr kurzen) Signalausschnitt der Dauer $10 · T_{\rm A}$ berechnet. Bei jeweils nur einem Fehler bei der Übertragung von $10 · 8 = 80$ Bit ergibt dies bereits die Bitfehlerrate $1.25\%$

Die weißen Punkte markieren wieder das Quellensignal $q(t)$. Ohne Übertragungsfehler hat das Sinkensignal $v(t)$ bei Vernachlässigung der Quantisierung den gleichen Verlauf.
Nun wird jeweils genau ein Bit des fünften Abtastwertes $q(5 · T_{\rm A}) = -0.715$ verfälscht, wobei dieser Abtastwert mit LLHL LHLL codiert wurde.

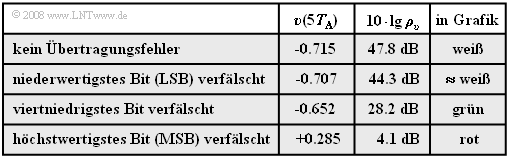
Die in der Grafik und der Tabelle dargestellten Ergebnisse dieser Fehleranalyse können wie folgt zusammengefasst werden:

Wird nur das letzte Bit des Binärwortes verfälscht $\rm (LSB$: "Least Significant Bit", LLHL LHLL ⇒ LLHL LHLH$)$, so ist mit bloßem Auge kein Unterschied zur fehlerfreien Übertragung zu erkennen $($weißer Kurvenzug$)$. Trotzdem ist der Störabstand $3.5 \ \rm dB$ kleiner.
Ein Übertragungsfehler des viertletzten Bits $($grüne Kurve, LLHLLHLL ⇒ LLHLHHLL$)$ führt bereits zu einer deutlich erkennbaren Verfälschung um acht Quantisierungsintervalle. Das heißt: $v(5T_{\rm A}) \ - \ q(5T_{\rm A}) = 8/256 · 2 = 0.0625$ und der Störabstand sinkt auf $10 · \lg \ ρ_υ = 28.2 \ \rm dB$.
Die rote Kurve zeigt schließlich den Fall, dass das $\rm MSB$ ("Most Significant Bit") verfälscht wird: LLHLLHLL ⇒ HLHLLHLL. Dies führt zur Verfälschung $v(5T_{\rm A}) \ – \ q(5T_{\rm A}) = 1$ (entspricht dem halben Aussteuerbereich). Der Störabstand beträgt nun nur mehr etwa $4 \ \rm dB$.
Zu allen Abtastzeitpunkten mit Ausnahme von $5T_{\rm A}$ stimmt $v(t)$ bis auf den Quantisierungsfehler mit $q(t)$ exakt überein. Außerhalb dieser durch gelbe Kreuze markierten Zeiten führt der einzige Fehler bei $5T_{\rm A}$ aber in einem ausgedehnten Bereich zu starken Abweichungen, was auf die Interpolation mit der $\rm si$–förmigen Impulsantwort des Rekonstruktionstiefpasses $H(f)$ zurückzuführen ist.

Abschätzung der SNR-Degradation durch Übertragungsfehler

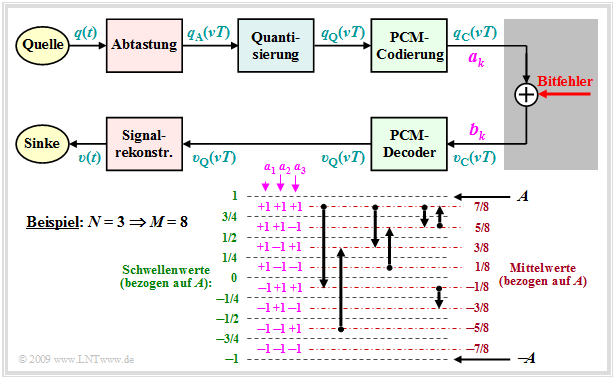
Nun soll versucht werden, die SNR–Kurve des PCM–Systems unter Berücksichtigung von Bitfehlern zumindest näherungsweise zu bestimmen. Wir gehen dabei vom folgenden Blockschaltbild aus und setzen weiter voraus:

Zur Berechnung des PCM–SNR mit Berücksichtigung von Bitfehlern

Jeder Abtastwert $q_{\rm A}(νT)$ wird mit $M$ Stufen quantisiert und mit $N = {\rm log_2} (M)$ Bit dargestellt. Im Bild: $M = 8$ ⇒ $N = 3$.
Die Binärform von $q_{\rm Q}(νT)$ liefert die Amplitudenkoeffizienten $a_k\, (k = 1, \text{...} \hspace{0.08cm}, N)$, die durch Bitfehler in die Koeffizienten $b_k$ verfälscht werden. Sowohl $a_k$ als auch $b_k$ sind jeweils $±1$.
Ein Fehler $(b_k ≠ a_k)$ tritt mit Wahrscheinlichkeit $p_{\rm B}$ auf. Jedes Bit wird gleichwahrscheinlich verfälscht und in jedem PCM–Wort ist maximal ein Fehler ⇒ nur eines der $N$ Bit kann falsch sein.

Aus dem in der Grafik angegebenen Diagramm ist für $N = 3$ und natürliche Binärcodierung ("Dualcode") zu erkennen:

Eine Verfälschung von $a_1$ verändert $q_{\rm Q}(νT)$ um $±A$.
Eine Verfälschung von $a_2$ verändert $q_{\rm Q}(νT)$ um $±A/2.$
Eine Verfälschung von $a_3$ verändert $q_{\rm Q}(νT)$ um $±A/4$.

Für den Fall, dass (nur) der Koeffizient $a_k$ gefälscht wurde, erhalten wir durch Verallgemeinerung für die Abweichung:

$$\varepsilon_k = υ_{\rm Q}(νT) \ - \ q_{\rm Q}(νT)= - a_k \cdot A \cdot 2^{-k +1} \hspace{0.05cm}.$$

Für die Fehlerrauschleistung erhält man nach Mittelung über alle Verfälschungswerte $ε_k$ (mit $1 ≤ k ≤ N)$ unter Berücksichtigung der Bitfehlerwahrscheinlichkeit $p_{\rm B}$:

$$P_{\rm F}= {\rm E}\big[\varepsilon_k^2 \big] = \sum\limits^{N}_{k = 1} p_{\rm B} \cdot \left ( - a_k \cdot A \cdot 2^{-k +1} \right )^2 =\ p_{\rm B} \cdot A^2 \cdot \sum\limits^{N-1}_{k = 0} 2^{-2k } = p_{\rm B} \cdot A^2 \cdot \frac{1- 2^{-2N }}{1- 2^{-2 }} \approx {4}/{3} \cdot p_{\rm B} \cdot A^2 \hspace{0.05cm}.$$

Hierbei ist die Summenformel der geometrischen Reihe sowie die Näherung $1 – 2^{–2N } ≈ 1$ verwendet.
Für $N = 8$ ⇒ $M = 256$ beträgt der damit verbundene relative Fehler beispielsweise etwa $\rm 10^{–5}$.

Ohne Berücksichtigung von Übertragungsfehlern hat sich für das Signal–zu–Rausch–Leistungsverhältnis $ρ_v = P_{\rm S}/P_{\rm Q}$ ergeben, wobei bei einem gleichverteilten Quellensignal (zum Beispiel sägezahnförmig) die Signalleistung und die Quantisierungsrauschleistung wie folgt zu berechnen ist:

$$P_{\rm S}={A^2}/{3}\hspace{0.05cm},\hspace{0.3cm}P_{\rm Q}= {A^2}/{3} \cdot 2^{-2N } \hspace{0.05cm}.$$

Sinken–SNR für PCM unter Berücksichtigung von Bitfehlern

Unter Berücksichtigung der Übertragungsfehler erhält man mit obigem Ergebnis:

$$\rho_{\upsilon}= \frac{P_{\rm S}}{P_{\rm Q}+P_{\rm F}} = \frac{A^2/3}{A^2/3 \cdot 2^{-2N } + A^2/3 \cdot 4 \cdot p_{\rm B}} = \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$

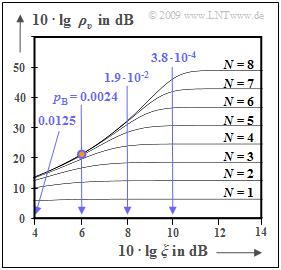
Die Grafik zeigt $10 · \lg ρ_v$ in Abhängigkeit der (logarithmierten) Leistungskenngröße $ξ = P_{\rm S}/(N_0 · B_{\rm NF})$, wobei $B_{\rm NF}$ die Signalbandbreite angibt. Der konstante Kanalübertragungsfaktor sei idealerweise $α_{\rm K} = 1$.

Beim optimalen Binärsystem und AWGN–Rauschen gilt aber für die Leistungskenngröße auch $ξ = E_{\rm B}/N_0$
$($Energie pro Bit bezogen auf die Rauschleistungsdichte$)$.
Die Bitfehlerwahrscheinlichkeit ist dann mit der Gaußschen Fehlerfunktion ${\rm Q}(x)$ wie folgt gegeben:

$$p_{\rm B}= {\rm Q} \left ( \sqrt{{2E_{\rm B}}/{N_0} }\right ) \hspace{0.05cm}.$$

Für $N = 8$ ⇒ $ 2^{–2{\it N} } = 1.5 · 10^{–5}$ sowie $10 · \lg \ ξ = 6 \ \rm dB$ ⇒ $p_{\rm B} = 0.0024$ $($rot markierter Punkt$)$ ergibt sich:

$$\rho_{\upsilon}= \frac{1}{ 1.5 \cdot 10^{-5} + 4 \cdot 0.0024} \approx 100 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\upsilon}\approx 20\,{\rm dB} \hspace{0.05cm}.$$

Dieser kleine $ρ_v$–Wert geht auf den Term $4 · 0.0024$ im Nenner $($Einfluss des Übertragungsfehlers$)$ zurück,
während im horizontalen Kurvenabschnitt für jedes $N$ $($Bitanzahl pro Abtastwert$)$ der Term $\rm 2^{–2{\it N} }$ dominiert – also das Quantisierungsrauschen.

Nichtlineare Quantisierung

Häufig werden die Quantisierungsintervalle nicht gleich groß gewählt, sondern man verwendet für den inneren Amplitudenbereich eine feinere Quantisierung als für große Amplituden. Dafür gibt es mehrere Gründe: Wahrscheinlichkeitsdichtefunktion.

Ungleichmäßige Quantisierung eines Sprachsignals

Bei Audiosignalen werden Verfälschungen der leisen Signalanteile (also Werte in der Nähe der Nulllinie) subjektiv als störender empfunden als eine Beeinträchtigung großer Amplitudenwerte.
Eine solche ungleichmäßige Quantisierung führt bei einem solchen Musik– oder Sprachsignal auch zu einem größeren Sinkenstörabstand, da hier die Signalamplitude nicht gleichverteilt ist.

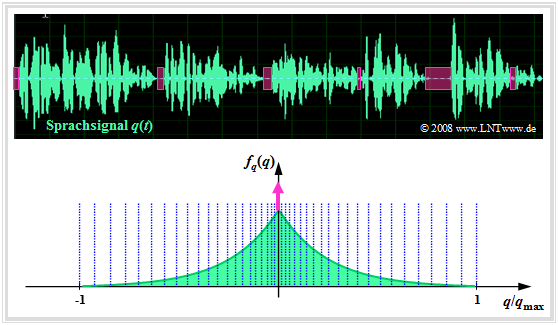
Die Grafik zeigt ein Sprachsignal $q(t)$ und dessen Amplitudenverteilung $f_q(q)$ ⇒ Es handelt sich um die Laplaceverteilung, die man wie folgt annähern kann:

durch eine kontinuierliche, zweiseitige Exponentialverteilung, und
durch eine Diracfunktion $δ(q)$ zur Berücksichtigung der Sprachpausen (magentafarben).

In der Grafik ist die nichtlineare Quantisierung nur angedeutet, zum Beispiel mittels der 13–Segment–Kennlinie, die in der Aufgabe 4.5 genauer beschrieben ist:

Die Quantisierungsintervalle werden hierbei zu den Rändern hin abschnittsweise immer breiter.
Die häufigeren kleinen Amplituden werden dagegen sehr fein quantisiert.

Kompression und Expandierung

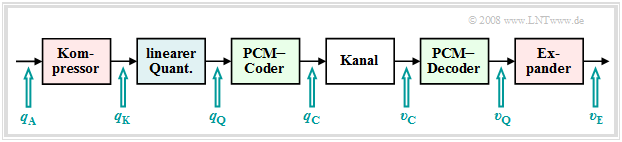
Eine ungleichmäßige Quantisierung kann zum Beispiel dadurch realisiert werden, in dem

die abgetasteten Werte $q_{\rm A}(ν · T_{\rm A})$ zunächst durch eine nichtlineare Kennlinie $q_{\rm K}(q_{\rm A})$ verformt und
anschließend die entstehenden Ausgangswerte $q_{\rm K}(ν · T_{\rm A})$ gleichmäßig quantisiert werden.

Realisierung einer ungleichmäßigen Quantisierung

Damit ergibt sich die nebenstehend skizzierte Signalkette.

$\text{Fazit:}$ Eine solche ungleichmäßige Quantisierung bedeutet:

Durch die nichtlineare Kennlinie $q_{\rm K}(q_{\rm A})$ werden kleine Signalwerte verstärkt und große Werte abgeschwächt ⇒ Kompression.
Diese bewusste Signalverzerrung macht man beim Empfänger durch die Umkehrfunktion $v_{\rm E}(υ_{\rm Q})$ rückgängig ⇒ Expandierung.
Den Gesamtvorgang von sendeseitiger Kompression und empfängerseitiger Expansion nennt man auch Kompandierung.

Für das PCM–System 30/32 wurde von der Comité Consultatif International des Télégraphique et Téléphonique (CCITT) die so genannte A–Kennlinie empfohlen:

$$y(x) = \left\{ \begin{array}{l} \frac{1 + {\rm ln}(A \cdot x)}{1 + {\rm ln}(A)} \\ \frac{A \cdot x}{1 + {\rm ln}(A)} \\ - \frac{1 + {\rm ln}( - A \cdot x)}{1 + {\rm ln}(A)} \\ \end{array} \right.\quad\begin{array}{*{5}c}{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}}\\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c}1/A \le x \le 1\hspace{0.05cm}, \\ - 1/A \le x \le 1/A\hspace{0.05cm}, \\ - 1 \le x \le - 1/A\hspace{0.05cm}. \\ \end{array}$$

Hierbei ist zur Abkürzung $x = q_{\rm A}(ν · T_{\rm A})$ und $y = q_{\rm K}(ν · T_{\rm A})$ verwendet.
Diese Kennlinie mit dem in der Praxis eingeführten Wert $A = 87.56$ hat eine sich ständig ändernde Steigung.
Nähere Angaben zu dieser Art der ungleichmäßigen Quantisierung finden Sie in der Aufgabe 4.5.

Hinweis: Im dritten Teil des Lernvideos Pulscodemodulation werden behandelt:

die Definition des Signal–zu–Rausch–Leistungsverhältnisses (SNR),
der Einfluss von Quantisierungsrauschen und Übertragungsfehlern,
die Unterschiede zwischen linearer und nichtlinearer Quantisierung.

Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im

Kapitel 12: Pulscodemodulation, Programm pcm

des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms;
dieser Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 12: Seite 271-294.

Aufgaben zum Kapitel

Aufgabe 4.1: PCM–System 30/32

Aufgabe 4.2: Tiefpass zur Signalrekonstruktion

Aufgabe 4.2Z: Zum Abtasttheorem

Aufgabe 4.3: Natürliche und diskrete Abtastung

Aufgabe 4.4: Zum Quantisierungsrauschen

Aufgabe 4.4Z: Störabstand bei PCM

Aufgabe 4.5: Nichtlineare Quantisierung

Aufgabe 4.6: Quantisierungskennlinien