Signaldarstellung/Gleichsignal - Grenzfall eines periodischen Signals: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Ein | + | Ein $\text{Gleichsignal}$ ist ein deterministisches Signal, dessen Augenblickswerte für alle Zeiten $t$ von $-\infty$ bis $+\infty$ konstant sind. Ein solches Signal ist der Grenzfall einer [[Signaldarstellung/Harmonische_Schwingung|harmonischen Schwingung]], wobei die Periodendauer $T_{0}$ einen unendlich großen Wert besitzt.}} |
[[Datei:Sig_T_2_2_S1a_Version2.png|right|frame|Gleichsignal im Zeitbereich]] | [[Datei:Sig_T_2_2_S1a_Version2.png|right|frame|Gleichsignal im Zeitbereich]] | ||
| − | Entsprechend dieser Definition reicht ein Gleichsignal immer von $t = -\infty$ bis $t = +\infty$. | + | Entsprechend dieser Definition reicht ein Gleichsignal immer von $t = -\infty$ bis $t = +\infty$. |
| − | Wird das Signal erst zum Zeitpunkt $t = 0$ eingeschaltet, so liegt kein Gleichsignal vor. | + | Wird das Signal erst zum Zeitpunkt $t = 0$ eingeschaltet, so liegt also kein Gleichsignal vor. |
| − | *Ein Gleichsignal kann niemals Träger von Information im nachrichtentechnischen Sinne sein, doch können Nachrichtensignale durchaus einen | + | *Ein Gleichsignal kann niemals Träger von Information im nachrichtentechnischen Sinne sein, doch können Nachrichtensignale durchaus einen „Gleichsignalanteil” besitzen. |
*Alle im Folgenden für das Gleichsignal getroffenen Aussagen gelten in gleicher Weise auch für einen solchen Gleichsignalanteil. | *Alle im Folgenden für das Gleichsignal getroffenen Aussagen gelten in gleicher Weise auch für einen solchen Gleichsignalanteil. | ||
<br clear=all> | <br clear=all> | ||
| Zeile 23: | Zeile 23: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Für den | + | Für den $\text{Gleichsignalanteil}$ $A_{0}$ eines beliebigen Signals $x(t)$ gilt: |
:$$A_0 = \lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\,{\rm d} t. $$ | :$$A_0 = \lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\,{\rm d} t. $$ | ||
| Zeile 41: | Zeile 41: | ||
==Spektraldarstellung== | ==Spektraldarstellung== | ||
<br> | <br> | ||
| − | Wir betrachten nun den Sachverhalt im Frequenzbereich. Aus der Zeitfunktion ist bereits ersichtlich, dass diese – spektral gesehen – nur eine einzige (physikalische) Frequenz beinhaltet, nämlich die Frequenz $f=0$. | + | Wir betrachten nun den Sachverhalt im Frequenzbereich. Aus der Zeitfunktion ist bereits ersichtlich, dass diese – spektral gesehen – nur eine einzige (physikalische) Frequenz beinhaltet, nämlich die Frequenz $f=0$. |
| − | Dieses Ergebnis soll nun mathematisch hergeleitet werden. | + | Dieses Ergebnis soll nun mathematisch hergeleitet werden. |
Im Vorgriff auf das Kapitel [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Fouriertransformation]] wird bereits hier der Zusammenhang zwischen dem Zeitsignal $x(t)$ und dem korrespondierenden Spektrum $X(f)$ angegeben: | Im Vorgriff auf das Kapitel [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Fouriertransformation]] wird bereits hier der Zusammenhang zwischen dem Zeitsignal $x(t)$ und dem korrespondierenden Spektrum $X(f)$ angegeben: | ||
| Zeile 59: | Zeile 59: | ||
mit folgenden Eigenschaften: | mit folgenden Eigenschaften: | ||
| − | *Das Integral divergiert für $f=0$, das heißt, es liefert einen unendlich großen Wert (Integration über den konstanten Wert 1). | + | *Das Integral divergiert für $f=0$, das heißt, es liefert einen unendlich großen Wert $($Integration über den konstanten Wert $1)$. |
| − | *Für eine Frequenz $f\ne 0$ ist das Integral dagegen Null; der dazugehörige Beweis ist allerdings nicht trivial (siehe nächste Seite). | + | *Für eine Frequenz $f\ne 0$ ist das Integral dagegen Null; der dazugehörige Beweis ist allerdings nicht trivial $($siehe nächste Seite$)$. |
| Zeile 69: | Zeile 69: | ||
:$$X(f) = A_0 \, \cdot \, \rm \delta(\it f).$$ | :$$X(f) = A_0 \, \cdot \, \rm \delta(\it f).$$ | ||
| − | *Man bezeichnet $\delta(f)$ als | + | *Man bezeichnet $\delta(f)$ als $\text{Diracfunktion}$, auch bekannt unter dem Namen „Distribution”. |
| − | *$\delta(f)$ ist eine mathematisch komplizierte Funktion; die Herleitung finden Sie auf der nächsten Seite.}} | + | *$\delta(f)$ ist eine mathematisch komplizierte Funktion; die Herleitung finden Sie auf der nächsten Seite.}} |
| Zeile 88: | Zeile 88: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Die für die funktionale Beschreibung von nachrichtentechnischen Systemen äußerst wichtige | + | Die für die funktionale Beschreibung von nachrichtentechnischen Systemen äußerst wichtige $\text{Diracfunktion}$ weist folgende Eigenschaften auf: |
*Die Diracfunktion ist unendlich schmal, das heißt, es ist $\delta(f)=0$ für $f \neq 0$. | *Die Diracfunktion ist unendlich schmal, das heißt, es ist $\delta(f)=0$ für $f \neq 0$. | ||
*Die Diracfunktion $\delta(f)$ ist bei der Frequenz $f = 0$ unendlich hoch. | *Die Diracfunktion $\delta(f)$ ist bei der Frequenz $f = 0$ unendlich hoch. | ||
| Zeile 101: | Zeile 101: | ||
Zur mathematischen Herleitung obiger Eigenschaften gehen wir von einem dimensionslosen Gleichsignal aus. | Zur mathematischen Herleitung obiger Eigenschaften gehen wir von einem dimensionslosen Gleichsignal aus. | ||
| − | Um die Konvergenz des Fourierintegrals zu erzwingen, wird das nicht energiebegrenzte Signal $x(t)$ mit einer beidseitig abfallenden Exponentialfunktion multipliziert. Die Grafik zeigt das Signal $x(t)=1$ und das energiebegrenzte Signal | + | *Um die Konvergenz des Fourierintegrals zu erzwingen, wird das nicht energiebegrenzte Signal $x(t)$ mit einer beidseitig abfallenden Exponentialfunktion multipliziert. Die Grafik zeigt das Signal $x(t)=1$ und das energiebegrenzte Signal |
:$$x_{\varepsilon} (t) = \rm e^{\it -\varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.01cm} t \hspace{0.01cm}\vert}{.}$$ | :$$x_{\varepsilon} (t) = \rm e^{\it -\varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.01cm} t \hspace{0.01cm}\vert}{.}$$ | ||
| − | Hierbei gelte $\varepsilon > 0$. Im Grenzübergang $\varepsilon \to 0$ geht $x_{\varepsilon}(t)$ in $x(t)=1$ über. | + | :Hierbei gelte $\varepsilon > 0$. Im Grenzübergang $\varepsilon \to 0$ geht $x_{\varepsilon}(t)$ in $x(t)=1$ über. |
| − | Zur Spektraldarstellung kommt man durch Anwendung des vorne angegebenen Fourierintegrals: | + | *Zur Spektraldarstellung kommt man durch Anwendung des vorne angegebenen Fourierintegrals: |
:$$X_\varepsilon (f)=\int_{-\infty}^{0} {\rm e}^{\varepsilon{t} }\, {\cdot}\, {\rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t \hspace{0.2cm}+ \hspace{0.2cm} \int_{0}^{+\infty} {\rm e}^{-\varepsilon t} \,{\cdot}\, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$ | :$$X_\varepsilon (f)=\int_{-\infty}^{0} {\rm e}^{\varepsilon{t} }\, {\cdot}\, {\rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t \hspace{0.2cm}+ \hspace{0.2cm} \int_{0}^{+\infty} {\rm e}^{-\varepsilon t} \,{\cdot}\, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$ | ||
| − | Nach Integration und Zusammenfassen beider Anteile erhalten wir die rein reelle Spektralfunktion des energiebegrenzten Signals $x_{\varepsilon}(t)$: | + | *Nach Integration und Zusammenfassen beider Anteile erhalten wir die rein reelle Spektralfunktion des energiebegrenzten Signals $x_{\varepsilon}(t)$: |
:$$X_\varepsilon (f)=\frac{1}{\varepsilon -\rm j \cdot 2\pi \it f} + \frac{1}{\varepsilon+\rm j \cdot 2\pi \it f} = \frac{2\varepsilon}{\varepsilon^2 + (\rm 2\pi {\it f}\hspace{0.05cm} ) \rm ^2} \, .$$ | :$$X_\varepsilon (f)=\frac{1}{\varepsilon -\rm j \cdot 2\pi \it f} + \frac{1}{\varepsilon+\rm j \cdot 2\pi \it f} = \frac{2\varepsilon}{\varepsilon^2 + (\rm 2\pi {\it f}\hspace{0.05cm} ) \rm ^2} \, .$$ | ||
| − | Die Fläche unter der $X_\varepsilon (f)$–Kurve ist unabhängig vom Parameter $\varepsilon$ gleich $1$. Je kleiner $ε$ gewählt wird, um so schmaler und höher wird die Funktion, wie das Lernvideo [[Herleitung_und_Visualisierung_der_Diracfunktion_(Lernvideo)|Herleitung und Visualisierung der Diracfunktion]] zeigt. | + | *Die Fläche unter der $X_\varepsilon (f)$–Kurve ist unabhängig vom Parameter $\varepsilon$ gleich $1$. Je kleiner $ε$ gewählt wird, um so schmaler und höher wird die Funktion, wie das Lernvideo [[Herleitung_und_Visualisierung_der_Diracfunktion_(Lernvideo)|Herleitung und Visualisierung der Diracfunktion]] zeigt. |
| − | Der Grenzübergang für $\varepsilon \to 0$ liefert die Diracfunktion mit dem Gewicht $1$: | + | *Der Grenzübergang für $\varepsilon \to 0$ liefert die Diracfunktion mit dem Gewicht $1$: |
:$$\lim_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm} 0}X_\varepsilon (f)= \delta(f).$$}} | :$$\lim_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm} 0}X_\varepsilon (f)= \delta(f).$$}} | ||
Version vom 12. April 2021, 14:25 Uhr
Inhaltsverzeichnis
Zeitsignaldarstellung
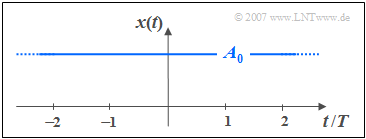
$\text{Definition:}$ Ein $\text{Gleichsignal}$ ist ein deterministisches Signal, dessen Augenblickswerte für alle Zeiten $t$ von $-\infty$ bis $+\infty$ konstant sind. Ein solches Signal ist der Grenzfall einer harmonischen Schwingung, wobei die Periodendauer $T_{0}$ einen unendlich großen Wert besitzt.
Entsprechend dieser Definition reicht ein Gleichsignal immer von $t = -\infty$ bis $t = +\infty$. Wird das Signal erst zum Zeitpunkt $t = 0$ eingeschaltet, so liegt also kein Gleichsignal vor.
- Ein Gleichsignal kann niemals Träger von Information im nachrichtentechnischen Sinne sein, doch können Nachrichtensignale durchaus einen „Gleichsignalanteil” besitzen.
- Alle im Folgenden für das Gleichsignal getroffenen Aussagen gelten in gleicher Weise auch für einen solchen Gleichsignalanteil.
$\text{Definition:}$ Für den $\text{Gleichsignalanteil}$ $A_{0}$ eines beliebigen Signals $x(t)$ gilt:
- $$A_0 = \lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\,{\rm d} t. $$
- Die Messdauer $T_{\rm M}$ sollte stets möglichst groß gewählt werden (im Grenzfall unendlich).
- Die angegebene Gleichung gilt allerdings nur dann, wenn $T_{\rm M}$ symmetrisch um den Zeitpunkt $t=0$ liegt.
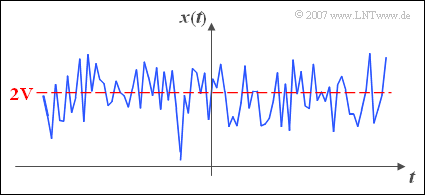
$\text{Beispiel 1:}$ Die Grafik zeigt ein stochastisches Signal $x(t)$.
- Der Gleichsignalanteil $A_{0}$ ist hierbei $2\ \rm V$.
- Im Sinne der Statistik entspricht $A_{0}$ dem linearen Mittelwert.
Spektraldarstellung
Wir betrachten nun den Sachverhalt im Frequenzbereich. Aus der Zeitfunktion ist bereits ersichtlich, dass diese – spektral gesehen – nur eine einzige (physikalische) Frequenz beinhaltet, nämlich die Frequenz $f=0$.
Dieses Ergebnis soll nun mathematisch hergeleitet werden. Im Vorgriff auf das Kapitel Fouriertransformation wird bereits hier der Zusammenhang zwischen dem Zeitsignal $x(t)$ und dem korrespondierenden Spektrum $X(f)$ angegeben:
- $$X(f)= \hspace{0.05cm}\int_{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$
Man bezeichnet die so berechnete Spektralfunktion $X(f)$ nach dem französischen Mathematiker Jean Baptiste Joseph Fourier als die Fouriertransformierte von $x(t)$ und verwendet als Kurzbezeichnung für diesen Funktionalzusammenhang
- $$X(f)\ \bullet\!\!-\!\!\!-\!\!\circ\,\ x(t).$$
Beschreibt $x(t)$ beispielsweise einen Spannungsverlauf, so hat $X(f)$ die Einheit „V/Hz“.
Wendet man diese Transformationsgleichung auf das Gleichsignal $x(t)=A_{0}$ an, so erhält man die Spektralfunktion
- $$X(f)= A_0 \cdot \int_{-\infty} ^{+\hspace{0.01cm}\infty}\rm e \it ^{-\rm {j 2\pi} \it ft} \,{\rm d}t.$$
mit folgenden Eigenschaften:
- Das Integral divergiert für $f=0$, das heißt, es liefert einen unendlich großen Wert $($Integration über den konstanten Wert $1)$.
- Für eine Frequenz $f\ne 0$ ist das Integral dagegen Null; der dazugehörige Beweis ist allerdings nicht trivial $($siehe nächste Seite$)$.
$\text{Definition:}$ Die gesuchte Spektralfunktion $X(f)$ wird kompakt durch folgende Gleichung ausgedrückt:
- $$X(f) = A_0 \, \cdot \, \rm \delta(\it f).$$
- Man bezeichnet $\delta(f)$ als $\text{Diracfunktion}$, auch bekannt unter dem Namen „Distribution”.
- $\delta(f)$ ist eine mathematisch komplizierte Funktion; die Herleitung finden Sie auf der nächsten Seite.
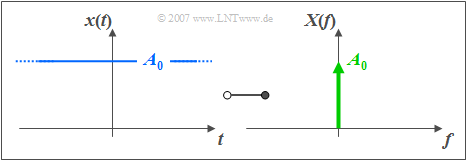
$\text{Beispiel 2:}$ Die Grafik zeigt den Funktionalzusammenhang
- zwischen einem Gleichsignal $x(t)=A_{0}$ und
- der dazugehörigen Spektralfunktion $X(f)=A_{0} \cdot \delta(f)$.
Die Diracfunktion bei der Frequenz $f=0$ ist durch einen Pfeil dargestellt, der mit dem Gewicht $A_{0}$ versehen ist.
Diracfunktion im Frequenzbereich
$\text{Definition:}$ Die für die funktionale Beschreibung von nachrichtentechnischen Systemen äußerst wichtige $\text{Diracfunktion}$ weist folgende Eigenschaften auf:
- Die Diracfunktion ist unendlich schmal, das heißt, es ist $\delta(f)=0$ für $f \neq 0$.
- Die Diracfunktion $\delta(f)$ ist bei der Frequenz $f = 0$ unendlich hoch.
- Die Impulsfläche der Diracfunktion ergibt einen endlichen Wert, nämlich $1$:
- $$\int_\limits{-\infty} ^{+\infty} \delta( f)\,{\rm d}f =1.$$
- Aus dieser letzten Eigenschaft folgt, dass $\delta(f)$ die Einheit ${\rm Hz}^{-1} = {\rm s}$ besitzt.
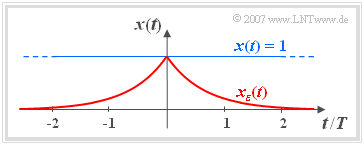
$\text{Beweis:}$ Zur mathematischen Herleitung obiger Eigenschaften gehen wir von einem dimensionslosen Gleichsignal aus.
- Um die Konvergenz des Fourierintegrals zu erzwingen, wird das nicht energiebegrenzte Signal $x(t)$ mit einer beidseitig abfallenden Exponentialfunktion multipliziert. Die Grafik zeigt das Signal $x(t)=1$ und das energiebegrenzte Signal
- $$x_{\varepsilon} (t) = \rm e^{\it -\varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.01cm} t \hspace{0.01cm}\vert}{.}$$
- Hierbei gelte $\varepsilon > 0$. Im Grenzübergang $\varepsilon \to 0$ geht $x_{\varepsilon}(t)$ in $x(t)=1$ über.
- Zur Spektraldarstellung kommt man durch Anwendung des vorne angegebenen Fourierintegrals:
- $$X_\varepsilon (f)=\int_{-\infty}^{0} {\rm e}^{\varepsilon{t} }\, {\cdot}\, {\rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t \hspace{0.2cm}+ \hspace{0.2cm} \int_{0}^{+\infty} {\rm e}^{-\varepsilon t} \,{\cdot}\, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$
- Nach Integration und Zusammenfassen beider Anteile erhalten wir die rein reelle Spektralfunktion des energiebegrenzten Signals $x_{\varepsilon}(t)$:
- $$X_\varepsilon (f)=\frac{1}{\varepsilon -\rm j \cdot 2\pi \it f} + \frac{1}{\varepsilon+\rm j \cdot 2\pi \it f} = \frac{2\varepsilon}{\varepsilon^2 + (\rm 2\pi {\it f}\hspace{0.05cm} ) \rm ^2} \, .$$
- Die Fläche unter der $X_\varepsilon (f)$–Kurve ist unabhängig vom Parameter $\varepsilon$ gleich $1$. Je kleiner $ε$ gewählt wird, um so schmaler und höher wird die Funktion, wie das Lernvideo Herleitung und Visualisierung der Diracfunktion zeigt.
- Der Grenzübergang für $\varepsilon \to 0$ liefert die Diracfunktion mit dem Gewicht $1$:
- $$\lim_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm} 0}X_\varepsilon (f)= \delta(f).$$
Aufgaben zum Kapitel
Aufgabe 2.2: Gleichsignalanteile
Aufgabe 2.2Z: Nichtlinearitäten