Informationstheorie/AWGN–Kanalkapazität bei wertkontinuierlichem Eingang: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (31 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
==Transinformation zwischen wertkontinuierlichen Zufallsgrößen == | ==Transinformation zwischen wertkontinuierlichen Zufallsgrößen == | ||
| + | <br> | ||
| + | Im Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Informationstheoretisches_Modell_der_Digitalsignal.C3.BCbertragung|Informationstheoretisches Modell der Digitalsignalübertragung]] wurde die '''Transinformation''' (englisch: "Mutual Information") zwischen den beiden wertdiskreten Zufallsgrößen $X$ und $Y$ unter anderem in folgender Form angegeben: | ||
| + | |||
| + | :$$I(X;Y) = \hspace{0.5cm} \sum_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\sum_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | ||
| + | \hspace{-0.9cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$ | ||
| − | + | Diese Gleichung entspricht gleichzeitig der [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Relative_Entropie_.E2.80.93_Kullback.E2.80.93Leibler.E2.80.93Distanz|"Kullback–Leibler–Distanz"]] (kurz "KLD") zwischen der Verbundwahrscheinlichkeitsfunktion $P_{XY}$ und dem Produkt der beiden Einzelwahrscheinlichkeitsfunktionen $P_X$ und $P_Y$: | |
| − | + | :$$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$ | |
| + | |||
| + | Um daraus die Transinformation $I(X; Y)$ zwischen zwei wertkontinuierlichen Zufallsgrößen $X$ und $Y$ abzuleiten, geht man wie folgt vor, wobei Hochkommata auf eine quantisierte Größe hinweisen: | ||
| + | *Man quantisiert die Zufallsgrößen $X$ und $Y$ $($mit den Quantisierungsintervallen ${\it Δ}x$ und ${\it Δ}y)$ und erhält so die Wahrscheinlichkeitsfunktionen $P_{X\hspace{0.01cm}′}$ und $P_{Y\hspace{0.01cm}′}$. | ||
| + | *Die „Vektoren” $P_{X\hspace{0.01cm}′}$ und $P_{Y\hspace{0.01cm}′}$ werden nach den Grenzübergängen ${\it Δ}x → 0,\hspace{0.15cm}{\it Δ}y → 0$ unendlich lang, und auch die Verbund–PMF $P_{X\hspace{0.01cm}′\hspace{0.08cm}Y\hspace{0.01cm}′}$ ist dann in der Fläche unendlich weit ausgedehnt. | ||
| + | *Durch diese Grenzübergänge ergeben sich die Wahrscheinlichkeitsdichtefunktionen der kontinuierlichen Zufallsgrößen entsprechend den folgenden Gleichungen: | ||
| − | + | :$$f_X(x_{\mu}) = \frac{P_{X\hspace{0.01cm}'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, | |
| − | + | \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y\hspace{0.01cm}'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, | |
| − | + | \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X\hspace{0.01cm}'\hspace{0.03cm}Y\hspace{0.01cm}'}(x_{\mu}\hspace{0.05cm}, y_{\mu})} {{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$ | |
| − | + | ||
| + | *Aus der Doppelsumme in der obigen Gleichung wird nach der Umbenennung $Δx → {\rm d}x$ bzw. $Δy → {\rm d}y$ die für wertkontinuierliche Zufallsgrößen gültige Gleichung: | ||
| − | + | :$$I(X;Y) = \hspace{0.5cm} \int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | |
| + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } | ||
| + | {f_{X}(x) \cdot f_{Y}(y)} | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Durch Aufspaltung dieses Doppelintegrals lässt sich für die Transinformation auch schreiben: | ||
| − | + | :$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$ | |
| + | |||
| + | Verwendet ist hierbei die »differentielle Verbund–Entropie« | ||
| − | + | :$$h(XY) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | |
| + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big[f_{XY}(x, y) \big] | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$ | ||
| + | |||
| + | sowie die beiden »differentiellen Einzel–Entropien« | ||
| + | |||
| + | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x | ||
| + | \hspace{0.05cm},\hspace{0.5cm} | ||
| + | h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y | ||
| + | \hspace{0.05cm}.$$}} | ||
| + | |||
| + | ==Zur Äquivokation und Irrelevanz== | ||
| + | <br> | ||
| + | Wir gehen weiter von der wertkontinuierlichen Transinformationsgleichung $I(X;Y) = h(X) + h(Y) - h(XY)$ aus. Diese Darstellung findet sich auch im folgenden Schaubild (linke Grafik). | ||
| + | |||
| + | [[Datei:P_ID2882__Inf_T_4_2_S2neu.png|right|frame|Darstellung der Transinformation für wertkontinuierliche Zufallsgrößen]] | ||
| + | |||
| + | Daraus erkennt man, dass die Transinformation auch noch wie folgt dargestellt werden kann: | ||
| − | + | :$$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$ | |
| − | + | ||
| + | Diese fundamentalen informationstheoretischen Zusammenhänge kann man auch aus der rechten Grafik ablesen. Diese gerichtete Darstellung ist für Nachrichtenübertragungssysteme besonders geeignet. | ||
| − | Wir | + | Die abfließende bzw. zufließende differentielle Entropie kennzeichnen |
| + | *die '''Äquivokation''' (englisch: "Equivocation"): | ||
| + | :$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | ||
| + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \big] | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y,$$ | ||
| + | |||
| + | *die '''Irrelevanz''' (englisch: "Irrelevance"): | ||
| + | |||
| + | :$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | ||
| + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \big] | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y.$$ | ||
| + | |||
| + | Auf die Bedeutung dieser beiden informationstheoretischen Größen wird in der [[Aufgaben:4.5Z_Nochmals_Transinformation|Aufgabe 4.5Z]] noch genauer eingegangen. | ||
| + | |||
| + | Vergleicht man die grafischen Darstellungen der Transinformation bei | ||
| + | *wertdiskreten Zufallsgrößen im Abschnitt [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Informationstheoretisches_Modell_der_Digitalsignal.C3.BCbertragung|Informationstheoretisches Modell der Digitalsignalübertragung]] und | ||
| + | *wertkontinuierlichen Zufallsgrößen entsprechend obigem Schaubild, | ||
| + | |||
| + | |||
| + | so erkennt man als einziges Unterscheidungsmerkmal, dass jedes (große) $H$ (Entropie; größer/gleich Null) durch ein (kleines) $h$ (differentielle Entropie; kann positiv, negativ oder Null sein) ersetzt wurde. | ||
| + | *Ansonsten ist die Transinformation in beiden Darstellungen gleich und es gilt stets $I(X; Y) ≥ 0$. | ||
| + | *Im Folgenden verwenden wir meist den „Logarithmus dualis” ⇒ $\log_2$ und erhalten somit die Transinformation in „bit”. | ||
| + | |||
| + | |||
| + | ==Transinformationsberechnung bei additiver Störung == | ||
| + | <br> | ||
| + | Wir betrachten nun ein sehr einfaches Modell der Nachrichtenübertragung: | ||
| + | *Die Zufallsgröße $X$ steht für das (mittelwertfreie) Sendesignal und ist durch die WDF $f_X(x)$ und die Varianz $σ_X^2$ gekennzeichnet. Die Sendeleistung ist $P_X = σ_X^2$. | ||
| + | *Die additive Störung $N$ ist durch die (mittelwertfreie) WDF $f_N(n)$ und die Störleistung $P_N = σ_N^2$ gegeben. | ||
| + | *Wenn $X$ und $N$ als statistisch unabhängig angenommen werden ⇒ signalunabhängiges Rauschen, dann gilt $\text{E}\big[X · N \big] = \text{E}\big[X \big] · \text{E}\big[N\big] = 0$ . | ||
| + | *Das Empfangssignal ist $Y = X + N$. Die Ausgangs–WDF $f_Y(y)$ ist mit der [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Faltung_im_Zeitbereich|Faltungsoperation]] berechenbar ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$. | ||
| + | |||
| + | [[Datei:Inf_T_4_2_S3neu.png|right|frame|Nachrichtenübertragungssystem mit additiver Störung]] | ||
| + | * Für die Empfangsleistung (Varianz) gilt: | ||
| − | + | :$$P_Y = \sigma_Y^2 = {\rm E}\big[Y^2\big] = {\rm E}\big[(X+N)^2\big] = {\rm E}\big[X^2\big] + {\rm E}\big[N^2\big] = \sigma_X^2 + \sigma_N^2 $$ | |
| + | :$$\Rightarrow \hspace{0.3cm} P_Y = P_X + P_N | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die nebenstehend skizzierten Dichtefunktionen (rechteck– bzw. trapezförmig) sollen nur den Rechengang verdeutlichen und haben keine praktische Relevanz. | ||
| + | <br clear=all> | ||
| + | Zur Berechnung der Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ gibt es entsprechend dem [[Informationstheorie/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Zur_.C3.84quivokation_und_Irrelevanz|Schaubild auf der vorherigen Seite]] drei Möglichkeiten: | ||
| + | * Berechnung entsprechend $I(X, Y) = h(X) + h(Y) - h(XY)$: | ||
| + | :Die beiden ersten Terme sind aus $f_X(x)$ bzw. $f_Y(y)$ in einfacher Weise berechenbar. Problematisch ist die »differentielle Verbundentropie« $h(XY)$. Hierzu benötigt man die 2D–Verbund–WDF $f_{XY}(x, y)$, die meist nicht direkt gegeben ist. | ||
| + | |||
| + | * Berechnung entsprechend $I(X, Y) = h(Y) - h(Y|X)$: | ||
| + | :Hierbei bezeichnet $h(Y|X)$ die »differentielle Streuentropie«. Es gilt $h(Y|X) = h(X + N|X) = h(N)$, so dass $I(X; Y)$ bei Kenntnis von $f_X(x)$ und $f_N(n)$ über die Gleichung $f_Y(y) = f_X(x) ∗ f_N(n)$ sehr einfach zu berechnen ist. | ||
| + | |||
| + | * Berechnung entsprechend $I(X, Y) = h(X) - h(X|Y)$: | ||
| + | :Nach dieser Gleichung benötigt man allerdings die » differentielle Rückschlussentropie« $h(X|Y)$, die schwieriger angebbar ist als $h(Y|X)$. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Im Folgenden verwenden wir die mittlere Gleichung und schreiben für die Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ eines Nachrichtenübertragungssystems bei additiver und unkorrelierter Störung $N$: | ||
| + | |||
| + | :$$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} | ||
| + | -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y | ||
| + | +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} \big[f_N(n)\big] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$}} | ||
| − | |||
| − | + | ==Kanalkapazität des AWGN–Kanals== | |
| − | *die | + | <br> |
| + | Spezifiziert man im bisherigen [[Informationstheorie/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Transinformationsberechnung_bei_additiver_St.C3.B6rung|allgemeinen Systemmodell]] die Wahrscheinlichkeitsdichtefunktion der Störung (bzw. des Rauschens) als gaußisch entsprechend | ||
| + | [[Datei:P_ID2884__Inf_T_4_2_S4_neu.png|right|frame|Zur Herleitung der AWGN–Kanalkapazität]] | ||
| + | :$$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm e}^{ | ||
| + | - \hspace{0.05cm}{n^2}/(2 \sigma_N^2) } \hspace{0.05cm}, $$ | ||
| + | |||
| + | so erhalten wir das rechts skizzierte Modell zur Berechnung der Kanalkapazität des so genannten [[Modulationsverfahren/Qualitätskriterien#Einige_Anmerkungen_zum_AWGN.E2.80.93Kanalmodell|AWGN–Kanals]] ("Additive White Gaussian Noise"). Meist ersetzen wir im Folgenden die Varianz $\sigma_N^2$ durch die Leistung $P_N$. | ||
| + | <br clear=all> | ||
| + | Aus vorherigen Abschnitten wissen wir: | ||
| + | *Die [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Definition_und_Bedeutung_der_Kanalkapazit.C3.A4t|Kanalkapazität]] $C_{\rm AWGN}$ gibt die maximale Transinformation $I(X; Y)$ zwischen der Eingangsgröße $X$ und der Ausgangsgröße $Y$ des AWGN–Kanals an. Die Maximierung bezieht sich dabei auf die bestmögliche Eingangs–WDF. Somit gilt unter der Nebenbedingung der [[Informationstheorie/Differentielle_Entropie#Differentielle_Entropie_einiger_leistungsbegrenzter_Zufallsgr.C3.B6.C3.9Fen|Leistungsbegrenzung]]: | ||
| − | + | :$$C_{\rm AWGN} = \max_{f_X:\hspace{0.1cm} {\rm E}[X^2 ] \le P_X} \hspace{-0.35cm} I(X;Y) | |
| − | + | = -h(N) + \max_{f_X:\hspace{0.1cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) | |
| − | + | \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | + | :Es ist bereits berücksichtigt, dass sich die Maximierung allein auf die differentielle Entropie $h(Y)$ ⇒ Wahrscheinlichkeitsdichtefunktion $f_Y(y)$ bezieht. Bei gegebener Störleistung $P_N$ ist nämlich $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ eine Konstante. | |
| − | + | *Das Maximum für $h(Y)$ erhält man für eine Gaußsche WDF $f_Y(y)$ mit $P_Y = P_X + P_N$ t, siehe [[Informationstheorie/Differentielle_Entropie#Beweis:_Maximale_differentielle_Entropie_bei_Leistungsbegrenzung|Maximale differentielle Entropie bei Leistungsbegrenzung]]: | |
| + | :$${\rm max}\big[h(Y)\big] = 1/2 · \log_2 \big[2πe · (P_X + P_N)\big].$$ | ||
| + | *Die Ausgangs–WDF $f_Y(y) = f_X(x) ∗ f_N(n)$ ist aber nur dann gaußförmig, wenn sowohl $f_X(x)$ als auch $f_N(n)$ Gaußfunktionen sind. Ein plakativer Merkspruch zur Faltungsoperation lautet nämlich: '''Gauß bleibt Gauß, und Nicht–Gauß wird nie (exakt) Gauß'''. | ||
| − | = | + | [[Datei:P_ID2885__Inf_T_4_2_S4b_neu.png|right|frame|Numerische Ergebnisse für die AWGN–Kanalkapazität als Funktion von ${P_X}/{P_N}$]] |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Beim AWGN–Kanal ⇒ Gaußsche Rausch-WDF $f_N(n)$ ergibt sich die '''Kanalkapazität''' genau dann, wenn die Eingangs–WDF $f_X(x)$ ebenfalls gaußförmig ist: | ||
| − | + | :$$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} {P_Y}/{P_N}$$ | |
| − | + | :$$\Rightarrow \hspace{0.3cm} C_{\rm AWGN}= 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + P_X/P_N) \hspace{0.05cm}.$$}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Parallele Gaußsche Kanäle == | ==Parallele Gaußsche Kanäle == | ||
| − | == | + | <br> |
| + | [[Datei:P_ID2891__Inf_T_4_2_S4c_neu.png|frame|Parallele AWGN–Kanäle]] | ||
| + | |||
| + | Wir betrachten nun entsprechend der Grafik $K$ parallele Gaußkanäle von $X_1 → Y_1$, ... , $X_k → Y_k$, ... , $X_K → Y_K$. | ||
| + | *Die Sendeleistungen in den $K$ Kanälen nennen wir | ||
| + | :$$P_1 = \text{E}[X_1^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_k = \text{E}[X_k^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_K = \text{E}[X_K^2].$$ | ||
| + | *Die $K$ Störleistungen können ebenfalls unterschiedlich sein: | ||
| + | :$$σ_1^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_k^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_K^2.$$ | ||
| + | |||
| + | |||
| + | Gesucht ist nun die maximale Transinformation $I(X_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, Y_K) $ zwischen | ||
| + | *den $K$ Eingangsgrößen $X_1$, ... , $X_K$ sowie | ||
| + | *den $K$ Ausgangsgrößen $Y_1$ , ... , $Y_K$, | ||
| + | |||
| + | |||
| + | die wir als die '''Gesamt–Kanalkapazität''' dieser AWGN–Konfiguration bezeichnen. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Vereinbarung:}$ | ||
| + | Ausgegangen wird von Leistungsbegrenzung des Gesamtsystems. Das heißt: <br> Die Summe aller Leistungen $P_k$ in den $K$ Einzelkanälen darf den vorgegebenen Wert $P_X$ nicht überschreiten: | ||
| + | |||
| + | :$$P_1 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K | ||
| + | \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | Unter der nur wenig einschränkenden Annahme unabhängiger Störquellen $N_1$, ... , $N_K$ kann für die Transinformation nach einigen Zwischenschritten geschrieben werden: | ||
| + | |||
| + | :$$I(X_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K | ||
| + | \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Dafür ist folgende obere Schranke angebbar: | ||
| + | |||
| + | :$$I(X_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, Y_K) | ||
| + | \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} \big[h(Y_k) - h(N_k)\big] | ||
| + | \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + {P_k}/{\sigma_k^2}) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Das Gleichheitszeichen (Identität) gilt bei mittelwertfreien Gaußschen Eingangsgrößen $X_k$ sowie bei statistisch voneinander unabhängigen Störungen $N_k$. | ||
| + | *Man kommt von dieser Gleichung zur "maximalen Transinformation" ⇒ "Kanalkapazität", wenn man die gesamte Sendeleistung $P_X$ unter Berücksichtigung der unterschiedlichen Störungen in den einzelnen Kanälen $(σ_k^2)$ bestmöglich aufteilt. | ||
| + | *Dieses Optimierungsproblem lässt sich wieder mit dem Verfahren der [https://de.wikipedia.org/wiki/Lagrange-Multiplikator Lagrange–Multiplikatoren] elegant lösen. Das folgende Beispiel erläutert nur das Ergebnis. | ||
| + | |||
| + | |||
| + | [[Datei:P_ID2894__Inf_T_4_2_S4d.png|right|frame|Bestmögliche Leistungsaufteilung für $K = 4$ („Water–Filling”)]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Wir betrachten $K = 4$ parallele Gaußkanäle mit vier unterschiedlichen Störleistungen $σ_1^2$, ... , $σ_4^2$ gemäß der nebenstehenden Abbildung (schwach–grüne Hinterlegung). | ||
| + | *Gesucht ist die bestmögliche Aufteilung der Sendeleistung auf die vier Kanäle. | ||
| + | *Würde man dieses Profil langsam mit Wasser auffüllen, so würde das Wasser zunächst nur in den $\text{Kanal 2}$ fließen. | ||
| + | *Gießt man weiter, so sammelt sich auch im $\text{Kanal 1}$ etwas Wasser an und später auch im $\text{Kanal 4}$. | ||
| + | |||
| + | |||
| + | Die eingezeichnete „Wasserhöhe” $H$ beschreibt genau den Zeitpunkt, zu dem die Summe $P_1 + P_2 + P_4$ der insgesamt zur Verfügung stehenden Sendeleistung $P_X$ entspricht: | ||
| + | *Die optimale Leistungsaufteilung für dieses Beispiel ergibt $P_2 > P_1 > P_4$ sowie $P_3 = 0$. | ||
| + | *Erst bei größerer Sendeleistung $P_X$ würde auch dem dritten Kanal eine kleine Leistung $P_3$ zugewiesen. | ||
| + | |||
| + | |||
| + | Man bezeichnet dieses Allokationsverfahren als '''Water–Filling–Algorithmus'''.}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
| + | Werden alle $K$ Gaußkanäle in gleicher Weise gestört ⇒ $σ_1^2 = \hspace{0.15cm}\text{...}\hspace{0.15cm} = σ_K^2 = P_N$, so sollte man natürlich die gesamte zur Verfügung stehende Sendeleistung $P_X$ gleichmäßig auf alle Kanäle verteilen: $P_k = P_X/K$. Für die Gesamtkapazität erhält man dann: | ||
| + | [[Datei:P_ID2939__Inf_T_4_2_S5_neu.png|right|frame|Kapazität für $K$ parallele Kanäle]] | ||
| + | :$$C_{\rm Gesamt} | ||
| + | = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Grafik zeigt die Gesamtkapazität als Funktion von $P_X/P_N$ für $K = 1$, $K = 2$ und $K = 3$: | ||
| + | *Bei $P_X/P_N = 10 \ ⇒ \ 10 · \text{lg} (P_X/P_N) = 10 \ \text{dB}$ wird die Gesamtkapazität um ca. $50\%$ größer, wenn man die Gesamtleistung $P_X$ auf zwei Kanäle gleichmäßig aufteilt: $P_1 = P_2 = P_X/2$. | ||
| + | *Im Grenzfall $P_X/P_N → ∞$ nimmt die Gesamtkapazität um den Faktor $K$ zu ⇒ Verdoppelung bei $K = 2$. | ||
| + | |||
| + | |||
| + | Die beiden identischen und voneinander unabhängigen Kanäle kann man auf unterschiedliche Weise realisieren, zum Beispiel durch Multiplexverfahren in Zeit, Frequenz oder Raum. | ||
| + | |||
| + | Der Fall $K = 2$ lässt sich aber auch durch die Verwendung orthogonaler Basisfunktionen wie „Cosinus” und „Sinus” verwirklichen wie zum Beispiel bei | ||
| + | *der [[Modulationsverfahren/Quadratur–Amplitudenmodulation|Quadratur–Amplitudenmodulation]] (QAM) oder | ||
| + | *einer [[Modulationsverfahren/Quadratur–Amplitudenmodulation#Weitere_Signalraumkonstellationen|mehrstufigen Phasenmodulation]] wie QPSK oder 8–PSK.}} | ||
| + | |||
| + | ==Aufgaben zum Kapitel == | ||
| + | <br> | ||
| + | [[Aufgaben:4.5 Transinformation aus 2D-WDF|Aufgabe 4.5: Transinformation aus 2D-WDF]] | ||
| + | |||
| + | [[Aufgaben:4.5Z Nochmals Transinformation|Aufgabe 4.5Z: Nochmals Transinformation]] | ||
| + | |||
| + | [[Aufgaben:4.6 AWGN–Kanalkapazität|Aufgabe 4.6: AWGN–Kanalkapazität]] | ||
| + | |||
| + | [[Aufgaben:4.7 Mehrere parallele Gaußkanäle|Aufgabe 4.7: Mehrere parallele Gaußkanäle]] | ||
| + | [[Aufgaben:4.7Z Zum Water–Filling–Algorithmus|Aufgabe 4.7Z: Zum Water–Filling–Algorithmus]] | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 20. August 2021, 15:16 Uhr
Inhaltsverzeichnis
Transinformation zwischen wertkontinuierlichen Zufallsgrößen
Im Kapitel Informationstheoretisches Modell der Digitalsignalübertragung wurde die Transinformation (englisch: "Mutual Information") zwischen den beiden wertdiskreten Zufallsgrößen $X$ und $Y$ unter anderem in folgender Form angegeben:
- $$I(X;Y) = \hspace{0.5cm} \sum_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\sum_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$
Diese Gleichung entspricht gleichzeitig der "Kullback–Leibler–Distanz" (kurz "KLD") zwischen der Verbundwahrscheinlichkeitsfunktion $P_{XY}$ und dem Produkt der beiden Einzelwahrscheinlichkeitsfunktionen $P_X$ und $P_Y$:
- $$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$
Um daraus die Transinformation $I(X; Y)$ zwischen zwei wertkontinuierlichen Zufallsgrößen $X$ und $Y$ abzuleiten, geht man wie folgt vor, wobei Hochkommata auf eine quantisierte Größe hinweisen:
- Man quantisiert die Zufallsgrößen $X$ und $Y$ $($mit den Quantisierungsintervallen ${\it Δ}x$ und ${\it Δ}y)$ und erhält so die Wahrscheinlichkeitsfunktionen $P_{X\hspace{0.01cm}′}$ und $P_{Y\hspace{0.01cm}′}$.
- Die „Vektoren” $P_{X\hspace{0.01cm}′}$ und $P_{Y\hspace{0.01cm}′}$ werden nach den Grenzübergängen ${\it Δ}x → 0,\hspace{0.15cm}{\it Δ}y → 0$ unendlich lang, und auch die Verbund–PMF $P_{X\hspace{0.01cm}′\hspace{0.08cm}Y\hspace{0.01cm}′}$ ist dann in der Fläche unendlich weit ausgedehnt.
- Durch diese Grenzübergänge ergeben sich die Wahrscheinlichkeitsdichtefunktionen der kontinuierlichen Zufallsgrößen entsprechend den folgenden Gleichungen:
- $$f_X(x_{\mu}) = \frac{P_{X\hspace{0.01cm}'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y\hspace{0.01cm}'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X\hspace{0.01cm}'\hspace{0.03cm}Y\hspace{0.01cm}'}(x_{\mu}\hspace{0.05cm}, y_{\mu})} {{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$
- Aus der Doppelsumme in der obigen Gleichung wird nach der Umbenennung $Δx → {\rm d}x$ bzw. $Δy → {\rm d}y$ die für wertkontinuierliche Zufallsgrößen gültige Gleichung:
- $$I(X;Y) = \hspace{0.5cm} \int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } {f_{X}(x) \cdot f_{Y}(y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$
$\text{Fazit:}$ Durch Aufspaltung dieses Doppelintegrals lässt sich für die Transinformation auch schreiben:
- $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$
Verwendet ist hierbei die »differentielle Verbund–Entropie«
- $$h(XY) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big[f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$
sowie die beiden »differentiellen Einzel–Entropien«
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},\hspace{0.5cm} h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
Zur Äquivokation und Irrelevanz
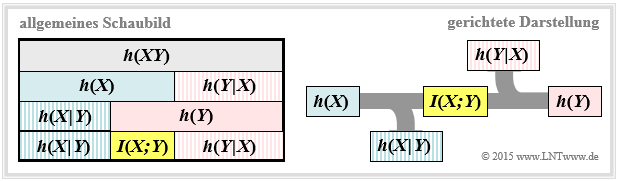
Wir gehen weiter von der wertkontinuierlichen Transinformationsgleichung $I(X;Y) = h(X) + h(Y) - h(XY)$ aus. Diese Darstellung findet sich auch im folgenden Schaubild (linke Grafik).
Daraus erkennt man, dass die Transinformation auch noch wie folgt dargestellt werden kann:
- $$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$
Diese fundamentalen informationstheoretischen Zusammenhänge kann man auch aus der rechten Grafik ablesen. Diese gerichtete Darstellung ist für Nachrichtenübertragungssysteme besonders geeignet.
Die abfließende bzw. zufließende differentielle Entropie kennzeichnen
- die Äquivokation (englisch: "Equivocation"):
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y,$$
- die Irrelevanz (englisch: "Irrelevance"):
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y.$$
Auf die Bedeutung dieser beiden informationstheoretischen Größen wird in der Aufgabe 4.5Z noch genauer eingegangen.
Vergleicht man die grafischen Darstellungen der Transinformation bei
- wertdiskreten Zufallsgrößen im Abschnitt Informationstheoretisches Modell der Digitalsignalübertragung und
- wertkontinuierlichen Zufallsgrößen entsprechend obigem Schaubild,
so erkennt man als einziges Unterscheidungsmerkmal, dass jedes (große) $H$ (Entropie; größer/gleich Null) durch ein (kleines) $h$ (differentielle Entropie; kann positiv, negativ oder Null sein) ersetzt wurde.
- Ansonsten ist die Transinformation in beiden Darstellungen gleich und es gilt stets $I(X; Y) ≥ 0$.
- Im Folgenden verwenden wir meist den „Logarithmus dualis” ⇒ $\log_2$ und erhalten somit die Transinformation in „bit”.
Transinformationsberechnung bei additiver Störung
Wir betrachten nun ein sehr einfaches Modell der Nachrichtenübertragung:
- Die Zufallsgröße $X$ steht für das (mittelwertfreie) Sendesignal und ist durch die WDF $f_X(x)$ und die Varianz $σ_X^2$ gekennzeichnet. Die Sendeleistung ist $P_X = σ_X^2$.
- Die additive Störung $N$ ist durch die (mittelwertfreie) WDF $f_N(n)$ und die Störleistung $P_N = σ_N^2$ gegeben.
- Wenn $X$ und $N$ als statistisch unabhängig angenommen werden ⇒ signalunabhängiges Rauschen, dann gilt $\text{E}\big[X · N \big] = \text{E}\big[X \big] · \text{E}\big[N\big] = 0$ .
- Das Empfangssignal ist $Y = X + N$. Die Ausgangs–WDF $f_Y(y)$ ist mit der Faltungsoperation berechenbar ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$.
- Für die Empfangsleistung (Varianz) gilt:
- $$P_Y = \sigma_Y^2 = {\rm E}\big[Y^2\big] = {\rm E}\big[(X+N)^2\big] = {\rm E}\big[X^2\big] + {\rm E}\big[N^2\big] = \sigma_X^2 + \sigma_N^2 $$
- $$\Rightarrow \hspace{0.3cm} P_Y = P_X + P_N \hspace{0.05cm}.$$
Die nebenstehend skizzierten Dichtefunktionen (rechteck– bzw. trapezförmig) sollen nur den Rechengang verdeutlichen und haben keine praktische Relevanz.
Zur Berechnung der Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ gibt es entsprechend dem Schaubild auf der vorherigen Seite drei Möglichkeiten:
- Berechnung entsprechend $I(X, Y) = h(X) + h(Y) - h(XY)$:
- Die beiden ersten Terme sind aus $f_X(x)$ bzw. $f_Y(y)$ in einfacher Weise berechenbar. Problematisch ist die »differentielle Verbundentropie« $h(XY)$. Hierzu benötigt man die 2D–Verbund–WDF $f_{XY}(x, y)$, die meist nicht direkt gegeben ist.
- Berechnung entsprechend $I(X, Y) = h(Y) - h(Y|X)$:
- Hierbei bezeichnet $h(Y|X)$ die »differentielle Streuentropie«. Es gilt $h(Y|X) = h(X + N|X) = h(N)$, so dass $I(X; Y)$ bei Kenntnis von $f_X(x)$ und $f_N(n)$ über die Gleichung $f_Y(y) = f_X(x) ∗ f_N(n)$ sehr einfach zu berechnen ist.
- Berechnung entsprechend $I(X, Y) = h(X) - h(X|Y)$:
- Nach dieser Gleichung benötigt man allerdings die » differentielle Rückschlussentropie« $h(X|Y)$, die schwieriger angebbar ist als $h(Y|X)$.
$\text{Fazit:}$ Im Folgenden verwenden wir die mittlere Gleichung und schreiben für die Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ eines Nachrichtenübertragungssystems bei additiver und unkorrelierter Störung $N$:
- $$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} \big[f_N(n)\big] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$
Kanalkapazität des AWGN–Kanals
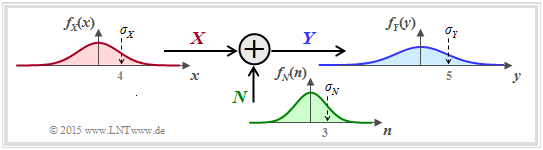
Spezifiziert man im bisherigen allgemeinen Systemmodell die Wahrscheinlichkeitsdichtefunktion der Störung (bzw. des Rauschens) als gaußisch entsprechend
- $$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}/(2 \sigma_N^2) } \hspace{0.05cm}, $$
so erhalten wir das rechts skizzierte Modell zur Berechnung der Kanalkapazität des so genannten AWGN–Kanals ("Additive White Gaussian Noise"). Meist ersetzen wir im Folgenden die Varianz $\sigma_N^2$ durch die Leistung $P_N$.
Aus vorherigen Abschnitten wissen wir:
- Die Kanalkapazität $C_{\rm AWGN}$ gibt die maximale Transinformation $I(X; Y)$ zwischen der Eingangsgröße $X$ und der Ausgangsgröße $Y$ des AWGN–Kanals an. Die Maximierung bezieht sich dabei auf die bestmögliche Eingangs–WDF. Somit gilt unter der Nebenbedingung der Leistungsbegrenzung:
- $$C_{\rm AWGN} = \max_{f_X:\hspace{0.1cm} {\rm E}[X^2 ] \le P_X} \hspace{-0.35cm} I(X;Y) = -h(N) + \max_{f_X:\hspace{0.1cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) \hspace{0.05cm}.$$
- Es ist bereits berücksichtigt, dass sich die Maximierung allein auf die differentielle Entropie $h(Y)$ ⇒ Wahrscheinlichkeitsdichtefunktion $f_Y(y)$ bezieht. Bei gegebener Störleistung $P_N$ ist nämlich $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ eine Konstante.
- Das Maximum für $h(Y)$ erhält man für eine Gaußsche WDF $f_Y(y)$ mit $P_Y = P_X + P_N$ t, siehe Maximale differentielle Entropie bei Leistungsbegrenzung:
- $${\rm max}\big[h(Y)\big] = 1/2 · \log_2 \big[2πe · (P_X + P_N)\big].$$
- Die Ausgangs–WDF $f_Y(y) = f_X(x) ∗ f_N(n)$ ist aber nur dann gaußförmig, wenn sowohl $f_X(x)$ als auch $f_N(n)$ Gaußfunktionen sind. Ein plakativer Merkspruch zur Faltungsoperation lautet nämlich: Gauß bleibt Gauß, und Nicht–Gauß wird nie (exakt) Gauß.
$\text{Fazit:}$ Beim AWGN–Kanal ⇒ Gaußsche Rausch-WDF $f_N(n)$ ergibt sich die Kanalkapazität genau dann, wenn die Eingangs–WDF $f_X(x)$ ebenfalls gaußförmig ist:
- $$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} {P_Y}/{P_N}$$
- $$\Rightarrow \hspace{0.3cm} C_{\rm AWGN}= 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + P_X/P_N) \hspace{0.05cm}.$$
Parallele Gaußsche Kanäle
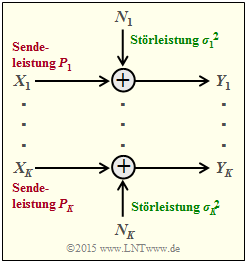
Wir betrachten nun entsprechend der Grafik $K$ parallele Gaußkanäle von $X_1 → Y_1$, ... , $X_k → Y_k$, ... , $X_K → Y_K$.
- Die Sendeleistungen in den $K$ Kanälen nennen wir
- $$P_1 = \text{E}[X_1^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_k = \text{E}[X_k^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_K = \text{E}[X_K^2].$$
- Die $K$ Störleistungen können ebenfalls unterschiedlich sein:
- $$σ_1^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_k^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_K^2.$$
Gesucht ist nun die maximale Transinformation $I(X_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, Y_K) $ zwischen
- den $K$ Eingangsgrößen $X_1$, ... , $X_K$ sowie
- den $K$ Ausgangsgrößen $Y_1$ , ... , $Y_K$,
die wir als die Gesamt–Kanalkapazität dieser AWGN–Konfiguration bezeichnen.
$\text{Vereinbarung:}$
Ausgegangen wird von Leistungsbegrenzung des Gesamtsystems. Das heißt:
Die Summe aller Leistungen $P_k$ in den $K$ Einzelkanälen darf den vorgegebenen Wert $P_X$ nicht überschreiten:
- $$P_1 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$
Unter der nur wenig einschränkenden Annahme unabhängiger Störquellen $N_1$, ... , $N_K$ kann für die Transinformation nach einigen Zwischenschritten geschrieben werden:
- $$I(X_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$
Dafür ist folgende obere Schranke angebbar:
- $$I(X_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, Y_K) \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} \big[h(Y_k) - h(N_k)\big] \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + {P_k}/{\sigma_k^2}) \hspace{0.05cm}.$$
- Das Gleichheitszeichen (Identität) gilt bei mittelwertfreien Gaußschen Eingangsgrößen $X_k$ sowie bei statistisch voneinander unabhängigen Störungen $N_k$.
- Man kommt von dieser Gleichung zur "maximalen Transinformation" ⇒ "Kanalkapazität", wenn man die gesamte Sendeleistung $P_X$ unter Berücksichtigung der unterschiedlichen Störungen in den einzelnen Kanälen $(σ_k^2)$ bestmöglich aufteilt.
- Dieses Optimierungsproblem lässt sich wieder mit dem Verfahren der Lagrange–Multiplikatoren elegant lösen. Das folgende Beispiel erläutert nur das Ergebnis.
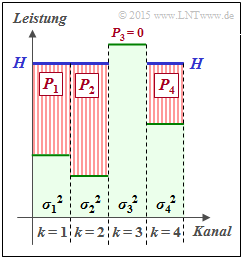
$\text{Beispiel 1:}$ Wir betrachten $K = 4$ parallele Gaußkanäle mit vier unterschiedlichen Störleistungen $σ_1^2$, ... , $σ_4^2$ gemäß der nebenstehenden Abbildung (schwach–grüne Hinterlegung).
- Gesucht ist die bestmögliche Aufteilung der Sendeleistung auf die vier Kanäle.
- Würde man dieses Profil langsam mit Wasser auffüllen, so würde das Wasser zunächst nur in den $\text{Kanal 2}$ fließen.
- Gießt man weiter, so sammelt sich auch im $\text{Kanal 1}$ etwas Wasser an und später auch im $\text{Kanal 4}$.
Die eingezeichnete „Wasserhöhe” $H$ beschreibt genau den Zeitpunkt, zu dem die Summe $P_1 + P_2 + P_4$ der insgesamt zur Verfügung stehenden Sendeleistung $P_X$ entspricht:
- Die optimale Leistungsaufteilung für dieses Beispiel ergibt $P_2 > P_1 > P_4$ sowie $P_3 = 0$.
- Erst bei größerer Sendeleistung $P_X$ würde auch dem dritten Kanal eine kleine Leistung $P_3$ zugewiesen.
Man bezeichnet dieses Allokationsverfahren als Water–Filling–Algorithmus.
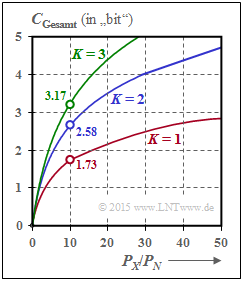
$\text{Beispiel 2:}$ Werden alle $K$ Gaußkanäle in gleicher Weise gestört ⇒ $σ_1^2 = \hspace{0.15cm}\text{...}\hspace{0.15cm} = σ_K^2 = P_N$, so sollte man natürlich die gesamte zur Verfügung stehende Sendeleistung $P_X$ gleichmäßig auf alle Kanäle verteilen: $P_k = P_X/K$. Für die Gesamtkapazität erhält man dann:
- $$C_{\rm Gesamt} = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) \hspace{0.05cm}.$$
Die Grafik zeigt die Gesamtkapazität als Funktion von $P_X/P_N$ für $K = 1$, $K = 2$ und $K = 3$:
- Bei $P_X/P_N = 10 \ ⇒ \ 10 · \text{lg} (P_X/P_N) = 10 \ \text{dB}$ wird die Gesamtkapazität um ca. $50\%$ größer, wenn man die Gesamtleistung $P_X$ auf zwei Kanäle gleichmäßig aufteilt: $P_1 = P_2 = P_X/2$.
- Im Grenzfall $P_X/P_N → ∞$ nimmt die Gesamtkapazität um den Faktor $K$ zu ⇒ Verdoppelung bei $K = 2$.
Die beiden identischen und voneinander unabhängigen Kanäle kann man auf unterschiedliche Weise realisieren, zum Beispiel durch Multiplexverfahren in Zeit, Frequenz oder Raum.
Der Fall $K = 2$ lässt sich aber auch durch die Verwendung orthogonaler Basisfunktionen wie „Cosinus” und „Sinus” verwirklichen wie zum Beispiel bei
- der Quadratur–Amplitudenmodulation (QAM) oder
- einer mehrstufigen Phasenmodulation wie QPSK oder 8–PSK.
Aufgaben zum Kapitel
Aufgabe 4.5: Transinformation aus 2D-WDF
Aufgabe 4.5Z: Nochmals Transinformation
Aufgabe 4.6: AWGN–Kanalkapazität
Aufgabe 4.7: Mehrere parallele Gaußkanäle
Aufgabe 4.7Z: Zum Water–Filling–Algorithmus