Aufgaben:Aufgabe 4.4: Herkömmliche Entropie und differenzielle Entropie: Unterschied zwischen den Versionen
| Zeile 96: | Zeile 96: | ||
:$$H(Z_{X,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X) = | :$$H(Z_{X,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X) = | ||
3\,{\rm bit} +(- 1\,{\rm bit})\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}. $$ | 3\,{\rm bit} +(- 1\,{\rm bit})\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}. $$ | ||
| − | < | + | <u>Hinweis:</u> Nur bei der Gleichverteilung liefert die Näherung genau das gleiche Ergebnis wie die direkte Berechnung, also die tatsächliche Entropie. |
[[Datei:P_ID2880__Inf_A_4_4d.png|right|frame|Quantisierte Zufallsgröße $Z_{Y, \ M = 4}$]] | [[Datei:P_ID2880__Inf_A_4_4d.png|right|frame|Quantisierte Zufallsgröße $Z_{Y, \ M = 4}$]] | ||
| Zeile 109: | Zeile 109: | ||
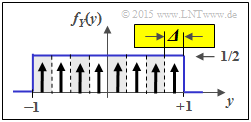
[[Datei:P_ID2881__Inf_A_4_4e.png|right|frame|Quantisierte Zufallsgröße $Z_{Y, \ M = 8}$]] | [[Datei:P_ID2881__Inf_A_4_4e.png|right|frame|Quantisierte Zufallsgröße $Z_{Y, \ M = 8}$]] | ||
| − | '''(5)''' Im Gegensatz zur Teilaufgabe '''( | + | '''(5)''' Im Gegensatz zur Teilaufgabe '''(4)''' gilt nun ${\it \Delta} = 1/4$. Daraus folgt für die „Näherung”: |
:$$H(Z_{Y,\hspace{0.05cm} M = 8}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = | :$$H(Z_{Y,\hspace{0.05cm} M = 8}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = | ||
2\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 3\,{\rm bit}}\hspace{0.05cm}.$$ | 2\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 3\,{\rm bit}}\hspace{0.05cm}.$$ | ||
Man erhält wieder das gleiche Ergebnis wie bei der direkten Berechnung. | Man erhält wieder das gleiche Ergebnis wie bei der direkten Berechnung. | ||
| − | + | ||
| + | |||
'''(6)''' Richtig ist nur die <u>Aussage 1</u>: | '''(6)''' Richtig ist nur die <u>Aussage 1</u>: | ||
* Die Entropie $H(Z)$ einer diskreten Zufallsgröße $Z = \{z_1, \ \text{...} \ , z_M\}$ ist nie negativ. | * Die Entropie $H(Z)$ einer diskreten Zufallsgröße $Z = \{z_1, \ \text{...} \ , z_M\}$ ist nie negativ. | ||
Aktuelle Version vom 28. September 2021, 14:16 Uhr
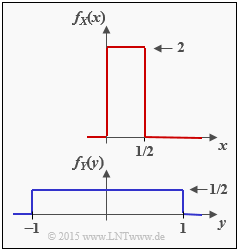
Wir betrachten die beiden wertkontinuierlichen Zufallsgrößen $X$ und $Y$ mit den Wahrscheinlichkeitsdichtefunktionen $f_X(x)$ und $f_Y(y)$. Für diese Zufallsgrößen kann man
- die herkömmlichen Entropien $H(X)$ bzw. $H(Y)$ nicht angeben,
- jedoch aber die differentiellen Entropien $h(X)$ und $h(Y)$.
Wir betrachten außerdem zwei wertdiskrete Zufallsgrößen:
- Die Zufallsgröße $Z_{X,\hspace{0.05cm}M}$ ergibt sich durch (geeignete) Quantisierung der Zufallsgröße $X$ mit der Quantisierungsstufenzahl $M$
⇒ Quantisierungsintervallbreite ${\it \Delta} = 0.5/M$. - Die Zufallsgröße $Z_{Y,\hspace{0.05cm}M}$ ergibt sich nach Quantisierung der Zufallsgröße $Y$ mit der Quantisierungsstufenzahl $M$
⇒ Quantisierungsintervallbreite ${\it \Delta} = 2/M$.
Die Wahrscheinlichkeitsdichtefunktionen dieser diskreten Zufallsgrößen setzen sich jeweils aus $M$ Diracfunktionen zusammen, deren Impulsgewichte durch die Intervallflächen der zugehörigen wertkontinuierlichen Zufallsgrößen gegeben sind.
Daraus lassen sich die Entropien $H(Z_{X,\hspace{0.05cm}M})$ und $H(Z_{Y,\hspace{0.05cm}M})$ in herkömmlicher Weise entsprechend dem Kapitel Wahrscheinlichkeitsfunktion und Entropie bestimmen.
Im Abschnitt Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung wurde auch eine Näherung angegeben. Beispielsweise gilt:
- $$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$
- Im Laufe der Aufgabe wird sich zeigen, dass bei rechteckförmiger WDF ⇒ Gleichverteilung diese „Näherung” das gleiche Ergebnis liefert wie die direkte Berechnung.
- Aber im allgemeinen Fall – so im $\text{Beispiel 2}$ mit dreieckförmiger WDF – stellt obige Gleichung tatsächlich nur eine Näherung dar, die erst im Grenzfall ${\it \Delta} \to 0$ mit der tatsächlichen Entropie $H(Z_{X,\hspace{0.05cm}M})$ übereinstimmt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Nützliche Hinweise zur Lösung dieser Aufgabe finden Sie insbesondere auf der Seite Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung .
Fragebogen
Musterlösung
- $$h(X) = {\rm log}_2 \hspace{0.1cm} (x_{\rm max} - x_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= - 1\,{\rm bit}}\hspace{0.05cm}.$$
(2) Mit $y_{\rm min} = -1$ und $y_{\rm max} = +1$ ergibt sich dagegen für die differentielle Entropie der Zufallsgröße $Y$:
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (y_{\rm max} - y_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= + 1\,{\rm bit}}\hspace{0.05cm}. $$
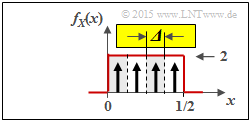
(3) Die nebenstehende Grafik verdeutlicht die bestmögliche Quantisierung der Zufallsgröße $X$ mit der Quantisierungsstufenzahl $M = 4$ ⇒ Zufallsgröße $Z_{X, \ M = 4}$:
- Die Intervallbreite ist hier gleich ${\it \Delta} = 0.5/4 = 1/8$.
- Die möglichen Werte (jeweils in der Intervallmitte) sind $z \in \{0.0625,\ 0.1875,\ 0.3125,\ 0.4375\}$.
Die direkte Entropieberechnung ergibt mit der Wahrscheinlichkeitsfunktion $P_Z(Z) = \big [1/4,\ \text{...} , \ 1/4 \big]$:
- $$H(Z_{X, \ M = 4}) = {\rm log}_2 \hspace{0.1cm} (4) \hspace{0.15cm}\underline{= 2\,{\rm bit}} \hspace{0.05cm}.$$
Mit der Näherung erhält man unter Berücksichtigung des Ergebnisses von (1):
- $$H(Z_{X,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X) = 3\,{\rm bit} +(- 1\,{\rm bit})\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}. $$
Hinweis: Nur bei der Gleichverteilung liefert die Näherung genau das gleiche Ergebnis wie die direkte Berechnung, also die tatsächliche Entropie.
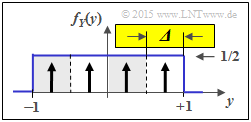
(4) Aus der zweiten Grafik erkennt man die Gemeinsamkeiten / Unterschiede zur Teilaufgabe (3):
- Der Quantisierungsparameter ist nun ${\it \Delta} = 2/4 = 1/2$.
- Die möglichen Werte sind nun $z \in \{\pm 0.75,\ \pm 0.25\}$.
- Somit liefert hier die „Näherung” (ebenso wie die direkte Berechnung) das Ergebnis:
- $$H(Z_{Y,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = 1\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}.$$
(5) Im Gegensatz zur Teilaufgabe (4) gilt nun ${\it \Delta} = 1/4$. Daraus folgt für die „Näherung”:
- $$H(Z_{Y,\hspace{0.05cm} M = 8}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = 2\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 3\,{\rm bit}}\hspace{0.05cm}.$$
Man erhält wieder das gleiche Ergebnis wie bei der direkten Berechnung.
(6) Richtig ist nur die Aussage 1:
- Die Entropie $H(Z)$ einer diskreten Zufallsgröße $Z = \{z_1, \ \text{...} \ , z_M\}$ ist nie negativ.
- Der Grenzfall $H(Z) = 0$ ergibt sich zum Beispiel für ${\rm Pr}(Z = z_1) = 1$ und ${\rm Pr}(Z = z_\mu) = 0$ für $2 \le \mu \le M$.
- Dagegen kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ wie folgt sein:
- $h(X) < 0$ $($Teilaufgabe 1$)$,
- $h(X) > 0$ $($Teilaufgabe 2$)$, oder auch
- $h(X) = 0$ $($zum Beispiel für $x_{\rm min} = 0$ und $x_{\rm max} = 1)$.