Digitalsignalübertragung/Binary Symmetric Channel (BSC): Unterschied zwischen den Versionen
| Zeile 90: | Zeile 90: | ||
*ist die Anwendung des BSC–Modells oft gerechtfertigt, | *ist die Anwendung des BSC–Modells oft gerechtfertigt, | ||
*nicht jedoch, wenn Fadingeinflüsse $($[[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Rayleigh.E2.80.93_und_Riceverteilung|"Rayleigh oder Rice"$)$]] eine Rolle spielen | *nicht jedoch, wenn Fadingeinflüsse $($[[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Rayleigh.E2.80.93_und_Riceverteilung|"Rayleigh oder Rice"$)$]] eine Rolle spielen | ||
| − | *oder wenn Echos auftreten können ⇒ [[Mobile_Kommunikation/Mehrwegeempfang_beim_Mobilfunk|Mehrwegeempfang]].<br> | + | *oder wenn Echos auftreten können ⇒ [[Mobile_Kommunikation/Mehrwegeempfang_beim_Mobilfunk|"Mehrwegeempfang"]].<br> |
Aktuelle Version vom 5. September 2022, 14:07 Uhr
Inhaltsverzeichnis
Binary Symmetric Channel – Modell und Fehlerkorrelationsfunktion
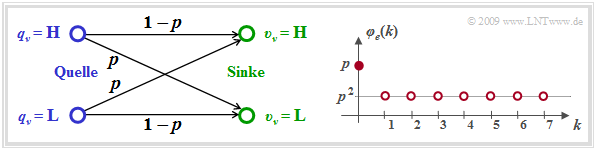
Die linke Grafik zeigt mit dem BSC–Modell das einfachste Modell eines digitalen Übertragungssystems.
Der Name steht für "Binary Symmetric Channel" und besagt, dass dieses Modell nur bei Binärsystemen mit symmetrischen Verfälschungseigenschaften angewendet werden kann. Weiter gilt:
- Das BSC–Modell eignet sich für die Untersuchung und Erzeugung einer Fehlerfolge mit statistisch unabhängigen Fehlern.
- Man nennt einen solchen Kanal "gedächtnisfrei". Im Unterschied zu den "Bündelfehler–Kanalmodellen" existiert hier nur ein einziger Kanalzustand.
- Die beiden Symbole $($zum Beispiel $\rm L$ und $\rm H)$ werden jeweils mit der gleichen Wahrscheinlichkeit $p$ verfälscht, so dass auch die mittlere Fehlerwahrscheinlichkeit $p_{\rm M} = p$ ist, und zwar unabhängig von den Symbolwahrscheinlichkeiten $p_{\rm L}$ und $p_{\rm H}$.
Die rechte Grafik zeigt die "Fehlerkorrelationsfunktion" $\rm (FKF)$ des BSC–Modells:
- \[\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big] = \left\{ \begin{array}{c} p \\ p^2 \end{array} \right.\quad \begin{array}{*{1}c} f{\rm \ddot{u}r }\hspace{0.25cm}k = 0 \hspace{0.05cm}, \\ f{\rm \ddot{u}r }\hspace{0.25cm} k > 0 \hspace{0.05cm}.\\ \end{array}\]
$\text{Fazit:}$
- Beim BSC–Modell wird der FKF–Endwert $($Quadrat der mittleren Fehlerwahrscheinlichkeit$)$, der bei anderen Modellen erst für $k \to \infty$ gültig ist, bereits bei $k = 1$ exakt erreicht und bleibt dann konstant.
- Das BSC–Modell gehört zur Klasse der "erneuernden Kanalmodelle" $($englisch: "renewal channels"). Bei einem erneuernden Kanalmodell sind die Fehlerabstände statistisch voneinander unabhängig und die Fehlerkorrelationsfunktion kann in einfacher Weise iterativ berechnet werden:
- \[\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa) \hspace{0.05cm}.\]
Binary Symmetric Channel – Fehlerabstandsverteilung
Wir betrachten nun die "Fehlerabstandsverteilung" $\rm (FAV)$. Die Wahrscheinlichkeit für den Fehlerabstand $a=k$ ergibt sich aus der Bedingung von $k-1$ fehlerfreien Symbolen und eines Übertragungsfehlers zum Zeitpunkt $\nu +k$, vorausgesetzt, dass der letzte Fehler zum Zeitpunkt $\nu$ aufgetreten ist. Man erhält:
- \[{\rm Pr}(a = k) = (1-p)^{k-1}\cdot p \hspace{0.05cm}.\]
Daraus folgt:
- Der Fehlerabstand $a = 1$ tritt beim BSC–Modell stets mit der größten Wahrscheinlichkeit auf, und zwar für jeden Wert von $p$.
- Dieser Sachverhalt ist auf den ersten Blick etwas überraschend:
Mit $p = 0.01$ ergibt sich zum Beispiel der mittlere Fehlerabstand ${\rm E}\big[a\big] = 100$. Trotzdem sind zwei aufeinanderfolgende Fehler $(a = 1)$ um den Faktor $0.99^{99} \approx 2.7$ wahrscheinlicher als der Fehlerabstand $a = 100$.
- Die Fehlerabstandsverteilung ergibt sich entsprechend der "allgemeinen Definition" durch Summation:
- \[V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} (1-p)^{\kappa-1}\cdot p = (1-p)^{k-1}\hspace{0.05cm}.\]
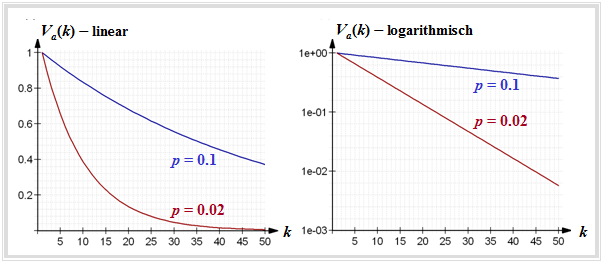
$\text{Beispiel 1:}$ Die linke Grafik zeigt $V_a(k)$ in linearer Darstellung für
- $p = 0.1$ (blaue Kurve), und
- $p = 0.02$ (rote Kurve).
⇒ Der Abfall erfolgt mit steigendem $k$ exponentiell und ist umso steiler, je kleiner $p$ ist.
⇒ Die rechte Grafik zeigt die logarithmische Darstellung. Hier verläuft der Abfall linear entsprechend
- \[{\rm lg} \hspace{0.15cm}V_a(k) = (k - 1) \cdot {\rm lg} \hspace{0.15cm}(1-p)\hspace{0.05cm}.\]
Anwendungen des BSC–Modells
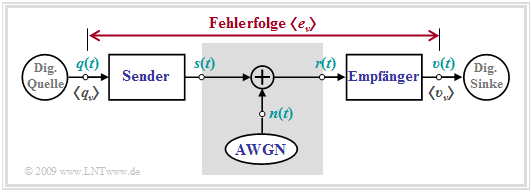
Das BSC–Modell ist das "digitale Äquivalent" zum einfachsten analogen Modell ⇒ "AWGN" für ein zeitinvariantes Digitalsystem entsprechend der folgenden Grafik.
- Einzige Beeinträchtigung ist das Rauschen.
- Es gibt keine Verzerrungen.
Um das BSC–Modell anwenden zu können, muss das Digitalsystem folgende Voraussetzungen erfüllen:
- Redundanzfreie Binärcodierung ⇒ keine Kanalcodierung und –decodierung,
- Störung entsprechend dem AWGN–Modell ⇒ additiv, weiß und gaußverteilt,
- keine Verzerrungen durch die Bauteile von Sender und Empfänger,
- Schwellenwertentscheider mit symmetrischer Entscheiderschwelle,
- keine Fremdeinflüsse wie:
Nebensprechen, Wählimpulse, elektromagnetische Störfelder ...
Bei einem "Funksystem" mit direkter Sichtverbindung "Sender – Empfänger"
- ist die Anwendung des BSC–Modells oft gerechtfertigt,
- nicht jedoch, wenn Fadingeinflüsse $($"Rayleigh oder Rice"$)$ eine Rolle spielen
- oder wenn Echos auftreten können ⇒ "Mehrwegeempfang".
⇒ Bei "leitungsgebundener Übertragung" $($zum Beispiel "DSL", aber auch bei optischer Übertragung$)$ sind dagegen nach Aussagen von Netzbetreibern statistisch unabhängige Fehler eher die Ausnahme.
⇒ Treten bei der Datenübertragung über das Fernsprechnetz Fehler auf, dann meist gehäuft. Man spricht in diesem Fall von so genannten "Bündelfehlern", die im nächsten Kapitel behandelt werden.
Aufgaben zum Kapitel
Aufgabe 5.3: AWGN- und BSC-Modell
Aufgabe 5.3Z: Analyse des BSC-Modell
Aufgabe 5.4: Ist das BSC-Modell erneuernd?
Aufgabe 5.5: Fehlerfolge und Fehlerabstandsfolge