Applets:Periodendauer periodischer Signale: Unterschied zwischen den Versionen
Höfler (Diskussion | Beiträge) |
|||
| (37 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{LntAppletLinkDeEn|signalPeriod|signalPeriod_en}} | |
| − | |||
| − | |||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
| − | Dieses Applet zeichnet den Verlauf und berechnet die Periodendauer $T_0$ der periodischen Funktion | + | <br> |
| + | Dieses Applet zeichnet den Verlauf und berechnet die Periodendauer $T_0$ der periodischen Funktion | ||
:$$x(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right).$$ | :$$x(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right).$$ | ||
Bitte beachten Sie: | Bitte beachten Sie: | ||
| − | *Die Phasen $\varphi_i$ sind hier im Bogenmaß einzusetzen. Umrechnung aus dem Eingabewert: $\varphi_i \text{[im Bogenmaß]} =\varphi_i \text{[in Grad]}/360 \cdot 2\pi$ | + | *Die Phasen $\varphi_i$ sind hier im Bogenmaß einzusetzen. Umrechnung aus dem Eingabewert: |
| − | *Ausgegeben werden auch der Maximalwert $x_{\rm max}$ und ein Signalwert $x(t_*)$ zu einer vorgebbaren Zeit $t_*$. | + | :$$\varphi_i \text{[im Bogenmaß]} =\varphi_i \text{[in Grad]}/360 \cdot 2\pi.$$ |
| − | *Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung. | + | *Ausgegeben werden auch der Maximalwert $x_{\rm max}$ und ein Signalwert $x(t_*)$ zu einer vorgebbaren Zeit $t_*$. |
| + | *Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung. | ||
| + | |||
| + | |||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| − | + | <br> | |
| − | + | Ein ''periodisches Signal'' $x(t)$ liegt genau dann vor, wenn dieses nicht konstant ist und für alle beliebigen Werte von $t$ und alle ganzzahligen Werte von $i$ mit einem geeigneten $T_{0}$ gilt: $x(t+i\cdot T_{0}) = x(t).$ | |
| + | *Man bezeichnet $T_0$ als die '''Periodendauer''' und $f_0 = 1/T_0$ als die '''Grundfrequenz'''. | ||
| − | *Bei einer harmonischen Schwingung $x_1(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)$ gilt $f_0 = f_1$ und $T_0 = 1/f_1$, unabhängig von der Phase $\varphi_1$ und der Amplitude $A_1 \ne 0$. | + | *Bei einer harmonischen Schwingung $x_1(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)$ gilt $f_0 = f_1$ und $T_0 = 1/f_1$, unabhängig von der Phase $\varphi_1$ und der Amplitude $A_1 \ne 0$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Berechnungsvorschrift:}$ Setzt sich das periodisches Signal $x(t)$ wie in diesem Applet aus zwei Anteilen $x_1(t)$ und $x_2(t)$ zusammen, dann gilt mit $A_1 \ne 0$, $f_1 \ne 0$, $A_2 \ne 0$, $f_2 \ne 0$ für Grundfrequenz und Periodendauer: | + | $\text{Berechnungsvorschrift:}$ Setzt sich das periodisches Signal $x(t)$ wie in diesem Applet aus zwei Anteilen $x_1(t)$ und $x_2(t)$ zusammen, dann gilt mit $A_1 \ne 0$, $f_1 \ne 0$, $A_2 \ne 0$, $f_2 \ne 0$ für Grundfrequenz und Periodendauer: |
| − | :$$f_0 = {\rm ggT}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0 | + | :$$f_0 = {\rm ggT}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0.$$ |
| − | + | Hierbei bezeichnet $\rm ggT$ den '''größten gemeinsamen Teiler'''.}} | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiele:}$ Im Folgenden bezeichnen $f_0'$, $f_1'$ und $f_2'$ | + | $\text{Beispiele:}$ Im Folgenden bezeichnen $f_0'$, $f_1'$ und $f_2'$ jeweils auf $1\ \rm kHz$ normierte Signalfrequenzen: |
'''(a)''' $f_1' = 1.0$, $f_2' = 3.0$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.0) = 1.0$ ⇒ $T_0 = 1.0\ \rm ms$; | '''(a)''' $f_1' = 1.0$, $f_2' = 3.0$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.0) = 1.0$ ⇒ $T_0 = 1.0\ \rm ms$; | ||
| − | '''(b)''' $f_1' = 1.0$, $f_2' = 3.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.5)= 0.5$ ⇒ $T_0 = 2\ \rm ms$; | + | '''(b)''' $f_1' = 1.0$, $f_2' = 3.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.5)= 0.5$ ⇒ $T_0 = 2.0\ \rm ms$; |
'''(c)''' $f_1' = 1.0$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 2.5) = 0.5$ ⇒ $T_0 = 2.0\ \rm ms$; | '''(c)''' $f_1' = 1.0$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 2.5) = 0.5$ ⇒ $T_0 = 2.0\ \rm ms$; | ||
| − | '''(d)''' $f_1' = 0.9$, $f_2' = | + | '''(d)''' $f_1' = 0.9$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(0.9, \ 2.5) = 0.1$ ⇒ $T_0 = 10.0 \ \rm ms$; |
| − | '''(e)''' $f_2' = \sqrt{2} \cdot f_1' $ ⇒ $f_0' = {\rm ggt}(f_1', \ f_2') \to 0$ ⇒ $T_0 \to \infty$ ⇒ Das Signal $x(t)$ ist nicht periodisch.}} | + | '''(e)''' $f_2' = \sqrt{2} \cdot f_1' $ ⇒ $f_0' = {\rm ggt}(f_1', \ f_2') \to 0$ ⇒ $T_0 \to \infty$ ⇒ Das Signal $x(t)$ ist nicht periodisch.}} |
| − | $\text{Anmerkung:}$ Die Periodendauer könnte auch als ''kleinstes | + | $\text{Anmerkung:}$ Die Periodendauer könnte auch als '''kleinstes gemeinsames Vielfaches''' $\rm (kgV)$ entsprechend $T_0 = {\rm kgV}(T_1, \ T_2)$ ermittelt werden: |
| − | '''(c)''' $T_1 = 1.0\ \rm ms$, $T_2 = 0.4\ \rm kHz$ ⇒ $ | + | :'''(c)''' $T_1 = 1.0\ \rm ms$, $T_2 = 0.4\ \rm kHz$ ⇒ $T_0 = {\rm kgV}(1.0, \ 0.4) \ \rm ms = 2.0\ \rm ms$ |
Bei allen anderen Parameterwerten würde es aber zu numerischen Problemen kommen, zum Beispiel | Bei allen anderen Parameterwerten würde es aber zu numerischen Problemen kommen, zum Beispiel | ||
| − | '''(a)''' $T_1 = 1.0\ \rm ms$ und $T_2 = 0.333\text{...} \ \rm ms$ besitzen aufgrund der begrenzten Darstellung reeller Zahlen kein kleinstes gemeinsames Vielfaches. | + | :'''(a)''' $T_1 = 1.0\ \rm ms$ und $T_2 = 0.333\text{...} \ \rm ms$ besitzen aufgrund der begrenzten Darstellung reeller Zahlen kein kleinstes gemeinsames Vielfaches. |
| + | |||
| + | ==Versuchsdurchführung== | ||
| + | <br> | ||
| + | *Wählen Sie zunächst die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht „Reset”: Einstellung wie beim Programmstart. | ||
| + | *Eine Aufgabenbeschreibung wird angezeigt. Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”. | ||
| + | *$A_1'$ und $A_2'$ bezeichnen hier die auf $1\ \rm V$ normierten Signalamplituden. $ f_0'$, $f_1'$ und $f_2'$ sind die auf $1\ \rm kHz$ normierten Frequenzen. | ||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' | + | '''(1)''' Es gelte $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 2.0, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ\text{.}$ Wie groß ist die Periodendauer $T_0$?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 2.0 \ \rm ms$ wegen ${\rm ggt}(2.0, 2.5) = 0.5$. | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 2.0 \ \rm ms$ wegen ${\rm ggt}(2.0, 2.5) = 0.5$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' Variieren Sie | + | '''(2)''' Variieren Sie $\varphi_1$ und $\varphi_2$ im gesamten möglichen Bereich $\pm 180^\circ\text{.}$ Wie wirkt sich dies auf die Periodendauer $T_0$ aus?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer $T_0 = 2.0 \ \rm ms$ bleibt erhalten. | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer $T_0 = 2.0 \ \rm ms$ bleibt für alle $\varphi_1$ und $\varphi_2$ erhalten. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' Wählen Sie die Voreinstellung | + | '''(3)''' Wählen Sie die Voreinstellung ⇒ „Recall Parameters”. Variieren Sie $A_1'$ im gesamten möglichen Bereich $0 \le A_1' \le 1$.}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer $T_0 = 2.0 \ \rm ms$ bleibt erhalten mit Ausnahme von $A_1' =0$. | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer $T_0 = 2.0 \ \rm ms$ bleibt erhalten mit Ausnahme von $A_1' =0$. In letzerem Fall ist $T_0 = 0.4 \ \rm ms$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' Wählen Sie die Voreinstellung $ | + | '''(4)''' Wählen Sie die Voreinstellung ⇒ „Recall Parameters” und variieren Sie $f_2' $? Hat dies Auswirkungen auf $T_0$? Welcher Wert ergibt sich für $f_2' = 0.2$.}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer springt hin und her. Für $f_2' = 0.2$ ergibt sich $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(2.0, 0.2) = 0.2$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(5)''' | + | '''(5)''' Es gelte $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 0.2, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ\text{.}$ Wie groß ist $T_0$? Speichern Sie diese Einstellung mit „Store Parameters”.}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 10.0 \ \rm ms$ wegen ${\rm ggt}(0.2, 2.5) = 0.1$. | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 10.0 \ \rm ms$ wegen ${\rm ggt}(0.2, 2.5) = 0.1$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' Wählen Sie die letzte Einstellung | + | '''(6)''' Wählen Sie die letzte Einstellung ⇒ „Recall Parameters” und ändern Sie $f_2' = 0.6$. Speichern Sie diese Einstellung mit „Store Parameters”:}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(0.2,0.6) = 0.2$. | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(0.2,0.6) = 0.2$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(7)''' Wie groß ist bei gleicher Einstellung der maximale Signalwert $x_{\rm max}\text{ | + | '''(7)''' Wie groß ist bei gleicher Einstellung der maximale Signalwert $x_{\rm max}\text{?}$}} |
| − | |||
| − | |||
| + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.38 \ {\rm V} < A_1 + A_2$ mit $t_* = 0.3 \ \rm ms$ und $T_0 = 5.0 \ \rm ms$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(8)''' | + | '''(8)''' Welcher Unterschied ergibt sich mit $\varphi_2 = 0^\circ \hspace{0.1cm}\Rightarrow\hspace{0.1cm}$ Summe zweier Cosinusschwingungen?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $t_* = 0$, $T_0 = 5.0 \ \rm ms$ ⇒ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.5 \ {\rm V}=A_1 + A_2$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(9)''' | + | '''(9)''' Nun gelte $\varphi_1 = \varphi_2 = 90^\circ \hspace{0.1cm}\Rightarrow\hspace{0.1cm}$ Summe zweier Sinusschwingungen. Wie groß ist hier der maximale Signalwert $x_{\rm max}\text{?}$}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist nun | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist nun $x_{\rm max} = 1.07 \ {\rm V} < A_1 + A_2$. Dieser Wert ergibt sich mit $T_0 = 5.0 \ \rm ms$ sowie $t_* = 0.6 \ \rm ms$ bzw. $t_* = 1.9 \ \rm ms$. |
| Zeile 101: | Zeile 107: | ||
==Zur Handhabung der Applet-Variante 1== | ==Zur Handhabung der Applet-Variante 1== | ||
| + | [[Datei:Anleitung_Periodendauer.png|right|frame|Bildschirmabzug der englischen Version]] | ||
| + | |||
| + | '''(A)''' Parametereingabe für Schwingung 1 | ||
| + | |||
| + | '''(B)''' Parametereingabe für Schwingung 2 und der Zeit $t_*$. | ||
| + | |||
| + | '''(C)''' Numerikausgabe des Hauptergebnisses $T_0$; graphische Verdeutlichung durch rote Linie | ||
| + | |||
| + | '''(D)''' Abspeichern von Parametersätzen | ||
| + | |||
| + | '''(E)''' Zurückholen von Parametersätzen | ||
| + | |||
| + | '''(F)''' Ausgabe von $x_{\rm max}$ und der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ | ||
| + | |||
| + | '''(G)''' Grafikfeld zur Darstellung der Signale | ||
| + | |||
| + | Die Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ werden durch grüne Punkte markiert | ||
| + | |||
| + | Am unteren rechten Grafikrand finden Sie folgende Buttos: | ||
| − | + | '''(1)''' Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen) | |
| + | '''(2)''' Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$” | ||
| + | '''(H)''' Aufgabenauswahl entsprechend der Aufgabennummer | ||
| + | <br><br> | ||
| + | In allen Applets oben rechts: Veränderbare grafische Oberflächengestaltung ⇒ '''Theme''': | ||
| + | * Dark: schwarzer Hintergrund (wird von den Autoren empfohlen) | ||
| + | * Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke) | ||
| + | * Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche | ||
| + | * Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche | ||
| + | <br clear = all> | ||
==Über die Autoren== | ==Über die Autoren== | ||
| − | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | + | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. |
| − | *Die erste Version wurde 2004 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]] ). | + | *Die erste Version wurde 2004 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]] ). |
| − | *2017 wurde dieses Programm von [[David Jobst]] im Rahmen seiner Ingenieurspraxis (Betreuer: [[Biografien_und_Bibliografien/ | + | *2017 wurde dieses Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#David_Jobst_.28Ingenieurspraxis_Math_2017.29|David Jobst]] im Rahmen seiner Ingenieurspraxis (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29|Tasnád Kernetzky]]) auf „HTML5” umgesetzt und neu gestaltet ⇒ Applet-Variante 1. Parallel dazu erarbeitete [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Bastian_Siebenwirth_.28Bachelorarbeit_LB_2017.29|Bastian Siebenwirth]] im Rahmen seiner Bachelorarbeit (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]) die HTML5-Variante 2. |
| − | |||
==Nochmalige Aufrufmöglichkeit der Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit der Applets in neuem Fenster== | ||
Wir bieten hier zwei Applets zur gleichen Thematik mit unterschiedlichem Layout an: | Wir bieten hier zwei Applets zur gleichen Thematik mit unterschiedlichem Layout an: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|signalPeriod|Applet-Variante 1 in neuem Tab öffnen}} {{LntAppletLink|signalPeriodS_en|Applet-Variante 2 in neuem Tab öffnen}} |
| − | |||
| − | |||
Aktuelle Version vom 26. Oktober 2023, 11:05 Uhr
Applet in neuem Tab öffnen Open English Version
Inhaltsverzeichnis
Programmbeschreibung
Dieses Applet zeichnet den Verlauf und berechnet die Periodendauer $T_0$ der periodischen Funktion
- $$x(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right).$$
Bitte beachten Sie:
- Die Phasen $\varphi_i$ sind hier im Bogenmaß einzusetzen. Umrechnung aus dem Eingabewert:
- $$\varphi_i \text{[im Bogenmaß]} =\varphi_i \text{[in Grad]}/360 \cdot 2\pi.$$
- Ausgegeben werden auch der Maximalwert $x_{\rm max}$ und ein Signalwert $x(t_*)$ zu einer vorgebbaren Zeit $t_*$.
- Das aufzurufende Applet verwendet die englischen Begriffe im Gegensatz zu dieser deutschen Beschreibung.
Theoretischer Hintergrund
Ein periodisches Signal $x(t)$ liegt genau dann vor, wenn dieses nicht konstant ist und für alle beliebigen Werte von $t$ und alle ganzzahligen Werte von $i$ mit einem geeigneten $T_{0}$ gilt: $x(t+i\cdot T_{0}) = x(t).$
- Man bezeichnet $T_0$ als die Periodendauer und $f_0 = 1/T_0$ als die Grundfrequenz.
- Bei einer harmonischen Schwingung $x_1(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)$ gilt $f_0 = f_1$ und $T_0 = 1/f_1$, unabhängig von der Phase $\varphi_1$ und der Amplitude $A_1 \ne 0$.
$\text{Berechnungsvorschrift:}$ Setzt sich das periodisches Signal $x(t)$ wie in diesem Applet aus zwei Anteilen $x_1(t)$ und $x_2(t)$ zusammen, dann gilt mit $A_1 \ne 0$, $f_1 \ne 0$, $A_2 \ne 0$, $f_2 \ne 0$ für Grundfrequenz und Periodendauer:
- $$f_0 = {\rm ggT}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0.$$
Hierbei bezeichnet $\rm ggT$ den größten gemeinsamen Teiler.
$\text{Beispiele:}$ Im Folgenden bezeichnen $f_0'$, $f_1'$ und $f_2'$ jeweils auf $1\ \rm kHz$ normierte Signalfrequenzen:
(a) $f_1' = 1.0$, $f_2' = 3.0$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.0) = 1.0$ ⇒ $T_0 = 1.0\ \rm ms$;
(b) $f_1' = 1.0$, $f_2' = 3.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 3.5)= 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;
(c) $f_1' = 1.0$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(1.0, \ 2.5) = 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;
(d) $f_1' = 0.9$, $f_2' = 2.5$ ⇒ $f_0' = {\rm ggt}(0.9, \ 2.5) = 0.1$ ⇒ $T_0 = 10.0 \ \rm ms$;
(e) $f_2' = \sqrt{2} \cdot f_1' $ ⇒ $f_0' = {\rm ggt}(f_1', \ f_2') \to 0$ ⇒ $T_0 \to \infty$ ⇒ Das Signal $x(t)$ ist nicht periodisch.
$\text{Anmerkung:}$ Die Periodendauer könnte auch als kleinstes gemeinsames Vielfaches $\rm (kgV)$ entsprechend $T_0 = {\rm kgV}(T_1, \ T_2)$ ermittelt werden:
- (c) $T_1 = 1.0\ \rm ms$, $T_2 = 0.4\ \rm kHz$ ⇒ $T_0 = {\rm kgV}(1.0, \ 0.4) \ \rm ms = 2.0\ \rm ms$
Bei allen anderen Parameterwerten würde es aber zu numerischen Problemen kommen, zum Beispiel
- (a) $T_1 = 1.0\ \rm ms$ und $T_2 = 0.333\text{...} \ \rm ms$ besitzen aufgrund der begrenzten Darstellung reeller Zahlen kein kleinstes gemeinsames Vielfaches.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht „Reset”: Einstellung wie beim Programmstart.
- Eine Aufgabenbeschreibung wird angezeigt. Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”.
- $A_1'$ und $A_2'$ bezeichnen hier die auf $1\ \rm V$ normierten Signalamplituden. $ f_0'$, $f_1'$ und $f_2'$ sind die auf $1\ \rm kHz$ normierten Frequenzen.
(1) Es gelte $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 2.0, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ\text{.}$ Wie groß ist die Periodendauer $T_0$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 2.0 \ \rm ms$ wegen ${\rm ggt}(2.0, 2.5) = 0.5$.
(2) Variieren Sie $\varphi_1$ und $\varphi_2$ im gesamten möglichen Bereich $\pm 180^\circ\text{.}$ Wie wirkt sich dies auf die Periodendauer $T_0$ aus?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer $T_0 = 2.0 \ \rm ms$ bleibt für alle $\varphi_1$ und $\varphi_2$ erhalten.
(3) Wählen Sie die Voreinstellung ⇒ „Recall Parameters”. Variieren Sie $A_1'$ im gesamten möglichen Bereich $0 \le A_1' \le 1$.
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer $T_0 = 2.0 \ \rm ms$ bleibt erhalten mit Ausnahme von $A_1' =0$. In letzerem Fall ist $T_0 = 0.4 \ \rm ms$.
(4) Wählen Sie die Voreinstellung ⇒ „Recall Parameters” und variieren Sie $f_2' $? Hat dies Auswirkungen auf $T_0$? Welcher Wert ergibt sich für $f_2' = 0.2$.
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer springt hin und her. Für $f_2' = 0.2$ ergibt sich $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(2.0, 0.2) = 0.2$.
(5) Es gelte $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 0.2, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ\text{.}$ Wie groß ist $T_0$? Speichern Sie diese Einstellung mit „Store Parameters”.
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 10.0 \ \rm ms$ wegen ${\rm ggt}(0.2, 2.5) = 0.1$.
(6) Wählen Sie die letzte Einstellung ⇒ „Recall Parameters” und ändern Sie $f_2' = 0.6$. Speichern Sie diese Einstellung mit „Store Parameters”:
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Die Periodendauer ist $T_0 = 5.0 \ \rm ms$ wegen ${\rm ggt}(0.2,0.6) = 0.2$.
(7) Wie groß ist bei gleicher Einstellung der maximale Signalwert $x_{\rm max}\text{?}$
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.38 \ {\rm V} < A_1 + A_2$ mit $t_* = 0.3 \ \rm ms$ und $T_0 = 5.0 \ \rm ms$.
(8) Welcher Unterschied ergibt sich mit $\varphi_2 = 0^\circ \hspace{0.1cm}\Rightarrow\hspace{0.1cm}$ Summe zweier Cosinusschwingungen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $t_* = 0$, $T_0 = 5.0 \ \rm ms$ ⇒ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.5 \ {\rm V}=A_1 + A_2$.
(9) Nun gelte $\varphi_1 = \varphi_2 = 90^\circ \hspace{0.1cm}\Rightarrow\hspace{0.1cm}$ Summe zweier Sinusschwingungen. Wie groß ist hier der maximale Signalwert $x_{\rm max}\text{?}$
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$Der maximale Signalwert ist nun $x_{\rm max} = 1.07 \ {\rm V} < A_1 + A_2$. Dieser Wert ergibt sich mit $T_0 = 5.0 \ \rm ms$ sowie $t_* = 0.6 \ \rm ms$ bzw. $t_* = 1.9 \ \rm ms$.
Zur Handhabung der Applet-Variante 1
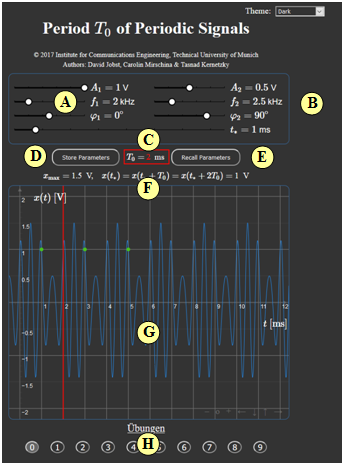
(A) Parametereingabe für Schwingung 1
(B) Parametereingabe für Schwingung 2 und der Zeit $t_*$.
(C) Numerikausgabe des Hauptergebnisses $T_0$; graphische Verdeutlichung durch rote Linie
(D) Abspeichern von Parametersätzen
(E) Zurückholen von Parametersätzen
(F) Ausgabe von $x_{\rm max}$ und der Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
(G) Grafikfeld zur Darstellung der Signale
Die Signalwerte $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ werden durch grüne Punkte markiert
Am unteren rechten Grafikrand finden Sie folgende Buttos:
(1) Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
(2) Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
(H) Aufgabenauswahl entsprechend der Aufgabennummer
In allen Applets oben rechts: Veränderbare grafische Oberflächengestaltung ⇒ Theme:
- Dark: schwarzer Hintergrund (wird von den Autoren empfohlen)
- Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke)
- Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche
- Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2004 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder ).
- 2017 wurde dieses Programm von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet ⇒ Applet-Variante 1. Parallel dazu erarbeitete Bastian Siebenwirth im Rahmen seiner Bachelorarbeit (Betreuer: Günter Söder) die HTML5-Variante 2.
Nochmalige Aufrufmöglichkeit der Applets in neuem Fenster
Wir bieten hier zwei Applets zur gleichen Thematik mit unterschiedlichem Layout an:
Applet-Variante 1 in neuem Tab öffnen Applet-Variante 2 in neuem Tab öffnen