Modulationsverfahren/Rauscheinfluss bei Winkelmodulation: Unterschied zwischen den Versionen
Aus LNTwww
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Winkelmodulation und WM–Demodulation |Vorherige Seite=Frequenzmodulation (FM) |Nächste Seite=Pulscodemodulation }} ==Signal–zu–Ra…“) |
|||
| Zeile 18: | Zeile 18: | ||
| − | [[Datei: | + | [[Datei:P_ID1107__Mod_T_3_3_S1_neu.png | SNR bei Phasenmodulation]] |
| + | |||
| + | |||
| + | Ist die Leistungskenngröße | ||
| + | $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ | ||
| + | |||
| + | Das bedeutet, dass das Sinken–SNR mit wachsendem $η$ quadratisch zunimmt. | ||
| + | |||
| + | Die exakte Berechnung von $ρ_υ$ ist nicht ganz einfach und auch langwierig. Hier soll nur der Rechenweg kurz geschildert werden: | ||
| + | *Man approximiert das weiße Rauschen $n(t)$ mit der Bandbreite $B_{\rm HF}$ durch eine Summe von Sinusstörern im Abstand $f_{\rm St}$ (siehe Skizze im nächsten Abschnitt). | ||
| + | *Man berechnet für jeden einzelnen Sinusstörer das S/N–Verhältnis nach der Demodulation und addiert die einzelnen Beiträge, die nun alle im Tiefpassbereich $|f| < B_{\rm NF}$ liegen. | ||
| + | *Das obige einfache Ergebnis erhält man nach dem Grenzübergang $f_{\rm St} →$ 0. Die Summe geht dann in ein Integral über und dieses kann unter Ausnutzung einiger Näherungen gelöst werden. | ||
Version vom 19. Juni 2016, 18:30 Uhr
Signal–zu–Rausch–Leistungsverhältnis bei PM
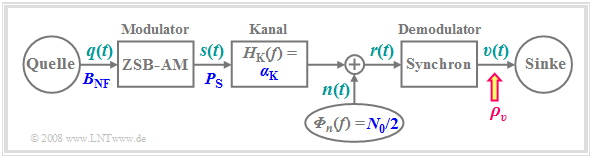
Zur Untersuchung des Rauschverhaltens gehen wir wieder vom so genannten AWGN–Kanal aus und berechnen das Sinken–SNR $ρ_υ$ in Abhängigkeit
- der Frequenz (Bandbreite) $B_{\rm NF}$ des cosinusförmigen Quellensignals,
- der Sendeleistung $P_{\rm S}$,
- des Kanaldämpfungsfaktors $α_{\rm K}$, und
- der (einseitigen) Rauschleistungsdichte $N_0$.
Eine ausführliche Modellbeschreibung findet man im Kapitel 1.2.
Ist die Leistungskenngröße
$$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
Das bedeutet, dass das Sinken–SNR mit wachsendem $η$ quadratisch zunimmt.
Die exakte Berechnung von $ρ_υ$ ist nicht ganz einfach und auch langwierig. Hier soll nur der Rechenweg kurz geschildert werden:
- Man approximiert das weiße Rauschen $n(t)$ mit der Bandbreite $B_{\rm HF}$ durch eine Summe von Sinusstörern im Abstand $f_{\rm St}$ (siehe Skizze im nächsten Abschnitt).
- Man berechnet für jeden einzelnen Sinusstörer das S/N–Verhältnis nach der Demodulation und addiert die einzelnen Beiträge, die nun alle im Tiefpassbereich $|f| < B_{\rm NF}$ liegen.
- Das obige einfache Ergebnis erhält man nach dem Grenzübergang $f_{\rm St} →$ 0. Die Summe geht dann in ein Integral über und dieses kann unter Ausnutzung einiger Näherungen gelöst werden.