Aufgaben:Aufgabe 4.4Z: Störabstand bei PCM: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
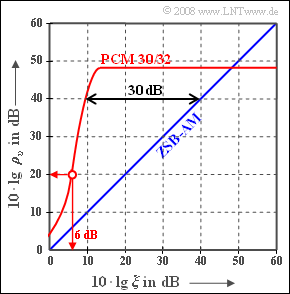
| − | [[Datei:P_ID1619__Mod_Z_4_4.png|right|frame|Störabstand von PCM 30/32 im Vergleich | + | [[Datei:P_ID1619__Mod_Z_4_4.png|right|frame|Störabstand von PCM 30/32 im Vergleich zur ZSB–Amplitudenmodulation]] |
| − | Die Grafik zeigt den Sinken–Störabstand $10 · \lg \ ρ_v$ für die Pulscodemodulation (PCM) im Vergleich zur analogen Zweiseitenband–Amplitudenmodulation, abgekürzt mit ZSB–AM. Für letztere gilt $ρ_v = ξ$, wobei die Leistungskenngröße | + | Die Grafik zeigt den Sinken–Störabstand $10 · \lg \ ρ_v$ für die Pulscodemodulation $\rm (PCM)$ im Vergleich zur analogen Zweiseitenband–Amplitudenmodulation, abgekürzt mit $\rm ZSB–AM$. |
| − | :$$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} | + | |
| + | Für letztere gilt $ρ_v = ξ$, wobei die Leistungskenngröße | ||
| + | :$$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} $$ | ||
folgende Systemparameter zusammenfasst: | folgende Systemparameter zusammenfasst: | ||
| − | :* den frequenzunabhängigen | + | :* den frequenzunabhängigen Übertragungsfaktor $α$ des Übertragungskanals, |
| − | :* die Leistung $P_{\rm S}$ des Sendsignals $s(t)$, auch kurz Sendeleistung genannt, | + | :* die Leistung $P_{\rm S}$ des Sendsignals $s(t)$, auch kurz "Sendeleistung" genannt, |
| − | :* die Nachrichtenfrequenz $f_{\rm N}$ (Bandbreite) des cosinusförmigen Quellensignals $q(t)$, | + | :* die Nachrichtenfrequenz $f_{\rm N}$ (Bandbreite) des cosinusförmigen Quellensignals $q(t)$, |
| − | :* die Rauschleistungsdichte $N_0$ des AWGN–Rauschens. | + | :* die (einseitige) Rauschleistungsdichte $N_0$ des AWGN–Rauschens. |
| − | Für das PCM–System wurde auf der Seite [[Modulationsverfahren/Pulscodemodulation#Absch.C3.A4tzung_der_SNR-Degradation_durch_.C3.9Cbertragungsfehler|Abschätzung der SNR-Degradation durch Übertragungsfehler]] folgende Näherung für das Sinken–SNR angegeben, die auch | + | Für das PCM–System wurde auf der Seite [[Modulationsverfahren/Pulscodemodulation#Absch.C3.A4tzung_der_SNR-Degradation_durch_.C3.9Cbertragungsfehler|"Abschätzung der SNR-Degradation durch Übertragungsfehler"]] folgende Näherung für das Sinken–SNR angegeben, die auch Übertragungsfehler aufgrund des AWGN–Rauschens berücksichtigt: |
:$$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$ | :$$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$ | ||
| − | Hierbei bezeichnet $N$ die Anzahl der Bit pro Abtastwert und $p_{\rm B}$ die Bitfehlerwahrscheinlichkeit. Da $ξ$ bei digitaler Modulation auch als die | + | *Hierbei bezeichnet $N$ die Anzahl der Bit pro Abtastwert und $p_{\rm B}$ die Bitfehlerwahrscheinlichkeit. |
| + | * Da die Leistungskenngröße $ξ$ bei digitaler Modulation auch als die "Signalenergie pro Bit" bezogen auf die "Rauschleistungsdichte" $(E_{\rm B}/N_0)$ interpretiert werden kann, gilt mit dem komplementären Gaußschen Fehlersignal ${\rm Q}(x)$ näherungsweise: | ||
:$$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$ | :$$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Pulscodemodulation|Pulscodemodulation]]. | + | |
| − | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Pulscodemodulation#Einfluss_von_.C3.9Cbertragungsfehlern|Einfluss von Übertragungsfehlern]] und [[Modulationsverfahren/Pulscodemodulation#Absch.C3.A4tzung_der_SNR-Degradation_durch_.C3.9Cbertragungsfehler|Abschätzung der SNR-Degradation durch Übertragungsfehler]]. | + | |
| − | *Bei der hier betrachteten PCM handelt es sich um die PCM 30/32, deren Systemparameter zum Beispiel in der [[Aufgaben:4.1_PCM–System_30/32 |Aufgabe 4.1]] angegeben sind. | + | Hinweise: |
| − | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Pulscodemodulation|"Pulscodemodulation"]]. | |
| + | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Pulscodemodulation#Einfluss_von_.C3.9Cbertragungsfehlern|"Einfluss von Übertragungsfehlern"]] und [[Modulationsverfahren/Pulscodemodulation#Absch.C3.A4tzung_der_SNR-Degradation_durch_.C3.9Cbertragungsfehler|"Abschätzung der SNR-Degradation durch Übertragungsfehler"]]. | ||
| + | *Bei der hier betrachteten PCM handelt es sich um die '''PCM 30/32''', deren Systemparameter zum Beispiel in der [[Aufgaben:4.1_PCM–System_30/32 |Aufgabe 4.1]] angegeben sind. | ||
| + | |||
| Zeile 29: | Zeile 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wieviele Bit pro Abtastwert ⇒ $N = N_1$ verwendet das betrachtete PCM–System? | + | {Wieviele Bit pro Abtastwert ⇒ $N = N_1$ verwendet das betrachtete PCM–System? |
|type="{}"} | |type="{}"} | ||
$N_1 \ = \ $ { 8 3% } | $N_1 \ = \ $ { 8 3% } | ||
| − | {Wieviele Bit pro Abtastwert ⇒ $N = N_2$ müsste man verwenden, damit $10 · \lg \ ρ_v > 64 \ \rm dB$ (Musikqualität) erreicht wird? | + | {Wieviele Bit pro Abtastwert ⇒ $N = N_2$ müsste man verwenden, damit $10 · \lg \ ρ_v > 64 \ \rm dB$ ("Musikqualität") erreicht wird? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_2 \ = \ $ { 11 3% } |
| − | {Welche (logarithmierte) Leistungskenngröße $ξ_{40\ \rm dB}$ ist erforderlich, damit bei 8–Bit–PCM der Sinkenstörabstand gleich $40\ \rm dB$ ist? | + | {Welche (logarithmierte) Leistungskenngröße $ξ_{40\ \rm dB}$ ist erforderlich, damit bei 8–Bit–PCM der Sinkenstörabstand gleich $40\ \rm dB$ ist? |
|type="{}"} | |type="{}"} | ||
$10 · \lg \ ξ_{40\ \rm dB} \ = \ $ { 10 3% } $\ \rm dB$ | $10 · \lg \ ξ_{40\ \rm dB} \ = \ $ { 10 3% } $\ \rm dB$ | ||
| − | {Um welchen Faktor könnte man bei PCM die Sendeleistung gegenüber der | + | {Um welchen Faktor könnte man bei PCM die Sendeleistung gegenüber der ZSB–AM reduzieren, um trotzdem $10 · \lg \ ρ_v = 40\ \rm dB$ zu erreichen? |
|type="{}"} | |type="{}"} | ||
$K_\text{AM → PCM} \ = \ $ { 1000 3% } | $K_\text{AM → PCM} \ = \ $ { 1000 3% } | ||
| − | {Welche Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ergibt sich für $10 · \lg \ ξ = 6\ \rm dB$ und $N = N_1$ ⇒ Ergebnis | + | {Welche Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ergibt sich für $10 · \lg \ ξ = 6\ \rm dB$ und $N = N_1$ ⇒ Ergebnis der Teilaufgabe '''(1)'''? |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm B} \ = \ $ { | + | $p_{\rm B} \ = \ $ { 2.5 3% } $\ \%$ |
| − | {Welches SNR würde sich bei gleichem $ξ$ mit einer 3–Bit–PCM ⇒ $N = 3$ ergeben? | + | {Welches SNR würde sich bei gleichem $ξ$ mit einer 3–Bit–PCM ⇒ $N = 3$ ergeben? |
|type="{}"} | |type="{}"} | ||
$10 · \lg \ ρ_v \ = \ $ { 15.9 3% } $\ \rm dB$ | $10 · \lg \ ρ_v \ = \ $ { 15.9 3% } $\ \rm dB$ | ||
| Zeile 57: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Der horizontale Abschnitt der PCM–Kurve wird allein durch das Quantisierungsrauschen bestimmt. |
| − | $$ \rho_{v} (\xi \rightarrow \infty) = \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{v} \approx 6\,{\rm dB} \cdot N\hspace{0.05cm}.$$ | + | *Hier gilt mit der Quantisierungsstufenzahl $M = 2^N$: |
| − | Aus dem ablesbaren Störabstand $10 · lg | + | :$$ \rho_{v} (\xi \rightarrow \infty) = \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{v} \approx 6\,{\rm dB} \cdot N\hspace{0.05cm}.$$ |
| + | *Aus dem ablesbaren Störabstand $10 · \lg \ ρ_v ≈ 48 \ \rm dB$ folgt daraus $N_1\hspace{0.15cm}\underline { = 8}$ Bit pro Abtastwert und für die Quantisierungsstufenzahl $M = 256$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Aus der obigen Näherung erhält man für $N_2\hspace{0.15cm}\underline { = 11}$ Bit pro Abtastwert ⇒ $M = 2048$ den Störabstand $66 \ \rm dB$. | ||
| + | *Mit $N = 10$ ⇒ $M = 1024$ erreicht man nur ca. $60 \ \rm dB$. | ||
| + | *Bei der Compact Disc $\rm (CD)$ werden die PCM–Parameter $N = 16$ ⇒ $M = 65536$ ⇒ $10 · \lg \ ρ_v > 96 \ \rm dB$ verwendet. | ||
| + | |||
| + | |||
| + | '''(3)''' Bei Zweiseitenband–Amplitudenmodulation wären hierfür $10 · \lg \ ξ = 40\ \rm dB$ erforderlich. | ||
| + | *Wie aus der Grafik auf der Angabenseite hervorgeht, ist dieser Abszissenwert für die vorgegebene PCM um $30 \ \rm dB$ geringer ⇒ $10 · \lg \ ξ_{40\ \rm dB}\hspace{0.15cm}\underline { = 10 \ \rm dB}$. | ||
| − | |||
| − | ''' | + | '''(4)''' Der logarithmische Wert $30 \ \rm dB$ entspricht einer um den Faktor $10^3\hspace{0.15cm}\underline { = 1000}$ reduzierten Leistung. |
| − | |||
| + | '''(5)''' Aus der Grafik auf der Angabenseite erkennt man, dass der Abszissenwert $10 · \lg \ ξ= 6 \ \rm dB$ den Störabstand $20 \ \rm dB$ zur Folge hat. | ||
| + | *Aus $10 · \lg \ ρ_v = 20 \ \rm dB$ folgt $ρ_v = 100$ und damit weiter $($mit $N = N_1 = 8)$: | ||
| + | :$$\rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \approx \frac{1}{ 1.5 \cdot 10^{-5} + 4 \cdot p_{\rm B}} = 100 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} p_{\rm B} = \frac{0.01 - 1.5 \cdot 10^{-5}}{ 4} \hspace{0.15cm}\underline {\approx 2.5\%} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''6 | + | '''(6)''' Bei gleichem $ξ$ ist die Bitfehlerwahrscheinlichkeit weiterhin $p_{\rm B} = 0.025$. Damit erhält man mit $N = 3$ (Bit pro Abtastwert): |
| − | $$\rho_{\upsilon}= \frac{1}{ 2^{-6 } + 4 \cdot p_{\rm B}} = \frac{1}{ 0.015625 + 0.01} \approx 39 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\upsilon}\hspace{0.15cm}\underline {\approx 15.9\,{\rm dB}} \hspace{0.05cm}.$$ | + | :$$\rho_{\upsilon}= \frac{1}{ 2^{-6 } + 4 \cdot p_{\rm B}} = \frac{1}{ 0.015625 + 0.01} \approx 39 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\upsilon}\hspace{0.15cm}\underline {\approx 15.9\,{\rm dB}} \hspace{0.05cm}.$$ |
| − | + | Weiter ist anzumerken: | |
| + | *Auch bei nur drei Bit pro Abtastwert ist die Quantisierungsrauschleistung $(P_{\rm Q} = 0.015625)$ schon größer als die Fehlerrauschleistung $(P_{\rm F} = 0.01)$. | ||
| + | *Durch Erhöhung der Sendeleistung könnte wegen der Quantisierung der Sinkenstörabstand maximal $10 · \lg \ ρ_v =18 \ \rm dB$ betragen, wenn keine Bitfehler vorkommen $(P_{\rm F} = 0)$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 9. April 2022, 13:54 Uhr
Die Grafik zeigt den Sinken–Störabstand $10 · \lg \ ρ_v$ für die Pulscodemodulation $\rm (PCM)$ im Vergleich zur analogen Zweiseitenband–Amplitudenmodulation, abgekürzt mit $\rm ZSB–AM$.
Für letztere gilt $ρ_v = ξ$, wobei die Leistungskenngröße
- $$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} $$
folgende Systemparameter zusammenfasst:
- den frequenzunabhängigen Übertragungsfaktor $α$ des Übertragungskanals,
- die Leistung $P_{\rm S}$ des Sendsignals $s(t)$, auch kurz "Sendeleistung" genannt,
- die Nachrichtenfrequenz $f_{\rm N}$ (Bandbreite) des cosinusförmigen Quellensignals $q(t)$,
- die (einseitige) Rauschleistungsdichte $N_0$ des AWGN–Rauschens.
Für das PCM–System wurde auf der Seite "Abschätzung der SNR-Degradation durch Übertragungsfehler" folgende Näherung für das Sinken–SNR angegeben, die auch Übertragungsfehler aufgrund des AWGN–Rauschens berücksichtigt:
- $$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$
- Hierbei bezeichnet $N$ die Anzahl der Bit pro Abtastwert und $p_{\rm B}$ die Bitfehlerwahrscheinlichkeit.
- Da die Leistungskenngröße $ξ$ bei digitaler Modulation auch als die "Signalenergie pro Bit" bezogen auf die "Rauschleistungsdichte" $(E_{\rm B}/N_0)$ interpretiert werden kann, gilt mit dem komplementären Gaußschen Fehlersignal ${\rm Q}(x)$ näherungsweise:
- $$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Pulscodemodulation".
- Bezug genommen wird insbesondere auf die Seiten "Einfluss von Übertragungsfehlern" und "Abschätzung der SNR-Degradation durch Übertragungsfehler".
- Bei der hier betrachteten PCM handelt es sich um die PCM 30/32, deren Systemparameter zum Beispiel in der Aufgabe 4.1 angegeben sind.
Fragebogen
Musterlösung
- Hier gilt mit der Quantisierungsstufenzahl $M = 2^N$:
- $$ \rho_{v} (\xi \rightarrow \infty) = \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{v} \approx 6\,{\rm dB} \cdot N\hspace{0.05cm}.$$
- Aus dem ablesbaren Störabstand $10 · \lg \ ρ_v ≈ 48 \ \rm dB$ folgt daraus $N_1\hspace{0.15cm}\underline { = 8}$ Bit pro Abtastwert und für die Quantisierungsstufenzahl $M = 256$.
(2) Aus der obigen Näherung erhält man für $N_2\hspace{0.15cm}\underline { = 11}$ Bit pro Abtastwert ⇒ $M = 2048$ den Störabstand $66 \ \rm dB$.
- Mit $N = 10$ ⇒ $M = 1024$ erreicht man nur ca. $60 \ \rm dB$.
- Bei der Compact Disc $\rm (CD)$ werden die PCM–Parameter $N = 16$ ⇒ $M = 65536$ ⇒ $10 · \lg \ ρ_v > 96 \ \rm dB$ verwendet.
(3) Bei Zweiseitenband–Amplitudenmodulation wären hierfür $10 · \lg \ ξ = 40\ \rm dB$ erforderlich.
- Wie aus der Grafik auf der Angabenseite hervorgeht, ist dieser Abszissenwert für die vorgegebene PCM um $30 \ \rm dB$ geringer ⇒ $10 · \lg \ ξ_{40\ \rm dB}\hspace{0.15cm}\underline { = 10 \ \rm dB}$.
(4) Der logarithmische Wert $30 \ \rm dB$ entspricht einer um den Faktor $10^3\hspace{0.15cm}\underline { = 1000}$ reduzierten Leistung.
(5) Aus der Grafik auf der Angabenseite erkennt man, dass der Abszissenwert $10 · \lg \ ξ= 6 \ \rm dB$ den Störabstand $20 \ \rm dB$ zur Folge hat.
- Aus $10 · \lg \ ρ_v = 20 \ \rm dB$ folgt $ρ_v = 100$ und damit weiter $($mit $N = N_1 = 8)$:
- $$\rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \approx \frac{1}{ 1.5 \cdot 10^{-5} + 4 \cdot p_{\rm B}} = 100 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} = \frac{0.01 - 1.5 \cdot 10^{-5}}{ 4} \hspace{0.15cm}\underline {\approx 2.5\%} \hspace{0.05cm}.$$
(6) Bei gleichem $ξ$ ist die Bitfehlerwahrscheinlichkeit weiterhin $p_{\rm B} = 0.025$. Damit erhält man mit $N = 3$ (Bit pro Abtastwert):
- $$\rho_{\upsilon}= \frac{1}{ 2^{-6 } + 4 \cdot p_{\rm B}} = \frac{1}{ 0.015625 + 0.01} \approx 39 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\upsilon}\hspace{0.15cm}\underline {\approx 15.9\,{\rm dB}} \hspace{0.05cm}.$$
Weiter ist anzumerken:
- Auch bei nur drei Bit pro Abtastwert ist die Quantisierungsrauschleistung $(P_{\rm Q} = 0.015625)$ schon größer als die Fehlerrauschleistung $(P_{\rm F} = 0.01)$.
- Durch Erhöhung der Sendeleistung könnte wegen der Quantisierung der Sinkenstörabstand maximal $10 · \lg \ ρ_v =18 \ \rm dB$ betragen, wenn keine Bitfehler vorkommen $(P_{\rm F} = 0)$.