Digitalsignalübertragung/Blockweise Codierung mit 4B3T-Codes: Unterschied zwischen den Versionen
| (13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
== Allgemeine Beschreibung von Blockcodes == | == Allgemeine Beschreibung von Blockcodes == | ||
<br> | <br> | ||
| − | Bei '''Blockcodierung''' wird jeweils eine Sequenz von $m_q$ binären Quellensymbolen $(M_q = 2)$ durch einen Block von $m_c$ Codesymbolen mit dem Symbolumfang $M_c$ dargestellt. Um eine jede Quellensymbolfolge $\langle q_\nu \rangle$ in eine | + | Bei '''Blockcodierung''' wird jeweils eine Sequenz von $m_q$ binären Quellensymbolen $(M_q = 2)$ durch einen Block von $m_c$ Codesymbolen mit dem Symbolumfang $M_c$ dargestellt. Um eine jede Quellensymbolfolge $\langle q_\nu \rangle$ in eine Codesymbolfolge $\langle c_\nu \rangle$ umsetzen zu können, muss folgende Bedingung erfüllt sein: |
:$$M_c^{\hspace{0.1cm}m_c} \ge | :$$M_c^{\hspace{0.1cm}m_c} \ge | ||
M_q^{\hspace{0.1cm}m_q}\hspace{0.05cm}.$$ | M_q^{\hspace{0.1cm}m_q}\hspace{0.05cm}.$$ | ||
| − | Bei den im letzten Kapitel behandelten [[Digitalsignal%C3%BCbertragung/Redundanzfreie_Codierung|redundanzfreien Codes]] gilt in dieser Gleichung das Gleichheitszeichen, wenn$M_q$ eine Zweierpotenz ist. Mit dem Größerzeichen ergibt sich ein redundantes Digitalsignal, wobei die relative Coderedundanz wie folgt berechnet werden kann: | + | *Bei den im letzten Kapitel behandelten [[Digitalsignal%C3%BCbertragung/Redundanzfreie_Codierung|redundanzfreien Codes]] gilt in dieser Gleichung das Gleichheitszeichen, wenn $M_q$ eine Zweierpotenz ist. |
| + | |||
| + | *Mit dem Größerzeichen ergibt sich ein redundantes Digitalsignal, wobei die ''relative Coderedundanz'' wie folgt berechnet werden kann: | ||
:$$r_c = 1- \frac{m_q \cdot {\rm log_2}\hspace{0.05cm} (M_q)}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)} > 0 \hspace{0.05cm}.$$ | :$$r_c = 1- \frac{m_q \cdot {\rm log_2}\hspace{0.05cm} (M_q)}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)} > 0 \hspace{0.05cm}.$$ | ||
| − | Der bekannteste Blockcode zur Übertragungscodierung ist der '''4B3T–Code''' mit den Codeparametern | + | Der bekannteste Blockcode zur Übertragungscodierung ist der '''4B3T–Code''' mit den Codeparametern |
:$$m_q = 4,\hspace{0.2cm}M_q = 2,\hspace{0.2cm}m_c = | :$$m_q = 4,\hspace{0.2cm}M_q = 2,\hspace{0.2cm}m_c = | ||
3,\hspace{0.2cm}M_c = 3\hspace{0.05cm},$$ | 3,\hspace{0.2cm}M_c = 3\hspace{0.05cm},$$ | ||
| − | der bereits in den 1970–er Jahren entwickelt wurde und beispielsweise bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN| ISDN]] ( | + | der bereits in den 1970–er Jahren entwickelt wurde und beispielsweise bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN| ISDN]] ("Integrated Services Digital Networks") eingesetzt wird. |
| − | |||
| − | |||
| − | Die Umcodierung der sechzehn möglichen Binärblöcke in die entsprechenden Ternärblöcke könnte prinzipiell nach einer festen Codetabelle vorgenommen werden. Um die spektralen Eigenschaften dieser Codes weiter zu verbessern, werden bei den gebräuchlichen 4B3T–Codes, nämlich | + | Ein 4B3T–Code besitzt folgende Eigenschaften: |
| + | *Wegen $m_q \cdot T_{\rm B} = m_c \cdot T$ ist die Symboldauer $T$ des Codersignals um den Faktor $4/3$ größer als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Daraus ergibt sich die günstige Eigenschaft, dass der Bandbreitenbedarf um ein Viertel geringer ist als bei redundanzfreier Binärübertragung. | ||
| + | |||
| + | *Die relative Redundanz kann mit obiger Gleichung berechnet werden und ergibt sich zu $r_c \approx 16\%$. Diese Redundanz wird beim 4B3T–Code dazu verwendet, um Gleichsignalfreiheit zu erzielen. | ||
| + | |||
| + | *Das 4B3T–codierte Signal kann somit ohne merkbare Beeinträchtigung auch über einen Kanal mit der Eigenschaft $H_{\rm K}(f)= 0) = 0$ übertragen werden. | ||
| + | |||
| + | |||
| + | Die Umcodierung der sechzehn möglichen Binärblöcke in die entsprechenden Ternärblöcke könnte prinzipiell nach einer festen Codetabelle vorgenommen werden. Um die spektralen Eigenschaften dieser Codes weiter zu verbessern, werden bei den gebräuchlichen 4B3T–Codes, nämlich | ||
*dem 4B3T–Code nach Jessop und Waters,<br> | *dem 4B3T–Code nach Jessop und Waters,<br> | ||
| − | *dem MS43–Code (von: $\rm M$onitored $\rm S$um $\rm 4$B$\rm 3$T–Code),<br> | + | *dem MS43–Code (von: $\rm M$onitored $\rm S$um $\rm 4$B$\rm 3$T–Code),<br> |
| − | *dem FoMoT–Code (von: $\rm Fo$ur $\rm Mo$de $\rm T$ernary),<br><br> | + | *dem FoMoT–Code (von: $\rm Fo$ur $\rm Mo$de $\rm T$ernary),<br><br> |
| − | zwei oder mehrere Codetabellen verwendet, deren Auswahl von der | + | zwei oder mehrere Codetabellen verwendet, deren Auswahl von der "laufenden digitalen Summe" der Amplitudenkoeffizienten gesteuert wird. |
| + | |||
| + | Das Prinzip wird auf der nächsten Seite erklärt.<br> | ||
== Laufende digitale Summe == | == Laufende digitale Summe == | ||
<br> | <br> | ||
| − | Nach der Übertragung von | + | Nach der Übertragung von $l$ codierten Blöcken gilt für die "laufende digitale Summe" mit den ternären Amplitudenkoeffizienten $a_\nu \in \{ -1, 0, +1\}$: |
| + | [[Datei:P_ID1334__Dig_T_2_3_S2.png|right|frame|Codetabellen für drei 4B3T-Codes|class=fit]] | ||
:$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot | :$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot | ||
\hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}.$$ | \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}.$$ | ||
| − | Die Auswahl der Tabelle zur Codierung des $(l + 1)$–ten Blocks erfolgt abhängig vom aktuellen Wert $\ | + | Die Auswahl der Tabelle zur Codierung des $(l + 1)$–ten Blocks erfolgt abhängig vom aktuellen Wert ${\it \Sigma}_l$. |
| − | + | In der Tabelle sind die Codierregeln für die drei oben genannten 4B3T–Codes angegeben. Zur Vereinfachung der Schreibweise steht | |
| + | *„+” für den Amplitudenkoeffizienten „+1” und | ||
| + | *„–” für den Koeffizienten „–1”.<br> | ||
| − | + | Aus der Grafik ist zu erkennen: | |
| − | + | #Die zwei Codetabellen des Jessop–Waters–Codes sind so gewählt, dass die laufende digitale Summe ${\it \Sigma}_l$ stets zwischen $0$ und $5$ liegt.<br><br> | |
| − | + | #Bei den beiden anderen Codes (MS43, FoMoT) erreicht man durch drei bzw. vier alternative Tabellen die Beschränkung der laufenden digitalen Summe auf den Wertebereich $0 \le {\it \Sigma}_l \le 3$. | |
| − | Die zwei Codetabellen des Jessop–Waters–Codes sind so gewählt, dass die laufende digitale Summe stets zwischen $0$ und $5$ liegt. Bei den beiden anderen Codes (MS43, FoMoT) erreicht man durch drei bzw. vier alternative Tabellen die Beschränkung der laufenden digitalen Summe auf den Wertebereich $0 \le \ | ||
<br Clear = all> | <br Clear = all> | ||
| − | |||
| − | |||
== AKF und LDS der 4B3T–Codes== | == AKF und LDS der 4B3T–Codes== | ||
<br> | <br> | ||
| − | + | Die Vorgehensweise zur Berechnung von Autokorrelationsfunktion $\rm (AKF)$ und Leistungsdichtespektrum $\rm (LDS)$ wird hier nur stichpunktartig skizziert: | |
| − | Die Vorgehensweise | ||
| − | + | [[Datei:P_ID1335__Dig_T_2_3_S3_v1.png|right|frame|Markovdiagramm zur Analyse des 4B3T-FoMoT-Codes|class=fit]] | |
| − | + | '''(1)''' Der Übergang der laufenden digitalen Summe von ${\it \Sigma}_l$ nach ${\it \Sigma}_{l+1}$ wird durch eine homogene stationäre Markovkette erster Ordnung mit sechs (Jessop–Waters) bzw. vier Zuständen (MS43, FoMoT) beschrieben. Für den FoMoT–Code gilt das rechts skizzierte Markovdiagramm.<br> | |
| − | |||
| − | + | '''(2)''' Die Werte an den Pfeilen kennzeichnen die Übergangswahrscheinlichkeiten ${\rm Pr}({\it \Sigma}_{l+1}|{\it \Sigma}_{l})$, die sich aus den jeweiligen Codetabellen ergeben. Die Farben korrespondieren zu den Hinterlegungen der Tabelle auf der letzten Seite. Aufgrund der Symmetrie des FoMoT–Markovdiagramms sind die vier Wahrscheinlichkeiten alle gleich: | |
| + | :$${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}({\it \Sigma}_{l} = 3) = 1/4.$$ | ||
| + | '''(3)''' Die Autokorrelationsfunktion $\varphi_a(\lambda) = {\rm E}\big [a_\nu \cdot a_{\nu+\lambda}\big ]$ der Amplitudenkoeffizienten kann aus diesem Diagramm ermittelt werden. Einfacher als die analytische Berechnung, die eines sehr großen Rechenaufwands bedarf, ist die simulative Bestimmung der AKF–Werte mittels Computer.<br> | ||
| − | Durch Fouriertransformation der AKF kommt man zum Leistungsdichtespektrum (LDS) ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten | + | Durch Fouriertransformation der AKF kommt man zum Leistungsdichtespektrum (LDS) ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten gemäß der folgenden Grafik aus [ST85]<ref name ='ST85'>Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.</ref>. Das skizzierte LDS wurde für den FoMoT–Code ermittelt, dessen Markovdiagramm oben dargestellt ist. |
| − | |||
| − | Die | + | Die Unterschiede der einzelnen 4B3T–Codes sind nicht sonderlich ausgeprägt. So gilt |
| − | + | *für den MS43–Code ${\rm E}\big [a_\nu^2 \big ] \approx 0.65$ und | |
| + | *für die beiden anderen 4B3T-Codes (Jessop/Waters, MS43) ${\rm E}\big [a_\nu^2 \big ] \approx 0.69$. <br> | ||
| − | |||
| − | + | Die Aussagen dieser Grafik kann man wie folgt zusammenfassen: | |
| + | [[Datei:P_ID1336__Dig_T_2_3_S3b_v1.png|right|frame|Leistungsdichtespektrum (der Ampltudenkoeffizienten) von 4B3T im Vergleich zu redundanzfreier und AMI-Codierung|class=fit]] | ||
| − | *Die | + | *Die Grafik zeigt das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten $a_\nu$ des 4B3T-Codes ⇒ rote Kurve. |
| + | |||
| + | *Das LDS ${\it \Phi}_s(f)$ unter Einbeziehung des Sendegrundimpulses erhält man durch Multiplikation mit $1/T \cdot |G_s(f)|^2$. Beispielsweise muss man ${\it \Phi}_a(f)$ mit einer $\rm si^2$–Funktion multiplizieren, wenn $g_s(t)$ einen Rechteckimpuls beschreibt.<br> | ||
| − | * | + | *Bei redundanzfreier Binär– oder Ternärcodierung ergibt sich jeweils ein konstantes ${\it \Phi}_a(f)$, dessen Höhe von der Stufenzahl $M$ abhängt (unterschiedliche Signalleistung). |
| − | * | + | *Dagegen weist das 4B3T–Leistungsdichtespektrum Nullstellen bei $f = 0$ und Vielfachen von $f = 1/T$ auf.<br> |
| + | *Die Nullstelle bei $f = 0$ hat den Vorteil, dass das 4B3T–Signal ohne große Einbußen auch über einen so genannten "Telefonkanal" übertragen werden kann, der aufgrund von Übertragern für ein Gleichsignal nicht geeignet ist.<br> | ||
| − | = | + | *Die Nullstelle bei $f = 1/T$ hat den Nachteil, dass dadurch die Taktrückgewinnung am Empfänger erschwert wird. Außerhalb dieser Nullstellen weisen die 4B3T–Codes ein flacheres ${\it \Phi}_a(f)$ auf als der im nächsten Kapitel behandelte [[Digitalsignalübertragung/Symbolweise_Codierung_mit_Pseudoternärcodes#Eigenschaften_des_AMI-Codes|AMI–Code]] (blaue Kurve), was von Vorteil ist.<br> |
| − | |||
| − | |||
| − | |||
| − | *Der | + | *Der Grund für den flacheren LDS–Verlauf bei mittleren Frequenzen sowie für den steileren Abfall zu den Nullstellen hin ist, dass bei den 4B3T–Codes bis zu fünf $+1$–Koeffizienten (bzw. $-1$–Koeffizienten) aufeinanderfolgen können. Beim AMI–Code treten diese Symbole nur isoliert auf.<br> |
| − | |||
| − | |||
| − | + | == Fehlerwahrscheinlichkeit der 4B3T-Codes== | |
| + | <br> | ||
| + | Wir betrachten nun die Symbolfehlerwahrscheinlichkeit bei Verwendung des 4B3T–Codes im Vergleich zu redundanzfreier Binär– und Ternärcodierung, wobei folgende Voraussetzungen gelten sollen: | ||
| + | [[Datei:P_ID1338__Dig_T_2_3_S4_v2.png|right|frame|Augendiagramm bei redundanzfreier bzw. 4B3T-Codierung|class=fit]] | ||
| − | + | *Der Systemvergleich erfolgt zunächst unter der Nebenbedingung der „Spitzenwertbegrenzung”. Deshalb verwenden wir den rechteckförmigen Sendegrundimpuls, der hierfür optimal ist.<br> | |
| − | + | *Der Gesamtfrequenzgang zeigt einen Cosinus–Rolloff mit bestmöglichem Rolloff–Faktor $r = 0.8$. Die Rauschleistung $\sigma_d^2$ ist somit um $12\%$ größer als beim Matched-Filter (globales Optimum), siehe Grafik auf der Seite [[Digitalsignal%C3%BCbertragung/Optimierung_der_Basisband%C3%BCbertragungssysteme#Optimierung_des_Rolloff.E2.80.93Faktors_bei_Spitzenwertbegrenzung|"Optimierung des Rolloff-Faktors bei Spitzenwertbegrenzung"]] im dritten Hauptkapitel. | |
| − | |||
| − | |||
| − | + | Die Grafik zeigt die [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_unter_Berücksichtigung_von_Impulsinterferenzen#Definition_und_Aussagen_des_Augendiagramms|"Augendiagramme"]] (mit Rauschen) der drei zu vergleichenden Systeme und enthält zusätzlich $($in Zeile $\rm A)$ die Gleichungen zur Berechnung der Symbolfehlerwahrscheinlichkeit. Bei jedem Diagramm sind ca. 2000 Augenlinien gezeichnet. | |
| − | |||
| − | + | Die beiden ersten Zeilen beschreiben den Systemvergleich bei Spitzenwertbegrenzung. Für das Binärsystem ergibt sich die Rauschleistung (unter Berücksichtigung der $12\%$–Erhöhung) zu | |
| − | + | :$$\sigma_d^2 = 1.12 \cdot {N_0}/({2 \cdot T}) = 0.56 \cdot {N_0}/{T} = \sigma_1^2 \hspace{0.05cm}.$$ | |
| + | Für das verrauschte Augendiagramm und die folgenden Berechnungen ist jeweils der „Störabstand” $10 \cdot \lg \hspace{0.05cm}(s_0^2 \cdot T/N_0) = 13 \ \rm dB$ zugrunde gelegt. Damit erhält man: | ||
| + | :$$10 \cdot {\rm lg } \hspace{0.1cm}{s_0^2 \cdot T}/{N_0} = 13 \, {\rm dB } \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}{s_0^2 \cdot T}/{N_0} = 10^{1.3} \approx 20 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}\sigma_1^2 = 0.56 \cdot {s_0^2}/{20} \approx 0.028 \cdot s_0^2 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}{ \sigma_1}/{s_0}\approx 0.167 \hspace{0.05cm}.$$ | ||
| − | + | In der Zeile $\rm B$ ist die dazugehörige Symbolfehlerwahrscheinlichkeit | |
| − | + | $p_{\rm S} \approx {\rm Q}(s_0/\sigma_1) \approx {\rm Q}(6) = 10^{-9}$ angegeben. | |
| − | |||
Die beiden weiteren Augendiagramme lassen sich wie folgt interpretieren: | Die beiden weiteren Augendiagramme lassen sich wie folgt interpretieren: | ||
| − | *Beim redundanzfreien Ternärsystem ist die Augenöffnung nur halb so groß wie beim Binärsystem und die Rauschleistung | + | *Beim redundanzfreien Ternärsystem ist die Augenöffnung nur halb so groß wie beim Binärsystem und die Rauschleistung $\sigma_2^2$ ist um den Faktor $\log_2 \hspace{0.05cm}(3)$ kleiner als $\sigma_1^2$. Der Faktor $4/3$ vor der Q–Funktion berücksichtigt, dass die ternäre „0” in beiden Richtungen verfälscht werden kann. Damit ergeben sich folgende Zahlenwerte: |
| − | + | :$$\frac{ \sigma_2}{s_0}\hspace{-0.05cm} =\hspace{-0.05cm} \frac{ \sigma_1/s_0}{\sqrt{{\rm log_2} (3)}}\hspace{-0.05cm} =\hspace{-0.05cm}\frac{ 0.167}{1.259} | |
| − | + | \approx 0.133 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm S}\hspace{-0.05cm}=\hspace{-0.05cm} {4}/{3} \cdot {\rm Q}\left (\frac{ 0.5}{0.133}\right)\approx | |
| + | {4}/{3} \cdot {\rm Q}(3.76) \hspace{-0.05cm}= \hspace{-0.05cm}1.1 \cdot 10^{-4} .$$ | ||
| + | *Der 4B3T–Code liefert noch etwas ungünstigere Ergebnisse, da hier bei gleicher Augenöffnung die Rauschleistung $(\sigma_3^2)$ weniger stark vermindert wird als beim redundanzfreien Ternärcode $(\sigma_2^2)$: | ||
| + | :$$\frac{ \sigma_3}{s_0} = \frac{ \sigma_1/s_0}{\sqrt{4/3}} =\frac{ 0.167}{1.155} | ||
| + | \approx 0.145 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm S}= {4}/{3} \cdot {\rm Q}\left (\frac{ 0.5}{0.145}\right)\approx | ||
| + | {4}/{3} \cdot {\rm Q}(3.45) = 3.7 \cdot 10^{-4} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | $\text{Zeile C: Symbolfehlerwahrscheinlichkeiten bei Leistungsbegrenzung}$ | |
| − | + | ⇒ Dabei ist der rechteckförmigige Sendegrundimpuls $g_{s}(t)$ und $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) = 13 \ \rm dB$ vorgegeben: | |
| − | \ | + | |
| − | + | *Beim '''redundanzfreien Binärsystem''' mit NRZ–Rechteckimpulsen wird $p_{\rm S}$ gegenüber der Zeile $\rm B$ wegen $E_{\rm B} = s_0^2 \cdot T$ nicht verändert: | |
| + | :$$p_\text{S, Leistungsbegrenzung} = p_\text{S, Spitzenwertbegrenzung} \approx 10^{-9}.$$ | ||
| + | *Für die beiden Ternärcodes gilt ${\rm E}\big [a_\nu^2\big ] \approx 2/3$. Deshalb kann hier die Amplitude um den Faktor $\sqrt{(3/2)} \approx 1.225$ vergrößert werden. | ||
| − | * | + | * Für den '''redundanzfreien Ternärcode''' erhält man damit bei Leistungsbegrenzung eine um mehr als den Faktor $4$ kleinere Fehlerwahrscheinlichkeit als bei Spitzenwertbegrenzung (vgl. die Zeilen $\rm B$ und $\rm C$ in obiger Tabelle): |
| + | :$$p_\text{S, Leistungsbegrenzung} = 4/3 \cdot {\rm Q}(1.225 \cdot 3.76) \approx 2.9 \cdot 10^{-5} \approx 0.26 \cdot p_\text{S, Spitzenwertbegrenzung} .$$ | ||
| + | *Ähnliches (und sogar noch verstärkt) gilt auch für den 4B3T-Code: | ||
| + | :$$p_\text{S, Leistungsbegrenzung} = 4/3 \cdot {\rm Q}(1.225 \cdot 3.45) \approx 1.5 \cdot 10^{-5} \approx 0.04 \cdot p_\text{S, Spitzenwertbegrenzung}.$$ | ||
| − | |||
| − | ==Aufgaben== | + | ==Aufgaben zum Kapitel== |
<br> | <br> | ||
| − | [[Aufgaben:2.6 Modifizierter MS43-Code| | + | [[Aufgaben:2.6 Modifizierter MS43-Code|Aufgabe 2.6: Modifizierter MS43-Code]] |
| − | [[ | + | [[Aufgaben:2.6Z_4B3T-Code_nach_Jessop_und_Waters|Aufgabe 2.6Z: 4B3T-Code nach Jessop und Waters]] |
==Quellenverzeichnis== | ==Quellenverzeichnis== | ||
Aktuelle Version vom 18. Mai 2022, 15:13 Uhr
Inhaltsverzeichnis
Allgemeine Beschreibung von Blockcodes
Bei Blockcodierung wird jeweils eine Sequenz von $m_q$ binären Quellensymbolen $(M_q = 2)$ durch einen Block von $m_c$ Codesymbolen mit dem Symbolumfang $M_c$ dargestellt. Um eine jede Quellensymbolfolge $\langle q_\nu \rangle$ in eine Codesymbolfolge $\langle c_\nu \rangle$ umsetzen zu können, muss folgende Bedingung erfüllt sein:
- $$M_c^{\hspace{0.1cm}m_c} \ge M_q^{\hspace{0.1cm}m_q}\hspace{0.05cm}.$$
- Bei den im letzten Kapitel behandelten redundanzfreien Codes gilt in dieser Gleichung das Gleichheitszeichen, wenn $M_q$ eine Zweierpotenz ist.
- Mit dem Größerzeichen ergibt sich ein redundantes Digitalsignal, wobei die relative Coderedundanz wie folgt berechnet werden kann:
- $$r_c = 1- \frac{m_q \cdot {\rm log_2}\hspace{0.05cm} (M_q)}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)} > 0 \hspace{0.05cm}.$$
Der bekannteste Blockcode zur Übertragungscodierung ist der 4B3T–Code mit den Codeparametern
- $$m_q = 4,\hspace{0.2cm}M_q = 2,\hspace{0.2cm}m_c = 3,\hspace{0.2cm}M_c = 3\hspace{0.05cm},$$
der bereits in den 1970–er Jahren entwickelt wurde und beispielsweise bei ISDN ("Integrated Services Digital Networks") eingesetzt wird.
Ein 4B3T–Code besitzt folgende Eigenschaften:
- Wegen $m_q \cdot T_{\rm B} = m_c \cdot T$ ist die Symboldauer $T$ des Codersignals um den Faktor $4/3$ größer als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Daraus ergibt sich die günstige Eigenschaft, dass der Bandbreitenbedarf um ein Viertel geringer ist als bei redundanzfreier Binärübertragung.
- Die relative Redundanz kann mit obiger Gleichung berechnet werden und ergibt sich zu $r_c \approx 16\%$. Diese Redundanz wird beim 4B3T–Code dazu verwendet, um Gleichsignalfreiheit zu erzielen.
- Das 4B3T–codierte Signal kann somit ohne merkbare Beeinträchtigung auch über einen Kanal mit der Eigenschaft $H_{\rm K}(f)= 0) = 0$ übertragen werden.
Die Umcodierung der sechzehn möglichen Binärblöcke in die entsprechenden Ternärblöcke könnte prinzipiell nach einer festen Codetabelle vorgenommen werden. Um die spektralen Eigenschaften dieser Codes weiter zu verbessern, werden bei den gebräuchlichen 4B3T–Codes, nämlich
- dem 4B3T–Code nach Jessop und Waters,
- dem MS43–Code (von: $\rm M$onitored $\rm S$um $\rm 4$B$\rm 3$T–Code),
- dem FoMoT–Code (von: $\rm Fo$ur $\rm Mo$de $\rm T$ernary),
zwei oder mehrere Codetabellen verwendet, deren Auswahl von der "laufenden digitalen Summe" der Amplitudenkoeffizienten gesteuert wird.
Das Prinzip wird auf der nächsten Seite erklärt.
Laufende digitale Summe
Nach der Übertragung von $l$ codierten Blöcken gilt für die "laufende digitale Summe" mit den ternären Amplitudenkoeffizienten $a_\nu \in \{ -1, 0, +1\}$:
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}.$$
Die Auswahl der Tabelle zur Codierung des $(l + 1)$–ten Blocks erfolgt abhängig vom aktuellen Wert ${\it \Sigma}_l$.
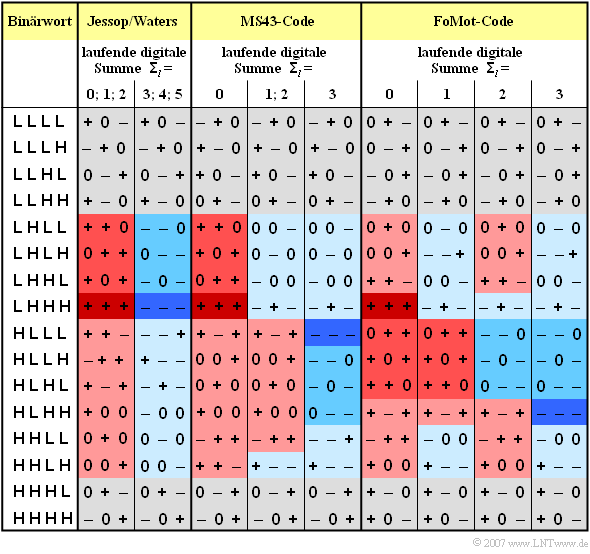
In der Tabelle sind die Codierregeln für die drei oben genannten 4B3T–Codes angegeben. Zur Vereinfachung der Schreibweise steht
- „+” für den Amplitudenkoeffizienten „+1” und
- „–” für den Koeffizienten „–1”.
Aus der Grafik ist zu erkennen:
- Die zwei Codetabellen des Jessop–Waters–Codes sind so gewählt, dass die laufende digitale Summe ${\it \Sigma}_l$ stets zwischen $0$ und $5$ liegt.
- Bei den beiden anderen Codes (MS43, FoMoT) erreicht man durch drei bzw. vier alternative Tabellen die Beschränkung der laufenden digitalen Summe auf den Wertebereich $0 \le {\it \Sigma}_l \le 3$.
AKF und LDS der 4B3T–Codes
Die Vorgehensweise zur Berechnung von Autokorrelationsfunktion $\rm (AKF)$ und Leistungsdichtespektrum $\rm (LDS)$ wird hier nur stichpunktartig skizziert:
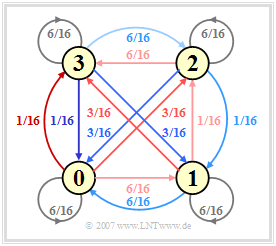
(1) Der Übergang der laufenden digitalen Summe von ${\it \Sigma}_l$ nach ${\it \Sigma}_{l+1}$ wird durch eine homogene stationäre Markovkette erster Ordnung mit sechs (Jessop–Waters) bzw. vier Zuständen (MS43, FoMoT) beschrieben. Für den FoMoT–Code gilt das rechts skizzierte Markovdiagramm.
(2) Die Werte an den Pfeilen kennzeichnen die Übergangswahrscheinlichkeiten ${\rm Pr}({\it \Sigma}_{l+1}|{\it \Sigma}_{l})$, die sich aus den jeweiligen Codetabellen ergeben. Die Farben korrespondieren zu den Hinterlegungen der Tabelle auf der letzten Seite. Aufgrund der Symmetrie des FoMoT–Markovdiagramms sind die vier Wahrscheinlichkeiten alle gleich:
- $${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}({\it \Sigma}_{l} = 3) = 1/4.$$
(3) Die Autokorrelationsfunktion $\varphi_a(\lambda) = {\rm E}\big [a_\nu \cdot a_{\nu+\lambda}\big ]$ der Amplitudenkoeffizienten kann aus diesem Diagramm ermittelt werden. Einfacher als die analytische Berechnung, die eines sehr großen Rechenaufwands bedarf, ist die simulative Bestimmung der AKF–Werte mittels Computer.
Durch Fouriertransformation der AKF kommt man zum Leistungsdichtespektrum (LDS) ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten gemäß der folgenden Grafik aus [ST85][1]. Das skizzierte LDS wurde für den FoMoT–Code ermittelt, dessen Markovdiagramm oben dargestellt ist.
Die Unterschiede der einzelnen 4B3T–Codes sind nicht sonderlich ausgeprägt. So gilt
- für den MS43–Code ${\rm E}\big [a_\nu^2 \big ] \approx 0.65$ und
- für die beiden anderen 4B3T-Codes (Jessop/Waters, MS43) ${\rm E}\big [a_\nu^2 \big ] \approx 0.69$.
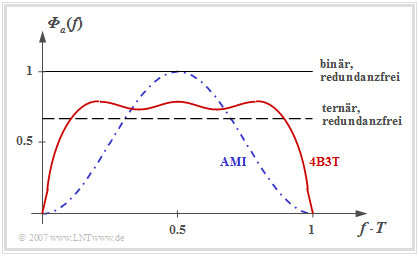
Die Aussagen dieser Grafik kann man wie folgt zusammenfassen:
- Die Grafik zeigt das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten $a_\nu$ des 4B3T-Codes ⇒ rote Kurve.
- Das LDS ${\it \Phi}_s(f)$ unter Einbeziehung des Sendegrundimpulses erhält man durch Multiplikation mit $1/T \cdot |G_s(f)|^2$. Beispielsweise muss man ${\it \Phi}_a(f)$ mit einer $\rm si^2$–Funktion multiplizieren, wenn $g_s(t)$ einen Rechteckimpuls beschreibt.
- Bei redundanzfreier Binär– oder Ternärcodierung ergibt sich jeweils ein konstantes ${\it \Phi}_a(f)$, dessen Höhe von der Stufenzahl $M$ abhängt (unterschiedliche Signalleistung).
- Dagegen weist das 4B3T–Leistungsdichtespektrum Nullstellen bei $f = 0$ und Vielfachen von $f = 1/T$ auf.
- Die Nullstelle bei $f = 0$ hat den Vorteil, dass das 4B3T–Signal ohne große Einbußen auch über einen so genannten "Telefonkanal" übertragen werden kann, der aufgrund von Übertragern für ein Gleichsignal nicht geeignet ist.
- Die Nullstelle bei $f = 1/T$ hat den Nachteil, dass dadurch die Taktrückgewinnung am Empfänger erschwert wird. Außerhalb dieser Nullstellen weisen die 4B3T–Codes ein flacheres ${\it \Phi}_a(f)$ auf als der im nächsten Kapitel behandelte AMI–Code (blaue Kurve), was von Vorteil ist.
- Der Grund für den flacheren LDS–Verlauf bei mittleren Frequenzen sowie für den steileren Abfall zu den Nullstellen hin ist, dass bei den 4B3T–Codes bis zu fünf $+1$–Koeffizienten (bzw. $-1$–Koeffizienten) aufeinanderfolgen können. Beim AMI–Code treten diese Symbole nur isoliert auf.
Fehlerwahrscheinlichkeit der 4B3T-Codes
Wir betrachten nun die Symbolfehlerwahrscheinlichkeit bei Verwendung des 4B3T–Codes im Vergleich zu redundanzfreier Binär– und Ternärcodierung, wobei folgende Voraussetzungen gelten sollen:
- Der Systemvergleich erfolgt zunächst unter der Nebenbedingung der „Spitzenwertbegrenzung”. Deshalb verwenden wir den rechteckförmigen Sendegrundimpuls, der hierfür optimal ist.
- Der Gesamtfrequenzgang zeigt einen Cosinus–Rolloff mit bestmöglichem Rolloff–Faktor $r = 0.8$. Die Rauschleistung $\sigma_d^2$ ist somit um $12\%$ größer als beim Matched-Filter (globales Optimum), siehe Grafik auf der Seite "Optimierung des Rolloff-Faktors bei Spitzenwertbegrenzung" im dritten Hauptkapitel.
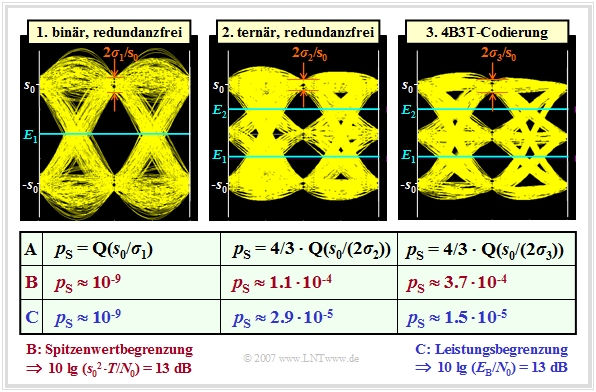
Die Grafik zeigt die "Augendiagramme" (mit Rauschen) der drei zu vergleichenden Systeme und enthält zusätzlich $($in Zeile $\rm A)$ die Gleichungen zur Berechnung der Symbolfehlerwahrscheinlichkeit. Bei jedem Diagramm sind ca. 2000 Augenlinien gezeichnet.
Die beiden ersten Zeilen beschreiben den Systemvergleich bei Spitzenwertbegrenzung. Für das Binärsystem ergibt sich die Rauschleistung (unter Berücksichtigung der $12\%$–Erhöhung) zu
- $$\sigma_d^2 = 1.12 \cdot {N_0}/({2 \cdot T}) = 0.56 \cdot {N_0}/{T} = \sigma_1^2 \hspace{0.05cm}.$$
Für das verrauschte Augendiagramm und die folgenden Berechnungen ist jeweils der „Störabstand” $10 \cdot \lg \hspace{0.05cm}(s_0^2 \cdot T/N_0) = 13 \ \rm dB$ zugrunde gelegt. Damit erhält man:
- $$10 \cdot {\rm lg } \hspace{0.1cm}{s_0^2 \cdot T}/{N_0} = 13 \, {\rm dB } \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{s_0^2 \cdot T}/{N_0} = 10^{1.3} \approx 20 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\sigma_1^2 = 0.56 \cdot {s_0^2}/{20} \approx 0.028 \cdot s_0^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \sigma_1}/{s_0}\approx 0.167 \hspace{0.05cm}.$$
In der Zeile $\rm B$ ist die dazugehörige Symbolfehlerwahrscheinlichkeit $p_{\rm S} \approx {\rm Q}(s_0/\sigma_1) \approx {\rm Q}(6) = 10^{-9}$ angegeben.
Die beiden weiteren Augendiagramme lassen sich wie folgt interpretieren:
- Beim redundanzfreien Ternärsystem ist die Augenöffnung nur halb so groß wie beim Binärsystem und die Rauschleistung $\sigma_2^2$ ist um den Faktor $\log_2 \hspace{0.05cm}(3)$ kleiner als $\sigma_1^2$. Der Faktor $4/3$ vor der Q–Funktion berücksichtigt, dass die ternäre „0” in beiden Richtungen verfälscht werden kann. Damit ergeben sich folgende Zahlenwerte:
- $$\frac{ \sigma_2}{s_0}\hspace{-0.05cm} =\hspace{-0.05cm} \frac{ \sigma_1/s_0}{\sqrt{{\rm log_2} (3)}}\hspace{-0.05cm} =\hspace{-0.05cm}\frac{ 0.167}{1.259} \approx 0.133 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm S}\hspace{-0.05cm}=\hspace{-0.05cm} {4}/{3} \cdot {\rm Q}\left (\frac{ 0.5}{0.133}\right)\approx {4}/{3} \cdot {\rm Q}(3.76) \hspace{-0.05cm}= \hspace{-0.05cm}1.1 \cdot 10^{-4} .$$
- Der 4B3T–Code liefert noch etwas ungünstigere Ergebnisse, da hier bei gleicher Augenöffnung die Rauschleistung $(\sigma_3^2)$ weniger stark vermindert wird als beim redundanzfreien Ternärcode $(\sigma_2^2)$:
- $$\frac{ \sigma_3}{s_0} = \frac{ \sigma_1/s_0}{\sqrt{4/3}} =\frac{ 0.167}{1.155} \approx 0.145 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm S}= {4}/{3} \cdot {\rm Q}\left (\frac{ 0.5}{0.145}\right)\approx {4}/{3} \cdot {\rm Q}(3.45) = 3.7 \cdot 10^{-4} \hspace{0.05cm}.$$
$\text{Zeile C: Symbolfehlerwahrscheinlichkeiten bei Leistungsbegrenzung}$
⇒ Dabei ist der rechteckförmigige Sendegrundimpuls $g_{s}(t)$ und $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) = 13 \ \rm dB$ vorgegeben:
- Beim redundanzfreien Binärsystem mit NRZ–Rechteckimpulsen wird $p_{\rm S}$ gegenüber der Zeile $\rm B$ wegen $E_{\rm B} = s_0^2 \cdot T$ nicht verändert:
- $$p_\text{S, Leistungsbegrenzung} = p_\text{S, Spitzenwertbegrenzung} \approx 10^{-9}.$$
- Für die beiden Ternärcodes gilt ${\rm E}\big [a_\nu^2\big ] \approx 2/3$. Deshalb kann hier die Amplitude um den Faktor $\sqrt{(3/2)} \approx 1.225$ vergrößert werden.
- Für den redundanzfreien Ternärcode erhält man damit bei Leistungsbegrenzung eine um mehr als den Faktor $4$ kleinere Fehlerwahrscheinlichkeit als bei Spitzenwertbegrenzung (vgl. die Zeilen $\rm B$ und $\rm C$ in obiger Tabelle):
- $$p_\text{S, Leistungsbegrenzung} = 4/3 \cdot {\rm Q}(1.225 \cdot 3.76) \approx 2.9 \cdot 10^{-5} \approx 0.26 \cdot p_\text{S, Spitzenwertbegrenzung} .$$
- Ähnliches (und sogar noch verstärkt) gilt auch für den 4B3T-Code:
- $$p_\text{S, Leistungsbegrenzung} = 4/3 \cdot {\rm Q}(1.225 \cdot 3.45) \approx 1.5 \cdot 10^{-5} \approx 0.04 \cdot p_\text{S, Spitzenwertbegrenzung}.$$
Aufgaben zum Kapitel
Aufgabe 2.6: Modifizierter MS43-Code
Aufgabe 2.6Z: 4B3T-Code nach Jessop und Waters
Quellenverzeichnis
- ↑ Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.