Signaldarstellung/Faltungssatz und Faltungsoperation: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (39 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
==Faltung im Zeitbereich== | ==Faltung im Zeitbereich== | ||
| + | <br> | ||
| + | Der „Faltungssatz” ist mit das wichtigste Gesetz der Fouriertransformation, dem in vorliegendem Tutorial ein eigenes Unterkapitel gewidmet wird. | ||
| − | + | Wir betrachten zunächst den Faltungssatz im Zeitbereich und setzen voraus, dass die Spektren zweier Zeitfunktionen $x_1(t)$ und $x_2(t)$ bekannt sind: | |
| − | |||
| − | $$X_1 ( f )\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\ | + | :$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ |
| − | Dann gilt für die Zeitfunktion des Produktes $X_1(f) \cdot X_2(f)$: | + | Dann gilt für die Zeitfunktion des Produktes $X_1(f) \cdot X_2(f)$: |
| − | $$X_1 ( f ) \cdot X_2 ( f )\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\ | + | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ |
| − | Hierbei ist $\tau$ eine formale Integrationsvariable mit der Dimension einer Zeit. | + | Hierbei ist $\tau$ eine formale Integrationsvariable mit der Dimension einer Zeit. |
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | Die obige Verknüpfung der Zeitfunktion | + | $\text{Definition:}$ Die obige Verknüpfung der Zeitfunktion $x_1(t)$ und $x_2(t)$ bezeichnet man als $\text{Faltung}$ und stellt diesen Funktionalzusammenhang mit einem Stern dar: |
| − | $$x_{\rm{1}} (t) * x_{\rm{2}} (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2}} (t) * x_{\rm{1}} (t) .$$ | + | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$ |
| − | Damit lässt sich obige Fourierkorrespondenz auch wie folgt schreiben: | + | *Damit lässt sich obige Fourierkorrespondenz auch wie folgt schreiben: |
| − | $$X_1 ( f ) \cdot X_2 ( f )\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\ | + | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ |
| − | ⇒ | + | *Die Faltung ist $\text{"kommutativ"}$ ⇒ Die Reihenfolge der Operanden ist vertauschbar: |
| + | :$$x_1(t) * x_2(t) =x_2(t) * x_1(t).$$ | ||
| + | *Der [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Beweis_des_Faltungssatzes|Beweis]] folgt am Kapitelende.}} | ||
| − | |||
| + | [[Datei:P_ID579__Sig_T_3_4_S1_neu.png|right|frame|Zur Berechnung von Signal und Spektrum am LZI–Ausgang]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Ein jedes lineare zeitinvariante (LZI-) System kann sowohl durch den Frequenzgang $H(f)$ als auch durch die Impulsantwort $h(t)$ beschrieben werden, wobei der Zusammenhang zwischen diesen beiden Systemgrößen ebenfalls durch die Fouriertransformation gegeben ist. | ||
| − | + | Legt man an den Eingang ein Signal $x(t)$ mit dem Spektrum $X(f)$ an, so gilt für das Spektrum des Ausgangssignals: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Legt man an den Eingang ein Signal $x(t)$ mit dem Spektrum $X(f)$ an, so gilt für das Spektrum des Ausgangssignals: | ||
| − | $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | + | :$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ |
| − | Mit dem Faltungssatz ist es | + | Mit dem Faltungssatz ist es möglich, das Ausgangssignal auch direkt im Zeitbereich zu berechnen: |
| − | $$y( t ) | + | :$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ |
| − | Aus dieser Gleichung geht nochmals hervor, dass die Faltungsoperation | + | Aus dieser Gleichung geht nochmals hervor, dass die Faltungsoperation „kommutativ” ist.}} |
| − | |||
| − | |||
==Faltung im Frequenzbereich== | ==Faltung im Frequenzbereich== | ||
| − | + | <br> | |
| − | Die Dualität zwischen | + | Die Dualität zwischen Zeit– und Frequenzbereich erlaubt auch Aussagen hinsichtlich des Spektrums des Produktsignals: |
| − | $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | + | :$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ |
| − | Dieses Resultat lässt sich ähnlich wie der Faltungssatz im Zeitbereich beweisen. | + | Dieses Resultat lässt sich ähnlich wie der [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Beweis_des_Faltungssatzes|Faltungssatz im Zeitbereich]] beweisen. Die Integrationsvariable $\nu$ hat aber nun die Dimension einer Frequenz. |
| − | {{Beispiel} | + | [[Datei:P_ID580__Sig_T_3_4_S2_neu.png|right|frame|Faltung im Frequenzbereich am Beispiel der ZSB–AM]] |
| − | Die Zweiseitenband-Amplitudenmodulation (ZSB-AM) ohne Träger wird durch das | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 2:}$ Die [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#Beschreibung_im_Zeitbereich|Zweiseitenband-Amplitudenmodulation]] (ZSB-AM) ohne Träger wird durch das skizzierte Modell beschrieben. | ||
| + | *Bei der Zeitbereichsdarstellung (blau) ergibt sich das modulierte Signal $s(t)$ als das Produkt aus dem Nachrichtensignal $q(t)$ und dem (normierten) Trägersignal $z(t)$. | ||
| − | |||
| − | + | *Nach dem Faltungssatz folgt daraus für den Frequenzbereich (rot), dass das Ausgangsspektrum $S(f)$ gleich dem Faltungsprodukt aus $Q(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ q(t)$ und $Z(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ z(t)$ ist.}} | |
==Faltung einer Funktion mit einer Diracfunktion== | ==Faltung einer Funktion mit einer Diracfunktion== | ||
| + | <br> | ||
| + | Sehr einfach wird die Faltungsoperation, wenn einer der beiden Operanden eine [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktion]] ist. Dies gilt für die Faltung im Zeit– und im Frequenzbereich gleichermaßen. | ||
| − | + | *Wir betrachten beispielhaft die Faltung einer Funktion $x_1(t)$ mit der Funktion | |
| − | Wir betrachten beispielhaft die Faltung einer Funktion $x_1(t)$ mit der Funktion | ||
| − | $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }} | + | :$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ |
| − | Für die Spektralfunktion des Signals $y(t) = x_1(t) \ast x_2(t)$ gilt dann: | + | *Für die Spektralfunktion des Signals $y(t) = x_1(t) \ast x_2(t)$ gilt dann: |
| − | $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }} | + | :$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ |
| + | |||
| + | *Die komplexe Exponentialfunktion führt zur Verschiebung um $T$ ⇒ [[Signaldarstellung/Gesetzm%C3%A4%C3%9Figkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz]], der Faktor $\alpha$ zu einer Dämpfung $(\alpha < 1)$ bzw. Verstärkung $(\alpha > 1)$. | ||
| − | + | *Daraus folgt: | |
| − | $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | + | :$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{In Worten: }$ Die Faltung einer beliebigen Funktion mit einer Diracfunktion bei $t = T$ ergibt die um $T$ nach rechts verschobene Funktion, wobei noch die Gewichtung der Diracfunktion durch den Faktor $\alpha$ zu berücksichtigen ist.}} | ||
| − | |||
| − | {{Beispiel} | + | [[Datei:P_ID522__Sig_T_3_4_S3_neu.png|right|frame|Faltung eines Rechtecks mit einer Diracfunktion]] |
| − | Ein Rechtecksignal $x(t)$ wird durch ein LZI-System | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 3:}$ Ein Rechtecksignal $x(t)$ wird durch ein LZI-System um die Laufzeit $\tau = 3\,\text{ ms}$ verzögert und um den Faktor $\alpha = 0.5$ gedämpft. | ||
| − | |||
| − | + | Verschiebung und Dämpfung erkennt man sowohl | |
| + | *am Ausgangssignal $y(t)$ | ||
| + | *als auch an der Impulsantwort $h(t)$.}} | ||
==Grafische Faltung== | ==Grafische Faltung== | ||
| + | <br> | ||
| + | [[Datei:P_ID2723__Sig_T_3_4_programm.png|right|frame|Bildschirmabzug des Programms „Faltung” in einer früheren Version:<br> $x_1(t)$ ist hier mit $x(t)$ bezeichnet und $x_2(t)$ mit $h(t)$ ]] | ||
| + | Für die Beschreibungen auf dieser Seite wird von folgender Faltungsoperation ausgegangen: | ||
| − | + | :$$y(t) = x_1 (t) * x_2 (t) $$ | |
| − | + | :$$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | |
| − | $$y(t) = x_1 (t) * x_2 (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | + | |
| + | Die Lösung des Faltungsintegrals soll auf grafischem Wege erfolgen Es wird hier vorausgesetzt, dass $x_1(t)$ und $x_2(t)$ zeitkontinuierliche Signale sind. | ||
| − | + | Dann sind die folgenden Schritte erforderlich: | |
| − | #Die Zeitvariablen der beiden Funktionen ändern: $x_1(t) \to x_1(\tau)$,$x_2(t) \to x_2(\tau)$. | + | # Die '''Zeitvariablen''' der beiden Funktionen '''ändern''': <br> $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. |
| − | #Zweite Funktion spiegeln: $x_2(\tau) \to x_2(-\tau)$. | + | # Zweite '''Funktion spiegeln''': $x_2(\tau) \to x_2(-\tau)$. |
| − | #Gespiegelte Funktion um t verschieben: $x_2(-\tau) \to x_2(t-\tau)$. | + | # Gespiegelte '''Funktion''' um $t$ '''verschieben''': $x_2(-\tau) \to x_2(t-\tau)$. |
| − | #Multiplikation der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$. | + | # '''Multiplikation''' der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$. |
| − | #Integration über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$. | + | # '''Integration''' über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$. |
| − | |||
| − | |||
| − | |||
| + | Da die Faltung kommutativ ist, kann statt $x_2(\tau)$ auch $x_1(\tau)$ gespiegelt werden. | ||
| + | <br><br> | ||
| − | {{Beispiel} | + | Die Thematik wird auch durch das (neuere) HTML 5–Applet [[Applets:Zur_Verdeutlichung_der_grafischen_Faltung|Zur Verdeutlichung der grafischen Faltung]] veranschaulicht. |
| − | Am Eingang eines | + | <br clear=all> |
| − | + | [[Datei:P_ID582__Sig_T_3_4_S4_neu.png|right|frame|Beispiel einer Faltungsoperation: <br>Sprungfunktion gefaltet mit Exponentialfunktion]] | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 4:}$ | ||
| + | Die Vorgehensweise bei der grafischen Faltung wird nun anhand eines ausführlichen Beispiels erklärt: | ||
| + | *Am Eingang eines Filters liege eine Sprungfunktion $x(t) = \gamma(t)$ an. | ||
| + | *Die Impulsantwort des RC-Tiefpasses sei $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$ | ||
| + | *Die Zeitachse ist bereits in $\tau$ umbenannt. | ||
| − | |||
| − | |||
| − | $x(\tau)$ | + | Die Grafik zeigt |
| − | $h(\tau)$ | + | *rot das Eingangssignal $x(\tau)$, |
| − | $y(\tau)$ | + | *blau die Impulsantwort $h(\tau)$, |
| + | *grau das Ausgangssignal $y(\tau)$. | ||
| − | Das Ausgangssignal | + | Das Ausgangssignal kann zum Beispiel nach folgender Gleichung berechnet werden: |
| − | $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | + | :$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ |
Noch einige Anmerkungen zur grafischen Faltung: | Noch einige Anmerkungen zur grafischen Faltung: | ||
| − | *Der Ausgangswert bei $t | + | *Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal $x(\tau)$ spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert. |
| − | *Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich | + | *Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich Null ist, folgt daraus $y(t=0)=0$. |
| − | *Für jeden anderen Zeitpunkt t muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$. | + | *Für jeden anderen Zeitpunkt $t$ muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$. |
| − | |||
| − | |||
| − | |||
| − | + | Da im Beispiel auch $x(t-\tau)$ nur $0$ und $1$ sein kann, wird die Integration $($allgemein von $\tau_1$ bis $\tau_2)$ sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$ : | |
| + | :$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | ||
| − | { | + | Die Skizze gilt für $t=T$ und führt zum Ausgangswert $y(t=T) = 1 - 1/\text{e} \approx 0.632$.}} |
==Anschauliche Deutung der Faltung== | ==Anschauliche Deutung der Faltung== | ||
| + | <br> | ||
| + | Wir gehen von einer Impulsantwort $h(t)$ aus, die zunächst eine Millisekunde lang konstant ist und dann bis zur Zeit $t = 3 \,\text{ms}$ linear auf Null abfällt. | ||
| + | *Legt man an den Eingang dieses Tiefpassfilters einen Diracimpuls $K_0 \cdot \delta(t)$ an, so ist das Ausgangssignal $y(t)$ formgleich mit der Impulsantwort $h(t)$. Der Sachverhalt ist im Bild rot dargestellt. | ||
| + | *Ein um $T= 1 \,\text{ms}$ späterer Diracimpuls mit Gewicht $K_1 > K_0$ hat das blau gezeichnete Ausgangssignal $y_1(t)$ zur Folge, das gegenüber dem roten Signal verzögert und in der Amplitude vergrößert ist. | ||
| − | Wir betrachten | + | [[Datei:P_ID524__Sig_T_3_4_S5_rah.png|right|frame|Zur anschaulichen Deutung der Faltung]] |
| − | + | <br><br>Wir betrachten nun das aus sieben verschieden gewichteten und verschobenen Diracimpulsen bestehende Eingangssignal | |
| + | |||
| + | :$$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$ | ||
| − | + | das als zeitdiskrete Näherung eines zeitkontinuierlichen Signals aufgefasst werden kann. | |
| − | |||
| − | |||
| − | + | Das Signal am Ausgang des linearen Systems ist die Summe der sieben im Bild verschiedenfarbig markierten Teilsignale: | |
| − | $$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$ | + | :$$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$ |
| − | + | Wir betrachten nun den Signalwert zur Zeit $t = 4.5T$ (siehe Strichpunktierung): | |
| − | $$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$ | + | :$$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$ |
| − | + | Dieser Signalwert wird somit nur durch die Eingangssignalwerte $K_2$, $K_3$ und $K_4$ bestimmt. Der Einfluss | |
| − | *von $K_4$ wegen $h(0.5T) = 1$ am stärksten, | + | *von $K_4$ ist wegen $h(0.5T) = 1$ am stärksten, |
| − | *von $K_3$ wegen $h(1.5T) = 0.75$ weniger stark, | + | *von $K_3$ ist wegen $h(1.5T) = 0.75$ weniger stark, |
| − | *von $K_2$ wegen $h(2.5T) = 0.25$ am geringsten. | + | *von $K_2$ ist wegen $h(2.5T) = 0.25$ am geringsten. |
==Beweis des Faltungssatzes== | ==Beweis des Faltungssatzes== | ||
| − | + | <br> | |
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | Man | + | $\text{Definition: }$ |
| + | Man nennt die folgende Verknüpfung der Zeitfunktionen $x_1(t)$ und $x_2(t)$ die $\text{Faltung}$ und stellt diesen Funktionalzusammenhang mit einem Stern dar: | ||
| − | $$x_{\rm{1}} (t) * x_{\rm{2}} (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | + | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ |
Daraus ergibt sich die folgende Fourierkorrespondenz: | Daraus ergibt sich die folgende Fourierkorrespondenz: | ||
| − | $$X_1 ( f ) \cdot X_2 ( f )\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\ | + | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$}} |
| − | |||
| − | |||
| − | Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen: | + | {{BlaueBox|TEXT= |
| + | $\text{Beweis: }$ | ||
| + | Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen: | ||
| − | $$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}f\tau }\hspace{0.1cm} {\rm{d }}\tau{\rm{,}}$$ | + | :$$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$ |
| − | $$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} )} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}ft'}\hspace{0.1cm} {\rm{d}}t'{\rm{.}}$$ | + | :$$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t{0.05cm}'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$ |
| − | Bildet man das Produkt der Spektralfunktionen, so erhält man: | + | *Bildet man das Produkt der Spektralfunktionen, so erhält man: |
| − | $$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t'} ) \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}f\left( {\tau + t'} \right)}\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t'{\rm{.}}$$ | + | :$$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$ |
| − | Mit der Substitution $t = \tau + t | + | *Mit der Substitution $t = \tau + t\hspace{0.05cm}'$ ergibt sich: |
| − | $$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d }}}\tau \right]} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}ft}\hspace{0.1cm} {\rm{d}}t{\rm{.}}$$ | + | :$$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$ |
| − | + | :Es ist berücksichtigt, dass die Exponentialfunktion unabhängig von der inneren Integrationsvariablen $τ$ ist und diese nur als Faktor des inneren Integrals fungiert. | |
| − | Bezeichnen wir nun das Produkt der beiden Spektren mit $P(f)$ und die dazugehörige Zeitfunktion mit $p(t)$, so lautet das entsprechende Fourierintegral: | + | |
| + | *Bezeichnen wir nun das Produkt der beiden Spektren mit $P(f)$ und die dazugehörige Zeitfunktion mit $p(t)$, so lautet das entsprechende Fourierintegral: | ||
| − | $$P(f) = \int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}ft} \hspace{0.1cm}{\rm{d}}t{\rm{.}}$$ | + | :$$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$ |
| − | Ein Koeffizientenvergleich der beiden Integrale zeigt, dass folgender Zusammenhang | + | *Ein Koeffizientenvergleich der beiden Integrale zeigt, dass folgender Zusammenhang gelten muss: |
| − | $$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d }}\tau{\rm{.}}$$ | + | :$$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$ |
| + | |||
| + | <div align="right">q.e.d.</div>}} | ||
| + | |||
| + | |||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:3.7 Synchrondemodulator|A3.7 Synchrondemodulator]] | ||
| − | + | [[Aufgaben: 3.7Z Rechtecksignal mit Echo|Z3.7 Rechtecksignal mit Echo]] | |
| + | [[Aufgaben:3.8 Dreimal Faltung?|A3.8 Dreimal Faltung?]] | ||
| − | + | [[Aufgaben: 3.8Z Faltung zweier Rechtecke|Z3.8 Faltung zweier Rechtecke]] | |
| + | [[Aufgaben:3.9 Faltung von Rechteck und Gauß|A3.9 Faltung von Rechteck und Gauß]] | ||
| + | [[Aufgaben:3.9Z Gauß gefaltet mit Gauß|Z3.9 Gauß gefaltet mit Gauß]] | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 28. April 2021, 10:37 Uhr
Inhaltsverzeichnis
Faltung im Zeitbereich
Der „Faltungssatz” ist mit das wichtigste Gesetz der Fouriertransformation, dem in vorliegendem Tutorial ein eigenes Unterkapitel gewidmet wird.
Wir betrachten zunächst den Faltungssatz im Zeitbereich und setzen voraus, dass die Spektren zweier Zeitfunktionen $x_1(t)$ und $x_2(t)$ bekannt sind:
- $$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$
Dann gilt für die Zeitfunktion des Produktes $X_1(f) \cdot X_2(f)$:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Hierbei ist $\tau$ eine formale Integrationsvariable mit der Dimension einer Zeit.
$\text{Definition:}$ Die obige Verknüpfung der Zeitfunktion $x_1(t)$ und $x_2(t)$ bezeichnet man als $\text{Faltung}$ und stellt diesen Funktionalzusammenhang mit einem Stern dar:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$
- Damit lässt sich obige Fourierkorrespondenz auch wie folgt schreiben:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
- Die Faltung ist $\text{"kommutativ"}$ ⇒ Die Reihenfolge der Operanden ist vertauschbar:
- $$x_1(t) * x_2(t) =x_2(t) * x_1(t).$$
- Der Beweis folgt am Kapitelende.
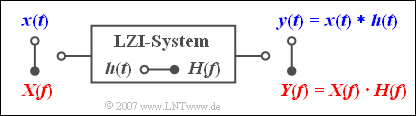
$\text{Beispiel 1:}$ Ein jedes lineare zeitinvariante (LZI-) System kann sowohl durch den Frequenzgang $H(f)$ als auch durch die Impulsantwort $h(t)$ beschrieben werden, wobei der Zusammenhang zwischen diesen beiden Systemgrößen ebenfalls durch die Fouriertransformation gegeben ist.
Legt man an den Eingang ein Signal $x(t)$ mit dem Spektrum $X(f)$ an, so gilt für das Spektrum des Ausgangssignals:
- $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$
Mit dem Faltungssatz ist es möglich, das Ausgangssignal auch direkt im Zeitbereich zu berechnen:
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$
Aus dieser Gleichung geht nochmals hervor, dass die Faltungsoperation „kommutativ” ist.
Faltung im Frequenzbereich
Die Dualität zwischen Zeit– und Frequenzbereich erlaubt auch Aussagen hinsichtlich des Spektrums des Produktsignals:
- $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$
Dieses Resultat lässt sich ähnlich wie der Faltungssatz im Zeitbereich beweisen. Die Integrationsvariable $\nu$ hat aber nun die Dimension einer Frequenz.
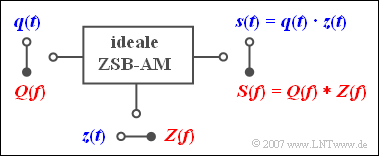
$\text{Beispiel 2:}$ Die Zweiseitenband-Amplitudenmodulation (ZSB-AM) ohne Träger wird durch das skizzierte Modell beschrieben.
- Bei der Zeitbereichsdarstellung (blau) ergibt sich das modulierte Signal $s(t)$ als das Produkt aus dem Nachrichtensignal $q(t)$ und dem (normierten) Trägersignal $z(t)$.
- Nach dem Faltungssatz folgt daraus für den Frequenzbereich (rot), dass das Ausgangsspektrum $S(f)$ gleich dem Faltungsprodukt aus $Q(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ q(t)$ und $Z(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \ z(t)$ ist.
Faltung einer Funktion mit einer Diracfunktion
Sehr einfach wird die Faltungsoperation, wenn einer der beiden Operanden eine Diracfunktion ist. Dies gilt für die Faltung im Zeit– und im Frequenzbereich gleichermaßen.
- Wir betrachten beispielhaft die Faltung einer Funktion $x_1(t)$ mit der Funktion
- $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
- Für die Spektralfunktion des Signals $y(t) = x_1(t) \ast x_2(t)$ gilt dann:
- $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
- Die komplexe Exponentialfunktion führt zur Verschiebung um $T$ ⇒ Verschiebungssatz, der Faktor $\alpha$ zu einer Dämpfung $(\alpha < 1)$ bzw. Verstärkung $(\alpha > 1)$.
- Daraus folgt:
- $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$
$\text{In Worten: }$ Die Faltung einer beliebigen Funktion mit einer Diracfunktion bei $t = T$ ergibt die um $T$ nach rechts verschobene Funktion, wobei noch die Gewichtung der Diracfunktion durch den Faktor $\alpha$ zu berücksichtigen ist.
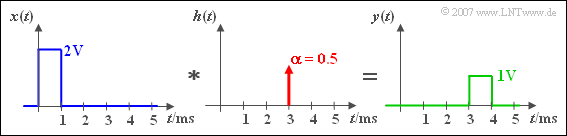
$\text{Beispiel 3:}$ Ein Rechtecksignal $x(t)$ wird durch ein LZI-System um die Laufzeit $\tau = 3\,\text{ ms}$ verzögert und um den Faktor $\alpha = 0.5$ gedämpft.
Verschiebung und Dämpfung erkennt man sowohl
- am Ausgangssignal $y(t)$
- als auch an der Impulsantwort $h(t)$.
Grafische Faltung
Für die Beschreibungen auf dieser Seite wird von folgender Faltungsoperation ausgegangen:
- $$y(t) = x_1 (t) * x_2 (t) $$
- $$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Die Lösung des Faltungsintegrals soll auf grafischem Wege erfolgen Es wird hier vorausgesetzt, dass $x_1(t)$ und $x_2(t)$ zeitkontinuierliche Signale sind.
Dann sind die folgenden Schritte erforderlich:
- Die Zeitvariablen der beiden Funktionen ändern:
$x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. - Zweite Funktion spiegeln: $x_2(\tau) \to x_2(-\tau)$.
- Gespiegelte Funktion um $t$ verschieben: $x_2(-\tau) \to x_2(t-\tau)$.
- Multiplikation der beiden Funktionen $x_1(\tau)$ und $x_2(t-\tau)$.
- Integration über das Produkt bezüglich $\tau$ in den Grenzen von $-\infty$ bis $+\infty$.
Da die Faltung kommutativ ist, kann statt $x_2(\tau)$ auch $x_1(\tau)$ gespiegelt werden.
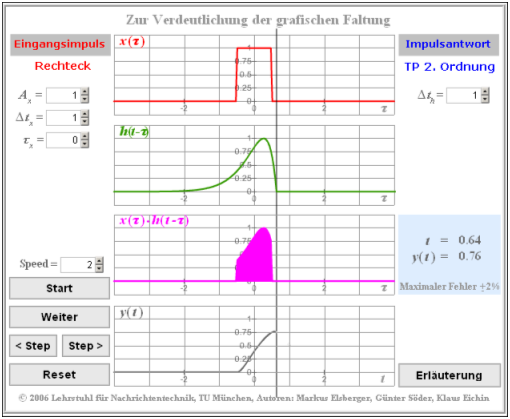
Die Thematik wird auch durch das (neuere) HTML 5–Applet Zur Verdeutlichung der grafischen Faltung veranschaulicht.
$\text{Beispiel 4:}$ Die Vorgehensweise bei der grafischen Faltung wird nun anhand eines ausführlichen Beispiels erklärt:
- Am Eingang eines Filters liege eine Sprungfunktion $x(t) = \gamma(t)$ an.
- Die Impulsantwort des RC-Tiefpasses sei $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$
- Die Zeitachse ist bereits in $\tau$ umbenannt.
Die Grafik zeigt
- rot das Eingangssignal $x(\tau)$,
- blau die Impulsantwort $h(\tau)$,
- grau das Ausgangssignal $y(\tau)$.
Das Ausgangssignal kann zum Beispiel nach folgender Gleichung berechnet werden:
- $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
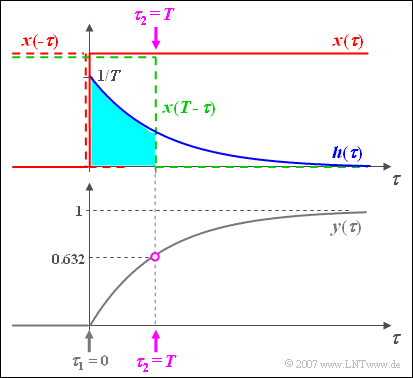
Noch einige Anmerkungen zur grafischen Faltung:
- Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal $x(\tau)$ spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert.
- Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich Null ist, folgt daraus $y(t=0)=0$.
- Für jeden anderen Zeitpunkt $t$ muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$.
Da im Beispiel auch $x(t-\tau)$ nur $0$ und $1$ sein kann, wird die Integration $($allgemein von $\tau_1$ bis $\tau_2)$ sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$ :
- $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$
Die Skizze gilt für $t=T$ und führt zum Ausgangswert $y(t=T) = 1 - 1/\text{e} \approx 0.632$.
Anschauliche Deutung der Faltung
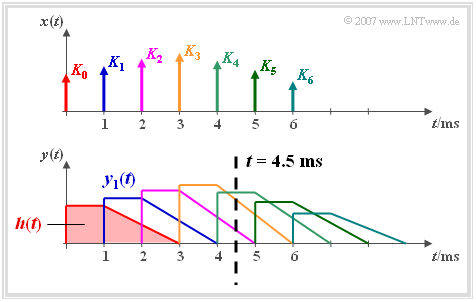
Wir gehen von einer Impulsantwort $h(t)$ aus, die zunächst eine Millisekunde lang konstant ist und dann bis zur Zeit $t = 3 \,\text{ms}$ linear auf Null abfällt.
- Legt man an den Eingang dieses Tiefpassfilters einen Diracimpuls $K_0 \cdot \delta(t)$ an, so ist das Ausgangssignal $y(t)$ formgleich mit der Impulsantwort $h(t)$. Der Sachverhalt ist im Bild rot dargestellt.
- Ein um $T= 1 \,\text{ms}$ späterer Diracimpuls mit Gewicht $K_1 > K_0$ hat das blau gezeichnete Ausgangssignal $y_1(t)$ zur Folge, das gegenüber dem roten Signal verzögert und in der Amplitude vergrößert ist.
Wir betrachten nun das aus sieben verschieden gewichteten und verschobenen Diracimpulsen bestehende Eingangssignal
- $$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$
das als zeitdiskrete Näherung eines zeitkontinuierlichen Signals aufgefasst werden kann.
Das Signal am Ausgang des linearen Systems ist die Summe der sieben im Bild verschiedenfarbig markierten Teilsignale:
- $$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$
Wir betrachten nun den Signalwert zur Zeit $t = 4.5T$ (siehe Strichpunktierung):
- $$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$
Dieser Signalwert wird somit nur durch die Eingangssignalwerte $K_2$, $K_3$ und $K_4$ bestimmt. Der Einfluss
- von $K_4$ ist wegen $h(0.5T) = 1$ am stärksten,
- von $K_3$ ist wegen $h(1.5T) = 0.75$ weniger stark,
- von $K_2$ ist wegen $h(2.5T) = 0.25$ am geringsten.
Beweis des Faltungssatzes
$\text{Definition: }$ Man nennt die folgende Verknüpfung der Zeitfunktionen $x_1(t)$ und $x_2(t)$ die $\text{Faltung}$ und stellt diesen Funktionalzusammenhang mit einem Stern dar:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
Daraus ergibt sich die folgende Fourierkorrespondenz:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
$\text{Beweis: }$ Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen:
- $$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$
- $$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t{0.05cm}'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$
- Bildet man das Produkt der Spektralfunktionen, so erhält man:
- $$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$
- Mit der Substitution $t = \tau + t\hspace{0.05cm}'$ ergibt sich:
- $$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$
- Es ist berücksichtigt, dass die Exponentialfunktion unabhängig von der inneren Integrationsvariablen $τ$ ist und diese nur als Faktor des inneren Integrals fungiert.
- Bezeichnen wir nun das Produkt der beiden Spektren mit $P(f)$ und die dazugehörige Zeitfunktion mit $p(t)$, so lautet das entsprechende Fourierintegral:
- $$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$
- Ein Koeffizientenvergleich der beiden Integrale zeigt, dass folgender Zusammenhang gelten muss:
- $$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$
Aufgaben zum Kapitel
A3.9 Faltung von Rechteck und Gauß