Signaldarstellung/Grundsätzliches zu Tiefpass- und Bandpass-Signalen: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL # == | == # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL # == | ||
<br> | <br> | ||
| − | Im dritten Hauptkapitel: [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation|Aperiodische Signale – Impulse]] wurden meist stillschweigend tiefpassartige Signale vorausgesetzt, das heißt solche Signale, deren Spektralfunktionen im Bereich um die Frequenz $f = 0$ liegen. Insbesondere bei optischer Übertragung und bei Funkübertragungssystemen – aber nicht nur bei diesen – liegen die Sendesignale jedoch im Bereich um eine Trägerfrequenz $f_{\rm T}$. Solche Signale bezeichnet man als $\text{Bandpass-Signale}$. | + | Im dritten Hauptkapitel: [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation|"Aperiodische Signale – Impulse"]] wurden meist stillschweigend tiefpassartige Signale vorausgesetzt, das heißt solche Signale, deren Spektralfunktionen im Bereich um die Frequenz $f = 0$ liegen. Insbesondere bei optischer Übertragung und bei Funkübertragungssystemen – aber nicht nur bei diesen – liegen die Sendesignale jedoch im Bereich um eine Trägerfrequenz $f_{\rm T}$. Solche Signale bezeichnet man als $\text{Bandpass-Signale}$. |
Alle im letzten Kapitel dargelegten Gesetze der Fouriertransformation und –rücktransformation gelten für bandpassartige Signale in gleicher Weise. Daneben gibt es aber auch einige Besonderheiten der Bandpass-Signale, deren Beachtung zu einer einfacheren Beschreibung führen können. | Alle im letzten Kapitel dargelegten Gesetze der Fouriertransformation und –rücktransformation gelten für bandpassartige Signale in gleicher Weise. Daneben gibt es aber auch einige Besonderheiten der Bandpass-Signale, deren Beachtung zu einer einfacheren Beschreibung führen können. | ||
| Zeile 91: | Zeile 91: | ||
| − | ==Beschreibung eines | + | ==Beschreibung eines Bandpass-Signals mittels Tiefpass-Signalen== |
<br> | <br> | ||
Wir betrachten zwei Tiefpass–Spektren $X_1(f)$ und $X_2(f)$ mit den Bandbreiten $B_1$ und $B_2$ entsprechend der linken Grafik. | Wir betrachten zwei Tiefpass–Spektren $X_1(f)$ und $X_2(f)$ mit den Bandbreiten $B_1$ und $B_2$ entsprechend der linken Grafik. | ||
| − | [[Datei:P_ID684__Sig_T_4_1_S3a.png| | + | [[Datei:P_ID684__Sig_T_4_1_S3a.png|right|Erzeugung eines Bandpass-Spektrums aus Tiefpass-Spektren]] |
Aus dieser Darstellung ist zu erkennen: | Aus dieser Darstellung ist zu erkennen: | ||
| − | *Sind $X_1(f)$ und $X_2(f)$ bis zu einer Frequenz $f_{12}$ identisch, so beschreibt die Differenz ein Bandpass | + | *Sind $X_1(f)$ und $X_2(f)$ bis zu einer Frequenz $f_{12}$ identisch, so beschreibt die Differenz ein Bandpass–Spektrum mit Bandbreite $B_{\rm BP} = B_1 - f_{12}$. Entsprechend der rechten Grafik gilt dann: |
:$$X_{\rm BP}(f) = X_1(f) -X_2(f).$$ | :$$X_{\rm BP}(f) = X_1(f) -X_2(f).$$ | ||
| − | *Aufgrund der Linearität der Fouriertransformation gilt für die zum Bandpass | + | *Aufgrund der Linearität der Fouriertransformation gilt für die zum Bandpass–Spektrum $X_{\rm BP}(f)$ zugehörige Zeitfunktion: |
:$$x_{\rm BP}(t) = x_1(t) - x_2(t).$$ | :$$x_{\rm BP}(t) = x_1(t) - x_2(t).$$ | ||
| − | *Aus der Fouriertransformation folgt allgemein, dass das Integral über die Zeitfunktion gleich dem Spektralwert bei $f = 0$ ist. Bei jedem Bandpass–Signal ist demzufolge dieses Integral stets Null: | + | *Aus der Fouriertransformation folgt allgemein, dass das Integral über die Zeitfunktion gleich dem Spektralwert bei $f = 0$ ist. Bei jedem Bandpass–Signal ist demzufolge dieses Integral stets Null: |
:$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | :$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | ||
d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$ | d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$ | ||
| Zeile 108: | Zeile 108: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 3:}$ | $\text{Beispiel 3:}$ | ||
| − | Die roten Kurven in den beiden Grafiken zeigen das Bandpass | + | Die roten Kurven in den beiden Grafiken zeigen das Bandpass–Spektrum $X_{\rm BP}(f)$ und die zugehörige Zeitfunktion |
:$$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm | :$$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm | ||
| Zeile 116: | Zeile 116: | ||
\hspace{0.05cm}{\rm kHz} \cdot t).$$ | \hspace{0.05cm}{\rm kHz} \cdot t).$$ | ||
| − | + | Ebenfalls dargestellt sind die zwei Tiefpass–Spektren und –Signale. | |
| − | + | [[Datei:P_ID685__Sig_T_4_1_S3b_neu.png|right|frame|Tiefpass– und Bandpass–Spektrum und zugehörige Signale]] | |
| − | *Die blau-gepunktete Kurve in der linken Grafik stellt das trapezförmige Spektrum $X_1(f)$ dar | + | |
| − | *Die blau-gepunktete Kurve in der rechten Grafik zeigt das dazugehörige Tiefpass–Signal $x_1(t)$. Der Signalwert bei $t = 0$ entspricht der blauen Trapezfläche des Spektrums $X_1(f)$: | + | Man erkennt aus diesen Bildern: |
| + | *Die blau-gepunktete Kurve in der linken Grafik stellt das trapezförmige Spektrum $X_1(f)$ dar. Die äquivalente Bandbreite beträgt $\Delta f_1= 10 \,\text{kHz}$ und der Rolloff-Faktor ist $r_1 = 0.2$. | ||
| + | *Die blau-gepunktete Kurve in der rechten Grafik zeigt das dazugehörige Tiefpass–Signal $x_1(t)$. Der Signalwert bei $t = 0$ entspricht der blauen Trapezfläche des Spektrums $X_1(f)$: | ||
:$$x_1(t = 0) = 10 \,\text{V}.$$ | :$$x_1(t = 0) = 10 \,\text{V}.$$ | ||
| − | *Die grüne Kurve gilt für das Rechteckspektrum $X_2(f)$ mit der äquivalenten Bandbreite $\Delta f_2= 2 \,\text{kHz}$. Das dazugehörige Zeitsignal $x_2(t)$ verläuft $\sin(x)/x$–förmig und es gilt: | + | *Die grüne Kurve gilt für das Rechteckspektrum $X_2(f)$ mit der äquivalenten Bandbreite $\Delta f_2= 2 \,\text{kHz}$. Das dazugehörige Zeitsignal $x_2(t)$ verläuft $\sin(x)/x$–förmig und es gilt: |
:$$x_2(t = 0) = 2 \,\text{V}.$$ | :$$x_2(t = 0) = 2 \,\text{V}.$$ | ||
| − | Die rote Kurve für das bandpassartige Signal ergibt sich links wie rechts als Differenz zwischen blauer und grüner Kurve. Entsprechend ist | + | *Die rote Kurve für das bandpassartige Signal ergibt sich links wie rechts als Differenz zwischen blauer und grüner Kurve. Entsprechend ist |
:$$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$ | :$$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$ | ||
:$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | :$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | ||
| Zeile 130: | Zeile 132: | ||
| − | ==Synthese von | + | ==Synthese von Bandpass-Signalen aus dem äquivalenten Tiefpass-Signal== |
<br> | <br> | ||
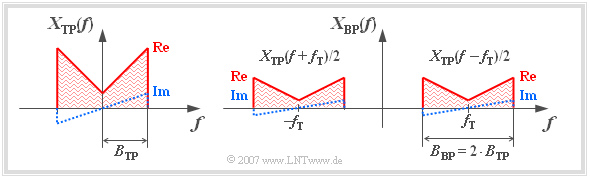
| − | Wir betrachten ein Tiefpass-Signal $x_{\rm TP}(t)$ mit Spektrum $X_{\rm TP}(f)$ entsprechend der linken Skizze. | + | Wir betrachten ein Tiefpass-Signal $x_{\rm TP}(t)$ mit Spektrum $X_{\rm TP}(f)$ entsprechend der linken Skizze. |
| + | |||
| + | [[Datei:P_ID2724__Sig_T_4_1_S4a.png|center|frame|Ein Bandpass–Spektrum ergibt sich durch beidseitiges Verschieben eines TP–Spektrums]] | ||
Multipliziert man dieses Signal mit einer (dimensionslosen) harmonischen Schwingung | Multipliziert man dieses Signal mit einer (dimensionslosen) harmonischen Schwingung | ||
| Zeile 147: | Zeile 151: | ||
Hierbei ist berücksichtigt, dass die [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltung]] der Spektralfunktion $X_{\rm TP}(f)$ mit der verschobenen Diracfunktion $\delta (f - f_\rm {T})$ die um $f_\rm {T}$ nach rechts verschobene Funktion $X_{\rm TP}(f-f_\rm {T})$ ergibt. | Hierbei ist berücksichtigt, dass die [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltung]] der Spektralfunktion $X_{\rm TP}(f)$ mit der verschobenen Diracfunktion $\delta (f - f_\rm {T})$ die um $f_\rm {T}$ nach rechts verschobene Funktion $X_{\rm TP}(f-f_\rm {T})$ ergibt. | ||
| − | + | Aus der rechten Spektralbereichsdarstellung erkennt man eindeutig, dass $x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T}\cdot t)$ ein Bandpass-Signal ist. Die Einhüllende von $x_{\rm BP}(t)$ ist durch den Betrag $|x_{\rm TP}(t)|$ gegeben. Anwendung findet dieses Prinzip bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Amplitudenmodulation ohne Träger]], die im Buch „Modulationsverfahren” behandelt wird. | |
| − | |||
| − | Aus der rechten Spektralbereichsdarstellung erkennt man eindeutig, dass | ||
| − | |||
| − | |||
| − | \cdot t)$ | ||
| − | |||
| − | ein Bandpass-Signal ist. Die Einhüllende von $x_{\rm BP}(t)$ ist durch den Betrag $|x_{\rm TP}(t)|$ gegeben. | ||
| − | Anwendung findet dieses Prinzip | ||
Aus obiger Grafik erkennt man: | Aus obiger Grafik erkennt man: | ||
*Das Spektrum $X_{\rm BP}(f)$ hat im Bereich um die Trägerfrequenz $f_{\rm T}$ die gleiche Form wie $X_{\rm TP}(f)$ im Bereich um $f = 0$, ist aber gegenüber dem Tiefpass-Spektrum um den Faktor $2$ gedämpft. | *Das Spektrum $X_{\rm BP}(f)$ hat im Bereich um die Trägerfrequenz $f_{\rm T}$ die gleiche Form wie $X_{\rm TP}(f)$ im Bereich um $f = 0$, ist aber gegenüber dem Tiefpass-Spektrum um den Faktor $2$ gedämpft. | ||
| − | *Da $X_{\rm TP}(f)$ bezogen auf $f = 0$ einen geraden Real– und einen ungeraden Imaginärteil besitzt, weist das | + | *Da $X_{\rm TP}(f)$ bezogen auf $f = 0$ einen geraden Real– und einen ungeraden Imaginärteil besitzt, weist das BP-Spektrum $X_{\rm BP}(f)$ gleiche Symmetrieeigenschaften auf – allerdings nun bezogen auf die Trägerfrequenz $f_{\rm T}$. |
| − | *Auch $X_{\rm BP}(f)$ besitzt Anteile bei negativen Frequenzen. Da das zugehörige Signal $x_{\rm BP}(t)$ gemäß obiger Gleichung ebenfalls reell ist, muss auch $X_{\rm BP}(f)$ bezüglich der Frequenz $f = 0$ einen geraden Real– und einen ungeraden Imaginärteil besitzen. | + | *Auch $X_{\rm BP}(f)$ besitzt Anteile bei negativen Frequenzen. Da das zugehörige Signal $x_{\rm BP}(t)$ gemäß obiger Gleichung ebenfalls reell ist, muss auch $X_{\rm BP}(f)$ bezüglich der Frequenz $f = 0$ einen geraden Real– und einen ungeraden Imaginärteil besitzen. |
*Die Bandbreite des Bandpass-Signals ist doppelt so groß wie die des Tiefpass-Signals: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Voraussetzung für die Gültigkeit dieser Aussage ist, dass die Trägerfrequenz $f_{\rm T}$ mindestens um den Faktor $2$ größer ist als die maximale Frequenz $(B_{\rm TP})$ des Signals $x_{\rm TP}(t)$. | *Die Bandbreite des Bandpass-Signals ist doppelt so groß wie die des Tiefpass-Signals: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Voraussetzung für die Gültigkeit dieser Aussage ist, dass die Trägerfrequenz $f_{\rm T}$ mindestens um den Faktor $2$ größer ist als die maximale Frequenz $(B_{\rm TP})$ des Signals $x_{\rm TP}(t)$. | ||
| Zeile 167: | Zeile 163: | ||
$\text{Beispiel 4:}$ Ein Tiefpass-Signal besitze diskrete Spektralanteile bei $f_1 = 1\,\text{ kHz}, \, f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ und $f_4 = 4\,\text{ kHz}$: | $\text{Beispiel 4:}$ Ein Tiefpass-Signal besitze diskrete Spektralanteile bei $f_1 = 1\,\text{ kHz}, \, f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ und $f_4 = 4\,\text{ kHz}$: | ||
| − | :$$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + | + | [[Datei:P_ID687__Sig_T_4_1_S4b.png|right|frame|ZSB-AM-Signal mit unterschiedlichen Trägerfrequenzen]] |
| + | |||
| + | :$$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + $$ | ||
| + | :$$\hspace{1.5cm}+ \ 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + | ||
120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ | 120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ | ||
\circ}).$$ | \circ}).$$ | ||
| Zeile 173: | Zeile 172: | ||
Das dazugehörige Spektrum $X_{\rm TP}(f)$ ist wegen der von Null verschiedenen Phasenlagen komplex. | Das dazugehörige Spektrum $X_{\rm TP}(f)$ ist wegen der von Null verschiedenen Phasenlagen komplex. | ||
| − | + | *Multipliziert man das (blaue) Signal $x_{\rm TP}(t)$ mit einem Cosinussignal der Amplitude $1$ und der Frequenz $f_{\rm T} = 20 \,\text{kHz}$, so ergibt sich das (rote) Bandpass-Signal gemäß der oberen Grafik. | |
| − | |||
| − | *Multipliziert man $x_{\rm TP}(t)$ mit einem Cosinussignal der Amplitude $1$ und der Frequenz $f_{\rm T} = 20 \,\text{kHz}$, so ergibt sich das Bandpass-Signal gemäß der oberen Grafik. | ||
*Die untere Skizze gilt für das Bandpass-Signal mit der Trägerfrequenz $f_{\rm T} = 100 \,\text{kHz}$. | *Die untere Skizze gilt für das Bandpass-Signal mit der Trägerfrequenz $f_{\rm T} = 100 \,\text{kHz}$. | ||
*In beiden Darstellungen sind die Funktionsverläufe $\pm \vert x_{\rm TP}(t) \vert $ als Einhüllende der Bandpass-Signale zu erkennen. }} | *In beiden Darstellungen sind die Funktionsverläufe $\pm \vert x_{\rm TP}(t) \vert $ als Einhüllende der Bandpass-Signale zu erkennen. }} | ||
| − | ''Hinweis'': Die Thematik dieses Kapitels wird im Lernvideo [[Eigenschaften_von_Tiefpass-_und_Bandpasssignalen_(Lernvideo)|Eigenschaften von Tiefpass– und Bandpass–Signalen]] behandelt. | + | ''Hinweis'': Die Thematik dieses Kapitels wird im Lernvideo [[Eigenschaften_von_Tiefpass-_und_Bandpasssignalen_(Lernvideo)|Eigenschaften von Tiefpass– und Bandpass–Signalen]] behandelt. |
| − | Weitere Informationen zum Thema, zahlreiche Aufgaben und Simulationen finden Sie im Versuch „Analoge Modulationsverfahren” des Praktikums „Simulation digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | + | Weitere Informationen zum Thema, zahlreiche Aufgaben und Simulationen finden Sie im Versuch „Analoge Modulationsverfahren” des Praktikums „Simulation digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf |
*dem Windows-Programm [http://www.lntwww.de/downloads/Sonstiges/Programme/AMV.zip AMV] ⇒ Link verweist auf die ZIP-Version des Programms und | *dem Windows-Programm [http://www.lntwww.de/downloads/Sonstiges/Programme/AMV.zip AMV] ⇒ Link verweist auf die ZIP-Version des Programms und | ||
*der zugehörigen [http://www.lntwww.de/downloads/Sonstiges/Texte/Analoge_Modulationsverfahren.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version; insgesamt 86 Seiten. | *der zugehörigen [http://www.lntwww.de/downloads/Sonstiges/Texte/Analoge_Modulationsverfahren.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version; insgesamt 86 Seiten. | ||
Aktuelle Version vom 4. Mai 2021, 17:58 Uhr
Inhaltsverzeichnis
# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
Im dritten Hauptkapitel: "Aperiodische Signale – Impulse" wurden meist stillschweigend tiefpassartige Signale vorausgesetzt, das heißt solche Signale, deren Spektralfunktionen im Bereich um die Frequenz $f = 0$ liegen. Insbesondere bei optischer Übertragung und bei Funkübertragungssystemen – aber nicht nur bei diesen – liegen die Sendesignale jedoch im Bereich um eine Trägerfrequenz $f_{\rm T}$. Solche Signale bezeichnet man als $\text{Bandpass-Signale}$.
Alle im letzten Kapitel dargelegten Gesetze der Fouriertransformation und –rücktransformation gelten für bandpassartige Signale in gleicher Weise. Daneben gibt es aber auch einige Besonderheiten der Bandpass-Signale, deren Beachtung zu einer einfacheren Beschreibung führen können.
Dieses Kapitel beinhaltet im Einzelnen:
- die Aufzählung von Unterschieden und Gemeinsamkeiten von Tiefpass– und Bandpass–Signalen,
- die Synthese von Bandpass–Signalen aus dem äquivalenten Tiefpass–Signal,
- das analytische Signal und die zugehörige Spektralfunktion,
- das äquivalente Tiefpass–Signal im Zeit– und Frequenzbereich, und schließlich
- die Darstellung von analytischem Signal/äquivalentem Tiefpass–Signal in der komplexen Ebene.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Analoge Modulationsverfahren” des Praktikums „Simulation Digitaller Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Windows-Programm AMV ⇒ Link verweist auf die ZIP-Version des Programms und
- der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version (Insgesamt 86 Seiten).
Bedeutung der Bandpass-Signale für die Nachrichentechnik
In den bisherigen Kapiteln dieses Buches wurden bisher fast nur Signale betrachtet, deren Spektren in einem engen Bereich um die Frequenz $f = 0$ liegen. Beispiele hierfür sind analoge Sprach–, Musik– und Bildsignale, die man alle – trotz ihrer unterschiedlichen Bandbreiten – als $\text{Tiefpass-Signale}$ bezeichnen kann.
Will man ein solches Tiefpass-Signal zu einer räumlich entfernten Sinke übertragen, so muss das Signal unter Umständen in eine andere Frequenzlage umgesetzt werden. Dafür kann es mehrere Gründe geben:
- Häufig ist der Übertragungskanal für die direkte Übertragung des Quellensignals im originalen Frequenzband ungeeignet, da dieses für ihn ungünstige Frequenzen beinhaltet. Erst durch eine Frequenzverschiebung mittels eines so genannten "Modulators" wird eine Übertragung ermöglicht.
- Man kann einen einzigen Übertragungskanal auch zur gleichzeitigen Übertragung mehrerer Signale nutzen, wenn diese sendeseitig mit verschiedenen Trägerfrequenzen moduliert werden. Man nennt dieses Verfahren Frequenzmultiplex (englisch: "Frequency Division Multiple Access", $\text{FDMA)}$.
- Die Übertragungsqualität kann gegenüber dem einfachsten analogen Verfahren Amplitudenmodulation $\text{(AM)}$ auf Kosten einer größeren Bandbreite verbessert und somit ein größeres "Signal-zu-Rauschverhältnis" erzielt werden. Beispiele sind die analoge Frequenzmodulation $\text{(FM)}$ und die digitale Pulscodemodulation $\text{(PCM)}$.
$\text{Festzuhalten ist:}$ Die Sendesignale vieler Übertragungsverfahren sind $\text{Bandpass-Signale}$.
Hinweis: Dem Autor ist durchaus bewusst, dass es nach der letzten Rechtschreibreform „Tiefpasssignal” und „Bandpasssignal” heißen müsste. Um diese unschönen Konstrukte zu vermeiden, verwenden wir im Folgenden meist die Schreibweisen „Tiefpass–Signal” und „Bandpass–Signal”, manchmal auch „TP–Signal” und „BP–Signal”.
$\text{Beispiel 1: Zur Klassifizierung von Signalen hinsichtlich „Tiefpass” und „Bandpass”}$
(a) "Sprache" und "Musik" sind Tiefpass–Signale mit einer Bandbreite von $\text{20 kHz}$ (bei sehr guter Qualität). Da eine Funkübertragung aber erst ab ca. $\text{100 kHz}$ möglich ist, erfolgt bei Analogsystemen vor der Übertragung eine Umsetzung auf Trägerfrequenzen zwischen
- $\text{0.525 ... 1.61 MHz}$ $($Mittelwellenrundfunk, Amplitudenmodulation, Kanalabstand $\text{9 kHz})$,
- $\text{87.5 ... 108 MHz}$ $($Rundfunk auf UKW, Frequenzmodulation, Kanalabstand $\text{300 kHz})$.
(b) "TV-Bildsignale" weisen eine größere Bandbreite auf, zum Beispiel $\text{5 MHz}$. Auch hier erfolgt vor der Ton– und Bildübertragung eine Frequenzbandverschiebung durch Trägerfrequenzen zwischen
- $\text{41 ... 68 / 174 ... 230 MHz}$ (Fernsehen, VHF-Band, Kanalabstand $\text{7 MHz})$,
- $\text{470 ... 850 MHz}$ $($Fernsehen, UHF-Band, Kanalabstand $\text{8 MHz})$.
(c) Beim "GSM-Mobilfunk" liegen die Trägerfrequenzen im D-Band bei $\text{900 MHz}$ und im E-Band bei $\text{1800 MHz}$.
(d) Bei "optischer Übertragung" werden die elektrischen Signale in Licht gewandelt, also auf Frequenzen zwischen ca. $\text{200 THz}$ und $\text{350 THz}$ $($entsprechend $\text{1.55 µm ... 0.85 µm}$ Wellenlänge).
Eigenschaften von Bandpass-Signalen
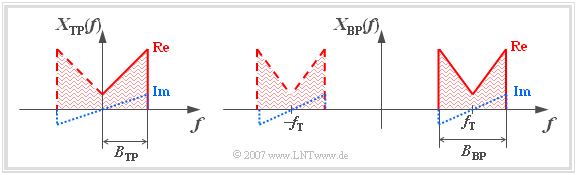
Auf dieser Seite werden – ohne Anspruch auf Vollständigkeit – einige Eigenschaften von Bandpass–Signalen zusammengestellt und den Tiefpass–Signalen vergleichend gegenübergestellt. Dabei gehen wir von den Spektralfunktionen $X_{\rm TP}(f)$ und $X_{\rm BP}(f)$ gemäß der folgenden Skizze aus.
Zu der Grafik ist anzumerken:
- Die Dreiecksform der dargestellten Spektren ist schematisch zu verstehen und soll nur das belegte Frequenzband kennzeichnen. Daraus sollte also nicht geschlossen werden, dass alle Frequenzen innerhalb des Bandes tatsächlich belegt sind und dass alle Spektralfunktionen linear mit der Frequenz $f$ zunehmen.
- Die zugehörigen Zeitfunktionen $x_{\rm TP}(t)$ und $x_{\rm BP}(t)$ seien vorerst reell. Das bedeutet, dass nach dem Zuordnungssatz die Spektralfunktionen $X_{\rm TP}(f)$ und $X_{\rm BP}(f)$ – bezogen auf die Frequenz $f = 0$ – jeweils einen geraden Realteil und einen ungeraden Imaginärteil besitzen.
- Als Bandbreite $B_{\rm TP}$ bzw. $B_{\rm BP}$ bezeichnen wir für Tiefpass und Bandpass gleichermaßen das belegte Frequenzband bei den positiven Frequenzen (in der Grafik: durchgezogene Kurvenverläufe).
$\text{Beispiel 2:}$ Es folgt ein Beispiel mit diskreten Spektrallinien.
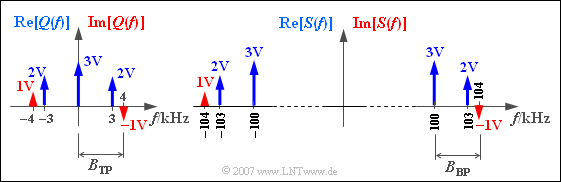
Die linke Grafik zeigt das Spektrum $Q(f)$ des Nachrichtensignals
- $$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \cdot 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi \cdot 4\hspace{0.05cm}{\rm kHz} \cdot t). $$
Die diskreten Spektrallinien des Realteils ⇒ ${\rm Re}\big[Q(f)\big]$ sind blau dargestellt und diejenigen des Imaginärteils ⇒ ${\rm Im}\big[Q(f)\big]$ rot.
Rechts dargestellt ist das Spektrum $S(f)$ nach Einseitenband–Amplitudenmodulation $\text{(ESB–AM)}$ mit der Trägerfrequenz $f_{\rm T} = 100 \,\text{kHz}$. Eine Beschreibung dieses Übertragungssystems finden Sie im Kapitel Hüllkurvendemodulation des Buches „Modulationsverfahren”.
- Nach dieser Beschreibung ist $q(t)$ eindeutig ein Tiefpass–Signal und $s(t)$ ein Bandpass–Signal. Die Bandbreiten sind jeweils $B_{\rm TP} = B_{\rm BP} = 4 \,\text{kHz}$.
- Die Signale $q(t)$ und $s(t)$ sind zudem reell, da sowohl $Q(f)$ als auch $S(f)$ einen geraden Real- und einen ungeraden Imaginärteil aufweisen.
- Würde beim Quellensignal der Gleichanteil $(3 \,\text{V})$ fehlen, so würde man sinnvollerweise $q(t)$ noch immer als tiefpassartig bezeichnen.
- Ohne Kenntnis der Aufgabenstellung könnte man $q(t)$ dann aber auch als Bandpass–Signal mit der Bandbreite $B_{\rm BP} = 1 \,\text{kHz}$ auffassen.
Dieses Beispiel zeigt, dass es kein eindeutiges mathematisches Unterscheidungsmerkmal zwischen Tiefpass– und Bandpass–Signalen gibt.
Beschreibung eines Bandpass-Signals mittels Tiefpass-Signalen
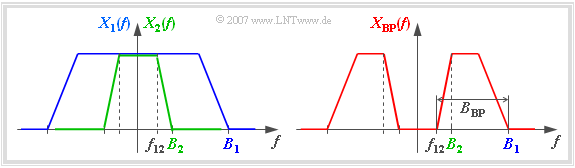
Wir betrachten zwei Tiefpass–Spektren $X_1(f)$ und $X_2(f)$ mit den Bandbreiten $B_1$ und $B_2$ entsprechend der linken Grafik.
Aus dieser Darstellung ist zu erkennen:
- Sind $X_1(f)$ und $X_2(f)$ bis zu einer Frequenz $f_{12}$ identisch, so beschreibt die Differenz ein Bandpass–Spektrum mit Bandbreite $B_{\rm BP} = B_1 - f_{12}$. Entsprechend der rechten Grafik gilt dann:
- $$X_{\rm BP}(f) = X_1(f) -X_2(f).$$
- Aufgrund der Linearität der Fouriertransformation gilt für die zum Bandpass–Spektrum $X_{\rm BP}(f)$ zugehörige Zeitfunktion:
- $$x_{\rm BP}(t) = x_1(t) - x_2(t).$$
- Aus der Fouriertransformation folgt allgemein, dass das Integral über die Zeitfunktion gleich dem Spektralwert bei $f = 0$ ist. Bei jedem Bandpass–Signal ist demzufolge dieses Integral stets Null:
- $$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$
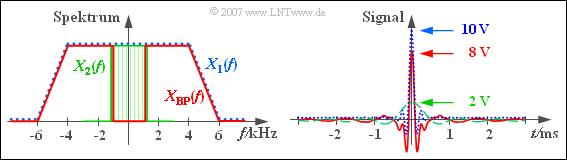
$\text{Beispiel 3:}$ Die roten Kurven in den beiden Grafiken zeigen das Bandpass–Spektrum $X_{\rm BP}(f)$ und die zugehörige Zeitfunktion
- $$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot 10 \hspace{0.05cm}{\rm kHz} \cdot t) \cdot {\rm si} ( \pi \cdot 2 \hspace{0.05cm}{\rm kHz} \cdot t) - 2\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot 2 \hspace{0.05cm}{\rm kHz} \cdot t).$$
Ebenfalls dargestellt sind die zwei Tiefpass–Spektren und –Signale.
Man erkennt aus diesen Bildern:
- Die blau-gepunktete Kurve in der linken Grafik stellt das trapezförmige Spektrum $X_1(f)$ dar. Die äquivalente Bandbreite beträgt $\Delta f_1= 10 \,\text{kHz}$ und der Rolloff-Faktor ist $r_1 = 0.2$.
- Die blau-gepunktete Kurve in der rechten Grafik zeigt das dazugehörige Tiefpass–Signal $x_1(t)$. Der Signalwert bei $t = 0$ entspricht der blauen Trapezfläche des Spektrums $X_1(f)$:
- $$x_1(t = 0) = 10 \,\text{V}.$$
- Die grüne Kurve gilt für das Rechteckspektrum $X_2(f)$ mit der äquivalenten Bandbreite $\Delta f_2= 2 \,\text{kHz}$. Das dazugehörige Zeitsignal $x_2(t)$ verläuft $\sin(x)/x$–förmig und es gilt:
- $$x_2(t = 0) = 2 \,\text{V}.$$
- Die rote Kurve für das bandpassartige Signal ergibt sich links wie rechts als Differenz zwischen blauer und grüner Kurve. Entsprechend ist
- $$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$
- $$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$
Synthese von Bandpass-Signalen aus dem äquivalenten Tiefpass-Signal
Wir betrachten ein Tiefpass-Signal $x_{\rm TP}(t)$ mit Spektrum $X_{\rm TP}(f)$ entsprechend der linken Skizze.
Multipliziert man dieses Signal mit einer (dimensionslosen) harmonischen Schwingung
- $$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} Z(f) = {1}/{2}\cdot \delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$
so ergibt sich nach dem Faltungssatz für das Spektrum des Signals $x_{\rm BP}(t) = x_{\rm TP}(t) \cdot z(t)$:
- $$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$
Hierbei ist berücksichtigt, dass die Faltung der Spektralfunktion $X_{\rm TP}(f)$ mit der verschobenen Diracfunktion $\delta (f - f_\rm {T})$ die um $f_\rm {T}$ nach rechts verschobene Funktion $X_{\rm TP}(f-f_\rm {T})$ ergibt.
Aus der rechten Spektralbereichsdarstellung erkennt man eindeutig, dass $x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T}\cdot t)$ ein Bandpass-Signal ist. Die Einhüllende von $x_{\rm BP}(t)$ ist durch den Betrag $|x_{\rm TP}(t)|$ gegeben. Anwendung findet dieses Prinzip bei der Amplitudenmodulation ohne Träger, die im Buch „Modulationsverfahren” behandelt wird.
Aus obiger Grafik erkennt man:
- Das Spektrum $X_{\rm BP}(f)$ hat im Bereich um die Trägerfrequenz $f_{\rm T}$ die gleiche Form wie $X_{\rm TP}(f)$ im Bereich um $f = 0$, ist aber gegenüber dem Tiefpass-Spektrum um den Faktor $2$ gedämpft.
- Da $X_{\rm TP}(f)$ bezogen auf $f = 0$ einen geraden Real– und einen ungeraden Imaginärteil besitzt, weist das BP-Spektrum $X_{\rm BP}(f)$ gleiche Symmetrieeigenschaften auf – allerdings nun bezogen auf die Trägerfrequenz $f_{\rm T}$.
- Auch $X_{\rm BP}(f)$ besitzt Anteile bei negativen Frequenzen. Da das zugehörige Signal $x_{\rm BP}(t)$ gemäß obiger Gleichung ebenfalls reell ist, muss auch $X_{\rm BP}(f)$ bezüglich der Frequenz $f = 0$ einen geraden Real– und einen ungeraden Imaginärteil besitzen.
- Die Bandbreite des Bandpass-Signals ist doppelt so groß wie die des Tiefpass-Signals: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Voraussetzung für die Gültigkeit dieser Aussage ist, dass die Trägerfrequenz $f_{\rm T}$ mindestens um den Faktor $2$ größer ist als die maximale Frequenz $(B_{\rm TP})$ des Signals $x_{\rm TP}(t)$.
$\text{Beispiel 4:}$ Ein Tiefpass-Signal besitze diskrete Spektralanteile bei $f_1 = 1\,\text{ kHz}, \, f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ und $f_4 = 4\,\text{ kHz}$:
- $$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + $$
- $$\hspace{1.5cm}+ \ 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + 120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ \circ}).$$
Das dazugehörige Spektrum $X_{\rm TP}(f)$ ist wegen der von Null verschiedenen Phasenlagen komplex.
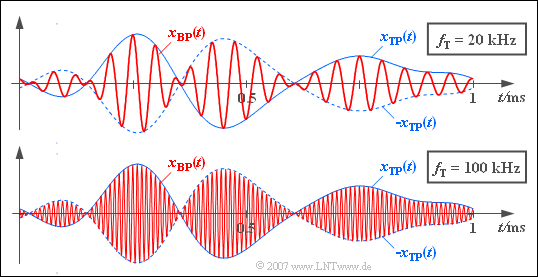
- Multipliziert man das (blaue) Signal $x_{\rm TP}(t)$ mit einem Cosinussignal der Amplitude $1$ und der Frequenz $f_{\rm T} = 20 \,\text{kHz}$, so ergibt sich das (rote) Bandpass-Signal gemäß der oberen Grafik.
- Die untere Skizze gilt für das Bandpass-Signal mit der Trägerfrequenz $f_{\rm T} = 100 \,\text{kHz}$.
- In beiden Darstellungen sind die Funktionsverläufe $\pm \vert x_{\rm TP}(t) \vert $ als Einhüllende der Bandpass-Signale zu erkennen.
Hinweis: Die Thematik dieses Kapitels wird im Lernvideo Eigenschaften von Tiefpass– und Bandpass–Signalen behandelt.
Weitere Informationen zum Thema, zahlreiche Aufgaben und Simulationen finden Sie im Versuch „Analoge Modulationsverfahren” des Praktikums „Simulation digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Windows-Programm AMV ⇒ Link verweist auf die ZIP-Version des Programms und
- der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; insgesamt 86 Seiten.
Aufgaben zum Kapitel
Aufgabe 4.1: Tiefpass- und Bandpass-Signale
Aufgabe 4.2: Rechteckförmige Spektren
Aufgabe 4.2Z: Multiplikation mit Sinussignal