Informationstheorie/Differentielle Entropie: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (45 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
|Nächste Seite=AWGN–Kanalkapazität bei wertkontinuierlichem Eingang | |Nächste Seite=AWGN–Kanalkapazität bei wertkontinuierlichem Eingang | ||
}} | }} | ||
| + | |||
| + | == # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL # == | ||
| + | <br> | ||
| + | Im letzten Kapitel dieses Buches werden die bisher für den wertdiskreten Fall definierten informationstheoretischen Größen derart adaptiert, dass sie auch auf wertkontinuierliche Zufallsgrößen angewandt werden können. | ||
| + | *Aus der Entropie $H(X)$ für die wertdiskrete Zufallsgröße $X$ wird so zum Beispiel im wertkontinuierlichen Fall die »differentielle Entropie« $h(X)$. | ||
| + | *Während $H(X)$ die »Unsicherheit« hinsichtlich der diskreten Zufallsgröße $X$ angibt, kann man im kontinuierlichen Fall $h(X)$ nicht in gleicher Weise interpretieren. | ||
| + | |||
| + | |||
| + | Viele der im dritten Kapitel »Information zwischen zwei wertdiskreten Zufallsgrößen« ⇒ siehe [[Informationstheorie|Inhaltsverzeichnis]] für die herkömmliche Entropie hergeleiteten Zusammenhänge gelten auch für die differentielle Entropie. So kann auch für wertkontinuierliche Zufallsgrößen $X$ und $Y$ die differentielle Verbundentropie $h(XY)$ angegeben werden und ebenso die beiden bedingten differentiellen Entropien $h(Y|X)$ und $h(X|Y)$. | ||
| + | |||
| + | |||
| + | Im Einzelnen werden in diesem Hauptkapitel behandelt: | ||
| + | *die »Besonderheiten wertkontinuierlicher Zufallsgrößen«, | ||
| + | *die Definition und Berechnung der »differentiellen Entropie« sowie deren Eigenschaften, | ||
| + | *die »Transinformation« zwischen zwei wertkontinuierlichen Zufallsgrößen, | ||
| + | *die »Kapazität des AWGN–Kanals« und mehrerer solcher paralleler Gaußkanäle, | ||
| + | *das »Kanalcodierungstheorem«, eines der „Highlights” der Shannonschen Informationstheorie, | ||
| + | *die »AWGN–Kanalkapazität für wertdiskrete Eingangssinale« (BPSK, QPSK). | ||
| + | |||
| + | |||
| + | |||
==Eigenschaften wertkontinuierlicher Zufallsgrößen== | ==Eigenschaften wertkontinuierlicher Zufallsgrößen== | ||
| + | <br> | ||
| + | Bisher wurden stets wertdiskrete Zufallsgrößen der Form $X = \{x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm} , x_μ, \text{...} ,\ x_M\}$ betrachtet, die aus informationstheoretischer Sicht vollständig durch ihre [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Wahrscheinlichkeitsfunktion_und_Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsfunktion]] (englisch: "Probability Mass Function", PMF) $P_X(X)$ charakterisiert werden: | ||
| + | |||
| + | :$$P_X(X) = \big [ \hspace{0.1cm} | ||
| + | p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] | ||
| + | \hspace{0.3cm}{\rm mit} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | Eine '''wertkontinuierliche Zufallsgröße''' kann dagegen – zumindest in endlichen Intervallen – jeden beliebigen Wert annehmen: | |
| − | + | * Aufgrund des nicht abzählbaren Wertevorrats ist in diesem Fall die Beschreibung durch eine Wahrscheinlichkeitsfunktion nicht möglich oder zumindest nicht sinnvoll: | |
| − | Eine '''wertkontinuierliche Zufallsgröße''' kann dagegen – zumindest in endlichen Intervallen – jeden beliebigen Wert annehmen | + | *Es ergäbe sich nämlich der Symbolumfang $M \to ∞$ sowie die Wahrscheinlichkeiten $p_1 \to 0$, $p_2 \to 0$, usw. |
| + | Man verwendet zur Beschreibung wertkontinuierlicher Zufallsgrößen gemäß den Definitionen im Buch [[Stochastische Signaltheorie]] gleichermaßen: | ||
| − | + | [[Datei:P_ID2850__Inf_T_4_1_S1b.png|right|frame|WDF und VTF einer wertkontinuierlichen Zufallsgröße]] | |
| − | |||
| − | + | * die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion_(WDF)|Wahrscheinlichkeitsdichtefunktion]] (WDF, englisch: "Probability Density Function", PDF): | |
| − | |||
| − | In Worten: Der WDF–Wert bei $x_0$ gibt die Wahrscheinlichkeit $p_{Δx}$ an, dass | + | :$$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$ |
| − | * Mittelwert (Moment erster Ordnung, englisch: | + | |
| + | :In Worten: Der WDF–Wert bei $x_0$ gibt die Wahrscheinlichkeit $p_{Δx}$ an, dass $X$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_0$ liegt, dividiert durch $Δx$; (beachten Sie die Einträge in nebenstehender Grafik); | ||
| + | *den [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Momentenberechnung_als_Scharmittelwert|Mittelwert]] (Moment erster Ordnung, englisch: "Mean Value" bzw. "Expected Value"): | ||
| − | *Varianz (Zentralmoment zweiter Ordnung, englisch: | + | :$$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x |
| + | \hspace{0.05cm};$$ | ||
| + | |||
| + | *die [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente|Varianz]] (Zentralmoment zweiter Ordnung, englisch: "Variance"): | ||
| − | *Verteilungsfunktion (VTF, englisch: | + | :$$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x |
| + | \hspace{0.05cm};$$ | ||
| + | |||
| + | *die [[Stochastische_Signaltheorie/Verteilungsfunktion_(VTF)|Verteilungsfunktion]] (VTF, englisch: "Cumulative Distribution Function", CDF): | ||
| − | + | :$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | |
| + | \hspace{0.2cm} = \hspace{0.2cm} | ||
| + | {\rm Pr}(X \le x)\hspace{0.05cm}.$$ | ||
| − | + | Beachten Sie, dass sowohl die WDF–Fläche als auch der VTF–Endwert stets gleich $1$ sind. | |
| − | Die ''Wahrscheinlichkeitsdichtefunktion'' der Gleichverteilung hat den | + | {{BlaueBox|TEXT= |
| + | $\text{Nomenklaturhinweise zu WDF und VTF:}$ | ||
| + | |||
| + | Wir verwenden in diesem Kapitel für eine '''Wahrscheinlichkeitsdichtefunktion''' $\rm (WDF)$ die in der Literatur häufig verwendete Darstellungsform $f_X(x)$, wobei gilt: | ||
| + | *$X$ bezeichnet die (wertdiskrete oder wertkontinuierliche) Zufallsgröße, | ||
| + | *$x$ ist eine mögliche Realisierung von $X$ ⇒ $x ∈ X$. | ||
| + | |||
| + | |||
| + | Entsprechend bezeichnen wir die '''Verteilungsfunktion''' $\rm (VTF)$ der Zufallsgröße $X$ mit $F_X(x)$ entsprechend folgender Definition: | ||
| + | :$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | ||
| + | \hspace{0.2cm} = \hspace{0.2cm} | ||
| + | {\rm Pr}(X \le x)\hspace{0.05cm}.$$ | ||
| + | |||
| + | In anderen $\rm LNTwww$–Büchern schreiben wir oft, um nicht für eine Variable zwei Zeichen zu verbrauchen: | ||
| + | *Für die WDF $f_x(x)$ ⇒ keine Unterscheidung zwischen Zufallsgröße und Realisiering, und | ||
| + | *für die VTF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ hier benötigt man auf jeden Fall eine zweite Variable. | ||
| + | |||
| + | |||
| + | Wir bitten, diese formale Ungenauigkeit zu entschuldigen.}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Wir betrachten nun mit der Gleichverteilung einen wichtigen Sonderfall. | ||
| + | [[Datei:P_ID2849__Inf_T_4_1_S1.png|right|frame|Zwei Analogsignale als Beispiele für wertkontinuierliche Zufallsgrößen]] | ||
| + | *Die Grafik zeigt den Verlauf zweier gleichverteilter Größen, die alle Werte zwischen $1$ und $5$ $($Mittelwert $m_1 = 3)$ mit gleicher Wahrscheinlichkeit annehmen kann. | ||
| + | *Links ist das Ergebnis eines Zufallsprozesses dargestellt, rechts ein deterministisches Signal („Sägezahn”) mit gleicher Amplitudenverteilung. | ||
| + | |||
| + | [[Datei:P_ID2870__Inf_A_4_1a.png|right|frame|WDF und VTF einer gleichverteilten Zufallsgröße]] | ||
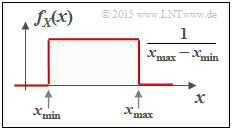
| + | <br>Die '''Wahrscheinlichkeitsdichtefunktion''' der Gleichverteilung hat den in der zweiten Grafik oben skizzierten Verlauf: | ||
| + | :$$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ \end{array} | ||
| + | \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.1cm}{\rm und}\hspace{0.1cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$ | ||
| + | |||
| − | Es ergeben sich hier für den Mittelwert $m_1 | + | Es ergeben sich hier für den Mittelwert $m_1 ={\rm E}\big[X\big]$ und die Varianz $σ^2={\rm E}\big[(X – m_1)^2\big]$ folgende Gleichungen: |
| − | Unten dargestellt ist die ''Verteilungsfunktion'' (VTF): | + | :$$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, $$ |
| + | :$$\sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Unten dargestellt ist die '''Verteilungsfunktion''' (VTF): | ||
| − | Diese ist für $x ≤ x_{\rm min}$ identisch | + | :$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi |
| − | Die Wahrscheinlichkeit, dass die Zufallgröße $X$ einen Wert zwischen 3 und 4 annimmt, kann sowohl aus der WDF als auch aus der VTF ermittelt werden: | + | \hspace{0.2cm} = \hspace{0.2cm} |
| − | + | {\rm Pr}(X \le x)\hspace{0.05cm}.$$ | |
| + | |||
| + | *Diese ist für $x ≤ x_{\rm min}$ identisch Null, steigt danach linear an und erreicht bei $x = x_{\rm max}$ den VTF–Endwert $1$. | ||
| + | *Die Wahrscheinlichkeit, dass die Zufallgröße $X$ einen Wert zwischen $3$ und $4$ annimmt, kann sowohl aus der WDF als auch aus der VTF ermittelt werden: | ||
| + | :$${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$ | ||
| + | |||
Weiterhin ist zu beachten: | Weiterhin ist zu beachten: | ||
| − | *Das Ergebnis $X | + | *Das Ergebnis $X = 0$ ist bei dieser Zufallsgröße ausgeschlossen ⇒ ${\rm Pr}(X = 0) = 0$. |
| − | *Das Ergebnis $X | + | *Das Ergebnis $X = 4$ ist dagegen durchaus möglich. Trotzdem gilt auch hier ${\rm Pr}(X = 4) = 0$.}} |
==Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung == | ==Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung == | ||
| + | <br> | ||
| + | Wir betrachten nun eine wertkontinuierliche Zufallsgröße $X$ im Bereich von $0 \le x \le 1$. | ||
| + | *Wir quantisieren die Zufallsgröße $X$, um die bisherige Entropieberechnung weiter anwenden zu können. Die so entstehende diskrete (quantisierte) Größe nennen wir $Z$. | ||
| + | *Die Quantisierungsstufenzahl sei $M$, so dass jedes Intervall $μ$ bei der vorliegenden WDF die Breite ${\it Δ} = 1/M$ aufweist. Die Intervallmitten bezeichnen wir mit $x_μ$. | ||
| + | *Die Wahrscheinlichkeit $p_μ = {\rm Pr}(Z = z_μ)$ bezüglich $Z$ ist gleich der Wahrscheinlichkeit, dass $X$ einen Wert zwischen $x_μ - {\it Δ}/2$ und $x_μ + {\it Δ}/2$ besitzt. | ||
| + | *Zunächst setzen wir $M = 2$ und verdoppeln anschließend diesen Wert in jeder Iteration. Dadurch wird die Quantisierung zunehmend feiner. | ||
| + | *Im $n$–ten Versuch gilt dann $M = 2^n$ und ${\it Δ} =2^{–n}$. | ||
| + | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 2:}$ Die Grafik zeigt die Ergebnisse der ersten drei Versuche für eine unsymmetrisch–dreieckförmige WDF $($zwischen $0$ und $1)$: | |
| − | * | + | [[Datei:P_ID2851__Inf_T_4_1_S2.png|right|frame|Entropiebestimmung der Dreieck–WDF nach Quantisierung]] |
| − | * | + | * $n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$ $H(Z) = 0.811\ \rm bit,$ |
| − | * | + | * $n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$ $H(Z) = 1.749\ \rm bit,$ |
| + | * $n = 3 \ ⇒ \ M = 8 \ ⇒ \ {\it Δ} = 1/8\text{:}$ $H(Z) = 2.729\ \rm bit.$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Zudem können der Grafik noch folgende Größen entnommen werden, zum Beispiel für $Δ = 1/8$: | + | Zudem können der Grafik noch folgende Größen entnommen werden, zum Beispiel für ${\it Δ} = 1/8$: |
| − | *Die Intervallmitten liegen bei $x_1 = 1/16, x_2 = 3/16, ... , x_8 = 15/16 | + | *Die Intervallmitten liegen bei |
| − | + | :$$x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 $$ | |
| − | + | :$$ ⇒ \ x_μ = {\it Δ} · (μ - 1/2).$$ | |
| − | { | + | *Die Intervallflächen ergeben sich zu |
| + | :$$p_μ = {\it Δ} · f_X(x_μ) ⇒ p_8 = 1/8 · (7/8+1)/2 = 15/64.$$ | ||
| + | *Damit lautet die $\rm PMF$ der quantisierten Zufallsgröße $Z$: | ||
| + | :$$P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64).$$}} | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ | ||
Die Ergebnisse dieses Experiments interpretieren wir wie folgt: | Die Ergebnisse dieses Experiments interpretieren wir wie folgt: | ||
| − | *Die Entropie $H(Z)$ | + | *Die Entropie $H(Z)$ wird mit steigendem $M$ immer größer. |
| − | *Der Grenzwert von $H(Z)$ für $M | + | *Der Grenzwert von $H(Z)$ für $M \to ∞ \ ⇒ \ {\it Δ} → 0$ ist unendlich. |
| − | *Damit ist auch die Entropie $H(X)$ der wertkontinuierlichen Zufallsgröße $X$ unendlich groß. | + | *Damit ist auch die Entropie $H(X)$ der wertkontinuierlichen Zufallsgröße $X$ unendlich groß. |
| − | *Daraus folgt: Die bisherige Entropie–Definition versagt | + | *Daraus folgt: '''Die bisherige Entropie–Definition versagt bei wertkontinuierlichen Zufallsgrößen'''.}} |
Zur Verifizierung unseres empirischen Ergebnisses gehen wir von folgender Gleichung aus: | Zur Verifizierung unseres empirischen Ergebnisses gehen wir von folgender Gleichung aus: | ||
| − | + | :$$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$ | |
| + | |||
| + | Wir spalten nun $H(Z) = S_1 + S_2$ in zwei Summanden auf: | ||
| − | Die Näherung $S_1 ≈ | + | :$$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ |
| + | S_2 & = \hspace{0.05cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x_{\mu} ) } \cdot {\it \Delta} \hspace{0.2cm}\approx | ||
| + | \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$ | ||
| + | |||
| + | *Die Näherung $S_1 ≈ -\log_2 {\it Δ}$ gilt exakt nur im Grenzfall ${\it Δ} → 0$. | ||
| + | *Die angegebene Näherung für $S_2$ gilt ebenfalls nur für kleine ${\it Δ} → {\rm d}x$, so dass man die Summe durch das Integral ersetzen sollte. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Verallgemeinerung:}$ | ||
| + | Nähert man die wertkontinuierliche Zufallsgröße $X$ mit der WDF $f_X(x)$ durch eine wertdiskrete Zufallsgröße $Z$ an, indem man eine (feine) Quantisierung mit der Intervallbreite ${\it Δ}$ durchführt, so erhält man für die Entropie der Zufallsgröße $Z$: | ||
| + | :$$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ | ||
| + | \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$ | ||
| − | + | Das Integral beschreibt die [[Informationstheorie/Differentielle_Entropie#Definition_und_Eigenschaften_der_differentiellen_Entropie|differentielle Entropie]] $h(X)$ der wertkontinuierlichen Zufallsgröße $X$. | |
| − | + | ||
| + | Für den Sonderfall ${\it Δ} = 1/M = 2^{-n}$ kann die obige Gleichung auch wie folgt geschrieben werden: | ||
| − | + | :$$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$ | |
| − | + | ||
| − | *Im Grenzfall $Δ → 0 | + | *Im Grenzfall ${\it Δ} → 0 \ ⇒ \ M → ∞ \ ⇒ \ n → ∞$ ist auch die Entropie der wertkontinuierlichen Zufallsgröße unendlich groß: $H(X) → ∞$. |
| − | * | + | *Für jedes $n$ ist die Gleichung $H(Z) = n$ nur eine Näherung, wobei die differentielle Entropie $h(X)$ der kontinuierlichen Größe als Korrekturfaktor dient.}} |
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ Wir betrachten wie im $\text{Beispiel 2}$ eine unsymmetrisch–dreieckförmige WDF. Deren differentielle Entropie ergibt sich, wie in [[Aufgaben:4.2_Dreieckförmige_WDF| Aufgabe 4.2]] berechnet, zu | ||
| + | [[Datei:P_ID2852__Inf_T_4_1_S2c.png|right|frame|Entropie der unsymmetrisch–dreieckförmigen WDF nach Quantisierung ]] | ||
| + | :$$h(X) = \hspace{0.05cm}-0.279 \ \rm bit.$$ | ||
| − | + | * In der Tabelle ist die Entropie $H(Z)$ der mit $n$ Bit quantisierten Größe $Z$ angegeben. | |
| − | + | *Man erkennt schon für $n = 3$ eine gute Übereinstimmung zwischen der Näherung (untere Zeile) und der exakten Berechnung (Zeile 2). | |
| − | |||
| − | + | *Für $n = 10$ wird die Näherung noch besser mit der exakten Berechnung (die extrem aufwändig ist) übereinstimmen. | |
| + | }} | ||
==Definition und Eigenschaften der differentiellen Entropie == | ==Definition und Eigenschaften der differentiellen Entropie == | ||
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Verallgemeinerung:}$ | ||
| + | Die '''differentielle Entropie''' $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ lautet mit der Wahrscheinlichkeitsdichtefunktion $f_X(x)$: | ||
| + | |||
| + | :$$h(X) = | ||
| + | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x | ||
| + | \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
Hinzugefügt werden muss jeweils eine Pseudo–Einheit: | Hinzugefügt werden muss jeweils eine Pseudo–Einheit: | ||
| − | *„nat” bei Verwendung von „ln” ⇒ natürlicher Logarithmus, | + | *„nat” bei Verwendung von „ln” ⇒ natürlicher Logarithmus, |
| − | *„bit” bei Verwendung von | + | *„bit” bei Verwendung von „log<sub>2</sub>” ⇒ Logarithmus dualis.}} |
| − | |||
| + | Während für die (herkömmliche) Entropie einer wertdiskreten Zufallsgröße $X$ stets $H(X) ≥ 0$ gilt, kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße auch negativ sein. Daraus ist bereits ersichtlich, dass $h(X)$ im Gegensatz zu $H(X)$ nicht als „Unsicherheit” interpretiert werden kann. | ||
| − | + | [[Datei:P_ID2854__Inf_T_4_1_S3a_neu.png|right|frame|WDF einer gleichverteilten Zufallsgröße]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ | ||
| + | Die obere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ einer zwischen $x_{\rm min}$ und $x_{\rm max}$ gleichverteilten Zufallsgröße $X$. Für deren differentielle Entropie erhält man in „nat”: | ||
| + | |||
| + | :$$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = | ||
| + | {\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$ | ||
| + | Die Gleichung für die differentielle Entropie in „bit” lautet: | ||
| + | :$$h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big].$$ | ||
| − | + | [[Datei:P_ID2855__Inf_T_4_1_S3b_neu.png|left|frame|$h(X)$ für verschiedene rechteckförmige Dichtefunktionen]] | |
| − | Die Grafik zeigt die | + | <br><br><br><br>Die linke Grafik zeigt anhand einiger Beispiele die numerische Auswertung des obigen Ergebnisses. |
| − | + | }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Interpretation:}$ | ||
| + | Aus den sechs Skizzen im letzten Beispiel lassen sich wichtige Eigenschaften der differentiellen Entropie $h(X)$ ablesen: | ||
| + | *Die differentielle Entropie wird durch eine WDF–Verschiebung $($um $k)$ nicht verändert: | ||
| + | :$$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$ | ||
| + | |||
| + | * $h(X)$ ändert sich durch Stauchung/Spreizung der WDF um den Faktor $k ≠ 0$ wie folgt: | ||
| + | :$$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | \text{Beispielsweise gilt} \ \ h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = | ||
| + | {\rm log}_2 \hspace{0.05cm} (2A) | ||
| + | \hspace{0.05cm}.$$}} | ||
| + | |||
| − | + | Des Weiteren gelten viele der im Kapitel [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|Verschiedene Entropien zweidimensionaler Zufallsgrößen]] für den wertdiskreten Fall hergeleitete Gleichungen auch für wertkontinuierliche Zufallsgrößen. | |
| − | + | Aus der folgenden Zusammenstellung erkennt man, dass oft nur das (große) $H$ durch ein (kleines) $h$ sowie die Wahrscheinlichkeitsfunktion (englische Abkürzung: $\rm PMF)$ durch die entsprechende Wahrscheinlichkeitsdichtefunktion $\rm (PDF$ bzw. $\rm WDF)$ zu ersetzen ist. | |
| − | * '''Bedingte differentielle Entropie''' (englisch: | + | * '''Bedingte differentielle Entropie''' (englisch: "Conditional Differential Entropy"): |
| − | * '''Differentielle Verbundentropie''' (englisch: | + | :$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} |
| + | \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} | ||
| + | \hspace{0.05cm}$$ | ||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm}h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | ||
| + | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| + | |||
| + | * '''Differentielle Verbundentropie''' (englisch: "Joint Differential Entropy"): | ||
| − | * '''Kettenregel''' der differentiellen Entropie: | + | :$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} |
| + | \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ P_{XY}(x, y)} \hspace{0.05cm}$$ | ||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm}h(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{f_{XY}(X, Y)}\right ] =\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | ||
| + | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_{XY}(x, y) } | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| + | |||
| + | * '''Kettenregel''' der differentiellen Entropie: | ||
| − | * '''Kullback–Leibler–Distanz''' zwischen den Zufallsgrößen $X$ und $Y$: | + | :$$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} |
| + | H(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) | ||
| + | \le \sum_{i = 1}^{n} | ||
| + | H(X_i) | ||
| + | \hspace{0.05cm}$$ | ||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm} | ||
| + | h(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} | ||
| + | h(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) | ||
| + | \le \sum_{i = 1}^{n} | ||
| + | h(X_i) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | * '''Kullback–Leibler–Distanz''' zwischen den Zufallsgrößen $X$ und $Y$: | ||
| + | :$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} | ||
| + | P_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)} | ||
| + | \ge 0$$ | ||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm}D(f_X \hspace{0.05cm} || \hspace{0.05cm}f_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{f_X(X)}{f_Y(X)}\right ] \hspace{0.2cm}= \hspace{-0.4cm}\int\limits_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} | ||
| + | f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{f_X(x)}{f_Y(x)} \hspace{0.15cm}{\rm d}x \ge 0 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
==Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen == | ==Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen == | ||
| + | <br> | ||
| + | [[Datei:P_ID2867__Inf_A_4_1.png|right|frame|Differentielle Entropie spitzenwertbegrenzter Zufallsgrößen]] | ||
| + | Die Tabelle zeigt die Ergebnisse hinsichtlich der differentiellen Entropie für drei beispielhafte Wahrscheinlichkeitsdichtefunktionen $f_X(x)$. Diese sind alle spitzenwertbegrenzt, das heißt, es gilt jeweils $|X| ≤ A$. | ||
| + | |||
| + | *Bei »Spitzenwertbegrenzung« kann man die differentielle Entropie stets wie folgt darstellen: | ||
| + | |||
| + | :$$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$ | ||
| + | |||
| + | *Anzufügen ist bei Verwendung von $\ln$ die Pseudo–Einheit „nat” und bei Verwendung von $\log_2$ die Pseudo–Einheit „bit”. | ||
| + | *Die Konstante ${\it \Gamma}_{\rm A}$ hängt allein von der WDF-Form ab und gilt nur für »Spitzenwertbegrenzung« ⇒ »$\rm A$mplitudenbegrenzung«. | ||
| + | *Eine Gleichverteilung im Bereich $|X| ≤ 1$ liefert $h(X) = 1$ bit, eine zweite im Bereich $|Y| ≤ 4$ dagegen zu $h(Y) = 3$ bit. | ||
| + | |||
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Theorem:}$ | ||
| + | Unter der Nebenbedingung '''Spitzenwertbegrenzung''' (englisch: "Peak Constraint") ⇒ also WDF $f_X(x) = 0$ für $ \vert x \vert > A$ – führt die '''Gleichverteilung''' zur maximalen differentiellen Entropie: | ||
| + | :$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$ | ||
| + | Hier ist die geeignete Kenngröße ${\it \Gamma}_{\rm A} = 2$ maximal. | ||
| + | Sie finden den [[Informationstheorie/Differentielle_Entropie#Beweis:_Maximale_differentielle_Entropie_bei_Spitzenwertbegrenzung|Beweis]] am Ende dieses Kapitels.}} | ||
| + | |||
| + | |||
| + | Das Theorem bedeutet gleichzeitig, dass bei jeder anderen spitzenwertbegrenzten WDF (außer der Gleichverteilung) der Kennparameter ${\it \Gamma}_{\rm A} < 2$ ist. | ||
| + | *Für die symmetrische Dreieckverteilung ergibt sich nach obiger Tabelle ${\it \Gamma}_{\rm A} = \sqrt{\rm e} ≈ 1.649$. | ||
| + | *Beim einseitigen Dreieck $($zwischen $0$ und $A)$ ist demgegenüber ${\it \Gamma}_{\rm A}$ nur halb so groß. | ||
| + | *Auch für jedes andere Dreieck $($absolute Breite $A$, Spitze beliebig zwischen $0$ und $A)$ gilt ${\it \Gamma}_{\rm A} ≈ 0.824$. | ||
| + | |||
| + | |||
| + | Die jeweils zweite $h(X)$–Angabe und die Kenngröße ${\it \Gamma}_{\rm L}$ eignet sich dagegen für den Vergleich von Zufallsgrößen bei Leistungsbegrenzung, der im nächsten Abschnitt behandelt wird. Unter dieser Nebenbedingung ist zum Beispiel die symmetrische Dreieckverteilung $({\it \Gamma}_{\rm L} ≈ 16.31)$ besser als die Gleichverteilung ${\it \Gamma}_{\rm L} = 12)$. | ||
| + | |||
| + | |||
| + | ==Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen == | ||
| + | <br> | ||
| + | [[Datei:P_ID2873__Inf_T_4_1_S5a_neu.png|right|frame|Differentielle Entropie leistungsbegrenzter Zufallsgrößen]] | ||
| + | |||
| + | In der folgenden Tabelle sind die differentiellen Entropien $h(X)$ für drei beispielhafte Dichtefunktionen $f_X(x)$ ohne Begrenzung zu entnehmen, die durch entsprechende Parameterwahl alle die gleiche Varianz $σ^2 = {\rm E}\big[|X -m_x|^2 \big]$ aufweisen. Berücksichtigt sind: | ||
| + | |||
| + | *die [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen|Gaußverteilung]]'', | ||
| + | *die [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen#Zweiseitige_Exponentialverteilung_.E2.80.93_Laplaceverteilung|Laplaceverteilung]] ⇒ eine zweiseitige Exponentialverteilung, | ||
| + | *die (einseitige) [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen#Einseitige_Exponentialverteilung|Exponentialverteilung]]. | ||
| + | |||
| + | |||
| + | Bei »Leistungsbegrenzung« lässt sich die differentielle Entropie stets wie folgt darstellen: | ||
| + | :$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2).$$ | ||
| + | Das Ergebnis unterscheidet sich nur durch die Pseudo–Einheit | ||
| + | *„nat” bei Verwendung von $\ln$ bzw. | ||
| + | *„bit” bei Verwendung vo n $\log_2$. | ||
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Theorem:}$ | ||
| + | Unter der Nebenbedingung der '''Leistungsbegrenzung''' (englisch: "Power Constraint") führt die '''Gaußverteilung''', | ||
| + | :$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm e}^{ | ||
| + | - \hspace{0.05cm}{(x - m_1)^2}/(2 \sigma^2)},$$ | ||
| + | unabhängig vom Mittelwert $m_1$ zur maximalen differentiellen Entropie: | ||
| + | :$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$ | ||
| + | Sie finden den [[Informationstheorie/Differentielle_Entropie#Beweis:_Maximale_differentielle_Entropie_bei_Leistungsbegrenzung|Beweis]] am Ende dieses Kapitels.}} | ||
| + | |||
| + | |||
| + | Diese Aussage bedeutet gleichzeitig, dass für jede andere WDF als die Gaußverteilung die Kenngröße ${\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08$ sein wird. | ||
| + | |||
| + | Beispielsweise ergibt sich der Kennwert | ||
| + | *für die Dreieckverteilung zu ${\it \Gamma}_{\rm L} = 6{\rm e} ≈ 16.31$, | ||
| + | *für die Laplaceverteilung zu ${\it \Gamma}_{\rm L} = 2{\rm e}^2 ≈ 14.78$, und | ||
| + | *für die Gleichverteilung zu ${\it \Gamma}_{\rm L} = 12$ . | ||
| + | |||
| + | ==Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung== | ||
| + | <br> | ||
| + | Unter der Nebenbedingung der »Spitzenwertbegrenzung« ⇒ $|X| ≤ A$ gilt für die differentielle Entropie: | ||
| + | :$$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | ||
| + | |||
| + | Von allen möglichen Wahrscheinlichkeitsdichtefunktionen $f_X(x)$, die die Bedingung | ||
| + | :$$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$ | ||
| + | erfüllen, ist nun diejenige Funktion $g_X(x)$ gesucht, die zur maximalen differentiellen Entropie $h(X)$ führt. | ||
| + | |||
| + | Zur Herleitung benutzen wir das Verfahren der [https://de.wikipedia.org/wiki/Lagrange-Multiplikator Lagrange–Multiplikatoren]: | ||
| + | *Wir definieren die Lagrange–Kenngröße $L$ in der Weise, dass darin sowohl $h(X)$ als auch die Nebenbedingung $|X| ≤ A$ enthalten sind: | ||
| + | :$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} | ||
| + | \lambda \cdot | ||
| + | \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *Wir setzen allgemein $f_X(x) = g_X(x) + ε · ε_X(x)$, wobei $ε_X(x)$ eine beliebige Funktion darstellt, mit der Einschränkung, dass die WDF–Fläche gleich $1$ sein muss. Damit erhalten wir: | ||
| + | :$$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm}\big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x)\big ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot | ||
| + | \int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x | ||
| + | \hspace{0.05cm}.\end{align*}$$ | ||
| + | *Die bestmögliche Funktion ergibt sich dann, wenn es für $ε = 0$ eine stationäre Lösung gibt: | ||
| + | :$$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot | ||
| + | \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *Diese Bedingungsgleichung ist unabhängig von $ε_X$ nur dann zu erfüllen, wenn gilt: | ||
| + | :$${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} | ||
| + | \forall x \in \big[-A, +A \big]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} | ||
| + | g_X(x) = {\rm const.}\hspace{0.4cm} | ||
| + | \forall x \in \big [-A, +A \big]\hspace{0.05cm}.$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Resümee bei Spitzenwertbegrenzung:}$ | ||
| + | |||
| + | Die maximale differentielle Entropie ergibt sich unter der Nebenbedingung $ \vert X \vert ≤ A$ für die '''Gleichverteilung''' (englisch: "Uniform PDF"): | ||
| + | :$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Jede andere Zufallsgröße mit der WDF–Eigenschaft $f_X(\vert x \vert > A) = 0$ führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch den Parameter ${\it \Gamma}_{\rm A} < 2$.}} | ||
| + | |||
| + | ==Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung== | ||
| + | <br> | ||
| + | Vorneweg zur Begriffserklärung: | ||
| + | *Eigentlich wird nicht die Leistung ⇒ das [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Momentenberechnung_als_Scharmittelwert|zweite Moment]] $m_2$ begrenzt, sondern das [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente|zweite Zentralmoment]] ⇒ Varianz $μ_2 = σ^2$. | ||
| + | *Gesucht wird also nun die maximale differentielle Entropie unter der Nebenbedingung ${\rm E}\big[|X – m_1|^2 \big] ≤ σ^2$. | ||
| + | *Das $≤$–Zeichen dürfen wir hierbei durch das Gleichheitszeichen ersetzen. | ||
| + | |||
| + | |||
| + | Lassen wir nur mittelwertfreie Zufallsgrößen zu, so umgehen wir das Problem. Damit lautet der [https://de.wikipedia.org/wiki/Lagrange-Multiplikator Lagrange-Multiplikator]: | ||
| + | |||
| + | :$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} | ||
| + | \lambda_1 \cdot | ||
| + | \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \hspace{0.1cm}{\rm d}x | ||
| + | \hspace{0.1cm}+ \hspace{0.1cm} | ||
| + | \lambda_2 \cdot | ||
| + | \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | ||
| + | |||
| + | Nach ähnlichem Vorgehen wie beim [[Informationstheorie/Differentielle_Entropie#Beweis:_Maximale_differentielle_Entropie_bei_Spitzenwertbegrenzung|Beweis für Spitzenwertbegrenzung]] zeigt sich, dass die „bestmögliche” Funktion $g_X(x) \sim {\rm e}^{–λ_2\hspace{0.05cm} · \hspace{0.05cm} x^2}$ sein muss ⇒ [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilung]]: | ||
| + | |||
| + | :$$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ | ||
| + | - \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$ | ||
| − | + | Wir verwenden hier aber für den expliziten Beweis die [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Relative_Entropie_.E2.80.93_Kullback.E2.80.93Leibler.E2.80.93Distanz|Kullback–Leibler–Distanz]] zwischen einer geeigneten allgemeinen WDF $f_X(x)$ und der Gauß–WDF $g_X(x)$: | |
| + | |||
| + | :$$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} | ||
| + | f_X(x) \cdot {\rm ln} \hspace{0.1cm} \frac{f_X(x)}{g_X(x)} \hspace{0.1cm}{\rm d}x = -h(X) - I_2\hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm}I_2 = \int_{-\infty}^{+\infty} \hspace{0.02cm} | ||
| + | f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | ||
| − | + | Zur Vereinfachung ist hier der natürliche Logarithmus ⇒ $\ln$ verwendet. Damit erhalten wir für das zweite Integral: | |
| − | + | :$$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x | |
| − | + | \hspace{0.3cm}- \hspace{0.3cm} | |
| − | + | \frac{1}{2\sigma^2} \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{0.02cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x | |
| + | \hspace{0.05cm}.$$ | ||
| − | + | Das erste Integral ist definitionsgemäß gleich $1$ und das zweite Integral ergibt $σ^2$: | |
| − | |||
| − | + | :$$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$ | |
| − | {{ | + | :$$\Rightarrow\hspace{0.3cm} D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = -h(X) - I_2 = |
| + | -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Da auch bei wertkontinuierlichen Zufallsgrößen die Kullback–Leibler–Distanz stets $\ge 0$ ist, erhält man nach Verallgemeinerung („ln” ⇒ „log”): | ||
| + | |||
| + | :$$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Das Gleichzeichen gilt nur, wenn die Zufallsgröße $X$ gaußverteilt ist. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Resümee bei Leistungsbegrenzung:}$ | ||
| + | |||
| + | Die maximale differentielle Entropie ergibt sich unter der Bedingung ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ unabhängig von $m_1$ für die '''Gaußverteilung''' (englisch: "Gaussian PDF"): | ||
| + | :$$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = | ||
| + | {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | Jede andere wertkontinuierliche Zufallsgröße $X$ mit Varianz ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ führt zu einem kleineren Wert, gekennzeichnet durch die Kenngröße ${\it \Gamma}_{\rm L} < 2πe$. }} | ||
| + | |||
| + | |||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:4.1 WDF, VTF und Wahrscheinlichkeit|Aufgabe 4.1: WDF, VTF und Wahrscheinlichkeit]] | ||
| + | |||
| + | [[Aufgaben:4.1Z Momentenberechnung|Aufgabe 4.1Z: Momentenberechnung]] | ||
| + | |||
| + | [[Aufgaben:4.2 Dreieckförmige WDF|Aufgabe 4.2: Dreieckförmige WDF]] | ||
| + | |||
| + | [[Aufgaben:4.2Z Gemischte Zufallsgrößen|Aufgabe 4.2Z: Gemischte Zufallsgrößen]] | ||
| + | |||
| + | [[Aufgaben:Aufgabe_4.3:_WDF–Vergleich_bezüglich_differentieller_Entropie|Aufgabe 4.3: WDF–Vergleich bezüglich differentieller Entropie]] | ||
| − | + | [[Aufgaben:4.3Z Exponential– und Laplaceverteilung|Aufgabe 4.3Z: Exponential– und Laplaceverteilung]] | |
| − | + | ||
| − | + | [[Aufgaben:4.4 Herkömmliche Entropie und differenzielle Entropie|Aufgabe 4.4: Herkömmliche Entropie und differenzielle Entropie]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 18. August 2021, 16:59 Uhr
Inhaltsverzeichnis
- 1 # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
- 2 Eigenschaften wertkontinuierlicher Zufallsgrößen
- 3 Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung
- 4 Definition und Eigenschaften der differentiellen Entropie
- 5 Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen
- 6 Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen
- 7 Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung
- 8 Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung
- 9 Aufgaben zum Kapitel
# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
Im letzten Kapitel dieses Buches werden die bisher für den wertdiskreten Fall definierten informationstheoretischen Größen derart adaptiert, dass sie auch auf wertkontinuierliche Zufallsgrößen angewandt werden können.
- Aus der Entropie $H(X)$ für die wertdiskrete Zufallsgröße $X$ wird so zum Beispiel im wertkontinuierlichen Fall die »differentielle Entropie« $h(X)$.
- Während $H(X)$ die »Unsicherheit« hinsichtlich der diskreten Zufallsgröße $X$ angibt, kann man im kontinuierlichen Fall $h(X)$ nicht in gleicher Weise interpretieren.
Viele der im dritten Kapitel »Information zwischen zwei wertdiskreten Zufallsgrößen« ⇒ siehe Inhaltsverzeichnis für die herkömmliche Entropie hergeleiteten Zusammenhänge gelten auch für die differentielle Entropie. So kann auch für wertkontinuierliche Zufallsgrößen $X$ und $Y$ die differentielle Verbundentropie $h(XY)$ angegeben werden und ebenso die beiden bedingten differentiellen Entropien $h(Y|X)$ und $h(X|Y)$.
Im Einzelnen werden in diesem Hauptkapitel behandelt:
- die »Besonderheiten wertkontinuierlicher Zufallsgrößen«,
- die Definition und Berechnung der »differentiellen Entropie« sowie deren Eigenschaften,
- die »Transinformation« zwischen zwei wertkontinuierlichen Zufallsgrößen,
- die »Kapazität des AWGN–Kanals« und mehrerer solcher paralleler Gaußkanäle,
- das »Kanalcodierungstheorem«, eines der „Highlights” der Shannonschen Informationstheorie,
- die »AWGN–Kanalkapazität für wertdiskrete Eingangssinale« (BPSK, QPSK).
Eigenschaften wertkontinuierlicher Zufallsgrößen
Bisher wurden stets wertdiskrete Zufallsgrößen der Form $X = \{x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm} , x_μ, \text{...} ,\ x_M\}$ betrachtet, die aus informationstheoretischer Sicht vollständig durch ihre Wahrscheinlichkeitsfunktion (englisch: "Probability Mass Function", PMF) $P_X(X)$ charakterisiert werden:
- $$P_X(X) = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] \hspace{0.3cm}{\rm mit} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) \hspace{0.05cm}.$$
Eine wertkontinuierliche Zufallsgröße kann dagegen – zumindest in endlichen Intervallen – jeden beliebigen Wert annehmen:
- Aufgrund des nicht abzählbaren Wertevorrats ist in diesem Fall die Beschreibung durch eine Wahrscheinlichkeitsfunktion nicht möglich oder zumindest nicht sinnvoll:
- Es ergäbe sich nämlich der Symbolumfang $M \to ∞$ sowie die Wahrscheinlichkeiten $p_1 \to 0$, $p_2 \to 0$, usw.
Man verwendet zur Beschreibung wertkontinuierlicher Zufallsgrößen gemäß den Definitionen im Buch Stochastische Signaltheorie gleichermaßen:
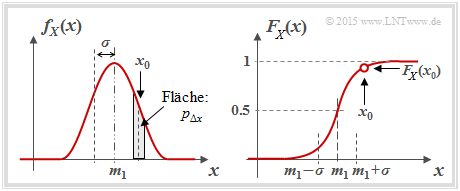
- die Wahrscheinlichkeitsdichtefunktion (WDF, englisch: "Probability Density Function", PDF):
- $$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$
- In Worten: Der WDF–Wert bei $x_0$ gibt die Wahrscheinlichkeit $p_{Δx}$ an, dass $X$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_0$ liegt, dividiert durch $Δx$; (beachten Sie die Einträge in nebenstehender Grafik);
- den Mittelwert (Moment erster Ordnung, englisch: "Mean Value" bzw. "Expected Value"):
- $$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$
- die Varianz (Zentralmoment zweiter Ordnung, englisch: "Variance"):
- $$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$
- die Verteilungsfunktion (VTF, englisch: "Cumulative Distribution Function", CDF):
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
Beachten Sie, dass sowohl die WDF–Fläche als auch der VTF–Endwert stets gleich $1$ sind.
$\text{Nomenklaturhinweise zu WDF und VTF:}$
Wir verwenden in diesem Kapitel für eine Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ die in der Literatur häufig verwendete Darstellungsform $f_X(x)$, wobei gilt:
- $X$ bezeichnet die (wertdiskrete oder wertkontinuierliche) Zufallsgröße,
- $x$ ist eine mögliche Realisierung von $X$ ⇒ $x ∈ X$.
Entsprechend bezeichnen wir die Verteilungsfunktion $\rm (VTF)$ der Zufallsgröße $X$ mit $F_X(x)$ entsprechend folgender Definition:
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
In anderen $\rm LNTwww$–Büchern schreiben wir oft, um nicht für eine Variable zwei Zeichen zu verbrauchen:
- Für die WDF $f_x(x)$ ⇒ keine Unterscheidung zwischen Zufallsgröße und Realisiering, und
- für die VTF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ hier benötigt man auf jeden Fall eine zweite Variable.
Wir bitten, diese formale Ungenauigkeit zu entschuldigen.
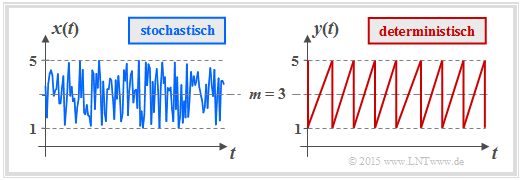
$\text{Beispiel 1:}$ Wir betrachten nun mit der Gleichverteilung einen wichtigen Sonderfall.
- Die Grafik zeigt den Verlauf zweier gleichverteilter Größen, die alle Werte zwischen $1$ und $5$ $($Mittelwert $m_1 = 3)$ mit gleicher Wahrscheinlichkeit annehmen kann.
- Links ist das Ergebnis eines Zufallsprozesses dargestellt, rechts ein deterministisches Signal („Sägezahn”) mit gleicher Amplitudenverteilung.
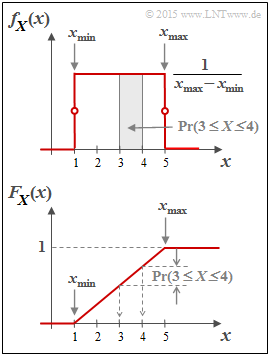
Die Wahrscheinlichkeitsdichtefunktion der Gleichverteilung hat den in der zweiten Grafik oben skizzierten Verlauf:
- $$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ \end{array} \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.1cm}{\rm und}\hspace{0.1cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$
Es ergeben sich hier für den Mittelwert $m_1 ={\rm E}\big[X\big]$ und die Varianz $σ^2={\rm E}\big[(X – m_1)^2\big]$ folgende Gleichungen:
- $$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, $$
- $$\sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$
Unten dargestellt ist die Verteilungsfunktion (VTF):
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
- Diese ist für $x ≤ x_{\rm min}$ identisch Null, steigt danach linear an und erreicht bei $x = x_{\rm max}$ den VTF–Endwert $1$.
- Die Wahrscheinlichkeit, dass die Zufallgröße $X$ einen Wert zwischen $3$ und $4$ annimmt, kann sowohl aus der WDF als auch aus der VTF ermittelt werden:
- $${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$
- $${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$
Weiterhin ist zu beachten:
- Das Ergebnis $X = 0$ ist bei dieser Zufallsgröße ausgeschlossen ⇒ ${\rm Pr}(X = 0) = 0$.
- Das Ergebnis $X = 4$ ist dagegen durchaus möglich. Trotzdem gilt auch hier ${\rm Pr}(X = 4) = 0$.
Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung
Wir betrachten nun eine wertkontinuierliche Zufallsgröße $X$ im Bereich von $0 \le x \le 1$.
- Wir quantisieren die Zufallsgröße $X$, um die bisherige Entropieberechnung weiter anwenden zu können. Die so entstehende diskrete (quantisierte) Größe nennen wir $Z$.
- Die Quantisierungsstufenzahl sei $M$, so dass jedes Intervall $μ$ bei der vorliegenden WDF die Breite ${\it Δ} = 1/M$ aufweist. Die Intervallmitten bezeichnen wir mit $x_μ$.
- Die Wahrscheinlichkeit $p_μ = {\rm Pr}(Z = z_μ)$ bezüglich $Z$ ist gleich der Wahrscheinlichkeit, dass $X$ einen Wert zwischen $x_μ - {\it Δ}/2$ und $x_μ + {\it Δ}/2$ besitzt.
- Zunächst setzen wir $M = 2$ und verdoppeln anschließend diesen Wert in jeder Iteration. Dadurch wird die Quantisierung zunehmend feiner.
- Im $n$–ten Versuch gilt dann $M = 2^n$ und ${\it Δ} =2^{–n}$.
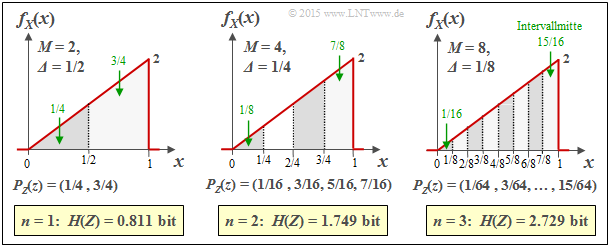
$\text{Beispiel 2:}$ Die Grafik zeigt die Ergebnisse der ersten drei Versuche für eine unsymmetrisch–dreieckförmige WDF $($zwischen $0$ und $1)$:
- $n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$ $H(Z) = 0.811\ \rm bit,$
- $n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$ $H(Z) = 1.749\ \rm bit,$
- $n = 3 \ ⇒ \ M = 8 \ ⇒ \ {\it Δ} = 1/8\text{:}$ $H(Z) = 2.729\ \rm bit.$
Zudem können der Grafik noch folgende Größen entnommen werden, zum Beispiel für ${\it Δ} = 1/8$:
- Die Intervallmitten liegen bei
- $$x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 $$
- $$ ⇒ \ x_μ = {\it Δ} · (μ - 1/2).$$
- Die Intervallflächen ergeben sich zu
- $$p_μ = {\it Δ} · f_X(x_μ) ⇒ p_8 = 1/8 · (7/8+1)/2 = 15/64.$$
- Damit lautet die $\rm PMF$ der quantisierten Zufallsgröße $Z$:
- $$P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64).$$
$\text{Fazit:}$ Die Ergebnisse dieses Experiments interpretieren wir wie folgt:
- Die Entropie $H(Z)$ wird mit steigendem $M$ immer größer.
- Der Grenzwert von $H(Z)$ für $M \to ∞ \ ⇒ \ {\it Δ} → 0$ ist unendlich.
- Damit ist auch die Entropie $H(X)$ der wertkontinuierlichen Zufallsgröße $X$ unendlich groß.
- Daraus folgt: Die bisherige Entropie–Definition versagt bei wertkontinuierlichen Zufallsgrößen.
Zur Verifizierung unseres empirischen Ergebnisses gehen wir von folgender Gleichung aus:
- $$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$
Wir spalten nun $H(Z) = S_1 + S_2$ in zwei Summanden auf:
- $$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ S_2 & = \hspace{0.05cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x_{\mu} ) } \cdot {\it \Delta} \hspace{0.2cm}\approx \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$
- Die Näherung $S_1 ≈ -\log_2 {\it Δ}$ gilt exakt nur im Grenzfall ${\it Δ} → 0$.
- Die angegebene Näherung für $S_2$ gilt ebenfalls nur für kleine ${\it Δ} → {\rm d}x$, so dass man die Summe durch das Integral ersetzen sollte.
$\text{Verallgemeinerung:}$ Nähert man die wertkontinuierliche Zufallsgröße $X$ mit der WDF $f_X(x)$ durch eine wertdiskrete Zufallsgröße $Z$ an, indem man eine (feine) Quantisierung mit der Intervallbreite ${\it Δ}$ durchführt, so erhält man für die Entropie der Zufallsgröße $Z$:
- $$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$
Das Integral beschreibt die differentielle Entropie $h(X)$ der wertkontinuierlichen Zufallsgröße $X$.
Für den Sonderfall ${\it Δ} = 1/M = 2^{-n}$ kann die obige Gleichung auch wie folgt geschrieben werden:
- $$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$
- Im Grenzfall ${\it Δ} → 0 \ ⇒ \ M → ∞ \ ⇒ \ n → ∞$ ist auch die Entropie der wertkontinuierlichen Zufallsgröße unendlich groß: $H(X) → ∞$.
- Für jedes $n$ ist die Gleichung $H(Z) = n$ nur eine Näherung, wobei die differentielle Entropie $h(X)$ der kontinuierlichen Größe als Korrekturfaktor dient.
$\text{Beispiel 3:}$ Wir betrachten wie im $\text{Beispiel 2}$ eine unsymmetrisch–dreieckförmige WDF. Deren differentielle Entropie ergibt sich, wie in Aufgabe 4.2 berechnet, zu
- $$h(X) = \hspace{0.05cm}-0.279 \ \rm bit.$$
- In der Tabelle ist die Entropie $H(Z)$ der mit $n$ Bit quantisierten Größe $Z$ angegeben.
- Man erkennt schon für $n = 3$ eine gute Übereinstimmung zwischen der Näherung (untere Zeile) und der exakten Berechnung (Zeile 2).
- Für $n = 10$ wird die Näherung noch besser mit der exakten Berechnung (die extrem aufwändig ist) übereinstimmen.
Definition und Eigenschaften der differentiellen Entropie
$\text{Verallgemeinerung:}$ Die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ lautet mit der Wahrscheinlichkeitsdichtefunktion $f_X(x)$:
- $$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$$
Hinzugefügt werden muss jeweils eine Pseudo–Einheit:
- „nat” bei Verwendung von „ln” ⇒ natürlicher Logarithmus,
- „bit” bei Verwendung von „log2” ⇒ Logarithmus dualis.
Während für die (herkömmliche) Entropie einer wertdiskreten Zufallsgröße $X$ stets $H(X) ≥ 0$ gilt, kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße auch negativ sein. Daraus ist bereits ersichtlich, dass $h(X)$ im Gegensatz zu $H(X)$ nicht als „Unsicherheit” interpretiert werden kann.
$\text{Beispiel 4:}$ Die obere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ einer zwischen $x_{\rm min}$ und $x_{\rm max}$ gleichverteilten Zufallsgröße $X$. Für deren differentielle Entropie erhält man in „nat”:
- $$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = {\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$
Die Gleichung für die differentielle Entropie in „bit” lautet:
- $$h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big].$$
Die linke Grafik zeigt anhand einiger Beispiele die numerische Auswertung des obigen Ergebnisses.
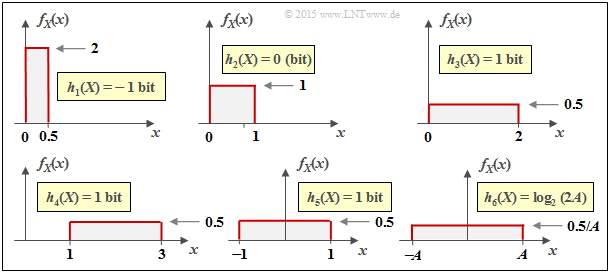
$\text{Interpretation:}$ Aus den sechs Skizzen im letzten Beispiel lassen sich wichtige Eigenschaften der differentiellen Entropie $h(X)$ ablesen:
- Die differentielle Entropie wird durch eine WDF–Verschiebung $($um $k)$ nicht verändert:
- $$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$
- $h(X)$ ändert sich durch Stauchung/Spreizung der WDF um den Faktor $k ≠ 0$ wie folgt:
- $$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = {\rm log}_2 \hspace{0.05cm} (2A) \hspace{0.05cm}.$$
Des Weiteren gelten viele der im Kapitel Verschiedene Entropien zweidimensionaler Zufallsgrößen für den wertdiskreten Fall hergeleitete Gleichungen auch für wertkontinuierliche Zufallsgrößen.
Aus der folgenden Zusammenstellung erkennt man, dass oft nur das (große) $H$ durch ein (kleines) $h$ sowie die Wahrscheinlichkeitsfunktion (englische Abkürzung: $\rm PMF)$ durch die entsprechende Wahrscheinlichkeitsdichtefunktion $\rm (PDF$ bzw. $\rm WDF)$ zu ersetzen ist.
- Bedingte differentielle Entropie (englisch: "Conditional Differential Entropy"):
- $$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm}h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- Differentielle Verbundentropie (englisch: "Joint Differential Entropy"):
- $$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ P_{XY}(x, y)} \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm}h(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{f_{XY}(X, Y)}\right ] =\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_{XY}(x, y) } \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- Kettenregel der differentiellen Entropie:
- $$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} H(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} H(X_i) \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} h(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} h(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} h(X_i) \hspace{0.05cm}.$$
- Kullback–Leibler–Distanz zwischen den Zufallsgrößen $X$ und $Y$:
- $$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} P_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)} \ge 0$$
- $$\Rightarrow \hspace{0.3cm}D(f_X \hspace{0.05cm} || \hspace{0.05cm}f_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{f_X(X)}{f_Y(X)}\right ] \hspace{0.2cm}= \hspace{-0.4cm}\int\limits_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{f_X(x)}{f_Y(x)} \hspace{0.15cm}{\rm d}x \ge 0 \hspace{0.05cm}.$$
Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen
Die Tabelle zeigt die Ergebnisse hinsichtlich der differentiellen Entropie für drei beispielhafte Wahrscheinlichkeitsdichtefunktionen $f_X(x)$. Diese sind alle spitzenwertbegrenzt, das heißt, es gilt jeweils $|X| ≤ A$.
- Bei »Spitzenwertbegrenzung« kann man die differentielle Entropie stets wie folgt darstellen:
- $$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$
- Anzufügen ist bei Verwendung von $\ln$ die Pseudo–Einheit „nat” und bei Verwendung von $\log_2$ die Pseudo–Einheit „bit”.
- Die Konstante ${\it \Gamma}_{\rm A}$ hängt allein von der WDF-Form ab und gilt nur für »Spitzenwertbegrenzung« ⇒ »$\rm A$mplitudenbegrenzung«.
- Eine Gleichverteilung im Bereich $|X| ≤ 1$ liefert $h(X) = 1$ bit, eine zweite im Bereich $|Y| ≤ 4$ dagegen zu $h(Y) = 3$ bit.
$\text{Theorem:}$ Unter der Nebenbedingung Spitzenwertbegrenzung (englisch: "Peak Constraint") ⇒ also WDF $f_X(x) = 0$ für $ \vert x \vert > A$ – führt die Gleichverteilung zur maximalen differentiellen Entropie:
- $$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$
Hier ist die geeignete Kenngröße ${\it \Gamma}_{\rm A} = 2$ maximal. Sie finden den Beweis am Ende dieses Kapitels.
Das Theorem bedeutet gleichzeitig, dass bei jeder anderen spitzenwertbegrenzten WDF (außer der Gleichverteilung) der Kennparameter ${\it \Gamma}_{\rm A} < 2$ ist.
- Für die symmetrische Dreieckverteilung ergibt sich nach obiger Tabelle ${\it \Gamma}_{\rm A} = \sqrt{\rm e} ≈ 1.649$.
- Beim einseitigen Dreieck $($zwischen $0$ und $A)$ ist demgegenüber ${\it \Gamma}_{\rm A}$ nur halb so groß.
- Auch für jedes andere Dreieck $($absolute Breite $A$, Spitze beliebig zwischen $0$ und $A)$ gilt ${\it \Gamma}_{\rm A} ≈ 0.824$.
Die jeweils zweite $h(X)$–Angabe und die Kenngröße ${\it \Gamma}_{\rm L}$ eignet sich dagegen für den Vergleich von Zufallsgrößen bei Leistungsbegrenzung, der im nächsten Abschnitt behandelt wird. Unter dieser Nebenbedingung ist zum Beispiel die symmetrische Dreieckverteilung $({\it \Gamma}_{\rm L} ≈ 16.31)$ besser als die Gleichverteilung ${\it \Gamma}_{\rm L} = 12)$.
Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen
In der folgenden Tabelle sind die differentiellen Entropien $h(X)$ für drei beispielhafte Dichtefunktionen $f_X(x)$ ohne Begrenzung zu entnehmen, die durch entsprechende Parameterwahl alle die gleiche Varianz $σ^2 = {\rm E}\big[|X -m_x|^2 \big]$ aufweisen. Berücksichtigt sind:
- die Gaußverteilung,
- die Laplaceverteilung ⇒ eine zweiseitige Exponentialverteilung,
- die (einseitige) Exponentialverteilung.
Bei »Leistungsbegrenzung« lässt sich die differentielle Entropie stets wie folgt darstellen:
- $$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2).$$
Das Ergebnis unterscheidet sich nur durch die Pseudo–Einheit
- „nat” bei Verwendung von $\ln$ bzw.
- „bit” bei Verwendung vo n $\log_2$.
$\text{Theorem:}$ Unter der Nebenbedingung der Leistungsbegrenzung (englisch: "Power Constraint") führt die Gaußverteilung,
- $$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm e}^{ - \hspace{0.05cm}{(x - m_1)^2}/(2 \sigma^2)},$$
unabhängig vom Mittelwert $m_1$ zur maximalen differentiellen Entropie:
- $$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$
Sie finden den Beweis am Ende dieses Kapitels.
Diese Aussage bedeutet gleichzeitig, dass für jede andere WDF als die Gaußverteilung die Kenngröße ${\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08$ sein wird.
Beispielsweise ergibt sich der Kennwert
- für die Dreieckverteilung zu ${\it \Gamma}_{\rm L} = 6{\rm e} ≈ 16.31$,
- für die Laplaceverteilung zu ${\it \Gamma}_{\rm L} = 2{\rm e}^2 ≈ 14.78$, und
- für die Gleichverteilung zu ${\it \Gamma}_{\rm L} = 12$ .
Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung
Unter der Nebenbedingung der »Spitzenwertbegrenzung« ⇒ $|X| ≤ A$ gilt für die differentielle Entropie:
- $$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Von allen möglichen Wahrscheinlichkeitsdichtefunktionen $f_X(x)$, die die Bedingung
- $$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$
erfüllen, ist nun diejenige Funktion $g_X(x)$ gesucht, die zur maximalen differentiellen Entropie $h(X)$ führt.
Zur Herleitung benutzen wir das Verfahren der Lagrange–Multiplikatoren:
- Wir definieren die Lagrange–Kenngröße $L$ in der Weise, dass darin sowohl $h(X)$ als auch die Nebenbedingung $|X| ≤ A$ enthalten sind:
- $$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
- Wir setzen allgemein $f_X(x) = g_X(x) + ε · ε_X(x)$, wobei $ε_X(x)$ eine beliebige Funktion darstellt, mit der Einschränkung, dass die WDF–Fläche gleich $1$ sein muss. Damit erhalten wir:
- $$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm}\big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x)\big ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$
- Die bestmögliche Funktion ergibt sich dann, wenn es für $ε = 0$ eine stationäre Lösung gibt:
- $$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 \hspace{0.05cm}.$$
- Diese Bedingungsgleichung ist unabhängig von $ε_X$ nur dann zu erfüllen, wenn gilt:
- $${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} \forall x \in \big[-A, +A \big]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} g_X(x) = {\rm const.}\hspace{0.4cm} \forall x \in \big [-A, +A \big]\hspace{0.05cm}.$$
$\text{Resümee bei Spitzenwertbegrenzung:}$
Die maximale differentielle Entropie ergibt sich unter der Nebenbedingung $ \vert X \vert ≤ A$ für die Gleichverteilung (englisch: "Uniform PDF"):
- $$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 \hspace{0.05cm}.$$
Jede andere Zufallsgröße mit der WDF–Eigenschaft $f_X(\vert x \vert > A) = 0$ führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch den Parameter ${\it \Gamma}_{\rm A} < 2$.
Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung
Vorneweg zur Begriffserklärung:
- Eigentlich wird nicht die Leistung ⇒ das zweite Moment $m_2$ begrenzt, sondern das zweite Zentralmoment ⇒ Varianz $μ_2 = σ^2$.
- Gesucht wird also nun die maximale differentielle Entropie unter der Nebenbedingung ${\rm E}\big[|X – m_1|^2 \big] ≤ σ^2$.
- Das $≤$–Zeichen dürfen wir hierbei durch das Gleichheitszeichen ersetzen.
Lassen wir nur mittelwertfreie Zufallsgrößen zu, so umgehen wir das Problem. Damit lautet der Lagrange-Multiplikator:
- $$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_1 \cdot \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_2 \cdot \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Nach ähnlichem Vorgehen wie beim Beweis für Spitzenwertbegrenzung zeigt sich, dass die „bestmögliche” Funktion $g_X(x) \sim {\rm e}^{–λ_2\hspace{0.05cm} · \hspace{0.05cm} x^2}$ sein muss ⇒ Gaußverteilung:
- $$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$
Wir verwenden hier aber für den expliziten Beweis die Kullback–Leibler–Distanz zwischen einer geeigneten allgemeinen WDF $f_X(x)$ und der Gauß–WDF $g_X(x)$:
- $$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \frac{f_X(x)}{g_X(x)} \hspace{0.1cm}{\rm d}x = -h(X) - I_2\hspace{0.3cm} \Rightarrow\hspace{0.3cm}I_2 = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Zur Vereinfachung ist hier der natürliche Logarithmus ⇒ $\ln$ verwendet. Damit erhalten wir für das zweite Integral:
- $$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.3cm}- \hspace{0.3cm} \frac{1}{2\sigma^2} \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{0.02cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Das erste Integral ist definitionsgemäß gleich $1$ und das zweite Integral ergibt $σ^2$:
- $$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$
- $$\Rightarrow\hspace{0.3cm} D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = -h(X) - I_2 = -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
Da auch bei wertkontinuierlichen Zufallsgrößen die Kullback–Leibler–Distanz stets $\ge 0$ ist, erhält man nach Verallgemeinerung („ln” ⇒ „log”):
- $$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
Das Gleichzeichen gilt nur, wenn die Zufallsgröße $X$ gaußverteilt ist.
$\text{Resümee bei Leistungsbegrenzung:}$
Die maximale differentielle Entropie ergibt sich unter der Bedingung ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ unabhängig von $m_1$ für die Gaußverteilung (englisch: "Gaussian PDF"):
- $$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} \hspace{0.05cm}.$$
Jede andere wertkontinuierliche Zufallsgröße $X$ mit Varianz ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ führt zu einem kleineren Wert, gekennzeichnet durch die Kenngröße ${\it \Gamma}_{\rm L} < 2πe$.
Aufgaben zum Kapitel
Aufgabe 4.1: WDF, VTF und Wahrscheinlichkeit
Aufgabe 4.1Z: Momentenberechnung
Aufgabe 4.2: Dreieckförmige WDF
Aufgabe 4.2Z: Gemischte Zufallsgrößen
Aufgabe 4.3: WDF–Vergleich bezüglich differentieller Entropie
Aufgabe 4.3Z: Exponential– und Laplaceverteilung
Aufgabe 4.4: Herkömmliche Entropie und differenzielle Entropie