Informationstheorie/Verschiedene Entropien zweidimensionaler Zufallsgrößen: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (37 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
| − | ==Definition der Entropie unter Verwendung von supp(<i>P<sub>XY</sub></i>)== | + | ==Definition der Entropie unter Verwendung von supp(<i>P<sub>XY</sub></i>)== |
| − | Wir fassen die Ergebnisse des letzten | + | <br> |
| + | Wir fassen die Ergebnisse des letzten Kapitels nochmals kurz zusammen, wobei wir von der zweidimensionalen Zufallsgröße $XY$ mit der Wahrscheinlichkeitsfunktion $P_{XY}(X,\ Y)$ ausgehen. Gleichzeitig verwenden wir die Schreibweise | ||
| − | Mit dieser Teilmenge $\text{supp}(P_{XY}) ⊂ P_{XY}$ gilt für | + | :$${\rm supp} (P_{XY}) = \big \{ \hspace{0.05cm}(x,\ y) \in XY \hspace{0.05cm}, |
| − | *die '''Verbundentropie''' (englisch: | + | \hspace{0.3cm} {\rm wobei} \hspace{0.15cm} P_{XY}(X,\ Y) \ne 0 \hspace{0.05cm} \big \} \hspace{0.05cm}.$$ |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Zusammenfassende Darstellung des letzten Kapitels:}$ Mit dieser Teilmenge $\text{supp}(P_{XY}) ⊂ P_{XY}$ gilt für | ||
| + | *die '''Verbundentropie''' (englisch: "Joint Entropy"): | ||
| − | *die '''Entropien der 1D–Zufallsgrößen''' $X$ und $Y$: | + | :$$H(XY) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.05cm})} |
| + | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(x, y)} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *die '''Entropien der 1D–Zufallsgrößen''' $X$ und $Y$: | ||
| + | :$$H(X) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ] =\hspace{-0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{X})} | ||
| + | \hspace{-0.2cm} P_{X}(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(x)} \hspace{0.05cm},$$ | ||
| + | :$$H(Y) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(Y)}\right ] =\hspace{-0.2cm} \sum_{y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Y})} | ||
| + | \hspace{-0.2cm} P_{Y}(y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(y)} \hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Wir beziehen uns nochmals auf die Beispiele auf der Seite [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|Verbundwahrscheinlichkeit und Verbundentropie]] im letzten Kapitel. | ||
| − | {{Beispiel}} | + | Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RB}(R, B)$ im dortigen [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|$\text{Beispiel 5}$]] mit den Parametern |
| − | Bei der | + | *$R$ ⇒ Augenzahl des roten Würfels und |
| − | * $R$ | + | *$B$ ⇒ Augenzahl des blauen Würfels |
| − | * $S$ | + | |
| − | gibt es 6 · 11 = 66 Felder, von denen viele leer sind | + | |
| − | Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da $x · \log_2 ( | + | sind die Mengen $P_{RB}$ und $\text{supp}(P_{RB})$ identisch. Hier sind alle $6^2 = 36$ Felder mit Werten ungleich Null belegt. |
| − | + | ||
| − | + | Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RS}(R, S)$ im [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|$\text{Beispiel 6}$]] mit den Parametern | |
| − | + | *$R$ ⇒ Augenzahl des roten Würfels und | |
| − | + | *$S = R + B$ ⇒ Summe der beiden Würfel | |
| − | + | ||
| − | + | ||
| + | gibt es $6 · 11 = 66$ Felder, von denen allerdings viele leer sind, also für die Wahrscheinlichkeit „0” stehen. | ||
| + | *Die Teilmenge $\text{supp}(P_{RS})$ beinhaltet dagegen nur die $36$ schraffierten Felder mit von Null verschiedenen Wahrscheinlichkeiten. | ||
| + | *Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da für $x → 0$ der Grenzwert $x · \log_2 ({1}/{x}) = 0$ ist.}} | ||
==Bedingte Wahrscheinlichkeit und bedingte Entropie == | ==Bedingte Wahrscheinlichkeit und bedingte Entropie == | ||
| + | <br> | ||
| + | Im Buch „Stochastische Signaltheorie” wurden für den Fall zweier Ereignisse $X$ und $Y$ die folgenden [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit|bedingten Wahrscheinlichkeiten]] angegeben ⇒ '''Satz von Bayes''': | ||
| + | |||
| + | :$${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} | ||
| + | {\rm Pr} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (X)} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
Angewendet auf Wahrscheinlichkeitsfunktionen erhält man somit: | Angewendet auf Wahrscheinlichkeitsfunktionen erhält man somit: | ||
| − | + | :$$P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{P_{XY}(X, Y)}{P_{Y}(Y)} \hspace{0.05cm}, \hspace{0.5cm} | |
| + | P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{P_{XY}(X, Y)}{P_{X}(X)} \hspace{0.05cm}.$$ | ||
| + | Analog zur [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Definition_der_Entropie_unter_Verwendung_von_supp.28PXY.29|Verbundentropie]] $H(XY)$ lassen sich hier folgende Entropiefunktionen ableiten: | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | Die '''bedingte Entropie''' (englisch: | + | $\text{Definitionen:}$ |
| + | *Die '''bedingte Entropie''' (englisch: "Conditional Entropy") der Zufallsgröße $X$ unter der Bedingung $Y$ lautet: | ||
| − | In gleicher Weise erhält man für die zweite bedingte Entropie: | + | :$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} |
| + | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | ||
| + | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{Y}(y)}{P_{XY}(x, y)} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *In gleicher Weise erhält man für die '''zweite bedingte Entropie''': | ||
| + | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | ||
| + | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | ||
| + | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} | ||
| + | \hspace{0.05cm}.$$}} | ||
| − | |||
| + | Im Argument der Logarithmusfunktion steht stets eine bedingte Wahrscheinlichkeitsfunktion ⇒ $P_{X\hspace{0.03cm}| \hspace{0.03cm}Y}(·)$ bzw. $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(·)$, während zur Erwartungswertbildung die Verbundwahrscheinlichkeit ⇒ $P_{XY}(·)$ benötigt wird. | ||
| − | |||
Für die bedingten Entropien gibt es folgende Begrenzungen: | Für die bedingten Entropien gibt es folgende Begrenzungen: | ||
| − | *Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich | + | *Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich Null. Aus $H(X|Y) = 0$ folgt direkt auch $H(Y|X) = 0$. Beides ist nur für [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Disjunkte_Mengen|disjunkte Mengen]] $X$ und $Y$ möglich. |
| − | *Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese | + | *Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese Aussagen sind einleuchtend, wenn man sich bewusst macht, dass man für „Entropie” synonym auch „Unsicherheit” verwenden kann. Denn: Die Unsicherheit bezüglich der Menge $X$ kann nicht dadurch größer werden, dass man $Y$ kennt. |
| − | + | *Außer bei statistischer Unabhängigkeit ⇒ $H(X|Y) = H(X)$ gilt stets $H(X|Y) < H(X)$. Wegen $H(X) ≤ H(XY)$ und $H(Y) ≤ H(XY)$ gilt somit auch $H(X|Y) ≤ H(XY)$ und $H(Y|X) ≤ H(XY)$. Eine bedingte Entropie kann also nie größer werden als die Verbundentropie. | |
| − | |||
| − | {{Beispiel}} | + | {{GraueBox|TEXT= |
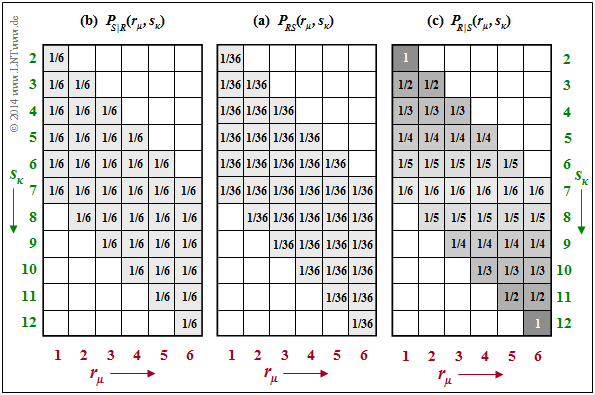
| + | $\text{Beispiel 2:}$ Wir betrachten die Verbundwahrscheinlichkeiten $P_{RS}(·)$ unseres Würfelexperiments, die im [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|letzten Kapitel]] als $\text{Beispiel 6}$ ermittelt wurden. In der Mitte der folgenden Grafik ist die damals berechnete Verbundwahrscheinlichkeit $P_{RS}(·)$ nochmals angegeben. | ||
| − | + | [[Datei:P_ID2764__Inf_T_3_2_S3.png|right|frame|Verbundwahrscheinlichkeiten $P_{RS}$ und bedingte Wahrscheinlichkeiten $P_{S \vert R}$ und $P_{R \vert S}$]] | |
| − | Außen sind die beiden bedingten Wahrscheinlichkeitsfunktionen | + | Außen sind die beiden bedingten Wahrscheinlichkeitsfunktionen dargestellt: |
| − | + | ||
| + | $\rm Links$ angegeben ist die bedingte Wahrscheinlichkeitsfunktion | ||
| + | :$$P_{S \vert R}(⋅) = P_{SR}(⋅)/P_R(⋅).$$ | ||
| + | *Wegen $P_R(R) = \big [1/6, \ 1/6, \ 1/6, \ 1/6, \ 1/6, \ 1/6 \big ]$ steht hier in allen schraffierten Feldern ⇒ $\text{supp}(P_{S\vert R}) = \text{supp}(P_{R\vert S})$ der gleiche Wahrscheinlichkeitswert $1/6$. | ||
| + | *Daraus folgt für die bedingte Entropie: | ||
| − | + | :$$H(S \hspace{-0.1cm}\mid \hspace{-0.13cm} R) = \hspace{-0.2cm} \sum_{(r, s) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{RS})} | |
| + | \hspace{-0.6cm} P_{RS}(r, s) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}S \hspace{0.03cm} \mid \hspace{0.03cm} R} (s \hspace{-0.05cm}\mid \hspace{-0.05cm} r)} $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}H(S \hspace{-0.1cm}\mid \hspace{-0.13cm} R) = | ||
| + | 36 \cdot \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | $\rm Rechts$ ist $P_{R\vert S}(⋅) = P_{RS}(⋅)/P_S(⋅)$ angegeben, wobei $P_S(⋅)$ gemäß [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|$\text{Beispiel 6}$]] einzusetzen ist. | ||
| + | *Es ergeben sich die gleichen Felder ungleich Null ⇒ $\text{supp}(P_{R\vert S}) = \text{supp}(P_{S\vert R})$. | ||
| + | * Die Wahrscheinlichkeitswerte nehmen nun aber von der Mitte $(1/6)$ zu den Rändern hin bis zur Wahrscheinlichkeit $1$ in den Ecken kontinuierlich zu. Daraus folgt: | ||
| − | + | :$$H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} S) = \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) + | |
| + | \frac{2}{36} \cdot \sum_{i=1}^5 \big [ i \cdot {\rm log}_2 \hspace{0.1cm} (i) \big ]= 1.896\ {\rm bit} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Für die bedingten Wahrscheinlichkeiten der 2D–Zufallsgröße $RB$ gemäß [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|$\text{Beispiel 5}$]] erhält man dagegen wegen $P_{RB}(⋅) = P_R(⋅) · P_B(⋅)$: | ||
| + | :$$\begin{align*}H(B \hspace{-0.1cm}\mid \hspace{-0.13cm} R) \hspace{-0.15cm} & = \hspace{-0.15cm} H(B) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm},\\ | ||
| + | H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} B) \hspace{-0.15cm} & = \hspace{-0.15cm} H(R) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm}.\end{align*}$$}} | ||
| − | |||
| − | ==Transinformation zwischen zwei Zufallsgrößen | + | ==Transinformation zwischen zwei Zufallsgrößen== |
| + | <br> | ||
| + | Wir betrachten die Zufallsgröße $XY$ mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$. Bekannt seien auch die 1D–Funktionen $P_X(X)$ und $P_Y(Y)$. | ||
| + | |||
| + | Nun stellen sich folgende Fragen: | ||
| + | *Wie vermindert die Kenntnis der Zufallsgröße $Y$ die Unsicherheit bezüglich $X$? | ||
| + | *Wie vermindert die Kenntnis der Zufallsgröße $X$ die Unsicherheit bezüglich $Y$? | ||
| + | |||
| − | |||
| − | |||
| − | |||
Zur Beantwortung benötigen wir eine für die Informationstheorie substantielle Definition: | Zur Beantwortung benötigen wir eine für die Informationstheorie substantielle Definition: | ||
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | Die '''Transinformation''' (englisch: | + | $\text{Definition:}$ Die '''Transinformation''' (englisch: "Mutual Information") zwischen den Zufallsgrößen $X$ und $Y$ – beide über dem gleichen Alphabet – ist wie folgt gegeben: |
| − | Ein Vergleich mit Kapitel | + | :$$I(X;\ Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} |
| + | {P_{X}(X) \cdot P_{Y}(Y) }\right ] =\hspace{-0.25cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY})} | ||
| + | \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(x, y)} | ||
| + | {P_{X}(x) \cdot P_{Y}(y) } \hspace{0.01cm}.$$ | ||
| + | |||
| + | Ein Vergleich mit dem [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Einf.C3.BChrungsbeispiel_zur_statistischen_Abh.C3.A4ngigkeit_von_Zufallsgr.C3.B6.C3.9Fen|letzten Kapitel]] zeigt, dass die Transinformation auch als [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Relative_Entropie_.E2.80.93_Kullback.E2.80.93Leibler.E2.80.93Distanz|Kullback–Leibler–Distanz]] zwischen der 2D–PMF $P_{XY}$ und dem Produkt $P_X · P_Y$ geschrieben werden kann: | ||
| − | + | :$$I(X;Y) = D(P_{XY} \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_X \cdot P_Y) \hspace{0.05cm}.$$ | |
| − | + | Es ist somit offensichtlich, dass stets $I(X;\ Y) ≥ 0$ gilt. Wegen der Symmetrie ist auch $I(Y;\ X)$ = $I(X;\ Y)$.}} | |
| − | Sucht man in einem Wörterbuch die Übersetzung für „mutual”, so findet man unter Anderem die Begriffe „gemeinsam”, „gegenseitig”, „beidseitig” und „wechselseitig”. Und ebenso sind in Fachbüchern für $I(X; Y)$ auch die Bezeichnungen | + | Sucht man in einem Wörterbuch die Übersetzung für „mutual”, so findet man unter Anderem die Begriffe „gemeinsam”, „gegenseitig”, „beidseitig” und „wechselseitig”. Und ebenso sind in Fachbüchern für $I(X; Y)$ auch die Bezeichnungen „gemeinsame Entropie” und „'gegenseitige Entropie” üblich. Wir sprechen aber im Folgenden durchgängig von der „Transinformation” $I(X; Y)$ und versuchen nun eine Interpretation dieser Größe: |
| − | *Durch Aufspalten des | + | *Durch Aufspalten des $\log_2$–Arguments entsprechend |
| − | erhält man unter Verwendung von $P_{X|Y}( | + | :$$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac{1} |
| + | {P_{X}(X) }\right ] - {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac | ||
| + | {P_{Y}(Y) }{P_{XY}(X, Y)} \right ] $$ | ||
| + | |||
| + | :erhält man unter Verwendung von $P_{X|Y}(\cdot) = P_{XY}(\cdot)/P_Y(Y)$: | ||
| − | Das heißt: Die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ vermindert sich bei Kenntnis von $Y$ um den Betrag $H(X|Y)$. Der Rest ist die Transinformation $I(X; Y)$. | + | :$$I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) \hspace{0.05cm}.$$ |
| − | *Bei anderer Aufspaltung kommt man zum Ergebnis: | + | |
| + | *Das heißt: Die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ vermindert sich bei Kenntnis von $Y$ um den Betrag $H(X|Y)$. Der Rest ist die Transinformation $I(X; Y)$. | ||
| + | *Bei anderer Aufspaltung kommt man zum Ergebnis | ||
| + | :$$I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$ | ||
| + | *Ergo: Die Transinformation $I(X; Y)$ ist symmetrisch ⇒ $X$ sagt genau so viel über $Y$ aus wie $Y$ über $X$ ⇒ gegenseitige Information. Das Semikolon weist auf die Gleichberechtigung hin. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ | ||
| + | Oft werden die hier genannten Gleichungen durch ein Schaubild verdeutlicht, so auch in den folgenden Beispielen. Daraus erkennt man, dass auch folgende Gleichungen zutreffen: | ||
| − | + | :$$I(X;\ Y) = H(X) + H(Y) - H(XY) \hspace{0.05cm},$$ | |
| + | :$$I(X;\ Y) = H(XY) - | ||
| + | H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) | ||
| + | \hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
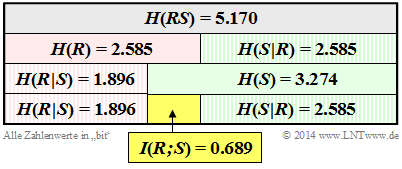
| + | $\text{Beispiel 3:}$ Wir kommen (letztmalig) auf das [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Einf.C3.BChrungsbeispiel_zur_statistischen_Abh.C3.A4ngigkeit_von_Zufallsgr.C3.B6.C3.9Fen|Würfel–Experiment]] mit dem roten $(R)$ und dem blauen $(B)$ Würfel zurück. Die Zufallsgröße $S$ gibt die Summe der beiden Würfel an: $S = R + B$. | ||
| + | Wir betrachten hier die 2D–Zufallsgröße $RS$. In früheren Beispielen haben wir berechnet: | ||
| + | *die Entropien $H(R) = 2.585 \ \rm bit$ und $H(S) = 3.274 \ \rm bit$ ⇒ [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|Beispiel 6]] im letzten Kapitel, | ||
| + | *die Verbundentropie $H(RS) = 5.170 \ \rm bit$ ⇒ [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|Beispiel 6]] im letzten Kapitel, | ||
| + | *die bedingten Entropien $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R) = 2.585 \ \rm bit$ und $H(R \hspace{0.05cm} \vert \hspace{0.05cm} S) = 1.896 \ \rm bit$ ⇒ [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Bedingte_Wahrscheinlichkeit_und_bedingte_Entropie|Beispiel 2]] im vorherigen Abschnitt. | ||
| + | |||
| − | + | [[Datei:P_ID2765__Inf_T_3_2_S3_neu.png|frame|Schaubild aller Entropien des „Würfelexperiments” ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Diese Größen sind in der Grafik zusammengestellt, wobei die Zufallsgröße $R$ durch die Grundfarbe „Rot” und die Summe $S$ durch die Grundfarbe | + | Diese Größen sind in der Grafik zusammengestellt, wobei die Zufallsgröße $R$ durch die Grundfarbe „Rot” und die Summe $S$ durch die Grundfarbe „Grün” markiert sind. Bedingte Entropien sind schraffiert. |
Man erkennt aus dieser Darstellung: | Man erkennt aus dieser Darstellung: | ||
| − | * | + | *Die Entropie $H(R) = \log_2 (6) = 2.585\ \rm bit$ ist genau halb so groß wie die Verbundentropie $H(RS)$. Denn: Kennt man $R$, so liefert $S$ genau die gleiche Information wie die Zufallsgröße $B$, nämlich $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R) = H(B) = \log_2 (6) = 2.585\ \rm bit$. |
| − | *Die Entropie $H(S) | + | *'''Hinweis''': $H(R)$ = $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ '''gilt allerdings nicht allgemein''', sondern nur in diesem Beispiel. |
| − | *Die Transinformation (englisch: ''Mutual Information'') zwischen den Zufallsgrößen $R$ und $S$ ergibt sich aber auch aus der Gleichung | + | *Die Entropie $H(S) = 3.274 \ \rm bit$ ist im vorliegenden Beispiel erwartungsgemäß größer als $H(R)= 2.585\ \rm bit$. Wegen $H(S) + H(R \hspace{0.05cm} \vert \hspace{0.05cm} S) = H(R) + H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ muss deshalb $H(R \hspace{0.05cm} \vert \hspace{0.05cm} S)$ gegenüber $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ um den gleichen Betrag $I(R;\ S) = 0.689 \ \rm bit$ kleiner sein als $H(R)$ gegenüber $H(S)$. |
| − | + | *Die Transinformation (englisch: '''Mutual Information''') zwischen den Zufallsgrößen $R$ und $S$ ergibt sich aber auch aus der Gleichung | |
| − | + | :$$I(R;\ S) = H(R) + H(S) - H(RS) = 2.585\ {\rm bit} + 3.274\ {\rm bit} - 5.170\ {\rm bit} = 0.689\ {\rm bit} \hspace{0.05cm}. $$}} | |
| − | {{ | ||
==Bedingte Transinformation == | ==Bedingte Transinformation == | ||
| + | <br> | ||
| + | Wir betrachten nun drei Zufallsgrößen $X$, $Y$ und $Z$, die zueinander in Beziehung stehen (können). | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Die '''bedingte Transinformation''' (englisch: "Conditional Mutual Information") zwischen den Zufallsgrößen $X$ und $Y$ '''bei gegebenem''' $Z = z$ lautet: | ||
| + | |||
| + | :$$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z = z) - H(X\vert\hspace{0.05cm}Y ,\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$ | ||
| − | + | Man bezeichnet als die '''bedingte Transinformation''' zwischen den Zufallsgrößen $X$ und $Y$ für die Zufallsgröße $Z$ '''allgemein''' nach Mittelung über alle $z \in Z$: | |
| − | |||
| − | + | :$$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z ) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z ) - H(X\vert\hspace{0.05cm}Y Z )= \hspace{-0.3cm} | |
| − | + | \sum_{z \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Z})} \hspace{-0.25cm} P_{Z}(z) \cdot | |
| − | + | I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) | |
| + | \hspace{0.05cm}.$$ | ||
| − | + | $P_Z(Z)$ ist die Wahrscheinlichkeitsfunktion $\rm (PMF)$ der Zufallsgröße $Z$ und $P_Z(z)$ die Wahrscheinlichkeit für die Realisierung $Z = z$.}} | |
| − | Bitte beachten Sie: Für die bedingte Entropie gilt bekanntlich die Größenrelation $H(X | + | {{BlaueBox|TEXT= |
| − | + | $\text{Bitte beachten Sie:}$ | |
| + | *Für die bedingte Entropie gilt bekanntlich die Größenrelation $H(X\hspace{0.05cm}\vert\hspace{0.05cm}Z) ≤ H(X)$. | ||
| + | *Für die Transinformation gilt diese Größenrelation nicht unbedingt: | ||
| + | *$I(X; Y\hspace{0.05cm}\vert\hspace{0.05cm}Z)$ kann '''kleiner, gleich, aber auch größer sein''' als $I(X; Y)$.}} | ||
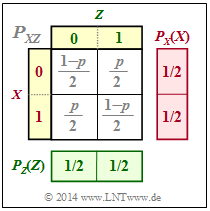
| − | {{Beispiel} | + | [[Datei:P_ID2824__Inf_T_3_2_S4a.png|right|frame|2D–PMF $P_{XZ}$ ]] |
| − | Wir betrachten die binären Zufallsgrößen $X$, $Y$ und $Z$ mit folgenden Eigenschaften: | + | {{GraueBox|TEXT= |
| − | * $X$ und $Y$ seien statistisch unabhängig | + | $\text{Beispiel 4:}$ |
| + | Wir betrachten die binären Zufallsgrößen $X$, $Y$ und $Z$ mit folgenden Eigenschaften: | ||
| + | * $X$ und $Y$ seien statistisch unabhängig. Für ihre Wahrscheinlichkeitsfunktionen gelte: | ||
| + | :$$P_X(X) = \big [1/2, \ 1/2 \big], \hspace{0.2cm} P_Y(Y) = \big[1– p, \ p \big] \ ⇒ \ H(X) = 1\ {\rm bit}, \hspace{0.2cm} H(Y) = H_{\rm bin}(p).$$ | ||
| + | * $Z$ ist die Modulo–2–Summe von $X$ und $Y$: $Z = X ⊕ Y$. | ||
| − | |||
| − | Aus der | + | Aus der Verbund–Wahrscheinlichkeitsfunktion $P_{XZ}$ gemäß der oberen Grafik folgt: |
| − | *Durch Summation der Spalten–Wahrscheinlichkeiten ergibt sich $P_Z(Z) | + | *Durch Summation der Spalten–Wahrscheinlichkeiten ergibt sich $P_Z(Z) = \big [1/2, \ 1/2 \big ]$ ⇒ $H(Z) = 1\ {\rm bit}$. |
| − | * $X$ und $Z$ sind ebenfalls statistisch unabhängig, da für die 2D–PMF $P_{XZ}(X, Z) | + | * $X$ und $Z$ sind ebenfalls statistisch unabhängig, da für die 2D–PMF $P_{XZ}(X, Z) = P_X(X) · P_Z(Z)$ gilt. |
| − | *Daraus folgt: $H(Z | + | *Daraus folgt: $H(Z\hspace{0.05cm}\vert\hspace{0.05cm} X) = H(Z)$ und $H(X \hspace{0.05cm}\vert\hspace{0.05cm} Z) = H(X)$ sowie $I(X; Z) = 0$. |
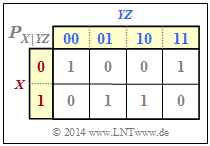
| + | [[Datei:P_ID2826__Inf_T_3_2_S4b.png|right|frame|Bedingte 2D–PMF $P_{X\hspace{0.05cm}\vert\hspace{0.05cm}YZ}$]] | ||
| + | <br><br>Aus der bedingten Wahrscheinlichkeitsfunktion $P_{X\vert YZ}$ gemäß der unteren Grafik lassen sich berechnen: | ||
| + | * $H(X\hspace{0.05cm}\vert\hspace{0.05cm} YZ) = 0$, da alle $P_{X\hspace{0.05cm}\vert\hspace{0.05cm} YZ}$–Einträge entweder $0$ oder $1$ sind ⇒ „bedingte Entropie”, | ||
| + | * $I(X; YZ) = H(X) - H(X\hspace{0.05cm}\vert\hspace{0.05cm} YZ) = H(X)= 1 \ {\rm bit}$ ⇒ „Transinformation”, | ||
| + | * $I(X; Y\vert Z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z) =H(X)=1 \ {\rm bit} $ ⇒ „bedingte Transinformation”. | ||
| − | |||
| − | + | '''Im vorliegenden Beispiel ist''' also | |
| − | + | *'''die bedingte Transinformation''' $I(X; Y\hspace{0.05cm}\vert\hspace{0.05cm} Z) = 1$ | |
| − | * | + | *'''größer als die herkömmliche Transinformation''' $I(X; Y) = 0$. }} |
| − | |||
| − | |||
| − | |||
| − | |||
==Kettenregel der Transinformation == | ==Kettenregel der Transinformation == | ||
| + | <br> | ||
| + | Bisher haben wir die Transinformation nur zwischen zwei eindimensionalen Zufallsgrößen betrachtet. Nun erweitern wir die Definition auf insgesamt $n + 1$ Zufallsgrößen, die wir aus Darstellungsgründen mit $X_1$, ... , $X_n$ sowie $Z$ bezeichnen. Dann gilt: | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Kettenregel der Transinformation:}$ | ||
| + | |||
| + | Die Transinformation zwischen der $n$–dimensionalen Zufallsgröße $X_1 X_2 \hspace{0.05cm}\text{...} \hspace{0.05cm} X_n$ und der Zufallsgröße $Z$ lässt sich wie folgt darstellen und berechnen: | ||
| + | |||
| + | :$$I(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n;Z) = | ||
| + | I(X_1;Z) + I(X_2;Z \vert X_1) + \hspace{0.05cm}\text{...} \hspace{0.1cm}+ | ||
| + | I(X_n;Z\vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{n-1}) = \sum_{i = 1}^{n} | ||
| + | I(X_i;Z \vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) | ||
| + | \hspace{0.05cm}.$$}} | ||
| − | {{ | + | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Beweis:}$ | |
| + | Wir beschränken uns hier auf den Fall $n = 2$, also auf insgesamt drei Zufallsgrößen, und ersetzen $X_1$ durch $X$ und $X_2$ durch $Y$. Dann erhalten wir: | ||
| + | :$$\begin{align*}I(X\hspace{0.05cm}Y;Z) & = H(XY) - H(XY\hspace{0.05cm} \vert \hspace{0.05cm}Z) = \\ | ||
| + | & = \big [ H(X)+ H(Y\hspace{0.05cm} \vert \hspace{0.05cm} X)\big ] - \big [ H(X\hspace{0.05cm} \vert \hspace{0.05cm} Z) + H(Y\hspace{0.05cm} \vert \hspace{0.05cm} XZ)\big ] =\\ | ||
| + | & = \big [ H(X)- H(X\hspace{0.05cm} \vert \hspace{0.05cm} Z)\big ] - \big [ H(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) + H(Y\hspace{0.05cm} \vert \hspace{0.05cm}XZ)\big ]=\\ | ||
| + | & = I(X;Z) + I(Y;Z \hspace{0.05cm} \vert \hspace{0.05cm} X) \hspace{0.05cm}.\end{align*}$$}} | ||
| − | |||
| + | Aus dieser Gleichung erkennt man, dass die die Größenrelation $I(X Y; Z) ≥ I(X; Z)$ immer gegeben ist. | ||
| + | *Gleichheit ergibt sich für die bedingte Transinformation $I(Y; Z \hspace{0.05cm} \vert \hspace{0.05cm} X) = 0$, | ||
| + | * also dann, wenn die Zufallsgrößen $Y$ und $Z$ für ein gegebenes $X$ statistisch unabhängig sind. | ||
| − | + | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 5:}$ Wir betrachten die [[Stochastische_Signaltheorie/Markovketten|Markovkette]] $X → Y → Z$. Für eine solche Konstellation gilt stets das '''Data Processing Theorem''' mit der folgenden Konsequenz, die sich aus der Kettenregel der Transinformation ableiten lässt: | ||
| − | + | :$$I(X;Z) \hspace{-0.05cm} \le \hspace{-0.05cm}I(X;Y ) \hspace{0.05cm},$$ | |
| + | :$$I(X;Z) \hspace{-0.05cm} \le \hspace{-0.05cm} I(Y;Z ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Das Theorem besagt somit: | ||
| + | *Man kann durch Manipulation $($"Processing" $Z)$ der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen. | ||
| + | *Die Datenverarbeitung $Y → Z$ $($durch einen zweiten Prozessor$)$ dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen. | ||
| − | + | Weitere Informationen zum "Data Processing Theorem" finden Sie in der [[Aufgaben:Aufgabe_3.15:_Data_Processing_Theorem|Aufgabe 3.15]].}} | |
| − | + | ||
| − | + | ||
| − | + | ==Aufgaben zum Kapitel== | |
| − | + | <br> | |
| − | + | [[Aufgaben:3.7 Einige Entropieberechnungen|Aufgabe 3.7: Einige Entropieberechnungen]] | |
| − | + | [[Aufgaben:3.8 Nochmals Transinformation|Aufgabe 3.8: Nochmals Transinformation]] | |
| − | + | [[Aufgaben:3.8Z Tupel aus ternären Zufallsgrößen|Aufgabe 3.8Z: Tupel aus ternären Zufallsgrößen]] | |
| + | [[Aufgaben:3.9 Bedingte Transinformation|Aufgabe 3.9: Bedingte Transinformation]] | ||
| − | |||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 19. Juli 2021, 16:25 Uhr
Inhaltsverzeichnis
Definition der Entropie unter Verwendung von supp(PXY)
Wir fassen die Ergebnisse des letzten Kapitels nochmals kurz zusammen, wobei wir von der zweidimensionalen Zufallsgröße $XY$ mit der Wahrscheinlichkeitsfunktion $P_{XY}(X,\ Y)$ ausgehen. Gleichzeitig verwenden wir die Schreibweise
- $${\rm supp} (P_{XY}) = \big \{ \hspace{0.05cm}(x,\ y) \in XY \hspace{0.05cm}, \hspace{0.3cm} {\rm wobei} \hspace{0.15cm} P_{XY}(X,\ Y) \ne 0 \hspace{0.05cm} \big \} \hspace{0.05cm}.$$
$\text{Zusammenfassende Darstellung des letzten Kapitels:}$ Mit dieser Teilmenge $\text{supp}(P_{XY}) ⊂ P_{XY}$ gilt für
- die Verbundentropie (englisch: "Joint Entropy"):
- $$H(XY) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.05cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(x, y)} \hspace{0.05cm}.$$
- die Entropien der 1D–Zufallsgrößen $X$ und $Y$:
- $$H(X) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ] =\hspace{-0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{X})} \hspace{-0.2cm} P_{X}(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(x)} \hspace{0.05cm},$$
- $$H(Y) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(Y)}\right ] =\hspace{-0.2cm} \sum_{y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Y})} \hspace{-0.2cm} P_{Y}(y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(y)} \hspace{0.05cm}.$$
$\text{Beispiel 1:}$ Wir beziehen uns nochmals auf die Beispiele auf der Seite Verbundwahrscheinlichkeit und Verbundentropie im letzten Kapitel.
Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RB}(R, B)$ im dortigen $\text{Beispiel 5}$ mit den Parametern
- $R$ ⇒ Augenzahl des roten Würfels und
- $B$ ⇒ Augenzahl des blauen Würfels
sind die Mengen $P_{RB}$ und $\text{supp}(P_{RB})$ identisch. Hier sind alle $6^2 = 36$ Felder mit Werten ungleich Null belegt.
Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RS}(R, S)$ im $\text{Beispiel 6}$ mit den Parametern
- $R$ ⇒ Augenzahl des roten Würfels und
- $S = R + B$ ⇒ Summe der beiden Würfel
gibt es $6 · 11 = 66$ Felder, von denen allerdings viele leer sind, also für die Wahrscheinlichkeit „0” stehen.
- Die Teilmenge $\text{supp}(P_{RS})$ beinhaltet dagegen nur die $36$ schraffierten Felder mit von Null verschiedenen Wahrscheinlichkeiten.
- Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da für $x → 0$ der Grenzwert $x · \log_2 ({1}/{x}) = 0$ ist.
Bedingte Wahrscheinlichkeit und bedingte Entropie
Im Buch „Stochastische Signaltheorie” wurden für den Fall zweier Ereignisse $X$ und $Y$ die folgenden bedingten Wahrscheinlichkeiten angegeben ⇒ Satz von Bayes:
- $${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} {\rm Pr} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (X)} \hspace{0.05cm}.$$
Angewendet auf Wahrscheinlichkeitsfunktionen erhält man somit:
- $$P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{P_{XY}(X, Y)}{P_{Y}(Y)} \hspace{0.05cm}, \hspace{0.5cm} P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{P_{XY}(X, Y)}{P_{X}(X)} \hspace{0.05cm}.$$
Analog zur Verbundentropie $H(XY)$ lassen sich hier folgende Entropiefunktionen ableiten:
$\text{Definitionen:}$
- Die bedingte Entropie (englisch: "Conditional Entropy") der Zufallsgröße $X$ unter der Bedingung $Y$ lautet:
- $$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{Y}(y)}{P_{XY}(x, y)} \hspace{0.05cm}.$$
- In gleicher Weise erhält man für die zweite bedingte Entropie:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} \hspace{0.05cm}.$$
Im Argument der Logarithmusfunktion steht stets eine bedingte Wahrscheinlichkeitsfunktion ⇒ $P_{X\hspace{0.03cm}| \hspace{0.03cm}Y}(·)$ bzw. $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(·)$, während zur Erwartungswertbildung die Verbundwahrscheinlichkeit ⇒ $P_{XY}(·)$ benötigt wird.
Für die bedingten Entropien gibt es folgende Begrenzungen:
- Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich Null. Aus $H(X|Y) = 0$ folgt direkt auch $H(Y|X) = 0$. Beides ist nur für disjunkte Mengen $X$ und $Y$ möglich.
- Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese Aussagen sind einleuchtend, wenn man sich bewusst macht, dass man für „Entropie” synonym auch „Unsicherheit” verwenden kann. Denn: Die Unsicherheit bezüglich der Menge $X$ kann nicht dadurch größer werden, dass man $Y$ kennt.
- Außer bei statistischer Unabhängigkeit ⇒ $H(X|Y) = H(X)$ gilt stets $H(X|Y) < H(X)$. Wegen $H(X) ≤ H(XY)$ und $H(Y) ≤ H(XY)$ gilt somit auch $H(X|Y) ≤ H(XY)$ und $H(Y|X) ≤ H(XY)$. Eine bedingte Entropie kann also nie größer werden als die Verbundentropie.
$\text{Beispiel 2:}$ Wir betrachten die Verbundwahrscheinlichkeiten $P_{RS}(·)$ unseres Würfelexperiments, die im letzten Kapitel als $\text{Beispiel 6}$ ermittelt wurden. In der Mitte der folgenden Grafik ist die damals berechnete Verbundwahrscheinlichkeit $P_{RS}(·)$ nochmals angegeben.
Außen sind die beiden bedingten Wahrscheinlichkeitsfunktionen dargestellt:
$\rm Links$ angegeben ist die bedingte Wahrscheinlichkeitsfunktion
- $$P_{S \vert R}(⋅) = P_{SR}(⋅)/P_R(⋅).$$
- Wegen $P_R(R) = \big [1/6, \ 1/6, \ 1/6, \ 1/6, \ 1/6, \ 1/6 \big ]$ steht hier in allen schraffierten Feldern ⇒ $\text{supp}(P_{S\vert R}) = \text{supp}(P_{R\vert S})$ der gleiche Wahrscheinlichkeitswert $1/6$.
- Daraus folgt für die bedingte Entropie:
- $$H(S \hspace{-0.1cm}\mid \hspace{-0.13cm} R) = \hspace{-0.2cm} \sum_{(r, s) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{RS})} \hspace{-0.6cm} P_{RS}(r, s) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}S \hspace{0.03cm} \mid \hspace{0.03cm} R} (s \hspace{-0.05cm}\mid \hspace{-0.05cm} r)} $$
- $$\Rightarrow \hspace{0.3cm}H(S \hspace{-0.1cm}\mid \hspace{-0.13cm} R) = 36 \cdot \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm}.$$
$\rm Rechts$ ist $P_{R\vert S}(⋅) = P_{RS}(⋅)/P_S(⋅)$ angegeben, wobei $P_S(⋅)$ gemäß $\text{Beispiel 6}$ einzusetzen ist.
- Es ergeben sich die gleichen Felder ungleich Null ⇒ $\text{supp}(P_{R\vert S}) = \text{supp}(P_{S\vert R})$.
- Die Wahrscheinlichkeitswerte nehmen nun aber von der Mitte $(1/6)$ zu den Rändern hin bis zur Wahrscheinlichkeit $1$ in den Ecken kontinuierlich zu. Daraus folgt:
- $$H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} S) = \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) + \frac{2}{36} \cdot \sum_{i=1}^5 \big [ i \cdot {\rm log}_2 \hspace{0.1cm} (i) \big ]= 1.896\ {\rm bit} \hspace{0.05cm}.$$
Für die bedingten Wahrscheinlichkeiten der 2D–Zufallsgröße $RB$ gemäß $\text{Beispiel 5}$ erhält man dagegen wegen $P_{RB}(⋅) = P_R(⋅) · P_B(⋅)$:
- $$\begin{align*}H(B \hspace{-0.1cm}\mid \hspace{-0.13cm} R) \hspace{-0.15cm} & = \hspace{-0.15cm} H(B) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm},\\ H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} B) \hspace{-0.15cm} & = \hspace{-0.15cm} H(R) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm}.\end{align*}$$
Transinformation zwischen zwei Zufallsgrößen
Wir betrachten die Zufallsgröße $XY$ mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$. Bekannt seien auch die 1D–Funktionen $P_X(X)$ und $P_Y(Y)$.
Nun stellen sich folgende Fragen:
- Wie vermindert die Kenntnis der Zufallsgröße $Y$ die Unsicherheit bezüglich $X$?
- Wie vermindert die Kenntnis der Zufallsgröße $X$ die Unsicherheit bezüglich $Y$?
Zur Beantwortung benötigen wir eine für die Informationstheorie substantielle Definition:
$\text{Definition:}$ Die Transinformation (englisch: "Mutual Information") zwischen den Zufallsgrößen $X$ und $Y$ – beide über dem gleichen Alphabet – ist wie folgt gegeben:
- $$I(X;\ Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] =\hspace{-0.25cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(x, y)} {P_{X}(x) \cdot P_{Y}(y) } \hspace{0.01cm}.$$
Ein Vergleich mit dem letzten Kapitel zeigt, dass die Transinformation auch als Kullback–Leibler–Distanz zwischen der 2D–PMF $P_{XY}$ und dem Produkt $P_X · P_Y$ geschrieben werden kann:
- $$I(X;Y) = D(P_{XY} \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_X \cdot P_Y) \hspace{0.05cm}.$$
Es ist somit offensichtlich, dass stets $I(X;\ Y) ≥ 0$ gilt. Wegen der Symmetrie ist auch $I(Y;\ X)$ = $I(X;\ Y)$.
Sucht man in einem Wörterbuch die Übersetzung für „mutual”, so findet man unter Anderem die Begriffe „gemeinsam”, „gegenseitig”, „beidseitig” und „wechselseitig”. Und ebenso sind in Fachbüchern für $I(X; Y)$ auch die Bezeichnungen „gemeinsame Entropie” und „'gegenseitige Entropie” üblich. Wir sprechen aber im Folgenden durchgängig von der „Transinformation” $I(X; Y)$ und versuchen nun eine Interpretation dieser Größe:
- Durch Aufspalten des $\log_2$–Arguments entsprechend
- $$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac{1} {P_{X}(X) }\right ] - {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac {P_{Y}(Y) }{P_{XY}(X, Y)} \right ] $$
- erhält man unter Verwendung von $P_{X|Y}(\cdot) = P_{XY}(\cdot)/P_Y(Y)$:
- $$I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) \hspace{0.05cm}.$$
- Das heißt: Die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ vermindert sich bei Kenntnis von $Y$ um den Betrag $H(X|Y)$. Der Rest ist die Transinformation $I(X; Y)$.
- Bei anderer Aufspaltung kommt man zum Ergebnis
- $$I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$
- Ergo: Die Transinformation $I(X; Y)$ ist symmetrisch ⇒ $X$ sagt genau so viel über $Y$ aus wie $Y$ über $X$ ⇒ gegenseitige Information. Das Semikolon weist auf die Gleichberechtigung hin.
$\text{Fazit:}$ Oft werden die hier genannten Gleichungen durch ein Schaubild verdeutlicht, so auch in den folgenden Beispielen. Daraus erkennt man, dass auch folgende Gleichungen zutreffen:
- $$I(X;\ Y) = H(X) + H(Y) - H(XY) \hspace{0.05cm},$$
- $$I(X;\ Y) = H(XY) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$
$\text{Beispiel 3:}$ Wir kommen (letztmalig) auf das Würfel–Experiment mit dem roten $(R)$ und dem blauen $(B)$ Würfel zurück. Die Zufallsgröße $S$ gibt die Summe der beiden Würfel an: $S = R + B$. Wir betrachten hier die 2D–Zufallsgröße $RS$. In früheren Beispielen haben wir berechnet:
- die Entropien $H(R) = 2.585 \ \rm bit$ und $H(S) = 3.274 \ \rm bit$ ⇒ Beispiel 6 im letzten Kapitel,
- die Verbundentropie $H(RS) = 5.170 \ \rm bit$ ⇒ Beispiel 6 im letzten Kapitel,
- die bedingten Entropien $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R) = 2.585 \ \rm bit$ und $H(R \hspace{0.05cm} \vert \hspace{0.05cm} S) = 1.896 \ \rm bit$ ⇒ Beispiel 2 im vorherigen Abschnitt.
Diese Größen sind in der Grafik zusammengestellt, wobei die Zufallsgröße $R$ durch die Grundfarbe „Rot” und die Summe $S$ durch die Grundfarbe „Grün” markiert sind. Bedingte Entropien sind schraffiert. Man erkennt aus dieser Darstellung:
- Die Entropie $H(R) = \log_2 (6) = 2.585\ \rm bit$ ist genau halb so groß wie die Verbundentropie $H(RS)$. Denn: Kennt man $R$, so liefert $S$ genau die gleiche Information wie die Zufallsgröße $B$, nämlich $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R) = H(B) = \log_2 (6) = 2.585\ \rm bit$.
- Hinweis: $H(R)$ = $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ gilt allerdings nicht allgemein, sondern nur in diesem Beispiel.
- Die Entropie $H(S) = 3.274 \ \rm bit$ ist im vorliegenden Beispiel erwartungsgemäß größer als $H(R)= 2.585\ \rm bit$. Wegen $H(S) + H(R \hspace{0.05cm} \vert \hspace{0.05cm} S) = H(R) + H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ muss deshalb $H(R \hspace{0.05cm} \vert \hspace{0.05cm} S)$ gegenüber $H(S \hspace{0.05cm} \vert \hspace{0.05cm} R)$ um den gleichen Betrag $I(R;\ S) = 0.689 \ \rm bit$ kleiner sein als $H(R)$ gegenüber $H(S)$.
- Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $R$ und $S$ ergibt sich aber auch aus der Gleichung
- $$I(R;\ S) = H(R) + H(S) - H(RS) = 2.585\ {\rm bit} + 3.274\ {\rm bit} - 5.170\ {\rm bit} = 0.689\ {\rm bit} \hspace{0.05cm}. $$
Bedingte Transinformation
Wir betrachten nun drei Zufallsgrößen $X$, $Y$ und $Z$, die zueinander in Beziehung stehen (können).
$\text{Definition:}$ Die bedingte Transinformation (englisch: "Conditional Mutual Information") zwischen den Zufallsgrößen $X$ und $Y$ bei gegebenem $Z = z$ lautet:
- $$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z = z) - H(X\vert\hspace{0.05cm}Y ,\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$
Man bezeichnet als die bedingte Transinformation zwischen den Zufallsgrößen $X$ und $Y$ für die Zufallsgröße $Z$ allgemein nach Mittelung über alle $z \in Z$:
- $$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z ) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z ) - H(X\vert\hspace{0.05cm}Y Z )= \hspace{-0.3cm} \sum_{z \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Z})} \hspace{-0.25cm} P_{Z}(z) \cdot I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$
$P_Z(Z)$ ist die Wahrscheinlichkeitsfunktion $\rm (PMF)$ der Zufallsgröße $Z$ und $P_Z(z)$ die Wahrscheinlichkeit für die Realisierung $Z = z$.
$\text{Bitte beachten Sie:}$
- Für die bedingte Entropie gilt bekanntlich die Größenrelation $H(X\hspace{0.05cm}\vert\hspace{0.05cm}Z) ≤ H(X)$.
- Für die Transinformation gilt diese Größenrelation nicht unbedingt:
- $I(X; Y\hspace{0.05cm}\vert\hspace{0.05cm}Z)$ kann kleiner, gleich, aber auch größer sein als $I(X; Y)$.
$\text{Beispiel 4:}$ Wir betrachten die binären Zufallsgrößen $X$, $Y$ und $Z$ mit folgenden Eigenschaften:
- $X$ und $Y$ seien statistisch unabhängig. Für ihre Wahrscheinlichkeitsfunktionen gelte:
- $$P_X(X) = \big [1/2, \ 1/2 \big], \hspace{0.2cm} P_Y(Y) = \big[1– p, \ p \big] \ ⇒ \ H(X) = 1\ {\rm bit}, \hspace{0.2cm} H(Y) = H_{\rm bin}(p).$$
- $Z$ ist die Modulo–2–Summe von $X$ und $Y$: $Z = X ⊕ Y$.
Aus der Verbund–Wahrscheinlichkeitsfunktion $P_{XZ}$ gemäß der oberen Grafik folgt:
- Durch Summation der Spalten–Wahrscheinlichkeiten ergibt sich $P_Z(Z) = \big [1/2, \ 1/2 \big ]$ ⇒ $H(Z) = 1\ {\rm bit}$.
- $X$ und $Z$ sind ebenfalls statistisch unabhängig, da für die 2D–PMF $P_{XZ}(X, Z) = P_X(X) · P_Z(Z)$ gilt.
- Daraus folgt: $H(Z\hspace{0.05cm}\vert\hspace{0.05cm} X) = H(Z)$ und $H(X \hspace{0.05cm}\vert\hspace{0.05cm} Z) = H(X)$ sowie $I(X; Z) = 0$.
Aus der bedingten Wahrscheinlichkeitsfunktion $P_{X\vert YZ}$ gemäß der unteren Grafik lassen sich berechnen:
- $H(X\hspace{0.05cm}\vert\hspace{0.05cm} YZ) = 0$, da alle $P_{X\hspace{0.05cm}\vert\hspace{0.05cm} YZ}$–Einträge entweder $0$ oder $1$ sind ⇒ „bedingte Entropie”,
- $I(X; YZ) = H(X) - H(X\hspace{0.05cm}\vert\hspace{0.05cm} YZ) = H(X)= 1 \ {\rm bit}$ ⇒ „Transinformation”,
- $I(X; Y\vert Z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z) =H(X)=1 \ {\rm bit} $ ⇒ „bedingte Transinformation”.
Im vorliegenden Beispiel ist also
- die bedingte Transinformation $I(X; Y\hspace{0.05cm}\vert\hspace{0.05cm} Z) = 1$
- größer als die herkömmliche Transinformation $I(X; Y) = 0$.
Kettenregel der Transinformation
Bisher haben wir die Transinformation nur zwischen zwei eindimensionalen Zufallsgrößen betrachtet. Nun erweitern wir die Definition auf insgesamt $n + 1$ Zufallsgrößen, die wir aus Darstellungsgründen mit $X_1$, ... , $X_n$ sowie $Z$ bezeichnen. Dann gilt:
$\text{Kettenregel der Transinformation:}$
Die Transinformation zwischen der $n$–dimensionalen Zufallsgröße $X_1 X_2 \hspace{0.05cm}\text{...} \hspace{0.05cm} X_n$ und der Zufallsgröße $Z$ lässt sich wie folgt darstellen und berechnen:
- $$I(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n;Z) = I(X_1;Z) + I(X_2;Z \vert X_1) + \hspace{0.05cm}\text{...} \hspace{0.1cm}+ I(X_n;Z\vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{n-1}) = \sum_{i = 1}^{n} I(X_i;Z \vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \hspace{0.05cm}.$$
$\text{Beweis:}$ Wir beschränken uns hier auf den Fall $n = 2$, also auf insgesamt drei Zufallsgrößen, und ersetzen $X_1$ durch $X$ und $X_2$ durch $Y$. Dann erhalten wir:
- $$\begin{align*}I(X\hspace{0.05cm}Y;Z) & = H(XY) - H(XY\hspace{0.05cm} \vert \hspace{0.05cm}Z) = \\ & = \big [ H(X)+ H(Y\hspace{0.05cm} \vert \hspace{0.05cm} X)\big ] - \big [ H(X\hspace{0.05cm} \vert \hspace{0.05cm} Z) + H(Y\hspace{0.05cm} \vert \hspace{0.05cm} XZ)\big ] =\\ & = \big [ H(X)- H(X\hspace{0.05cm} \vert \hspace{0.05cm} Z)\big ] - \big [ H(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) + H(Y\hspace{0.05cm} \vert \hspace{0.05cm}XZ)\big ]=\\ & = I(X;Z) + I(Y;Z \hspace{0.05cm} \vert \hspace{0.05cm} X) \hspace{0.05cm}.\end{align*}$$
Aus dieser Gleichung erkennt man, dass die die Größenrelation $I(X Y; Z) ≥ I(X; Z)$ immer gegeben ist.
- Gleichheit ergibt sich für die bedingte Transinformation $I(Y; Z \hspace{0.05cm} \vert \hspace{0.05cm} X) = 0$,
- also dann, wenn die Zufallsgrößen $Y$ und $Z$ für ein gegebenes $X$ statistisch unabhängig sind.
$\text{Beispiel 5:}$ Wir betrachten die Markovkette $X → Y → Z$. Für eine solche Konstellation gilt stets das Data Processing Theorem mit der folgenden Konsequenz, die sich aus der Kettenregel der Transinformation ableiten lässt:
- $$I(X;Z) \hspace{-0.05cm} \le \hspace{-0.05cm}I(X;Y ) \hspace{0.05cm},$$
- $$I(X;Z) \hspace{-0.05cm} \le \hspace{-0.05cm} I(Y;Z ) \hspace{0.05cm}.$$
Das Theorem besagt somit:
- Man kann durch Manipulation $($"Processing" $Z)$ der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
- Die Datenverarbeitung $Y → Z$ $($durch einen zweiten Prozessor$)$ dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.
Weitere Informationen zum "Data Processing Theorem" finden Sie in der Aufgabe 3.15.
Aufgaben zum Kapitel
Aufgabe 3.7: Einige Entropieberechnungen
Aufgabe 3.8: Nochmals Transinformation
Aufgabe 3.8Z: Tupel aus ternären Zufallsgrößen
Aufgabe 3.9: Bedingte Transinformation