Aufgaben:Aufgabe 4.6: Quantisierungskennlinien: Unterschied zwischen den Versionen
Aus LNTwww
Safwen (Diskussion | Beiträge) |
|||
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1623__Mod_Z_4_5.png|right|]] | + | [[Datei:P_ID1623__Mod_Z_4_5.png|right|frame|Nichtlineare Quantisierungskennlinien]] |
| − | Es wird die nichtlineare Quantisierung betrachtet und es gilt weiterhin das Systemmodell gemäß [ | + | Es wird die nichtlineare Quantisierung betrachtet und es gilt weiterhin das Systemmodell gemäß [[Aufgaben:4.5_Nichtlineare_Quantisierung| Aufgabe 4.5]]. |
| − | + | ||
| − | $$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} { | + | Die Grafik zeigt zwei Kompressorkennlinien $q_{\rm K}(q_{\rm A})$: |
| − | + | * Rot eingezeichnet ist die sogenannte '''A–Kennlinie''', die vom CCITT ("Comité Consultatif International Téléphonique et Télégraphique") für das Standardsystem PCM 30/32 empfohlen wurde. Für $0 ≤ q_{\rm A} ≤ 1$ gilt hier: | |
| + | :$$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} {{1}/{A} \le q_{\rm A} \le 1} \hspace{0.05cm}, \\ \\ {q_{\rm A} < {1}/{A}} \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | * Der blau–gestrichelte Kurvenzug gilt für die so genannte '''13–Segment–Kennlinie'''. Diese ergibt sich aus der A–Kennlinie durch stückweise Linearisierung; sie wird in der [[Aufgaben:4.5_Nichtlineare_Quantisierung| Aufgabe 4.5]] ausführlich behandelt. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Pulscodemodulation|"Pulscodemodulation"]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Pulscodemodulation#Kompression_und_Expandierung|"Kompression und Expandierung"]]. | ||
| + | *Für die durchgehend rot gezeichnete A-Kennlinie ist der Quantisierungsparameter $A = 100$ gewählt. <br>Mit dem vom CCITT vorgeschlagenen Wert $A = 87.56$ ergibt sich ein ähnlicher Verlauf. | ||
| + | *Für die beiden weiteren Kurven gilt $A = A_1$ (strich–punktierte Kurve) bzw. $A = A_2$ (punktierte Kurve), wobei für $A_1$ bzw. $A_2$ die beiden möglichen Zahlenwerte $50$ und $200$ vorgegeben sind. In der Teilaufgabe '''(3)''' sollen Sie entscheiden, welche Kurve zu welchem Zahlenwert gehört. | ||
| − | |||
| − | |||
| Zeile 23: | Zeile 33: | ||
+ Die Verfälschung kleiner Amplituden ist subjektiv störender. | + Die Verfälschung kleiner Amplituden ist subjektiv störender. | ||
| − | {Welche Unterschiede gibt es zwischen der | + | {Welche Unterschiede gibt es zwischen der A–Kennlinie und der 13–Segment–Kennlinie? |
|type="[]"} | |type="[]"} | ||
+ Die A–Kennlinie beschreibt einen kontinuierlichen Verlauf. | + Die A–Kennlinie beschreibt einen kontinuierlichen Verlauf. | ||
| − | + Die | + | + Die 13–Segment–Kurve nähert die A–Kennlinie stückweise linear an. |
- Bei der Realisierung zeigt die A–Kennlinie wesentliche Vorteile. | - Bei der Realisierung zeigt die A–Kennlinie wesentliche Vorteile. | ||
| − | {Lässt sich allein aus $ | + | {Lässt sich allein aus $q_{\rm A} = 1$ ⇒ $q_{\rm K} = 1$ der Parameter $A$ ableiten? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Ja. |
| − | + | + | + Nein. |
| − | {Lässt sich A bestimmen, wenn man vorgibt, dass der Übergang zwischen den beiden Bereichen kontinuierlich sein soll? | + | {Lässt sich $A$ bestimmen, wenn man vorgibt, dass der Übergang zwischen den beiden Bereichen kontinuierlich sein soll? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Ja. |
| − | + | + | + Nein. |
| − | {Bestimmen Sie A aus der Bedingung $ | + | {Bestimmen Sie $A$ aus der Bedingung $q_{\rm K}(q_{\rm A} = 1/2) = 0.8756$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A \ = \ $ { 94 3% } |
| − | {Welche Parameterwerte | + | {Welche Parameterwerte wurden für die weiteren Kurven verwendet? |
| − | |type=" | + | |type="()"} |
| − | - Es gilt $A_1 = 50$ und $A_2 = 200$. | + | - Es gilt $A_1 = 50$ und $A_2 = 200$. |
| − | + Es gilt $A_1 = 200$ und $A_2 = 50$. | + | + Es gilt $A_1 = 200$ und $A_2 = 50$. |
| Zeile 56: | Zeile 66: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | |
| − | $$ | + | '''(1)''' Richtig sind die <u>Aussagen 2 und 3</u>: |
| − | + | *Eine Signalverfälschung von leisen Tönen oder in Sprachpausen wird subjektiv als störender empfunden als zum Beispiel ein zusätzliches Geräusch bei Heavy Metal. | |
| + | *Bezüglich des Quantisierungsrauschens bzw. des SNR gibt es durch eine nichtlineare Quantisierung allerdings keine Verbesserung, wenn von einer Gleichverteilung der Amplitudenwerte ausgegangen wird. | ||
| + | *Berücksichtigt man aber, dass bei Sprach– und Musiksignalen kleinere Amplituden sehr viel häufiger auftreten als große ⇒ "Laplaceverteilung", so ergibt sich durch die nichtlineare Quantisierung auch ein besseres SNR. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Richtig sind die <u>Aussagen 1 und 2</u>: | ||
| + | *Durch die Linearisierung in den einzelnen Segmenten ist in diesen bei der 13–Segment–Kennlinie die Intervallbreite der verschiedenen Quantisierungsstufen konstant, was sich bei der Realisierung günstig auswirkt. | ||
| + | *Dagegen gibt es bei der nichtlinearen Quantisierung gemäß der A–Kennlinie keine Quantisierungsintervalle gleicher Breite. Das bedeutet: Die Aussage 3 ist falsch. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist "<u>NEIN</u>": | ||
| + | *Für $q_{\rm A} = 1$ erhält man unabhängig von $A$ den Wert $q_{\rm K} = 1$. | ||
| + | *Allein mit dieser Vorgabe kann $A$ also nicht ermittelt werden. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Richtig ist wiederum "<u>NEIN</u>": | ||
| + | *Für $q_{\rm A} = 1/A$ liefern beide Bereichsgleichungen den gleichen Wert $q_{\rm K}= 1/[1 + \ln(A)]$. | ||
| + | *Auch damit kann $A$ nicht bestimmt werden. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Mit dieser Forderung ist $A$ nun berechenbar: | ||
| + | :$$0.875 = \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A/2)} {1 | ||
| + | \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} = | ||
| + | \frac{1\hspace{0.05cm}-\hspace{0.05cm} {\rm ln}(2) | ||
| + | \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A)} {1 \hspace{0.05cm}+ | ||
| + | \hspace{0.05cm}{\rm ln}(A )}\approx \frac{1-0.693 | ||
| + | \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A)} {1 \hspace{0.05cm}+ | ||
| + | \hspace{0.05cm}{\rm ln}(A )}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}{\rm ln}(A) = \frac{0.875 - 0.307 } {1 | ||
| + | -0.875 }= 4.544 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A \hspace{0.15cm}\underline {\approx | ||
| + | 94} \hspace{0.05cm}.$$ | ||
| + | |||
| − | ''' | + | '''(6)''' Richtig ist die <u>Aussage 2</u>: |
| − | $ | + | *Die Kurve für $A_1 = 200$ liegt oberhalb der Kurve mit $A = 100$, die Kurve mit $A_2 = 50$ unterhalb. |
| − | + | *Dies zeigt die folgende Rechnung, gültig für $q_{\rm A} = 0.5$: | |
| − | + | :$$A= 100\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1 + \ln(100) - \ln(2)}{1 + \ln(100)}= | |
| − | + | \frac{1+4.605- 0.693} {1 +4.605}\approx | |
| − | $$\ | + | 0.876 \hspace{0.05cm},$$ |
| − | + | :$$A= 200\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1+5.298- 0.693} {1 +5.298}\approx | |
| + | 0.890 \hspace{0.05cm},$$ | ||
| + | :$$A= 50\text{:}\hspace{0.4cm} q_{\rm K}= \frac{1+3.912- 0.693} {1 +3.912}\approx | ||
| + | 0.859 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 10. April 2022, 10:36 Uhr
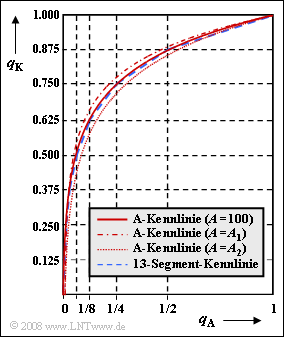
Es wird die nichtlineare Quantisierung betrachtet und es gilt weiterhin das Systemmodell gemäß Aufgabe 4.5.
Die Grafik zeigt zwei Kompressorkennlinien $q_{\rm K}(q_{\rm A})$:
- Rot eingezeichnet ist die sogenannte A–Kennlinie, die vom CCITT ("Comité Consultatif International Téléphonique et Télégraphique") für das Standardsystem PCM 30/32 empfohlen wurde. Für $0 ≤ q_{\rm A} ≤ 1$ gilt hier:
- $$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} {{1}/{A} \le q_{\rm A} \le 1} \hspace{0.05cm}, \\ \\ {q_{\rm A} < {1}/{A}} \hspace{0.05cm}. \\ \end{array}$$
- Der blau–gestrichelte Kurvenzug gilt für die so genannte 13–Segment–Kennlinie. Diese ergibt sich aus der A–Kennlinie durch stückweise Linearisierung; sie wird in der Aufgabe 4.5 ausführlich behandelt.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Pulscodemodulation".
- Bezug genommen wird insbesondere auf die Seite "Kompression und Expandierung".
- Für die durchgehend rot gezeichnete A-Kennlinie ist der Quantisierungsparameter $A = 100$ gewählt.
Mit dem vom CCITT vorgeschlagenen Wert $A = 87.56$ ergibt sich ein ähnlicher Verlauf. - Für die beiden weiteren Kurven gilt $A = A_1$ (strich–punktierte Kurve) bzw. $A = A_2$ (punktierte Kurve), wobei für $A_1$ bzw. $A_2$ die beiden möglichen Zahlenwerte $50$ und $200$ vorgegeben sind. In der Teilaufgabe (3) sollen Sie entscheiden, welche Kurve zu welchem Zahlenwert gehört.
Fragebogen
Musterlösung
(1) Richtig sind die Aussagen 2 und 3:
- Eine Signalverfälschung von leisen Tönen oder in Sprachpausen wird subjektiv als störender empfunden als zum Beispiel ein zusätzliches Geräusch bei Heavy Metal.
- Bezüglich des Quantisierungsrauschens bzw. des SNR gibt es durch eine nichtlineare Quantisierung allerdings keine Verbesserung, wenn von einer Gleichverteilung der Amplitudenwerte ausgegangen wird.
- Berücksichtigt man aber, dass bei Sprach– und Musiksignalen kleinere Amplituden sehr viel häufiger auftreten als große ⇒ "Laplaceverteilung", so ergibt sich durch die nichtlineare Quantisierung auch ein besseres SNR.
(2) Richtig sind die Aussagen 1 und 2:
- Durch die Linearisierung in den einzelnen Segmenten ist in diesen bei der 13–Segment–Kennlinie die Intervallbreite der verschiedenen Quantisierungsstufen konstant, was sich bei der Realisierung günstig auswirkt.
- Dagegen gibt es bei der nichtlinearen Quantisierung gemäß der A–Kennlinie keine Quantisierungsintervalle gleicher Breite. Das bedeutet: Die Aussage 3 ist falsch.
(3) Richtig ist "NEIN":
- Für $q_{\rm A} = 1$ erhält man unabhängig von $A$ den Wert $q_{\rm K} = 1$.
- Allein mit dieser Vorgabe kann $A$ also nicht ermittelt werden.
(4) Richtig ist wiederum "NEIN":
- Für $q_{\rm A} = 1/A$ liefern beide Bereichsgleichungen den gleichen Wert $q_{\rm K}= 1/[1 + \ln(A)]$.
- Auch damit kann $A$ nicht bestimmt werden.
(5) Mit dieser Forderung ist $A$ nun berechenbar:
- $$0.875 = \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A/2)} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} = \frac{1\hspace{0.05cm}-\hspace{0.05cm} {\rm ln}(2) \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A)} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )}\approx \frac{1-0.693 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A)} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm ln}(A) = \frac{0.875 - 0.307 } {1 -0.875 }= 4.544 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A \hspace{0.15cm}\underline {\approx 94} \hspace{0.05cm}.$$
(6) Richtig ist die Aussage 2:
- Die Kurve für $A_1 = 200$ liegt oberhalb der Kurve mit $A = 100$, die Kurve mit $A_2 = 50$ unterhalb.
- Dies zeigt die folgende Rechnung, gültig für $q_{\rm A} = 0.5$:
- $$A= 100\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1 + \ln(100) - \ln(2)}{1 + \ln(100)}= \frac{1+4.605- 0.693} {1 +4.605}\approx 0.876 \hspace{0.05cm},$$
- $$A= 200\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1+5.298- 0.693} {1 +5.298}\approx 0.890 \hspace{0.05cm},$$
- $$A= 50\text{:}\hspace{0.4cm} q_{\rm K}= \frac{1+3.912- 0.693} {1 +3.912}\approx 0.859 \hspace{0.05cm}.$$