Digitalsignalübertragung/Trägerfrequenzsysteme mit nichtkohärenter Demodulation: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
|||
| (30 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
| − | == Rayleigh– und Riceverteilung | + | == Rayleigh– und Riceverteilung == |
<br> | <br> | ||
| − | Die für eine kohärente Demodulation erforderliche Schätzung des Phasenwinkels aus dem ankommenden Signal ist bei vielen Anwendungen nicht oder nur eingeschränkt möglich. So führt die Bewegung eines Mobilteilnehmers mit hoher Geschwindigkeit zu sehr schnellen zeitlichen Änderungen des Phasenwinkels | + | Die für eine kohärente Demodulation erforderliche Schätzung des Phasenwinkels aus dem ankommenden Signal ist bei vielen Anwendungen nicht oder nur eingeschränkt möglich. So führt die Bewegung eines Mobilteilnehmers mit hoher Geschwindigkeit zu sehr schnellen zeitlichen Änderungen des Phasenwinkels $\phi$, was dessen ausreichend genaue Bestimmung erschwert oder gar verhindert.<br> |
| − | Diese Tatsache führt zu den nichtkohärenten Demodulationsverfahren mit dem Vorteil reduzierter Komplexität, allerdings mit erhöhter Verfälschungswahrscheinlichkeit. Bei der Herleitung der Gleichungen stößt man auf zwei Wahrscheinlichkeitsdichtefunktionen, die hier vorneweg angegeben werden: | + | Diese Tatsache führt zu den '''nichtkohärenten Demodulationsverfahren''' mit dem Vorteil reduzierter Komplexität, allerdings mit erhöhter Verfälschungswahrscheinlichkeit. Bei der Herleitung der Gleichungen stößt man auf zwei Wahrscheinlichkeitsdichtefunktionen, die hier vorneweg angegeben werden: |
| − | *Die Rayleighverteilung erhält man für die WDF der Zufallsgröße | + | |
| + | *Die [[Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung|'''Rayleighverteilung''']] erhält man für die WDF der Zufallsgröße $y$ mit Realisierung $\eta$, die sich aus den beiden gaußverteilten und statistisch unabhängigen Komponenten $u$ und $v$ $($beide mit der gleichen Streuung $\sigma_n)$ wie folgt ergibt: | ||
::<math>y = \sqrt{u^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) ={\eta}/{\sigma_n^2} | ::<math>y = \sqrt{u^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) ={\eta}/{\sigma_n^2} | ||
| Zeile 17: | Zeile 18: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Die Riceverteilung erhält man unter | + | *Die [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung|'''Riceverteilung''']] erhält man unter gleichen Randbedingungen für den Fall, dass bei einer der Komponenten $(u$ oder $v)$ noch eine Konstante $C$ addiert wird: |
::<math>y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = {\eta}/{\sigma_n^2} | ::<math>y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = {\eta}/{\sigma_n^2} | ||
| Zeile 23: | Zeile 24: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | :Die Riceverteilung verwendet die "modifizierte Besselfunktion nullter Ordnung", deren Definition und Reihenentwicklung wie folgt lauten: | |
| − | + | ::<math>{\rm I }_0 (x) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{-x \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} \approx \hspace{0.2cm} | |
| − | :<math>{\rm I }_0 (x) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{-x \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} \approx \hspace{0.2cm} | ||
\sum_{k = 0}^{\infty} \frac{(x/2)^{2k}}{k! \cdot \Gamma (k+1)} | \sum_{k = 0}^{\infty} \frac{(x/2)^{2k}}{k! \cdot \Gamma (k+1)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | Die Grafik zeigt die Wahrscheinlichkeitsdichtefunktionen von Rayleigh– und Riceverteilung. Zu dieser Darstellung ist anzumerken: | ||
| − | + | [[Datei:P ID2082 Dig T 4 5 S1 version1_ret.png|right|frame|Rayleigh- und Rice-WDF, jeweils für $σ_n = 0.5$|class=fit]] | |
| − | |||
| − | [[Datei:P ID2082 Dig T 4 5 S1 | ||
| − | + | *Die Riceverteilung ist durch die beiden Parameter $C$ und $\sigma_n$ bestimmt. Mit $C = 0$ ist die Rice–WDF identisch mit der Rayleigh–WDF.<br> | |
| − | |||
| − | |||
| − | *Die | ||
| − | *Die Rayleigh–WDF mit größerem | + | *Die Rayleigh–WDF mit größerem $\sigma_n$ ist formgleich wie für $\sigma_n = 0.5$ dargestellt, aber im Verhältnis der Streuungen breiter und niedriger.<br> |
| − | * | + | *$\sigma_n$ gibt die Streuung der beiden gaußverteilten Zufallsgrößen $u$ und $v$ an und nicht die Streuung der rayleighverteilten Zufallsgröße $y$. Diese ist: |
::<math>\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n | ::<math>\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Die Rayleighverteilung ist extrem unsymmetrisch, erkennbar am | + | *Die Rayleighverteilung ist extrem unsymmetrisch, erkennbar am großen Wert für das [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Einige_h.C3.A4ufig_benutzte_Zentralmomente|"Zentralmoment 3. Ordnung"]] ⇒ "Charliersche Schiefe": |
| + | :$$\mu_3/\sigma_y \approx 0.27.$$ | ||
| − | *Die Riceverteilung ist um so symmetrischer, je größer das Verhältnis | + | *Die Riceverteilung ist um so symmetrischer, je größer das Verhältnis von Mittelwert und Streuung $(C/\sigma_n)$ ist. Für $C/\sigma_n \ge 4$ ist $\mu_3 \approx 0$. |
| − | * | + | *Je größer $C/\sigma_n$ ist, um so mehr nähert sich die Riceverteilung $($mit $C$, $\sigma_n)$ einer [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion|Gaußverteilung]] mit Mittelwert $C$ und Streuung $\sigma_n$ an: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [ | + | :$$p_y (\eta) \approx \frac{1}{\sqrt{2\pi} \cdot \sigma_n} |
| + | \cdot {\rm exp } \left [ - \frac{(\eta - C)^2}{2 \sigma_n^2}\right ]$$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm} m_y = C\hspace{0.05cm},\hspace{0.2cm}\sigma_y = \sigma_n | ||
| + | \hspace{0.05cm}.$$ | ||
| − | == Nichtkohärente Demodulation von On–Off–Keying | + | == Nichtkohärente Demodulation von On–Off–Keying== |
<br> | <br> | ||
| − | Wir betrachten [ | + | Wir betrachten [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|"On–Off–Keying"]] $\rm (OOK)$ bzw. $\rm 2–ASK)$ im äquivalenten Tiefpassbereich. |
| + | |||
| + | [[Datei:P ID2083 Dig T 4 5 S2a version1.png|right|frame|Kohärente und nichtkohärente Demodulation von On-Off-Keying|class=fit]] | ||
| − | + | *Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals $\boldsymbol{r}(t)$ gleich der des Sendesignals $\boldsymbol{s}(t)$ und besteht aus zwei Punkten (linke Grafik). | |
| + | |||
| + | *Die Entscheidungsgrenze $G$ liegt in der Mitte zwischen diesen Punkten $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$. Die Pfeile markieren die grobe Richtung von Rauschvektoren, die eventuell zu Übertragungsfehlern führen. | ||
| − | |||
| − | |||
| − | *Dagegen kann | + | Dagegen gilt bei nichtkohärenter Demodulation (rechte Grafik): |
| + | *Der Punkt $\boldsymbol{r}_1 = \boldsymbol{s}_1 = 0$ bleibt weiter erhalten. Dagegen kann $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ auf jeden Punkt des Kreises um $\boldsymbol{s}_0$ liegen, da $\phi$ unbekannt ist.<br> | ||
| − | *Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun | + | *Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun zweidimensional zu interpretieren, wie durch die Pfeile in der rechten Grafik angedeutet.<br> |
| − | *Das Entscheidungsgebiet | + | *Das Entscheidungsgebiet $I_1$ ist ein Kreis, dessen Radius $G$ ein optimierbarer Parameter ist. Das Entscheidungsgebiet $I_0$ liegt außerhalb des Kreises.<br> |
| − | |||
| − | [[Datei:P ID3147 Dig T 4 5 S2b version1.png|Empfänger für nichtkohärente OOK-Demodulation|class=fit]] | + | Damit liegt die Strukur des optimalen OOK–Empfängers (im äquivalenten Tiefpassbereich) fest. Entsprechend dieser zweiten Grafik gilt: |
| + | [[Datei:P ID3147 Dig T 4 5 S2b version1.png|right|frame|Empfänger für nichtkohärente OOK-Demodulation (komplexen Signale sind blau beschriftet)|class=fit]] | ||
| + | *Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ ist aufgrund des Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex. | ||
| − | + | * Erforderlich ist demzufolge nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}_1(t)$.<br> | |
| − | |||
| − | |||
| − | * | ||
| − | * | + | *Das Ergebnis ist der (komplexe) Detektorausgangswert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.<br> |
| − | * | + | *Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$. |
| − | * | + | *Die Fehlerwahrscheinlichkeit ist bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}(\boldsymbol{m}_0) = {\rm Pr}(\boldsymbol{m}_1) =1/2$ : |
| − | ::<math>p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y | + | ::<math>p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}|\hspace{0.05cm} m_0) \,{\rm d} \eta |
| − | + {1}/{ 2} \cdot \int_{G}^{\infty} p_{y | + | + {1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} m_1) \,{\rm d} \eta |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Aufgrund der Rice–WDF | + | *Aufgrund der Rice –WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_0)$ und der Rayleigh–WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_1)$ kann allerdings diese Wahrscheinlichkeit nur numerisch ermittelt werden. |
| − | ::<math>p_{y | + | |
| + | *Die optimale Entscheidungsgrenze $G$ ist vorher als die Lösung der folgenden Gleichung zu bestimmen: | ||
| + | ::<math>p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_0) = p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_1) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | {{GraueBox|TEXT= | ||
| + | [[Datei:P ID3148 Dig T 4 5 S2c version1.png|right|frame|Dichtefunktionen für „OOK, nichtkohärent”]] | ||
| + | $\text{Beispiel 1:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_n = 0.5$ und $C = 2$, wobei die (rote) Rice–WDF durch eine Gauß–WDF mit Mittelwert $C$ und Streuung $\sigma_n$ approximiert ist. | ||
| − | |||
| − | + | Man erkennt daraus: | |
| + | *Die optimale Entscheidungsgrenze $($hier: $G \approx 1.25)$ ergibt sich aus dem Schnittpunkt der beiden Kurven.<br> | ||
| − | *Die | + | *Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. |
| − | * | + | *Im Beispiel ergibt sich $p_{\rm S} \approx 5\%$. |
| − | Die Fehlerwahrscheinlichkeit für andere Werte von | + | ⇒ Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem HTML5/JavaScript–Berechnungstool [[Applets:Kohärentes_und_inkohärentes_On-Off-Keying|"Nichtkohärentes On–Off–Keying"]] bestimmen.}} |
| − | == Nichtkohärente Demodulation von binärer FSK ( | + | == Nichtkohärente Demodulation von binärer FSK (2–FSK)== |
<br> | <br> | ||
| − | Wie schon im [ | + | Wie schon im [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#Binary_Frequency_Shift_Keying_.282.E2.80.93FSK.29| "letzten Kapitel"]] gezeigt wurde, lässt sich "Binary Frequency Shift Keying" $\rm (2–FSK)$ im äquivalenten Tiefpassbereich durch die Basisfunktionen |
| − | + | ::<math>\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},</math> | |
| − | :<math>\xi_1(t) | + | ::<math> \xi_2(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}</math> |
| − | :<math> \xi_2(t) | ||
| − | darstellen. Um Orthogonalität zwischen diesen beiden komplexen Basisfunktionen zu erreichen, muss der [ | + | darstellen. Um Orthogonalität zwischen diesen beiden komplexen Basisfunktionen zu erreichen, muss der [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#Binary_Frequency_Shift_Keying_.282.E2.80.93FSK.29| "Modulationsindex"]] $h$ ganzzahlig gewählt werden: |
| − | :<math>< \hspace{-0.05cm}\xi_1(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0 | + | ::<math>< \hspace{-0.05cm}\xi_1(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0 |
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T\hspace{0.05cm}= 1, 2, 3, ...</math> | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T\hspace{0.05cm}= 1, 2, 3, \text{...}</math> |
Die Grafik zeigt die Struktur zur nichtkohärenten orthogonalen Demodulation der binären FSK.<br> | Die Grafik zeigt die Struktur zur nichtkohärenten orthogonalen Demodulation der binären FSK.<br> | ||
| − | [[Datei:P ID2087 Dig T 4 5 S3a version2.png|Nichtkohärente Demodulation der binären FSK|class=fit]] | + | [[Datei:P ID2087 Dig T 4 5 S3a version2.png|right|frame|Nichtkohärente Demodulation der binären FSK|class=fit]] |
| − | |||
| − | |||
| − | + | Im rauschfreien Fall ⇒ $n(t) \equiv 0$ gilt für die Ausgänge der beiden Korrelatoren: | |
| − | : | ||
| − | + | ::<math>r_1 = \hspace{0.2cm} < \hspace{-0.05cm}r(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_1(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0\hspace{0.05cm}, \hspace{0.2cm} {\rm falls}\hspace{0.25cm} m = m_1\hspace{0.05cm},</math> | |
| + | ::<math> r_2 = \hspace{0.2cm} < \hspace{-0.05cm}r(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0\hspace{0.05cm}, \hspace{0.2cm} {\rm falls}\hspace{0.25cm} m = m_0\hspace{0.05cm}.</math> | ||
| − | :<math>\hat{m} = | + | Nach jeweiliger Betragsbildung ⇒ $y_1 = |r_1|, \ \ y_2 = |r_2|$ ist dann folgende Entscheidungsregel anwendbar: |
| + | ::<math>\hat{m} = | ||
\left\{ \begin{array}{c} m_0 \\ | \left\{ \begin{array}{c} m_0 \\ | ||
m_1 \end{array} \right.\quad | m_1 \end{array} \right.\quad | ||
| Zeile 137: | Zeile 136: | ||
\\ {\rm falls}\hspace{0.15cm} y_1 < y_2 \hspace{0.05cm}.\\ \end{array}</math> | \\ {\rm falls}\hspace{0.15cm} y_1 < y_2 \hspace{0.05cm}.\\ \end{array}</math> | ||
| − | Zur einfacheren | + | Zur einfacheren Entscheiderrealisierung kann auch die Differenz $y_1 - y_2$ mit der Entscheidungsgrenze $G = 0$ ausgewertet werden.<br> |
| − | Im Folgenden wird die Fehlerwahrscheinlichkeit unter der Annahme berechnet, dass | + | == Fehlerwahrscheinlichkeit bei nichtkohärenter 2–FSK–Demodulation== |
| + | <br> | ||
| + | Im Folgenden wird die Fehlerwahrscheinlichkeit unter der Annahme berechnet, dass $m = m_0$ gesendet wurde. | ||
| − | : | + | *Unter der weiteren Voraussetzung gleichwahrscheinlicher binärer Nachrichten $m_0$ und $m_1$ ist die absolute Fehlerwahrscheinlichkeit genau so groß: |
| − | \hspace{0.05cm}. | + | :$${\rm Pr}({\cal{E}}) = {\rm Pr}({\cal{E}}\hspace{0.05cm} | \hspace{0.05cm}m_0) |
| + | \hspace{0.05cm}.$$ | ||
| − | Mit | + | *Mit $m = m_0$ ergeben sich für die komplexen Korrelationsausgangswerte $r_i$ und deren Beträge $y_i$:<br> |
| − | + | ::<math>r_1 = \sqrt{E} \cdot {\rm e}^{{\rm j}\phi} + n_1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_1 = |r_1|\hspace{0.15cm}{\rm ist}\hspace{0.15cm}{\rm riceverteilt} | |
| − | :<math>r_1 | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | :<math> r_2 | + | ::<math> r_2 = n_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_2 = |r_2|\hspace{0.15cm}{\rm ist}\hspace{0.15cm}{\rm rayleighverteilt} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Hierbei steht | + | *Hierbei steht $E$ wegen $M = 2$ für die "mittlere Symbolenergie" $(E_{\rm S})$ und diedie "mittlere Bitenergie" $(E_{\rm B})$ gleichermaßen. $n_1$ und $n_2$ sind unkorrelierte komplexe Rauschgrößen mit Mittelwert Null und Varianz $2 \cdot \sigma_n^2$. Somit lautet die [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#Verbundwahrscheinlichkeitsdichtefunktion|"Verbundwahrscheinlichkeitsdichtefunktion"]]: |
| − | + | ::<math>p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = | |
| − | |||
| − | |||
| − | Somit lautet die Verbundwahrscheinlichkeitsdichtefunktion: | ||
| − | |||
| − | :<math>p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = | ||
p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot | p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot | ||
p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) | p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | + | ::$$p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} | |
| − | : | ||
\cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E}}/{ \sigma_n^2}\right ] | \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E}}/{ \sigma_n^2}\right ] | ||
| − | \hspace{0.05cm}, | + | \hspace{0.05cm},$$ |
| + | ::$$ p_{y_2 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} | ||
| + | \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$ | ||
| − | : | + | *Die Fehlerwahrscheinlichkeit ergibt sich allgemein wie folgt: |
| − | |||
| − | + | ::<math>{\rm Pr}({\cal{E}}) = \int_{0}^{\infty} \int_{\eta_1}^{\infty} | |
| − | + | p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) \,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} | |
| − | :<math>{\rm Pr}({\cal{E}}) | ||
| − | p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) \,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 = | ||
| − | |||
p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 | p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Fazit:}$ Für die '''Fehlerwahrscheinlichkeit bei nichtkohärenter Demodulation der binären FSK''' erhält man nach einigen mathematischen Umformungen das überraschend einfache Ergebnis | ||
| − | :<math>p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} | + | ::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Zum Vergleich sei nochmals das Ergebnis für die kohärente Demodulation angegeben: | + | *Zum Vergleich sei nochmals das Ergebnis für die '''kohärente Demodulation''' angegeben: |
| + | ::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q}(\sqrt{ E_{\rm S}/N_0}) | ||
| + | \hspace{0.05cm}.</math>}} | ||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Herleitung:}$ Das vorweg genommene Ergebnis soll nun in einigen Rechenschritten hergeleitet werden. Wir gehen dabei von den folgenden Gleichungen aus: | ||
| − | [ | + | :$${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} |
| + | p_{y_2 \hspace{0.03cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 | ||
| + | \hspace{0.05cm},\hspace{0.5cm}\text{mit}$$ | ||
| + | ::$$p_{y_1 \hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ] \hspace{0.05cm},$$ | ||
| + | ::$$p_{y_\hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$ | ||
| − | + | <b>(1)</b> Das innere Integral gibt die Wahrscheinlichkeit an, dass die rayleighverteilte Zufallsgröße $\eta_2$ größer ist als $\eta_1$ – siehe Musterlösung zur [[Aufgaben:Aufgabe_4.17Z:_Rayleigh-_und_Riceverteilung|"Aufgabe 4.17Z"]]: | |
| − | |||
| − | + | :$$\int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}\vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2 = | |
| − | + | {\rm e }^{ - \eta_1^2 /({2 \sigma_n^2}) } \hspace{0.3cm} | |
| − | + | \Rightarrow \hspace{0.3cm} {\rm Pr}({\cal{E} }) = \int_{0}^{\infty}{\eta_1}/{\sigma_n^2} | |
| − | |||
| − | |||
| − | |||
| − | : | ||
| − | p_{y_2 \hspace{0.03cm} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\cdot {\rm e }^{ - ({2\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 | \cdot {\rm e }^{ - ({2\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 | ||
| − | \left [ {\eta_1 \cdot \sqrt{E}}/{ \sigma_n^2}\right ]\,\,{\rm d} \eta_1 | + | \left [ {\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ]\,\,{\rm d} \eta_1 |
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | <b>(2)</b> Mit den (willkürlichen) Substitutionen | + | <b>(2)</b> Mit den (willkürlichen) Substitutionen $C_0^2 = E/4$ und $\sigma_0^2 = \sigma_n^2/2$, erhält man: |
| − | : | + | :$${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} |
\cdot {\rm exp } \left [ - \frac{2 \eta_1^2 + 4 C_0^2}{4 \sigma_0^2}\right ] \cdot {\rm I }_0 | \cdot {\rm exp } \left [ - \frac{2 \eta_1^2 + 4 C_0^2}{4 \sigma_0^2}\right ] \cdot {\rm I }_0 | ||
| − | \left [ \frac{\eta_1 \cdot 2C_0}{ 2 \sigma_0^2}\right ]\,\,{\rm d} \eta_1 = | + | \left [ \frac{\eta_1 \cdot 2C_0}{ 2 \sigma_0^2}\right ]\,\,{\rm d} \eta_1 = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} |
| − | |||
\cdot {\rm exp } \left [ - \frac{\eta_1^2 + 2 C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 | \cdot {\rm exp } \left [ - \frac{\eta_1^2 + 2 C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 | ||
\left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 | \left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 | ||
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | <b>(3)</b> Durch Verschieben von Anteilen vor das Integral gelingt es, dass der Integrand wieder eine Riceverteilung beschreibt: | + | <b>(3)</b> Durch Verschieben von Anteilen vor das Integral gelingt es, dass der Integrand wieder eine [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung|Riceverteilung]] beschreibt: |
| − | :<math>{\rm Pr}({\cal{E}}) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] \cdot \int\limits_{0}^{\infty} \frac{\eta_1}{ \sigma_0^2} | + | ::<math>{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] \cdot \int\limits_{0}^{\infty} \frac{\eta_1}{ \sigma_0^2} |
\cdot {\rm exp } \left [ - \frac{\eta_1^2 + C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 | \cdot {\rm exp } \left [ - \frac{\eta_1^2 + C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 | ||
\left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 | \left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(4)</b> Der Integrand beschreibt nun die Rice–WDF. Das Integral über das gesamte Definitionsgebiet von 0 bis +& | + | <b>(4)</b> Der Integrand beschreibt nun die Rice–WDF. Das Integral über das gesamte Definitionsgebiet von $0$ bis $+\infty$ ergibt wie bei jeder WDF den Wert Eins, so dass gilt: |
| + | |||
| + | ::<math>{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ]\hspace{0.05cm}.</math> | ||
| + | |||
| + | <b>(5)</b> Mit $C_0^2 = E/4$ und $\sigma_0^2 = \sigma_n^2/2$ sowie der allgemein gültigen Beziehung $\sigma_n^2 = N_0$ erhält man schließlich: | ||
| + | :$${\rm Pr}({\cal{E} }) | ||
| + | = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] = {1}/{2} \cdot {\rm exp } \left [ - \frac{ E_{\rm S}/4}{N_{\rm 0}/2}\right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)}\hspace{0.05cm}.$$ | ||
| + | $E_{\rm S}$ gibt hierbei die mittlere Signalenergie pro Symbol an, die bei FSK gleich der Normierungsenergie $E$ ist. | ||
| + | <div align="right">$\text{q.e.d.}$</div>}}<br> | ||
| − | : | + | {{GraueBox|TEXT= |
| + | [[Datei:P ID2088 Dig T 4 5 S3b version1.png|right|frame|FSK-Fehlerwahrscheinlichkeit bei kohärenter und nichtkohärenter Demodulation|class=fit]] | ||
| + | $\text{Beispiel 2:}$ Die Grafik stellt die Fehlerwahrscheinlichkeitskurven beider Demodulationsverfahren in Abhängigkeit des AWGN–Qotienten $E_{\rm S}/N_0$ vergleichend gegenüber. | ||
| + | <br><br> | ||
| + | Man erkennt: | ||
| + | #Die nichtkohärente BFSK (rote Kurve) benötigt gegenüber der kohärenten BFSK (blaue Kurve) bei $p_{\rm S}= 10^{-5}$ ein um $0.8 \ \rm dB$ größeres $E_{\rm S}/N_0$.<br><br> | ||
| + | #Bei $p_{\rm S}= 10^{-3}$ beträgt der Abstand sogar $1.3 \ \rm dB$.<br><br> | ||
| + | #Dagegen beträgt der Abstand zwischen der kohärenten binären FSK von der kohärenten BPSK unabhängig von der Fehlerwahrscheinlichkeit stets $1.3 \ \rm dB$. | ||
| + | <br clear =all>}} | ||
| − | |||
| − | + | == Nichtkohärente Demodulation von mehrstufiger FSK== | |
| − | + | <br> | |
| − | + | [[Datei:P ID2089 Dig T 4 5 S4a version1.png|right|frame|Orthogonale $M$–stufige FSK für $M= 3$]] | |
| − | + | Wir betrachten nun die Nachrichtenmenge $\{m_1, m_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, m_{M}\}$ und bezeichnen $M$ als Stufenzahl. | |
| + | #Voraussetzung für die Anwendung des Modulationsverfahrens "Frequency Shift Keying" und zugleich eines nichtkohärenten Demodulators ist wie bei der binären FSK ein ganzzahliger Modulationsindex $h$.<br><br> | ||
| + | #In diesem Fall ist die $M$–stufige FSK orthogonal und es ergibt sich eine Signalraumkonstellation, wie in der nebenstehenden Grafik für den Sonderfall $M = 3$ dargestellt.<br><br> | ||
| − | + | Der nichtkohärente Demodulator ist nachfolgend skizziert. | |
| − | + | *Gegenüber der [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_bin.C3.A4rer_FSK_.282.E2.80.93FSK.29| "Empfängerstruktur für binäre FSK"]] unterscheidet sich dieser Empfänger lediglich durch $M$ Zweige anstelle von nur zweien, welche die Vergleichswerte $y_1$, $y_2$, ... , $y_M$ liefern.<br> | |
| − | + | ||
| − | [[ | + | *Zur Berechnung der Fehlerwahrscheinlichkeit gehen wir von der Annahme aus, dass $m_1$ gesendet wurde. Das bedeutet, dass die Entscheidung richtig ist, wenn der größte Detektionsausgangswert $y_1$ ist: |
| − | + | ::<math>{\rm Pr}({\cal{C}}) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr} \big [ (y_2 < y_1) \cap (y_3 < y_1) \cap ... \cap (y_{M} < y_1) | |
| − | + | \hspace{0.05cm}| \hspace{0.05cm} m = m_1\big ] = {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) | |
| + | \hspace{0.05cm}| \hspace{0.05cm}m = m_1\right ] | ||
| + | \hspace{0.01cm}.</math> | ||
| − | + | [[Datei:P ID2090 Dig T 4 5 S4b version1.png|right|frame|Nichtkohärente Empfängerstruktur für $M$–stufige FSK|class=fit]] | |
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ | ||
| + | * Die '''Fehlerwahrscheinlichkeit der M–stufigen FSK bei nichtkohärenter Demodulation''' ist gleich ${\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} })$. | ||
| + | |||
| + | *Nachfolgend wird gezeigt, dass ${\rm Pr}({\cal{C} })$ wie folgt dargestellt werden kann: | ||
| − | + | ::<math>{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } | |
| + | {(i+1) \cdot N_0}\right ] | ||
| + | \hspace{0.05cm}\hspace{0.5cm} \text{mit}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.</math> | ||
| − | [[ | + | *Im Sonderfall $M = 2$ ergibt sich natürlich wieder das im [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation|"letzten Abschnitt"]] erhaltene Ergebnis: |
| − | + | ::<math>p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} | |
| + | \hspace{0.05cm}.</math>}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Herleitung:}$ Das vorweg genommene Ergebnis soll nun in einigen Rechenschritten hergeleitet werden. | ||
| + | *Wir gehen von der Annahme aus, dass $m_1$ gesendet wurde. | ||
| + | |||
| + | *Das bedeutet, dass die Entscheidung richtig ist, wenn der größte Detektionsausgangswert $y_1$ ist. | ||
| + | |||
| + | *Ansonsten gibt es gewisse Analogien zur Herleitung der [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Fehlerwahrscheinlichkeit_bei_nichtkoh.C3.A4renter_2.E2.80.93FSK.E2.80.93Demodulation|"BFSK–Fehlerwahrscheinlichkeit"]].<br> | ||
| − | |||
| − | |||
| − | |||
| − | <b>(1)</b> Mit der bedingten Wahrscheinlichkeitsdichte | + | <b>(1)</b> Mit der bedingten Wahrscheinlichkeitsdichte $p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)$ erhält man: |
| − | :<math>{\rm Pr}({\cal{C}}) = \int_{0}^{\infty} {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) | + | ::<math>{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) |
| − | \hspace{0.05cm} | + | \hspace{0.05cm}\vert\hspace{0.05cm}y_1 = \eta_1, m = m_1\right ] \cdot p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1) \,\,{\rm d} \eta_1 |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(2)</b> Die Entscheidungswerte | + | <b>(2)</b> Die Entscheidungswerte $y_2$, $y_3$, ... , $y_M$ sind bei gegebenem $y_1$ statistisch unabhängig. Deshalb gilt: |
| − | :<math>{\rm Pr}({\cal{C}}) = \int_{0}^{\infty} \left \{ {\rm Pr} \ | + | ::<math>{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} \left \{ {\rm Pr} \big [ (y_2 < y_1) |
| − | \hspace{0.05cm} | + | \hspace{0.05cm}\vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \right \}^{M-1} \cdot p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1) \,\,{\rm d} \eta_1 |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(3)</b> Der ausgewählte Wert | + | <b>(3)</b> Der ausgewählte Wert $y_2$ konditioniert auf $m_1$ besitzt eine Rayleighverteilung mit Parameter $\sigma_n^2$: |
| − | :<math>{\rm Pr} \ | + | ::<math>{\rm Pr} \big [ (y_2 < y_1) |
| − | \hspace{0.05cm} | + | \hspace{0.05cm} \vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \int_{0}^{\eta_1} p_{y_2 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)\,\,{\rm d} \eta_2= 1 - {\rm exp } \big [ - {\eta_1^2 }/({2 \sigma_n^2})\big ] = 1 - a \hspace{0.2cm}{\rm(Abk\ddot{u}rzung)} |
| − | |||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(4)</b> Gesucht ist nun der Ausdruck (1 & | + | <b>(4)</b> Gesucht ist nun der Ausdruck $(1 -a)^{M-1}$, für den mit der Abkürzung aus <b>(3)</b> gilt: |
| − | :<math> (1-a)^{M-1} \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot (-1)^i \cdot a^i = | + | ::<math> (1-a)^{M-1} \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot (-1)^i \cdot a^i = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] |
| − | |||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(5)</b> | + | <b>(5)</b> $y_1$ besitzt konditioniert auf $m=m_1$ eine [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Rayleigh.E2.80.93_und_Riceverteilung|Riceverteilung]]. Die Wahrscheinlichkeit für eine korrekte Entscheidung lässt sich somit in folgende Form bringen: |
| − | :<math>{\rm Pr}({\cal{C}}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot | + | ::<math>{\rm Pr}({\cal{C} }) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \int_{0}^{\infty} {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \cdot \frac{\eta_1}{ \sigma_n^2}\cdot |
| − | + | {\rm exp } \left [ - \frac{\eta_1^2 + E_{\rm S} }{2 \sigma_n^2}\right ] \cdot {\rm I }_0 | |
| − | {\rm exp } \left [ - \frac{\eta_1^2 + E_{\rm S}}{2 \sigma_n^2}\right ] \cdot {\rm I }_0 | + | \left [ \frac{\eta_1 \cdot \sqrt{E_{\rm S} } }{ \sigma_n^2}\right ] \,\,{\rm d} \eta_1 |
| − | \left [ \frac{\eta_1 \cdot \sqrt{E_{\rm S}}}{ \sigma_n^2}\right ] \,\,{\rm d} \eta_1 | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | <b>(6)</b> Durch Substitutionen gelingt es, den Integranden | + | <b>(6)</b> Durch Substitutionen gelingt es, den Integranden gemäß der Riceverteilung zu gestalten. Da sich jede Wahrscheinlichkeitsdichte zu Eins integriert, erhält man: |
| − | :<math>{\rm Pr}({\cal{C}}) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } | + | ::<math>{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } |
{(i+1) \cdot N_0}\right ] | {(i+1) \cdot N_0}\right ] | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}\hspace{0.5cm} \text{mit}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.</math> |
| − | <b>(7)</b> Der Sonderfall | + | <b>(7)</b> Der Sonderfall $M = 2$ führt zum genau gleichen Ergebnis, wie für die binäre FSK berechnet: |
| − | :<math>{\rm Pr}({\cal{C}}) | + | ::<math>{\rm Pr}({\cal{C} }) = (-1)^0 \cdot {2-1 \choose 0 } \cdot \frac{1}{0+1} \cdot {\rm exp } \left [ - \frac{0 \cdot E_{\rm S} } |
| − | {(i+1) \cdot N_0}\right ] + | + | {(i+1) \cdot N_0}\right ] + (-1)^1 \cdot {2-1 \choose 1 } \cdot \frac{1}{1+1} \cdot {\rm exp } \left [ - \frac{1 \cdot E_{\rm S} } |
| − | + | {(i+1) \cdot N_0}\right ] </math> | |
| − | {(i+1) \cdot N_0}\right ] | + | ::<math> \Rightarrow \hspace{0.5cm} {\rm Pr}({\cal{C} }) = 1 - {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)} |
| − | + | \hspace{0.5cm} \Rightarrow \hspace{0.5cm} {\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} }) = {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)} | |
| − | \hspace{ | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | <div align="right">$\text{q.e.d.}$</div>}} | ||
| − | == Aufgaben == | + | == Aufgaben zum Kapitel== |
<br> | <br> | ||
| − | [[Aufgaben:4. | + | [[Aufgaben:4.17_Nichtkohärentes_On-Off-Keying|Aufgabe 4.17: Nichtkohärentes On-Off-Keying]] |
| − | [[ | + | [[Aufgaben:4.17Z_Rayleigh-_und_Riceverteilung|Aufgabe 4.17Z: Rayleigh- und Riceverteilung]] |
| − | [[Aufgaben:4. | + | [[Aufgaben:4.18_Nichtkohärente_FSK–Demodulation|Aufgabe 4.18: Nichtkohärente FSK–Demodulation]] |
| − | [[ | + | [[Aufgaben:4.18Z_BER_von_kohärenter_und_nichtkohärenter_FSK|Aufgabe 4.18Z: BER von kohärenter und nichtkohärenter FSK]] |
| − | [[Aufgaben:4. | + | [[Aufgaben:4.19_Orthogonale_mehrstufige_FSK|Aufgabe 4.19: Orthogonale mehrstufige FSK]] |
{{Display}} | {{Display}} | ||
Aktuelle Version vom 12. Oktober 2022, 12:48 Uhr
Inhaltsverzeichnis
Rayleigh– und Riceverteilung
Die für eine kohärente Demodulation erforderliche Schätzung des Phasenwinkels aus dem ankommenden Signal ist bei vielen Anwendungen nicht oder nur eingeschränkt möglich. So führt die Bewegung eines Mobilteilnehmers mit hoher Geschwindigkeit zu sehr schnellen zeitlichen Änderungen des Phasenwinkels $\phi$, was dessen ausreichend genaue Bestimmung erschwert oder gar verhindert.
Diese Tatsache führt zu den nichtkohärenten Demodulationsverfahren mit dem Vorteil reduzierter Komplexität, allerdings mit erhöhter Verfälschungswahrscheinlichkeit. Bei der Herleitung der Gleichungen stößt man auf zwei Wahrscheinlichkeitsdichtefunktionen, die hier vorneweg angegeben werden:
- Die Rayleighverteilung erhält man für die WDF der Zufallsgröße $y$ mit Realisierung $\eta$, die sich aus den beiden gaußverteilten und statistisch unabhängigen Komponenten $u$ und $v$ $($beide mit der gleichen Streuung $\sigma_n)$ wie folgt ergibt:
- \[y = \sqrt{u^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) ={\eta}/{\sigma_n^2} \cdot {\rm exp } \left [ - {\eta^2}/{ (2\sigma_n^2)}\right ] \hspace{0.05cm}.\]
- Die Riceverteilung erhält man unter gleichen Randbedingungen für den Fall, dass bei einer der Komponenten $(u$ oder $v)$ noch eine Konstante $C$ addiert wird:
- \[y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = {\eta}/{\sigma_n^2} \cdot {\rm exp } \left [ - ({\eta^2 + C^2})/(2 \sigma_n^2) \right ] \cdot {\rm I }_0 \left [{\eta \cdot C}/{ \sigma_n^2}\right ] \hspace{0.05cm}.\]
- Die Riceverteilung verwendet die "modifizierte Besselfunktion nullter Ordnung", deren Definition und Reihenentwicklung wie folgt lauten:
- \[{\rm I }_0 (x) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{-x \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} \approx \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(x/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
Die Grafik zeigt die Wahrscheinlichkeitsdichtefunktionen von Rayleigh– und Riceverteilung. Zu dieser Darstellung ist anzumerken:
- Die Riceverteilung ist durch die beiden Parameter $C$ und $\sigma_n$ bestimmt. Mit $C = 0$ ist die Rice–WDF identisch mit der Rayleigh–WDF.
- Die Rayleigh–WDF mit größerem $\sigma_n$ ist formgleich wie für $\sigma_n = 0.5$ dargestellt, aber im Verhältnis der Streuungen breiter und niedriger.
- $\sigma_n$ gibt die Streuung der beiden gaußverteilten Zufallsgrößen $u$ und $v$ an und nicht die Streuung der rayleighverteilten Zufallsgröße $y$. Diese ist:
- \[\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n \hspace{0.05cm}.\]
- Die Rayleighverteilung ist extrem unsymmetrisch, erkennbar am großen Wert für das "Zentralmoment 3. Ordnung" ⇒ "Charliersche Schiefe":
- $$\mu_3/\sigma_y \approx 0.27.$$
- Die Riceverteilung ist um so symmetrischer, je größer das Verhältnis von Mittelwert und Streuung $(C/\sigma_n)$ ist. Für $C/\sigma_n \ge 4$ ist $\mu_3 \approx 0$.
- Je größer $C/\sigma_n$ ist, um so mehr nähert sich die Riceverteilung $($mit $C$, $\sigma_n)$ einer Gaußverteilung mit Mittelwert $C$ und Streuung $\sigma_n$ an:
- $$p_y (\eta) \approx \frac{1}{\sqrt{2\pi} \cdot \sigma_n} \cdot {\rm exp } \left [ - \frac{(\eta - C)^2}{2 \sigma_n^2}\right ]$$
- $$ \Rightarrow \hspace{0.3cm} m_y = C\hspace{0.05cm},\hspace{0.2cm}\sigma_y = \sigma_n \hspace{0.05cm}.$$
Nichtkohärente Demodulation von On–Off–Keying
Wir betrachten "On–Off–Keying" $\rm (OOK)$ bzw. $\rm 2–ASK)$ im äquivalenten Tiefpassbereich.
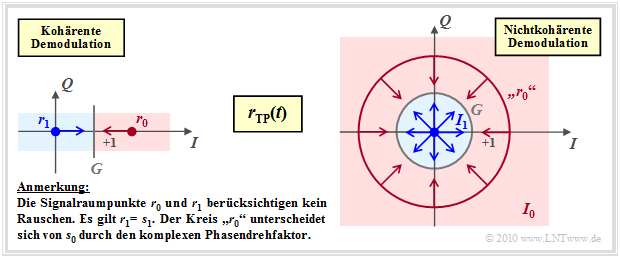
- Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals $\boldsymbol{r}(t)$ gleich der des Sendesignals $\boldsymbol{s}(t)$ und besteht aus zwei Punkten (linke Grafik).
- Die Entscheidungsgrenze $G$ liegt in der Mitte zwischen diesen Punkten $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$. Die Pfeile markieren die grobe Richtung von Rauschvektoren, die eventuell zu Übertragungsfehlern führen.
Dagegen gilt bei nichtkohärenter Demodulation (rechte Grafik):
- Der Punkt $\boldsymbol{r}_1 = \boldsymbol{s}_1 = 0$ bleibt weiter erhalten. Dagegen kann $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ auf jeden Punkt des Kreises um $\boldsymbol{s}_0$ liegen, da $\phi$ unbekannt ist.
- Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun zweidimensional zu interpretieren, wie durch die Pfeile in der rechten Grafik angedeutet.
- Das Entscheidungsgebiet $I_1$ ist ein Kreis, dessen Radius $G$ ein optimierbarer Parameter ist. Das Entscheidungsgebiet $I_0$ liegt außerhalb des Kreises.
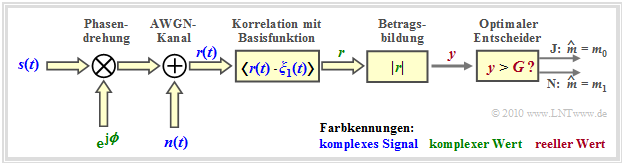
Damit liegt die Strukur des optimalen OOK–Empfängers (im äquivalenten Tiefpassbereich) fest. Entsprechend dieser zweiten Grafik gilt:
- Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ ist aufgrund des Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex.
- Erforderlich ist demzufolge nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}_1(t)$.
- Das Ergebnis ist der (komplexe) Detektorausgangswert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.
- Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$.
- Die Fehlerwahrscheinlichkeit ist bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}(\boldsymbol{m}_0) = {\rm Pr}(\boldsymbol{m}_1) =1/2$ :
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}|\hspace{0.05cm} m_0) \,{\rm d} \eta + {1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} m_1) \,{\rm d} \eta \hspace{0.05cm}.\]
- Aufgrund der Rice –WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_0)$ und der Rayleigh–WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_1)$ kann allerdings diese Wahrscheinlichkeit nur numerisch ermittelt werden.
- Die optimale Entscheidungsgrenze $G$ ist vorher als die Lösung der folgenden Gleichung zu bestimmen:
- \[p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_0) = p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_1) \hspace{0.05cm}.\]
$\text{Beispiel 1:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_n = 0.5$ und $C = 2$, wobei die (rote) Rice–WDF durch eine Gauß–WDF mit Mittelwert $C$ und Streuung $\sigma_n$ approximiert ist.
Man erkennt daraus:
- Die optimale Entscheidungsgrenze $($hier: $G \approx 1.25)$ ergibt sich aus dem Schnittpunkt der beiden Kurven.
- Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen.
- Im Beispiel ergibt sich $p_{\rm S} \approx 5\%$.
⇒ Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem HTML5/JavaScript–Berechnungstool "Nichtkohärentes On–Off–Keying" bestimmen.
Nichtkohärente Demodulation von binärer FSK (2–FSK)
Wie schon im "letzten Kapitel" gezeigt wurde, lässt sich "Binary Frequency Shift Keying" $\rm (2–FSK)$ im äquivalenten Tiefpassbereich durch die Basisfunktionen
- \[\xi_1(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},\]
- \[ \xi_2(t) = \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}\]
darstellen. Um Orthogonalität zwischen diesen beiden komplexen Basisfunktionen zu erreichen, muss der "Modulationsindex" $h$ ganzzahlig gewählt werden:
- \[< \hspace{-0.05cm}\xi_1(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} h = 2 \cdot \Delta f_{\rm A} \cdot T\hspace{0.05cm}= 1, 2, 3, \text{...}\]
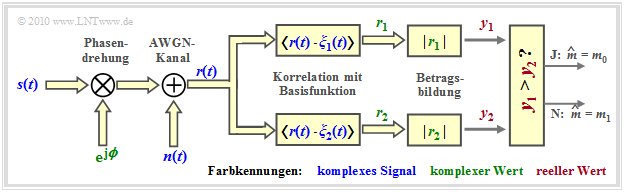
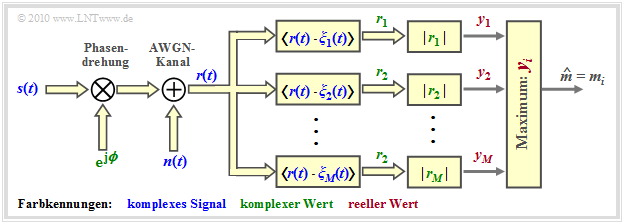
Die Grafik zeigt die Struktur zur nichtkohärenten orthogonalen Demodulation der binären FSK.
Im rauschfreien Fall ⇒ $n(t) \equiv 0$ gilt für die Ausgänge der beiden Korrelatoren:
- \[r_1 = \hspace{0.2cm} < \hspace{-0.05cm}r(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_1(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0\hspace{0.05cm}, \hspace{0.2cm} {\rm falls}\hspace{0.25cm} m = m_1\hspace{0.05cm},\]
- \[ r_2 = \hspace{0.2cm} < \hspace{-0.05cm}r(t) \hspace{0.1cm} \cdot \hspace{0.1cm} \xi_2(t) \hspace{-0.05cm}> \hspace{0.2cm}= 0\hspace{0.05cm}, \hspace{0.2cm} {\rm falls}\hspace{0.25cm} m = m_0\hspace{0.05cm}.\]
Nach jeweiliger Betragsbildung ⇒ $y_1 = |r_1|, \ \ y_2 = |r_2|$ ist dann folgende Entscheidungsregel anwendbar:
- \[\hat{m} = \left\{ \begin{array}{c} m_0 \\ m_1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm} y_1 > y_2 \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} y_1 < y_2 \hspace{0.05cm}.\\ \end{array}\]
Zur einfacheren Entscheiderrealisierung kann auch die Differenz $y_1 - y_2$ mit der Entscheidungsgrenze $G = 0$ ausgewertet werden.
Fehlerwahrscheinlichkeit bei nichtkohärenter 2–FSK–Demodulation
Im Folgenden wird die Fehlerwahrscheinlichkeit unter der Annahme berechnet, dass $m = m_0$ gesendet wurde.
- Unter der weiteren Voraussetzung gleichwahrscheinlicher binärer Nachrichten $m_0$ und $m_1$ ist die absolute Fehlerwahrscheinlichkeit genau so groß:
- $${\rm Pr}({\cal{E}}) = {\rm Pr}({\cal{E}}\hspace{0.05cm} | \hspace{0.05cm}m_0) \hspace{0.05cm}.$$
- Mit $m = m_0$ ergeben sich für die komplexen Korrelationsausgangswerte $r_i$ und deren Beträge $y_i$:
- \[r_1 = \sqrt{E} \cdot {\rm e}^{{\rm j}\phi} + n_1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_1 = |r_1|\hspace{0.15cm}{\rm ist}\hspace{0.15cm}{\rm riceverteilt} \hspace{0.05cm},\]
- \[ r_2 = n_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_2 = |r_2|\hspace{0.15cm}{\rm ist}\hspace{0.15cm}{\rm rayleighverteilt} \hspace{0.05cm}.\]
- Hierbei steht $E$ wegen $M = 2$ für die "mittlere Symbolenergie" $(E_{\rm S})$ und diedie "mittlere Bitenergie" $(E_{\rm B})$ gleichermaßen. $n_1$ und $n_2$ sind unkorrelierte komplexe Rauschgrößen mit Mittelwert Null und Varianz $2 \cdot \sigma_n^2$. Somit lautet die "Verbundwahrscheinlichkeitsdichtefunktion":
- \[p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) =
p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot
p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0)
\hspace{0.05cm},\]
- $$p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E}}/{ \sigma_n^2}\right ] \hspace{0.05cm},$$
- $$ p_{y_2 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$
- Die Fehlerwahrscheinlichkeit ergibt sich allgemein wie folgt:
- \[{\rm Pr}({\cal{E}}) = \int_{0}^{\infty} \int_{\eta_1}^{\infty} p_{y_1,\hspace{0.03cm} y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_1, \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0) \,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm}| \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}| \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}| \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}| \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
$\text{Fazit:}$ Für die Fehlerwahrscheinlichkeit bei nichtkohärenter Demodulation der binären FSK erhält man nach einigen mathematischen Umformungen das überraschend einfache Ergebnis
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} \hspace{0.05cm}.\]
- Zum Vergleich sei nochmals das Ergebnis für die kohärente Demodulation angegeben:
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {\rm Q}(\sqrt{ E_{\rm S}/N_0}) \hspace{0.05cm}.\]
$\text{Herleitung:}$ Das vorweg genommene Ergebnis soll nun in einigen Rechenschritten hergeleitet werden. Wir gehen dabei von den folgenden Gleichungen aus:
- $${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_0) \cdot \int_{\eta_1}^{\infty}
p_{y_2 \hspace{0.03cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2\,\,{\rm d} \eta_1
\hspace{0.05cm},\hspace{0.5cm}\text{mit}$$
- $$p_{y_1 \hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [{\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ] \hspace{0.05cm},$$
- $$p_{y_\hspace{0.01cm}\vert \hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0) = {\eta_2}/{\sigma_n^2} \cdot {\rm e }^{ - \eta_2^2 /({2 \sigma_n^2}) } \hspace{0.05cm}.$$
(1) Das innere Integral gibt die Wahrscheinlichkeit an, dass die rayleighverteilte Zufallsgröße $\eta_2$ größer ist als $\eta_1$ – siehe Musterlösung zur "Aufgabe 4.17Z":
- $$\int_{\eta_1}^{\infty} p_{y_2 \hspace{0.03cm}\vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm}\vert \hspace{0.05cm}m_0)\,\,{\rm d} \eta_2 = {\rm e }^{ - \eta_1^2 /({2 \sigma_n^2}) } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}({\cal{E} }) = \int_{0}^{\infty}{\eta_1}/{\sigma_n^2} \cdot {\rm e }^{ - ({2\eta_1^2 + E})/({2 \sigma_n^2}) }\cdot {\rm I }_0 \left [ {\eta_1 \cdot \sqrt{E} }/{ \sigma_n^2}\right ]\,\,{\rm d} \eta_1 \hspace{0.05cm}.$$
(2) Mit den (willkürlichen) Substitutionen $C_0^2 = E/4$ und $\sigma_0^2 = \sigma_n^2/2$, erhält man:
- $${\rm Pr}({\cal{E} }) = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} \cdot {\rm exp } \left [ - \frac{2 \eta_1^2 + 4 C_0^2}{4 \sigma_0^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot 2C_0}{ 2 \sigma_0^2}\right ]\,\,{\rm d} \eta_1 = \int_{0}^{\infty} \frac{\eta_1}{2 \cdot \sigma_0^2} \cdot {\rm exp } \left [ - \frac{\eta_1^2 + 2 C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 \hspace{0.05cm}.$$
(3) Durch Verschieben von Anteilen vor das Integral gelingt es, dass der Integrand wieder eine Riceverteilung beschreibt:
- \[{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] \cdot \int\limits_{0}^{\infty} \frac{\eta_1}{ \sigma_0^2} \cdot {\rm exp } \left [ - \frac{\eta_1^2 + C_0^2}{2 \sigma_0^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot C_0}{ \sigma_0^2}\right ]\,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(4) Der Integrand beschreibt nun die Rice–WDF. Das Integral über das gesamte Definitionsgebiet von $0$ bis $+\infty$ ergibt wie bei jeder WDF den Wert Eins, so dass gilt:
- \[{\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ]\hspace{0.05cm}.\]
(5) Mit $C_0^2 = E/4$ und $\sigma_0^2 = \sigma_n^2/2$ sowie der allgemein gültigen Beziehung $\sigma_n^2 = N_0$ erhält man schließlich:
- $${\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm exp } \left [ - \frac{ C_0^2}{2 \sigma_0^2}\right ] = {1}/{2} \cdot {\rm exp } \left [ - \frac{ E_{\rm S}/4}{N_{\rm 0}/2}\right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)}\hspace{0.05cm}.$$
$E_{\rm S}$ gibt hierbei die mittlere Signalenergie pro Symbol an, die bei FSK gleich der Normierungsenergie $E$ ist.
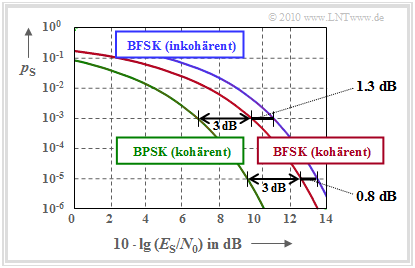
$\text{Beispiel 2:}$ Die Grafik stellt die Fehlerwahrscheinlichkeitskurven beider Demodulationsverfahren in Abhängigkeit des AWGN–Qotienten $E_{\rm S}/N_0$ vergleichend gegenüber.
Man erkennt:
- Die nichtkohärente BFSK (rote Kurve) benötigt gegenüber der kohärenten BFSK (blaue Kurve) bei $p_{\rm S}= 10^{-5}$ ein um $0.8 \ \rm dB$ größeres $E_{\rm S}/N_0$.
- Bei $p_{\rm S}= 10^{-3}$ beträgt der Abstand sogar $1.3 \ \rm dB$.
- Dagegen beträgt der Abstand zwischen der kohärenten binären FSK von der kohärenten BPSK unabhängig von der Fehlerwahrscheinlichkeit stets $1.3 \ \rm dB$.
Nichtkohärente Demodulation von mehrstufiger FSK
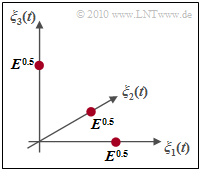
Wir betrachten nun die Nachrichtenmenge $\{m_1, m_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, m_{M}\}$ und bezeichnen $M$ als Stufenzahl.
- Voraussetzung für die Anwendung des Modulationsverfahrens "Frequency Shift Keying" und zugleich eines nichtkohärenten Demodulators ist wie bei der binären FSK ein ganzzahliger Modulationsindex $h$.
- In diesem Fall ist die $M$–stufige FSK orthogonal und es ergibt sich eine Signalraumkonstellation, wie in der nebenstehenden Grafik für den Sonderfall $M = 3$ dargestellt.
Der nichtkohärente Demodulator ist nachfolgend skizziert.
- Gegenüber der "Empfängerstruktur für binäre FSK" unterscheidet sich dieser Empfänger lediglich durch $M$ Zweige anstelle von nur zweien, welche die Vergleichswerte $y_1$, $y_2$, ... , $y_M$ liefern.
- Zur Berechnung der Fehlerwahrscheinlichkeit gehen wir von der Annahme aus, dass $m_1$ gesendet wurde. Das bedeutet, dass die Entscheidung richtig ist, wenn der größte Detektionsausgangswert $y_1$ ist:
- \[{\rm Pr}({\cal{C}}) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr} \big [ (y_2 < y_1) \cap (y_3 < y_1) \cap ... \cap (y_{M} < y_1) \hspace{0.05cm}| \hspace{0.05cm} m = m_1\big ] = {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) \hspace{0.05cm}| \hspace{0.05cm}m = m_1\right ] \hspace{0.01cm}.\]
$\text{Fazit:}$
- Die Fehlerwahrscheinlichkeit der M–stufigen FSK bei nichtkohärenter Demodulation ist gleich ${\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} })$.
- Nachfolgend wird gezeigt, dass ${\rm Pr}({\cal{C} })$ wie folgt dargestellt werden kann:
- \[{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] \hspace{0.05cm}\hspace{0.5cm} \text{mit}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.\]
- Im Sonderfall $M = 2$ ergibt sich natürlich wieder das im "letzten Abschnitt" erhaltene Ergebnis:
- \[p_{\rm S} = {\rm Pr}({\cal{E} }) = {1}/{2} \cdot {\rm e}^{-E_{\rm S}/(2 N_0)} \hspace{0.05cm}.\]
$\text{Herleitung:}$ Das vorweg genommene Ergebnis soll nun in einigen Rechenschritten hergeleitet werden.
- Wir gehen von der Annahme aus, dass $m_1$ gesendet wurde.
- Das bedeutet, dass die Entscheidung richtig ist, wenn der größte Detektionsausgangswert $y_1$ ist.
- Ansonsten gibt es gewisse Analogien zur Herleitung der "BFSK–Fehlerwahrscheinlichkeit".
(1) Mit der bedingten Wahrscheinlichkeitsdichte $p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)$ erhält man:
- \[{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} {\rm Pr} \left [ \hspace{0.1cm} \bigcap\limits_{k = 2}^M (y_k < y_1) \hspace{0.05cm}\vert\hspace{0.05cm}y_1 = \eta_1, m = m_1\right ] \cdot p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1) \,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(2) Die Entscheidungswerte $y_2$, $y_3$, ... , $y_M$ sind bei gegebenem $y_1$ statistisch unabhängig. Deshalb gilt:
- \[{\rm Pr}({\cal{C} }) = \int_{0}^{\infty} \left \{ {\rm Pr} \big [ (y_2 < y_1) \hspace{0.05cm}\vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \right \}^{M-1} \cdot p_{y_1 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_1 \hspace{0.05cm} \vert \hspace{0.05cm}m_1) \,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(3) Der ausgewählte Wert $y_2$ konditioniert auf $m_1$ besitzt eine Rayleighverteilung mit Parameter $\sigma_n^2$:
- \[{\rm Pr} \big [ (y_2 < y_1) \hspace{0.05cm} \vert \hspace{0.05cm}y_1 = \eta_1, m = m_1\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \int_{0}^{\eta_1} p_{y_2 \hspace{0.01cm} \vert\hspace{0.03cm}m} ( \eta_2 \hspace{0.05cm} \vert \hspace{0.05cm}m_1)\,\,{\rm d} \eta_2= 1 - {\rm exp } \big [ - {\eta_1^2 }/({2 \sigma_n^2})\big ] = 1 - a \hspace{0.2cm}{\rm(Abk\ddot{u}rzung)} \hspace{0.05cm}.\]
(4) Gesucht ist nun der Ausdruck $(1 -a)^{M-1}$, für den mit der Abkürzung aus (3) gilt:
- \[ (1-a)^{M-1} \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot (-1)^i \cdot a^i = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \hspace{0.05cm}.\]
(5) $y_1$ besitzt konditioniert auf $m=m_1$ eine Riceverteilung. Die Wahrscheinlichkeit für eine korrekte Entscheidung lässt sich somit in folgende Form bringen:
- \[{\rm Pr}({\cal{C} }) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \int_{0}^{\infty} {\rm exp } \left [ - \frac{i \cdot \eta_1^2 }{2 \sigma_n^2}\right ] \cdot \frac{\eta_1}{ \sigma_n^2}\cdot {\rm exp } \left [ - \frac{\eta_1^2 + E_{\rm S} }{2 \sigma_n^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta_1 \cdot \sqrt{E_{\rm S} } }{ \sigma_n^2}\right ] \,\,{\rm d} \eta_1 \hspace{0.05cm}.\]
(6) Durch Substitutionen gelingt es, den Integranden gemäß der Riceverteilung zu gestalten. Da sich jede Wahrscheinlichkeitsdichte zu Eins integriert, erhält man:
- \[{\rm Pr}({\cal{C} }) = \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] \hspace{0.05cm}\hspace{0.5cm} \text{mit}\hspace{0.5cm} E_{\rm S} = E_{\rm B} \cdot {\rm log_2}(M)\hspace{0.05cm}.\]
(7) Der Sonderfall $M = 2$ führt zum genau gleichen Ergebnis, wie für die binäre FSK berechnet:
- \[{\rm Pr}({\cal{C} }) = (-1)^0 \cdot {2-1 \choose 0 } \cdot \frac{1}{0+1} \cdot {\rm exp } \left [ - \frac{0 \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] + (-1)^1 \cdot {2-1 \choose 1 } \cdot \frac{1}{1+1} \cdot {\rm exp } \left [ - \frac{1 \cdot E_{\rm S} } {(i+1) \cdot N_0}\right ] \]
- \[ \Rightarrow \hspace{0.5cm} {\rm Pr}({\cal{C} }) = 1 - {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} {\rm Pr}({\cal{E} }) = 1 - {\rm Pr}({\cal{C} }) = {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)} \hspace{0.05cm}.\]
Aufgaben zum Kapitel
Aufgabe 4.17: Nichtkohärentes On-Off-Keying
Aufgabe 4.17Z: Rayleigh- und Riceverteilung
Aufgabe 4.18: Nichtkohärente FSK–Demodulation
Aufgabe 4.18Z: BER von kohärenter und nichtkohärenter FSK
Aufgabe 4.19: Orthogonale mehrstufige FSK