Modulationsverfahren/Quadratur–Amplitudenmodulation: Unterschied zwischen den Versionen
| Zeile 175: | Zeile 175: | ||
*Aus den eingezeichneten Entscheidungsgebieten erkennt man, dass hier die Detektion nicht auf zwei Binärentscheidungen zurückgeführt werden kann. | *Aus den eingezeichneten Entscheidungsgebieten erkennt man, dass hier die Detektion nicht auf zwei Binärentscheidungen zurückgeführt werden kann. | ||
*Auch die 4–QAM (links) kann als vierstufige Phasenmodulation aufgefasst werden $($Phasenlagen $±45^\circ$, $±135^\circ)$. | *Auch die 4–QAM (links) kann als vierstufige Phasenmodulation aufgefasst werden $($Phasenlagen $±45^\circ$, $±135^\circ)$. | ||
| − | *Gegenüber der QPSK ergibt sich eine Drehung um $±45^\circ$ $(π/4)$ | + | *Gegenüber der QPSK ergibt sich eine Drehung um $±45^\circ$ $(π/4)$ ⇒ die 4–QAM oft auch als ${\rm π/4}\text{–QPSK}$ bezeichnet. |
| − | *Ähnlich wie man bei der BPSK durch Vorcodierung zur DPSK kommt, kann auch die 4–PSK zur 4–DPSK erweitert und dadurch die Demodulation erleichtert werden. Diese wurde zum Beispiel bei der Datenübertragung über Telefonkanäle gemäß | + | *Ähnlich wie man bei der BPSK durch Vorcodierung zur DPSK kommt, kann auch die 4–PSK zur 4–DPSK erweitert und dadurch die Demodulation erleichtert werden. |
| + | *Diese wurde zum Beispiel bei der Datenübertragung über Telefonkanäle gemäß CCITT–Empfehlung „V26” angewendet $($Trägerfrequenz $\text{1800 Hz}$, Datenrate $\text{2400 bit/s)}$. | ||
Die beiden rechten Diagramme zeigen höherstufige Modulationsverfahren: | Die beiden rechten Diagramme zeigen höherstufige Modulationsverfahren: | ||
| − | *Die 8–PSK (bzw. 8–DPSK | + | *Die 8–PSK (bzw. 8–DPSK) erlaubt entsprechend der CCITT–Empfehlung „V27” beim Telefonkanal eine Datenrate von bis zu $\text{4800 bit/s}$. |
| − | *Die Empfehlung „V29” sieht mit der 16–ASK/PSK eine hybride Modulationsform vor, die bei | + | *Die Empfehlung „V29” sieht mit der 16–ASK/PSK eine hybride Modulationsform vor, die bei fest verschalteten Leitungen Datenraten bis $\text{9600 bit/s}$ ermöglicht. |
==Nyquist– und Wurzel–Nyquist–QAM–Systeme== | ==Nyquist– und Wurzel–Nyquist–QAM–Systeme== | ||
<br> | <br> | ||
| − | Bisher wurde in diesem Kapitel aus Darstellungsgründen stets vom rechteckförmigen Sendegrundimpuls ausgegangen. In der Praxis verwendet man aber meist eine ''Wurzel–Nyquist–Charakteristik'' entsprechend der [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme#Wurzel.E2.80.93Nyquist.E2.80.93Systeme|Beschreibung]] im Buch „Digitalsignalübertragung”. In aller Kürze lassen sich diese Systeme wie folgt charakterisieren: | + | Bisher wurde in diesem Kapitel aus Darstellungsgründen stets vom rechteckförmigen Sendegrundimpuls ausgegangen. In der Praxis verwendet man aber meist eine '''Wurzel–Nyquist–Charakteristik''' entsprechend der [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme#Wurzel.E2.80.93Nyquist.E2.80.93Systeme|Beschreibung]] im Buch „Digitalsignalübertragung”. In aller Kürze lassen sich diese Systeme wie folgt charakterisieren: |
| − | *Der Empfängerfrequenzgang $H_{\rm E}(f)$ wird hier formgleich mit dem (normierten) Sendeimpulsspektrum $H_{\rm S}(f)$ gewählt, was unter der Nebenbedingung der Leistungsbegrenzung (das heißt: bei konstanter mittlerer Sendeleistung) zur | + | *Der Empfängerfrequenzgang $H_{\rm E}(f)$ wird hier formgleich mit dem (normierten) Sendeimpulsspektrum $H_{\rm S}(f)$ gewählt, was unter der Nebenbedingung der Leistungsbegrenzung (das heißt: bei konstanter mittlerer Sendeleistung) zur kleinstmöglichen Fehlerwahrscheinlichkeit führt. |
| − | *Der Gesamtfrequenzgang $H_{\rm Nyq}(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt das [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#1.2FT.E2.80.93Nyquistspektren_.281.29|erste Nyquistkriterium]], so dass es beim Empfänger zu keinen Impulsinterferenzen kommt. $H_{\rm S}(f)$ und $H_{\rm E}(f)$ haben somit jeweils eine Wurzel–Nyquist–Charakteristik. | + | *Der Gesamtfrequenzgang $H_{\rm Nyq}(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt das [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#1.2FT.E2.80.93Nyquistspektren_.281.29|erste Nyquistkriterium]], so dass es beim Empfänger zu keinen Impulsinterferenzen kommt. $H_{\rm S}(f)$ und $H_{\rm E}(f)$ haben somit jeweils eine Wurzel–Nyquist–Charakteristik. |
| − | *Für den Frequenzgang $H_{\rm Nyq}(f)$ verwendet man einen [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Cosinus-Rolloff-Tiefpass|Cosinus–Rolloff–Tiefpass]] $H_{\rm CRO}(f)$ mit der äquivalenten Bandbreite $Δf_{\rm CRO} = 1/T$ und frei wählbarem Rolloff–Faktor $(0 ≤ r ≤ 1)$. Das interaktive Applet [[Applets:Frequenzgang_und_Impulsantwort|Frequenzgang und Impulsantwort]] verdeutlicht den Frequenzgang und die Impulsantwort dieses Tiefpasses. | + | *Für den Frequenzgang $H_{\rm Nyq}(f)$ verwendet man einen [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Cosinus-Rolloff-Tiefpass|Cosinus–Rolloff–Tiefpass]] $H_{\rm CRO}(f)$ mit der äquivalenten Bandbreite $Δf_{\rm CRO} = 1/T$ und frei wählbarem Rolloff–Faktor $(0 ≤ r ≤ 1)$. Das interaktive Applet [[Applets:Frequenzgang_und_Impulsantwort|Frequenzgang und Impulsantwort]] verdeutlicht den Frequenzgang und die Impulsantwort dieses Tiefpasses. |
*Der Vorteil dieser Wurzel–Nyquist–Systeme ist die deutlich kleinere Bandbreite $(1 + r)/T$ gegenüber der bisher betrachteten Konfiguration mit rechteckförmigem $g_s(t)$ und rechteckförmigem $h_{\rm E}(t)$, dessen Spektrum (theoretisch) unendlich weit ausgedehnt ist. | *Der Vorteil dieser Wurzel–Nyquist–Systeme ist die deutlich kleinere Bandbreite $(1 + r)/T$ gegenüber der bisher betrachteten Konfiguration mit rechteckförmigem $g_s(t)$ und rechteckförmigem $h_{\rm E}(t)$, dessen Spektrum (theoretisch) unendlich weit ausgedehnt ist. | ||
*Hinsichtlich Fehlerwahrscheinlichkeit ändert sich gegenüber der Rechteck–Rechteck–Konfiguration nichts, da der Grundimpuls $g_d(t)$ vor dem Entscheider äquidistante Nulldurchgänge aufweist und somit Impulsinterferenzen vermieden werden. | *Hinsichtlich Fehlerwahrscheinlichkeit ändert sich gegenüber der Rechteck–Rechteck–Konfiguration nichts, da der Grundimpuls $g_d(t)$ vor dem Entscheider äquidistante Nulldurchgänge aufweist und somit Impulsinterferenzen vermieden werden. | ||
| − | [[Datei:Mod_T_4_3_S8_vers2.png| | + | [[Datei:Mod_T_4_3_S8_vers2.png|right|frame|Phasendiagramme der 4-QAM bei Wurzel-Nyquist-Konfiguration]] |
Die Grafik zeigt die Phasendiagramme für diesen Fall, die dem Buch [Kam04]<ref name="Kam04">Kammeyer, K.D.: ''Nachrichtenübertragung.'' Stuttgart: B.G. Teubner, 4. Auflage, 2004.</ref> entnommen sind. Der Rolloff–Faktor beträgt $r = 0.5$. Man erkennt aus diesen Darstellungen: | Die Grafik zeigt die Phasendiagramme für diesen Fall, die dem Buch [Kam04]<ref name="Kam04">Kammeyer, K.D.: ''Nachrichtenübertragung.'' Stuttgart: B.G. Teubner, 4. Auflage, 2004.</ref> entnommen sind. Der Rolloff–Faktor beträgt $r = 0.5$. Man erkennt aus diesen Darstellungen: | ||
Version vom 21. April 2020, 15:30 Uhr
Inhaltsverzeichnis
- 1 Allgemeine Beschreibung und Signalraumzuordnung
- 2 Systembeschreibung durch das äquivalente Tiefpass–Signal
- 3 Leistung und Energie von QAM–Signalen
- 4 Signalverläufe der 4–QAM
- 5 Fehlerwahrscheinlichkeit der 4–QAM
- 6 Quadratische QAM–Signalraumkonstellationen
- 7 Weitere Signalraumkonstellationen
- 8 Nyquist– und Wurzel–Nyquist–QAM–Systeme
- 9 Offset–Quadraturamplitudenmodulation
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Allgemeine Beschreibung und Signalraumzuordnung
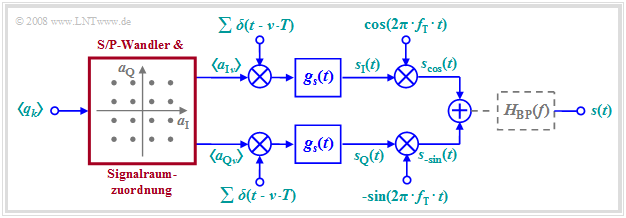
Aufgrund der Orthogonalität von Cosinus und (Minus–)Sinus kann man über einen Übertragungskanal zwei Datenströme unabhängig voneinander übertragen. Die Grafik zeigt das allgemeine Blockschaltbild.
Dieses sehr allgemeine Modell lässt sich wie folgt beschreiben:
- Am Eingang liegt die binäre Quellensymbolfolge $〈q_k〉$ mit der Bitrate $R_{\rm B}$ an. Der zeitliche Abstand zweier Symbole ist damit $T_{\rm B} = 1/R_{\rm B}$.
- Aus jeweils $b$ binären Eingangssymbolen $q_k$ werden zwei mehrstufige Amplitudenkoeffizienten $a_{{\rm I}ν}$ und $a_{{\rm Q}ν}$ abgeleitet, wobei $\rm I$ für Inphase und $\rm Q$ für Quadraturkomponente steht.
- Ist $b$ geradzahlig und die Signalraumzuordnung quadratisch, so können die Koeffizienten $a_{{\rm I}ν}$ und $a_{{\rm Q}ν}$ jeweils einen von $M = 2^{b/2}$ Amplitudenwerten mit gleicher Wahrscheinlichkeit annehmen. Man spricht dann von Quadratur–Amplitudenmodulation $\rm (QAM)$.
- Das in der Grafik betrachtete Beispiel gilt für die $\text{16-QAM}$ mit $b = M = 4$ und dementsprechend $M^2 =16$ Signalraumpunkten. Bei einer $\text{256-QAM}$ würde $b = 8$ und $M = 16$ gelten: $2^b = M^2 = 256$.
- Anschließend werden die Koeffizienten $a_{{\rm I}ν}$ und $a_{{\rm Q}ν}$ jeweils einem Diracpuls als Impulsgewichte eingeprägt. Nach der Impulsformung mit dem Sendegrundimpuls $g_s(t)$ gilt somit in den beiden Zweigen des Blockschaltbildes:
- $$s_{\rm I}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\hspace{1cm}s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.$$
- Anzumerken ist, dass wegen der redundanzfreien Umsetzung die Symboldauer $T$ dieser Signale um den Faktor $b$ größer ist als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Im gezeichneten Beispiel $\text{(16-QAM)}$ gilt $T = 4 · T_{\rm B}$.
- Das QAM–Sendesignal $s(t)$ ist dann die Summe der beiden mit Cosinus bzw. Minus–Sinus multiplizierten Teilsignale:
- $$s_{\rm cos}(t) = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t), \hspace{1cm} s_{\rm -sin}(t) = -s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t)$$
- $$\Rightarrow \hspace{0.3cm}s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t) \hspace{0.05cm}.$$
$\text{Fazit:}$ Diese Aussagen können wie folgt zusammengefasst werden:
- Die beiden Übertragungszweige $\rm (I,\ Q)$ können als zwei völlig getrennte $M$–stufige ASK–Systeme aufgefasst werden, die sich gegenseitig nicht stören, solange alle Komponenten optimal ausgelegt sind.
- Die Quadratur–Amplitudenmodulation ermöglicht somit (im Idealfall) eine Verdoppelung der Datenrate bei gleichbleibender Qualität.
Systembeschreibung durch das äquivalente Tiefpass–Signal
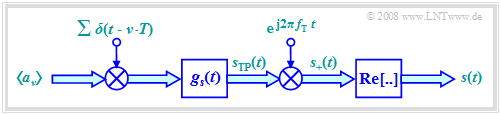
Da die Multiplikation von $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ mit einer Cosinus– bzw. Minus–Sinus–Schwingung nur eine Verschiebung im Frequenzbereich bewirkt und eine solche Verschiebung eine lineare Operation darstellt, lässt sich die Systembeschreibung mit Hilfe der äquivalenten Tiefpass–Signale wesentlich vereinfachen.
- Die Grafik zeigt das vereinfachte Modell im Basisband. Dieses ist äquivalent zum bisher betrachteten Blockschaltbild.
- Die im Blockschaltbild rot gezeichnete Seriell–Parallel–Wandlung und die Signalraumzuordnung bleibt erhalten. Dieser Block ist hier nicht mehr eingezeichnet.
- Wir lassen zunächst auch den oft aus schaltungstechnischen Gründen eingebrachten Bandpass $H_{\rm BP}(f)$ außer Betracht.
Beachten Sie bitte die folgenden Hinweise:
- Alle Doppelpfeile im Basisbandmodell kennzeichnen komplexe Größen. Die damit verbundenen Operationen sind ebenfalls komplex zu verstehen. Beispielsweise fasst der komplexe Amplitudenkoeffizient $a_ν$ je einen Inphase– und einen Quadraturkoeffizienten zusammen:
- $$a_\nu = a_{\rm I\hspace{0.03cm}\it \nu} + {\rm j} \cdot a_{\rm Q\hspace{0.03cm}\it \nu} \hspace{0.05cm}.$$
- Die äquivalente Tiefpass–Repräsentation des tatsächlichen, physikalischen und damit per se reellen Sendesignals $s(t)$ ist bei QAM stets komplex und es gilt mit den Teilsignalen $s_{\rm I}(t)$ und $s_{\rm Q}(t)$:
- $$s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} \cdot s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty} a_\nu \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.$$
- Zum analytischen Signal $s_+(t)$ kommt man von $s_{\rm TP}(t)$ durch Multiplikation mit der komplexen Exponentialfunktion. Das physikalische Sendesignal $s(t)$ ergibt sich dann als der Realteil von $s_+(t)$.
- Damit die Vorzeichen im Blockschaltbild der letzten Seite und im skizzierten Basisbandmodell übereinstimmen, ist im Quadraturzweig die Multiplikation mit der negativen Sinus–Schwingung erforderlich, wie die nachfolgende Rechnung zeigt:
- $$s(t) = {\rm Re}[s_{\rm +}(t)] = {\rm Re}[s_{\rm TP}(t) \cdot{\rm e}^{{\rm j}2\pi f_{\rm T} t}] $$
- $$\Rightarrow \hspace{0.3cm} s(t) = {\rm Re} \left[\left ( \sum (a_{\rm I\hspace{0.03cm}\it \nu} + {\rm j} \cdot a_{\rm Q\hspace{0.03cm}\it \nu} ) \cdot g_s (t - \nu \cdot T)\right )\left ( \cos(2 \pi f_{\rm T} t) + {\rm j} \cdot \sin(2 \pi f_{\rm T} t) \right )\right]= s_{\rm I}(t) \cdot \cos(2\pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t) \hspace{0.05cm}.$$
- Der Einfluss des Bandpasses $H_{\rm BP}(f)$, der in der Praxis oft am Ausgang des QAM–Modulators zu berücksichtigen ist, kann dem Impulsformfilter $g_s(t)$ beaufschlagt werden. Ist der Durchlassbereich des Bandpass–Filters symmetrisch um $f_{\rm T}$, so ist sein Tiefpass–Äquivalent (im Zeitbereich) $h_{\rm BP→TP}(t)$ rein reell und man kann im Modell $g_s(t)$ durch $g_s(t) \star h_{\rm BP→TP}(t)$ ersetzen.
Leistung und Energie von QAM–Signalen
Wie im Kapitel Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion im Buch „Signaldarstellung” gezeigt wird, kann die Leistung des QAM–Sendesignals $s(t)$ auch aus dem äquivalenten Tiefpass–Signal $s_{\rm TP}(t)$ berechnet werden, das stets komplex ist. Es gilt gleichermaßen:
- $$P = \lim_{T_{\rm M} \rightarrow \infty} \frac{\rm 1}{T_{\rm M}}\cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} s^2(t)\,{\rm d} t = {\rm 1}/{2} \cdot \lim_{T_{\rm M} \rightarrow \infty} \frac{\rm 1}{T_{\rm M}}\cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} |s_{\rm TP}(t)|^2\,{\rm d} t \hspace{0.05cm}.$$
Die Energie der zeitlich unbegrenzten Signale $s(t)$ und $s_{\rm TP}(t)$ ist dagegen unendlich groß.
Beschränkt man sich jedoch auf eine Symboldauer $T$, so erhält man die Energie pro Symbol:
- $$E_{\rm S} = \frac{{\rm E}[\hspace{0.05cm}|a_{\nu} |^2\hspace{0.05cm}]}{2}\cdot \int_{-\infty}^{+\infty} |g_s(t)|^2\,{\rm d} t = \frac{{\rm E}[|a_{\nu} |^2]}{2}\cdot \int_{-\infty}^{+\infty} |G_s(f)|^2\,{\rm d} f \hspace{0.05cm}.$$
Dagegen gibt $E_{\rm B} = E_{\rm S}/b$ die Energie pro Bit an, wenn man gemäß der Signalraumzuordnung jeweils $b$ Binärsymbole zum komplexen Koeffizienten $a_\nu$ zusammenfasst.
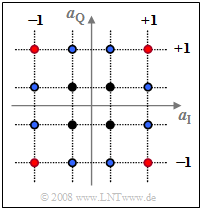
$\text{Beispiel 1:}$ Die obere Grafik zeigt die Signalraumzuordnung bei $\text{16-QAM}$, wobei sowohl der Real– als auch der Imaginärteil der komplexen Amplitudenkoeffizienten $a_ν$ jeweils einen von vier Werten $±1$ sowie $±1/3$ annehmen kann.
Die Mittelung über die $16$ Abstandsquadrate zum Ursprung ergibt:
- $${\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] \hspace{0.18cm} = \hspace{0.18cm} \frac{4}{16} \cdot (1^2 + 1^2)+ \frac{4}{16} \cdot \left[(1/3 )^2 +(1/3)^2 \right ] + \frac{8}{16} \cdot \left [1^2 + (1/3)^2\right ] $$
- $$\Rightarrow \hspace{0.3cm}{\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] = {10}/{9}\approx 1.11 \hspace{0.05cm}.$$
Die Summanden gehören in dieser Reihenfolge zu
- den vier roten,
- den vier schwarzen und
- den acht blauen Punkten.
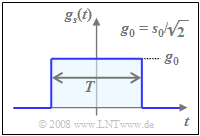
Bei NRZ–rechteckförmigem Sendegrundimpuls $g_s(t)$ mit der Amplitude $g_0$ und der Symboldauer $T$ ist das Spektrum $G_s(f)$ $\rm si$–förmig.
In diesem Fall gilt für
- die mittlere Energie pro Symbol:
- $$E_{\rm S} = 1/2 \cdot {\rm E}\big[\hspace{0.05cm}\vert a_{\nu} \vert ^2 \big]\hspace{0.05cm}\cdot g_0^2 \cdot T = {5}/{9}\cdot g_0^2 \cdot T \hspace{0.05cm}\approx 0.555 \cdot g_0^2 \cdot T \hspace{0.05cm},$$
- die mittlere Energie pro Bit:
- $$E_{\rm B} ={E_{\rm S} }/{4}= {5}/{36}\cdot g_0^2 \cdot T \approx 0.139 \cdot g_0^2 \cdot T \hspace{0.05cm}.$$
Die „maximale Hüllkurve” $s_0$ des Sendesignals $s(t)$ ist um den Faktor $\sqrt{2}$ größer als die Amplitude $g_0$ des Rechteckimpulses (siehe untere Skizze) und tritt bei einem der vier roten Amplitudenkoeffizienten auf, also immer dann, wenn $\vert a_{\rm I \it ν}\vert = \vert a_{\rm Q \it ν}\vert =1$ ist.
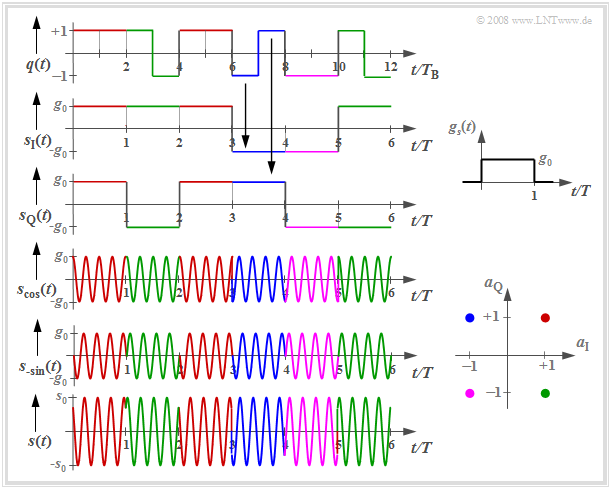
Signalverläufe der 4–QAM
Die folgende Grafik zeigt die Signalverläufe der $\rm 4-QAM$, wobei die Farbgebung mit der oben definierten Signalraumzuordnung übereinstimmt.
Man erkennt aus diesen Darstellungen:
- die Seriell–Parallel–Wandlung des Quellensignals $q(t)$ in die beiden Komponentensignale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$, jeweils mit der Symboldauer $T = 2T_{\rm B}$ und den Signalwerten $±g_0$. Hierbei bezeichnet $T_{\rm B}$ die Bitdauer;
- die beiden trägerfrequenzmodulierten Signale $s_{\rm cos}(t)$ und $s_{\rm –sin}(t)$ mit Phasensprüngen um $±π$:
- $$s_{\rm cos} (t) = s_{\rm I} (t) \cdot \cos(2\pi f_{\rm T}t)\hspace{0.05cm},$$
- $$s_{\rm -sin} (t) = -s_{\rm Q} (t) \cdot \sin(2\pi f_{\rm T}t)\hspace{0.05cm}, $$
- das Sendesignal $s(t) = s_{\rm cos}(t) \ – \ s_{\rm –sin}(t)$ mit Phasensprüngen um Vielfache von $±π/2$; deren Hüllkurve ist gegenüber den beiden Komponentensignalen um den Faktor $\sqrt{2}$ größer:
- $$s_0 = \sqrt{2} \cdot g_0 \hspace{0.05cm}.$$
- Der Sendegrundimpuls $g_s(t)$ ist hier zur Vereinfachung der Darstellung zwischen $0$ bis $T$ als rechteckförmig angenommen, also unsymmetrisch bezüglich $t = 0$.
- Die zugehörige Spektralfunktion $G_s(f)$ dieses kausalen Impulses $g_s(t)$ ist komplex, was jedoch in diesem Zusammenhang keine Auswirkungen hat.
Fehlerwahrscheinlichkeit der 4–QAM
Im früheren Abschnitt Fehlerwahrscheinlichkeiten – ein kurzer Überblick wurde unter anderem die Bitfehlerwahrscheinlichkeit der binären Phasenmodulation $($englisch: Binary Phase Shift Keying, $\rm BPSK)$ angegeben. Nun werden die Ergebnisse auf die $\text{4-QAM}$ übertragen, wobei weiterhin folgende Voraussetzungen gelten:
- ein Sendesignal mit der mittleren Energie $E_{\rm B}$ pro Bit,
- AWGN–Rauschen mit der (einseitigen) Rauschleistungsdichte $N_0$,
- bestmögliche Empfängerrealisierung nach dem Matched–Filter–Prinzip.
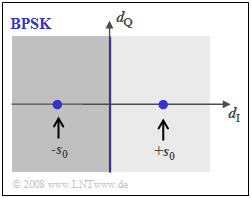
Die obere Abbildung zeigt das BPSK–Phasendiagramm des Detektionssignals $d(t)$, also inklusive dem Matched–Filter. Der Abstand des Nutzsignals von der Schwelle ($d_{\rm Q}$–Achse) beträgt zu den Detektionszeitpunkten jeweils $s_0$.
Mit den weiteren Gleichungen
- $$p_{\rm B} = {\rm Q}\left ( {s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$
erhält man für die BPSK–Fehlerwahrscheinlichkeit: $$p_{\rm B, \hspace{0.1cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
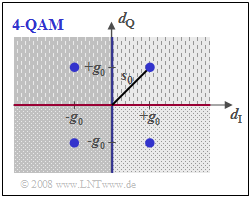
Bei der $\text{4-QAM}$ entsprechend der unteren Abbildung
- gibt es zwei Schwellen zwischen den Bereichen mit hellerem/dunklerem Hintergrund (blaue Linie) sowie zwischen den gepunkteten/gestrichelten Flächen (rote Linie),
- ist der Abstand von den Schwellen jeweils nur noch $g_0$ anstelle von $s_0$,
- ist aber die Rauschleistung $\sigma_d^2$ wegen der halben Symbolrate in jedem Teilzweig gegenüber der BPSK auch nur halb so groß.
Man erhält somit für die 4–QAM–Fehlerwahrscheinlichkeit mit den Gleichungen
- $$p_{\rm B} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}(2 \cdot T_{\rm B} )$$
genau das gleiche Ergebnis wie für die BPSK:
- $$p_{\rm B, \hspace{0.1cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
$\text{Fazit:}$
- Die $\text{4-QAM}$ hat bei idealen Bedingungen die gleiche Fehlerwahrscheinlichkeit wie die $\text{BPSK}$, obwohl die doppelte Informationsmenge übertragen werden kann.
- Sind allerdings die Bedingungen nicht mehr ideal – zum Beispiel bei einem ungewollten Phasenversatz zwischen Sender und Empfänger – so gibt es bei der 4–QAM eine deutlich stärkere Degradation als bei der BPSK.
- Dieser Fall wird im Abschnitt Fehlerwahrscheinlichkeit bei 4–QAM und BPSK des Buches „Digitalsignalübertragung” noch genauer betrachtet.
Quadratische QAM–Signalraumkonstellationen
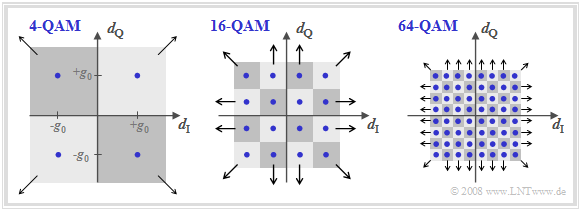
Die folgende Grafik zeigt die Signalraumkonstellationen von $\text{4-QAM}$, $\text{16-QAM}$ und $\text{64-QAM}$.
- Mit den hier gewählten Achsenbeschriftungen beschreiben die Bilder auch das Detektionsnutzsignal (zu den Detektionszeitpunkten) im äquivalenten Tiefpassbereich.
- Ebenfalls eingezeichnet sind die verschiedenen Entscheidungsgebiete, die dem verrauschten Detektionssignal zugeordnet werden.
- Die Pfeile geben an, wenn Entscheidungsgebiete bis ins Unendliche ausgedehnt sind.
Die Bilder beziehen sich nur auf die Detektionszeitpunkte und gelten für alle Nyquistsysteme
- wie die Rechteck–Rechteck–Konfiguration (Sendegrundimpuls und Empfangsfilter–Impulsantwort seien rechteckförmig)
- oder ein Wurzel–Cosinus–Rolloff–Nyquistsystem.
Die hier nicht dargestellten Übergänge zwischen den einzelnen Punkten (außerhalb der Detektionszeitpunkte) hängen aber sehr wohl vom gewählten Nyquistsystem ab.
Weiter ist zu diesen Darstellungen anzumerken:
- Bei echter QAM–Struktur – das heißt: die Signalraumkonstellation ist quadratisch oder zumindest rechteckförmig – lässt sich die „zweidimensionale” Detektion durch zwei „eindimensionale” Detektionsvorgänge vereinfacht lösen.
- Die $\text{16-QAM}$ ist somit nichts anderes als die parallele Übertragung zweier Digitalsignale mit jeweils $M = 4$ Amplitudenstufen.
- Bei der $\text{64-QAM}$ würde entsprechend $M = 8$ gelten und bei der $\text{256-QAM}$ ist die „eindimensionale” Stufenzahl $M = 16$.
- Alle im Kapitel Redundanzfreie Codierung des Buches „Digitalsignalübertragung” genannten Eigenschaften für redundanzfreie mehrstufige Signale gelten auch hier, wobei allerdings die Zusetzung der orthogoalen Trägerfrequenzsignale noch geeignet zu berücksichtigen ist.
Weitere Signalraumkonstellationen
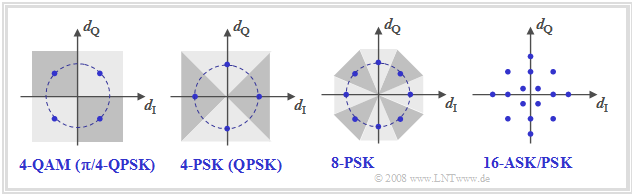
Die Grafik zeigt weitere Signalraumkonstellationen. Links ist die 4–QAM nach der bisherigen Beschreibung dargestellt. Die Konstellation rechts daneben kennzeichnet eine vierstufige Phasenmodulation, die wir „4–PSK” bzw. „QPSK” nennen. Ein Vergleich dieser beiden linken Diagramme zeigt:
- Die hier als QPSK (Quaternary Phase Shift Keying ) bezeichnete Variante verwendet die Phasenlagen $0^\circ$, $90^\circ$, $180^\circ$ und $270^\circ$.
- Aus den eingezeichneten Entscheidungsgebieten erkennt man, dass hier die Detektion nicht auf zwei Binärentscheidungen zurückgeführt werden kann.
- Auch die 4–QAM (links) kann als vierstufige Phasenmodulation aufgefasst werden $($Phasenlagen $±45^\circ$, $±135^\circ)$.
- Gegenüber der QPSK ergibt sich eine Drehung um $±45^\circ$ $(π/4)$ ⇒ die 4–QAM oft auch als ${\rm π/4}\text{–QPSK}$ bezeichnet.
- Ähnlich wie man bei der BPSK durch Vorcodierung zur DPSK kommt, kann auch die 4–PSK zur 4–DPSK erweitert und dadurch die Demodulation erleichtert werden.
- Diese wurde zum Beispiel bei der Datenübertragung über Telefonkanäle gemäß CCITT–Empfehlung „V26” angewendet $($Trägerfrequenz $\text{1800 Hz}$, Datenrate $\text{2400 bit/s)}$.
Die beiden rechten Diagramme zeigen höherstufige Modulationsverfahren:
- Die 8–PSK (bzw. 8–DPSK) erlaubt entsprechend der CCITT–Empfehlung „V27” beim Telefonkanal eine Datenrate von bis zu $\text{4800 bit/s}$.
- Die Empfehlung „V29” sieht mit der 16–ASK/PSK eine hybride Modulationsform vor, die bei fest verschalteten Leitungen Datenraten bis $\text{9600 bit/s}$ ermöglicht.
Nyquist– und Wurzel–Nyquist–QAM–Systeme
Bisher wurde in diesem Kapitel aus Darstellungsgründen stets vom rechteckförmigen Sendegrundimpuls ausgegangen. In der Praxis verwendet man aber meist eine Wurzel–Nyquist–Charakteristik entsprechend der Beschreibung im Buch „Digitalsignalübertragung”. In aller Kürze lassen sich diese Systeme wie folgt charakterisieren:
- Der Empfängerfrequenzgang $H_{\rm E}(f)$ wird hier formgleich mit dem (normierten) Sendeimpulsspektrum $H_{\rm S}(f)$ gewählt, was unter der Nebenbedingung der Leistungsbegrenzung (das heißt: bei konstanter mittlerer Sendeleistung) zur kleinstmöglichen Fehlerwahrscheinlichkeit führt.
- Der Gesamtfrequenzgang $H_{\rm Nyq}(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt das erste Nyquistkriterium, so dass es beim Empfänger zu keinen Impulsinterferenzen kommt. $H_{\rm S}(f)$ und $H_{\rm E}(f)$ haben somit jeweils eine Wurzel–Nyquist–Charakteristik.
- Für den Frequenzgang $H_{\rm Nyq}(f)$ verwendet man einen Cosinus–Rolloff–Tiefpass $H_{\rm CRO}(f)$ mit der äquivalenten Bandbreite $Δf_{\rm CRO} = 1/T$ und frei wählbarem Rolloff–Faktor $(0 ≤ r ≤ 1)$. Das interaktive Applet Frequenzgang und Impulsantwort verdeutlicht den Frequenzgang und die Impulsantwort dieses Tiefpasses.
- Der Vorteil dieser Wurzel–Nyquist–Systeme ist die deutlich kleinere Bandbreite $(1 + r)/T$ gegenüber der bisher betrachteten Konfiguration mit rechteckförmigem $g_s(t)$ und rechteckförmigem $h_{\rm E}(t)$, dessen Spektrum (theoretisch) unendlich weit ausgedehnt ist.
- Hinsichtlich Fehlerwahrscheinlichkeit ändert sich gegenüber der Rechteck–Rechteck–Konfiguration nichts, da der Grundimpuls $g_d(t)$ vor dem Entscheider äquidistante Nulldurchgänge aufweist und somit Impulsinterferenzen vermieden werden.
Die Grafik zeigt die Phasendiagramme für diesen Fall, die dem Buch [Kam04][1] entnommen sind. Der Rolloff–Faktor beträgt $r = 0.5$. Man erkennt aus diesen Darstellungen:
- Das rechte Diagramm zeigt die Detektionssignale im $\rm I$– und $\rm Q$–Zweig nach den Wurzel–Nyquist–Empfangsfiltern in 2D–Darstellung. Die dazugehörigen Spektren besitzen jeweils cosinusförmige Flanken um die Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$.
- Zu den Detektionszeitpunkten sind im Phasendiagramm nur die vier gelb eingezeichneten Punkte möglich. Die Übergänge dazwischen sind vielfältig. Anzumerken ist, dass nur wenige Linien durch den Koordinaten-Nullpunkt gehen.
- Links dargestellt sind die beiden Sendesignale im äquivalenten Tiefpassbereich, $s_{\rm I}(t) = {\rm Re}\big[s_{\rm TP}(t)\big]$ und $s_{\rm Q}(t) = {\rm Im}\big[s_{\rm TP}(t)\big]$. Aufgrund der Wurzel–Nyquist–Spektralformung gibt es beim Sender Impulsinterferenzen, das heißt, dass das äquivalente Tiefpass–Signal $s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} · s_{\rm Q}(t)$ auch zu den Detektionszeitpunkten nicht auf vier Punkte beschränkt ist.
- Der Betrag $|s_{\rm TP}(t)|$ – also der Abstand vom Nullpunkt – gibt die Hüllkurve des 4–QAM–Signals an. Man erkennt aus dem linken Diagramm deutlich, dass es insbesondere bei Phasenänderungen um $π$ starke Amplitudeneinbrüche gibt, da $s_{\rm TP}(t)$ dann auch (komplexe) Werte nahe Null annimmt.
Offset–Quadraturamplitudenmodulation
Ausgehend von den Gleichungen für die 4–QAM (bzw. $π/4$–QPSK) kommt man zur Offset–4–QAM, die wir vereinfachend mit Offset–QPSK $($kurz: O–QPSK$)$ bezeichnen. Für das Sendesignal gilt hier:
- $$s(t) =s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t),$$
- $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm I}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\hspace{0.5cm} s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it \nu} \cdot g_s (t -{T}/{2} - \nu \cdot T)\hspace{0.05cm}.$$
Der einzige, aber entscheidende Unterschied ist die zeitliche Verschiebung der Quadraturkomponente gegenüber der Inphasekomponente um eine halbe Symboldauer $(T/2)$. Dies hat den Vorteil, dass
- die Phasenfunktion nicht durch Null geht, und
- dadurch die Hüllkurve $|s_{\rm TP}(t)|$ auch deutlich weniger schwankt.
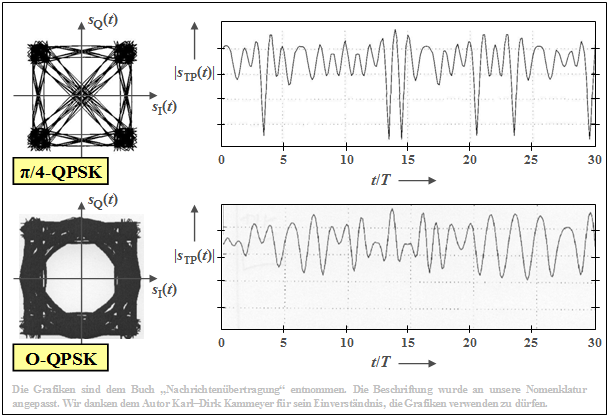
$\text{Beispiel 2:}$ Die Grafik zeigt oben nochmals das Phasendiagramm für die 4–QAM $(π$/4–QPSK$)$ und rechts daneben einen beispielhaften Verlauf der Hüllkurve, wobei wie im letzten Abschnitt ein Wurzel–Nyquist–Sendespektrum mit dem Rolloff–Faktor $r = 0.5$ zugrunde liegt.
Die beiden unteren Bilder zeigen, dass die Offset–QPSK hinsichtlich der Einhüllenden deutlich bessere Eigenschaften (weniger gravierende Signaleinbrüche) besitzt.
Wesentliche Eigenschaften von 4–QAM/QPSK und Offset–QPSK können Sie sich mit dem interaktiven Applet QPSK und Offset-QPSK verdeutlichen, wobei als Grundimpuls alternativ wählbar ist:
- ein Rechteckimpuls,
- ein Cosinusimpuls,
- ein Nyquistimpuls,
- ein Wurzel–Nyquistimpuls.
Aufgaben zum Kapitel
Aufgabe 4.10: Signalverläufe der 16–QAM
Aufgabe 4.10Z: Signalraumkonstellation der 16–QAM
Aufgabe 4.11: Frequenzbereichsbetrachtung der 4–QAM
Aufgabe 4.11Z: Fehlerwahrscheinlichkeit bei QAM
Aufgabe 4.12: Wurzel–Nyquist–Systeme
Aufgabe 4.12Z: Nochmals 4–QAM–Systeme
Quellenverzeichnis
- ↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.