Applets:Prinzip der 4B3T-Codierung: Unterschied zwischen den Versionen
| Zeile 136: | Zeile 136: | ||
* Für die nächsten vier Binärsymbole ist nun von ${\it \Sigma}_1= 2$ auszugehen: $(1, 0, 1, 1)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 3.$ | * Für die nächsten vier Binärsymbole ist nun von ${\it \Sigma}_1= 2$ auszugehen: $(1, 0, 1, 1)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 3.$ | ||
*Die Codierung der Binärsymbole 9 bis 12 ergibt sich mit ${\it \Sigma}_2= 3$ zu $(0, 1, 1, 0,)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 2.$ | *Die Codierung der Binärsymbole 9 bis 12 ergibt sich mit ${\it \Sigma}_2= 3$ zu $(0, 1, 1, 0,)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 2.$ | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' | + | '''(2)''' Wiederholen Sie diesen Versuch mit den anderen möglichen RDS-Startwerten ${\it \Sigma}_0= 1$, ${\it \Sigma}_0= 2$ und ${\it \Sigma}_0= 3.$ Wie unterscheiden sich die Codierergebnisse? }} |
| − | * | + | *${\it \Sigma}_0= 1$: $(0, 1, 0, 1)\ \rightarrow\ (0,\ - ,\ 0) $ ⇒ ${\it \Sigma}_1= 0$: $(1, 0, 1, 1)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 1$: $(0, 1, 1, 0,)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 0.$ |
| − | + | *${\it \Sigma}_0= 2$: $(0, 1, 0, 1)\ \rightarrow\ (0,\ - ,\ 0) $ ⇒ ${\it \Sigma}_1= 1$: $(1, 0, 1, 1)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 2$: $(0, 1, 1, 0,)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 1.$ | |
| + | *${\it \Sigma}_0= 3$: $(0, 1, 0, 1)\ \rightarrow\ (0,\ - ,\ 0) $ ⇒ ${\it \Sigma}_1= 2$: $(1, 0, 1, 1)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 3$: $(0, 1, 1, 0,)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 2.$ | ||
Version vom 18. September 2020, 15:29 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Das Applet behandelt die Eigenschaften der bekanntesten Pseudoternärcodes, nämlich:
- Bipolarcode erster Ordnung bzw. $\rm AMI$–Code (von: Alternate Mark Inversion), gekennzeichnet durch die Parameter $N_{\rm C} = 1, \ K_{\rm C} = +1$,
- Duobinärcode, $(\rm DUOB)$, Codeparameter: $N_{\rm C} = 1, \ K_{\rm C} = -1$,
- Bipolarcode zweiter Ordnung $(\rm BIP2)$, Codeparameter: $N_{\rm C} = 2, \ K_{\rm C} = +1$.
Am Eingang liegt die redundanzfreie binäre bipolare Quellensymbolfolge $\langle \hspace{0.05cm}q_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$ ⇒ Rechtecksignal $q(t)$ an. Verdeutlicht wird die Generierung
- der binär–vorcodierten Folge $\langle \hspace{0.05cm}b_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$, dargestellt durch das ebenfalls redundanzfreie binäre bipolare Rechtecksignal $b(t)$,
- der pseudoternären Codefolge $\langle \hspace{0.05cm}c_\nu \hspace{0.05cm}\rangle \ \in \{+1,\ 0, -1\}$, dargestellt durch das redundante ternäre bipolare Rechtecksignal $c(t)$,
- das gleichermaßen redundante ternäre Sendesignal $s(t)$, gekennzeichnet durch die Amplitudenkoeffizienten $a_\nu $, und den (Sende–) Grundimpuls $g(t)$:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$
Der Grundimpuls $g(t)$ – im Applet „Rechteck”, „Nyquist” und „Wurzel–Nyquist” – bestimmt nicht nur die Form des Sendesignals, sondern auch den Verlauf
- der Autokorrelationsfunktion $\rm (AKF)$ $\varphi_s (\tau)$ und
- des zugehörigen Leistungsdichtespektrums $\rm (LDS)$ ${\it \Phi}_s (f)$.
Das Applet zeigt auch, dass das gesamte Leistungsdichtespektrum ${\it \Phi}_s (f)$ aufgeteilt werden kann in den Anteil ${\it \Phi}_a (f)$, der die statistischen Bindungen der Amplitudenkoeffizienten $a_\nu$ berücksichtigt, und das Energiedichtespektrum $ {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 $, gekennzeichnet durch die Impulsform $g(t)$.
Anmerkung: Im Applet wird kein Unterschied zwischen den Codersymbolen $c_\nu \in \{+1,\ 0, -1\}$ und den Amplitudenkoeffizienten $a_\nu \in \{+1,\ 0, -1\}$ gemacht. Dabei sollte nicht vergessen werden, dass die $a_\nu$ stets Zahlenwerte sind, während für die Codersymbole auch die Notation $c_\nu \in \{\text{Plus},\ \text{Null},\ \text{Minus}\}$ zulässig wäre.
Theoretischer Hintergrund
Klassifizierung verschiedener Codierverfahren
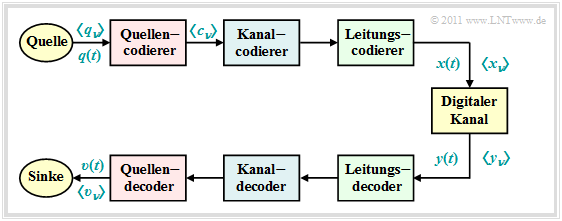
Wir betrachten das dargestellte digitale Übertragungsmodell. Wie aus diesem Blockschaltbild zu erkennen ist, unterscheidet man je nach Zielrichtung zwischen drei verschiedenen Arten von Codierung, jeweils realisiert durch den sendeseitigen Codierer (Coder) und den zugehörigen Decodierer (Decoder) beim Empfänger:
- $\text{Quellencodierung:}$ Entfernen (unnötiger) Redundanz, um Daten möglichst effizient speichern oder übertragen zu können ⇒ Datenkomprimierung. Beispiel: Differentielle Pulscodemodulation $\rm (DPCM)$ in der Bildcodierung.
- $\text{Kanalcodierung:}$ Gezieltes Hinzufügen (sinnvoller) Redundanz, die man beim Empfänger zur Fehlererkennung oder zur Fehlererkennung nutzen kann. Wichtigste Vertreter: Blockcodes, Faltungscodes, Turbocodes.
- $\text{Leitungscodierung:}$ Umcodierung der Quellensymbole, um das zu übertragende Signal an die spektralen Eigenschaften von Kanal und Empfangseinrichtungen anzupassen, etwa, um bei einem Kanal mit $H_{\rm K}(f = 0) = 0$ ein gleichsignalfreies Sendesignal zu erreichen.
Bei den Leitungscodes unterscheidet man weiter:
- $\text{Symbolweise Codierung:}$ Mit jedem ankommenden Binärsymbol $q_ν$ wird ein mehrstufiges (zum Beispiel: ternäres) Codesymbol $c_ν$ erzeugt, das auch von den vorherigen Binärsymbolen abhängt. Die Symboldauern $T_q$ und $T_c$ sind hierbei identisch. Beispiel: Pseudoternärcodes (AMI–Code, Duobinärcode).
- $\text{Blockweise Codierung:}$ Ein Block aus $m_q$ Binärsymbolen $(M_q = 2)$ wird durch eine Sequenz aus $m_c$ höherstufigen Symbolen $(M_c > 2)$ ersetzt. Ein Kennzeichen dieser Codeklasse ist $T_c> T_q$. Beispiele sind redundanzfreie Mehrstufencodes $(M_c$ ist eine Zweierpotenz$)$ sowie die hier betrachteten $\text{4B3T-Codes}$.
Allgemeine Beschreibung der 4B3T–Codes
Der bekannteste Blockcode zur Übertragungscodierung ist der $\rm 4B3T–Code$ mit den Codeparametern
- $$m_q = 4,\hspace{0.2cm}M_q = 2,\hspace{0.2cm}m_c = 3,\hspace{0.2cm}M_c = 3\hspace{0.05cm},$$
der bereits in den 1970–er Jahren entwickelt wurde und beispielsweise bei ISDN (Integrated Services Digital Networks ) eingesetzt wird.
Ein 4B3T–Code besitzt folgende Eigenschaften:
- Wegen $m_q \cdot T_{\rm B} = m_c \cdot T$ ist die Symboldauer $T$ des Codersignals um den Faktor $4/3$ größer als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Daraus ergibt sich die günstige Eigenschaft, dass der Bandbreitenbedarf um ein Viertel geringer ist als bei redundanzfreier Binärübertragung.
- Die relative Redundanz der 4B3T–Codes ergibt sich zu
- $$r_c = 1- \frac{m_q \cdot {\rm log_2}\hspace{0.05cm} (M_q)}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{4 \cdot {\rm log_2}\hspace{0.05cm} (2)}{3 \cdot {\rm log_2} \hspace{0.05cm}3}= 1- \frac{4 }{3 \cdot 1.585}\hspace{0.05cm}\approx{0.158}.$$
- Diese Redundanz von knapp $16\%$ wird dazu verwendet, um Gleichsignalfreiheit zu erzielen. Das 4B3T–codierte Signal kann somit ohne merkbare Beeinträchtigung auch über einen Kanal mit der Eigenschaft $H_{\rm K}(f)= 0) = 0$ übertragen werden.
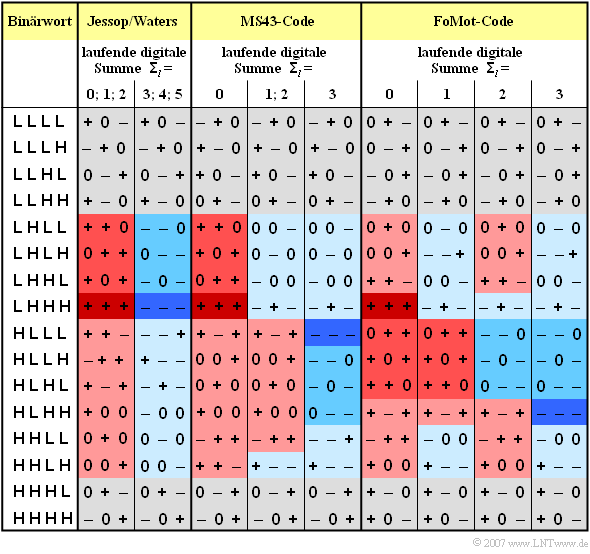
Die Umcodierung der sechzehn möglichen Binärblöcke in die entsprechenden Ternärblöcke könnte prinzipiell nach einer festen Codetabelle vorgenommen werden. Um die spektralen Eigenschaften dieser Codes weiter zu verbessern, werden bei den gebräuchlichen 4B3T–Codes, nämlich
- dem 4B3T–Code nach Jessop und Waters,
- dem MS43–Code (von: $\rm M$onitored $\rm S$um $\rm 4$B$\rm 3$T–Code),
- dem FoMoT–Code (von: $\rm Fo$ur $\rm Mo$de $\rm T$ernary),
zwei oder mehrere Codetabellen verwendet, deren Auswahl von der „laufenden digitalen Summe” der Amplitudenkoeffizienten gesteuert wird.
Laufende digitale Summe
Die ternären Amplitudenkoeffizienten seien $a_\nu \in \{ -1, \ 0, +1\}$. Nach der Übertragung von l Blöcken gilt für die „laufende digitale Summe”:
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu \hspace{0.05cm}.$$
Die Auswahl der Tabelle zur Codierung des $(l + 1)$–ten Blocks erfolgt abhängig vom aktuellen Wert ${\it \Sigma}_l$.
In der Tabelle sind die Codierregeln für die drei oben genannten 4B3T–Codes angegeben. Zur Vereinfachung der Schreibweise steht „+” für den Amplitudenkoeffizienten „+1” und „–” für den Koeffizienten „–1”.
- Die zwei Codetabellen des Jessop–Waters–Codes sind so gewählt, dass die laufende digitale Summe ${\it \Sigma}_l$ stets zwischen $0$ und $5$ liegt.
- Bei den beiden anderen Codes (MS43, FoMoT) erreicht man durch drei bzw. vier alternative Tabellen die Beschränkung der laufenden digitalen Summe auf den Wertebereich $0 \le {\it \Sigma}_l \le 3$.
Im Applet werden betrachtet:
- der $\rm MS43$–Code (von: $\rm M$odified $\rm M$onitored $\rm S$um $\rm 4$B$\rm 3$T–Code),
- der $\rm MMS43$–Code (von: $\rm M$odified $\rm MS43$).
Die „laufende digitale Summe” (englisch: Running Digital Sum) wird im Applet wie folgt bezeichnet:
- $${\it \Sigma}_l \ \Rightarrow \ {\rm RDS}_l .$$
AKF und LDS der 4B3T–Codes
Die Vorgehensweise zur Berechnung von AKF und LDS wird hier nur stichpunktartig skizziert. Im Applet wird hierauf nicht eingegangen):
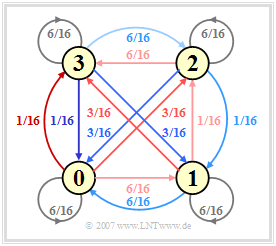
(1) Der Übergang der laufenden digitalen Summe von ${\it \Sigma}_l$ nach ${\it \Sigma}_{l+1}$ wird durch eine homogene stationäre Markovkette erster Ordnung mit sechs (Jessop–Waters) bzw. vier Zuständen (MS43, FoMoT) beschrieben. Für den FoMoT–Code gilt das rechts skizzierte Markovdiagramm.
(2) Die Werte an den Pfeilen kennzeichnen die Übergangswahrscheinlichkeiten ${\rm Pr}({\it \Sigma}_{l+1}|{\it \Sigma}_{l})$, die sich aus den jeweiligen Codetabellen ergeben. Die Farben korrespondieren zu den Hinterlegungen der Tabelle auf der letzten Seite. Aufgrund der Symmetrie des FoMoT–Markovdiagramms sind die vier Wahrscheinlichkeiten alle gleich:
- $${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}({\it \Sigma}_{l} = 3) = 1/4.$$
(3) Die Autokorrelationsfunktion (AKF) $\varphi_a(\lambda) = {\rm E}\big [a_\nu \cdot a_{\nu+\lambda}\big ]$ der Amplitudenkoeffizienten kann aus diesem Diagramm ermittelt werden. Einfacher als die analytische Berechnung, die eines sehr großen Rechenaufwands bedarf, ist die simulative Bestimmung der AKF–Werte mittels Computer.
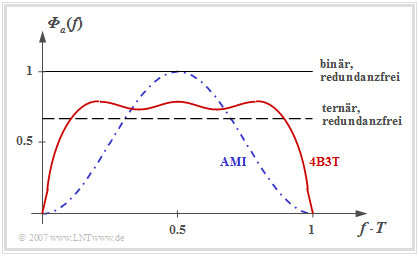
Durch Fouriertransformation der AKF kommt man zum Leistungsdichtespektrum (LDS) ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten entsprechend der folgenden Grafik aus [ST85][1]. Das skizzierte LDS wurde für den FoMoT–Code ermittelt, dessen Markovdiagramm oben dargestellt ist. Die Unterschiede der einzelnen 4B3T–Codes sind nicht sonderlich ausgeprägt. So gilt für den MS43–Code ${\rm E}\big [a_\nu^2 \big ] \approx 0.65$ und für die beiden anderen 4B3T-Codes (Jessop/Waters, MS43) ${\rm E}\big [a_\nu^2 \big ] \approx 0.69$.
Die Aussagen dieser Grafik kann man wie folgt zusammenfassen:
- Die Grafik zeigt das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten $a_\nu$ des 4B3T-Codes ⇒ rote Kurve.
- Das LDS ${\it \Phi}_s(f)$ unter Einbeziehung des Sendegrundimpulses erhält man durch Multiplikation mit $1/T \cdot |G_s(f)|^2$. Beispielsweise muss man ${\it \Phi}_a(f)$ mit einer $\rm si^2$–Funktion multiplizieren, wenn $g_s(t)$ einen Rechteckimpuls beschreibt.
- Bei redundanzfreier Binär– oder Ternärcodierung ergibt sich jeweils ein konstantes ${\it \Phi}_a(f)$, dessen Höhe von der Stufenzahl $M$ abhängt (unterschiedliche Signalleistung).
- Dagegen weist das 4B3T–Leistungsdichtespektrum Nullstellen bei $f = 0$ und Vielfachen von $f = 1/T$ auf.
- Die Nullstelle bei $f = 0$ hat den Vorteil, dass das 4B3T–Signal ohne große Einbußen auch über einen so genannten Telefonkanal übertragen werden kann, der aufgrund von Übertragern für ein Gleichsignal nicht geeignet ist.
- Die Nullstelle bei $f = 1/T$ hat den Nachteil, dass dadurch die Taktrückgewinnung am Empfänger erschwert wird. Außerhalb dieser Nullstellen weisen die 4B3T–Codes ein flacheres ${\it \Phi}_a(f)$ auf als der im nächsten Kapitel behandelte AMI–Code (blaue Kurve), was von Vorteil ist.
- Der Grund für den flacheren LDS–Verlauf bei mittleren Frequenzen sowie den steileren Abfall zu den Nullstellen hin ist, dass bei den 4B3T–Codes bis zu fünf $+1$– bzw. $-1$–Koeffizienten aufeinanderfolgen können. Beim AMI–Code treten diese Symbole nur isoliert auf.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, 2, ... ) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer 0 entspricht einem „Reset”: Einstellung wie beim Programmstart.
(1) Verdeutlichen Sie sich die 4B3T–Codierung der Quellensymbolfolge $\rm A$ ⇒ $\langle q_\nu \rangle = \langle 0, 1, 0, 1; \ 1, 0, 1, 1; \ 0, 1, 1, 0 \rangle $ gemäß dem MS43–Code im Schrittmodus.
Der RDS-Startwert sei ${\it \Sigma}_0= 0$. Hinweis: Die Quellensymbolfolge ist durch Semikola bereits in Teilfolgen mit jeweils vier Binärsymbolen unterteilt.
- Ausgehend vom RDS-Startwert ${\it \Sigma}_0= 0$ erkennt man folgende Codierung der ersten vier Binärsymbole: $(0, 1, 0, 1)\ \rightarrow\ (+,\ 0 ,\ +) $ ⇒ ${\it \Sigma}_1= 2.$
- Für die nächsten vier Binärsymbole ist nun von ${\it \Sigma}_1= 2$ auszugehen: $(1, 0, 1, 1)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 3.$
- Die Codierung der Binärsymbole 9 bis 12 ergibt sich mit ${\it \Sigma}_2= 3$ zu $(0, 1, 1, 0,)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 2.$
(2) Wiederholen Sie diesen Versuch mit den anderen möglichen RDS-Startwerten ${\it \Sigma}_0= 1$, ${\it \Sigma}_0= 2$ und ${\it \Sigma}_0= 3.$ Wie unterscheiden sich die Codierergebnisse?
- ${\it \Sigma}_0= 1$: $(0, 1, 0, 1)\ \rightarrow\ (0,\ - ,\ 0) $ ⇒ ${\it \Sigma}_1= 0$: $(1, 0, 1, 1)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 1$: $(0, 1, 1, 0,)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 0.$
- ${\it \Sigma}_0= 2$: $(0, 1, 0, 1)\ \rightarrow\ (0,\ - ,\ 0) $ ⇒ ${\it \Sigma}_1= 1$: $(1, 0, 1, 1)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 2$: $(0, 1, 1, 0,)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 1.$
- ${\it \Sigma}_0= 3$: $(0, 1, 0, 1)\ \rightarrow\ (0,\ - ,\ 0) $ ⇒ ${\it \Sigma}_1= 2$: $(1, 0, 1, 1)\ \rightarrow\ (+,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_2= 3$: $(0, 1, 1, 0,)\ \rightarrow\ (-,\ 0 ,\ 0) $ ⇒ ${\it \Sigma}_3= 2.$
(3) Betrachten Sie nun die AMI–Codierung für mehrere Zufallsfolgen. Welche Regeln lassen sich aus diesen Versuchen für die Ampltitudenkoeffizienten $a_\nu$ ableiten?
- Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Koeffizienten $a_\nu = 0$ codiert. Es können beliebig viele $a_\nu = 0$ aufeinanderfolgen.
- Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt, beginnend mit $a_\nu = -1$, falls $b_0 = +1$.
- Aus der Quellensymbolfolge $\rm A$ ⇒ $\langle \hspace{0.05cm}q_\nu \equiv +1 \hspace{0.05cm}\rangle$ wird die Codesymbolfolge $+1, -1, +1, -1, \text{...}$ . Lange Folgen $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$ bzw. $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$ sind ausgeschossen.
(4) Weiterhin AMI–Codierung. Interpretieren Sie die Autokorrelationsfunktion $\varphi_a(\lambda)$ der Amplitudenkoeffizienten und das Leistungsdichtespektrum $\Phi_a(f)$.
- Die diskrete AKF $\varphi_a(\lambda)$ der Amplitudenkoeffizienten ist nur für ganzzahlige $\lambda$–Werte definiert. Beim AMI–Code $(N_{\rm C}=1)$ sind für $|\lambda| > 1$ alle $\varphi_a(\lambda)= 0$.
- $\varphi_a(\lambda = 0)$ ist gleich dem quadratischen Mittelwert der Amplitudenkoeffizienten ⇒ $\varphi_a(\lambda = 0) = {\rm Pr}(a_\nu = +1) \cdot (+1)^2 + {\rm Pr}(a_\nu = -1) \cdot (-1)^2 = 0.5.$
- Zum Erwartungswert ${\rm E}\big [a_\nu \cdot a_{\nu+1}\big]$ tragen nur die Kombinationen $(+1, -1)$ und $(-1, +1)$ bei. Ergebnis: $\varphi_a(\lambda = \pm 1)={\rm E}\big [a_\nu \cdot a_{\nu+1}\big]=-0.25.$
- Das Leistungsdichtespektrum ${\it \Phi}_a(f)$ ist die Fouriertransformierte der diskreten AKF $\varphi_a(\lambda)$. Das Ergebnis ist ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$
- Aus der Gleichsignalfreiheit ⇒ ${\it \Phi}_a(f = 0) = 0$ folgt: Der AMI–Code ist insbesondere für Kanäle interessant, über die kein Gleichanteil übertragen werden kann.
(5) Wir betrachten weiter die AMI–Codierung und den Rechteckimpuls. Interpretieren Sie die AKF $\varphi_s(\tau)$ des Sendesignals und das LDS ${\it \Phi}_s(f)$.
- $\varphi_s(\tau)$ ergibt sich aus der Faltung der diskreten AKF $\varphi_a(\lambda)$ mit $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$. Beim Rechteckimpuls $($Dauer $T)$ ist die Energie–AKF $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$ ein Dreieck der Dauer $2T$.
- Es gilt $\varphi_s(\tau = 0)= \varphi_a(\lambda = 0) =0.5, \ \varphi_s(\pm T)= \varphi_a( 1) =-0.25,\ , \ \varphi_s( \pm 2T)= \varphi_a(2) =0.$ Zwischen diesen diskreten Werten verläuft $\varphi_{s}(\tau)$ stets linear.
- Das LDS ${\it \Phi}_s(f)$ ergibt sich aus ${\it \Phi}_a(f) = \sin^2(\pi f T)$ durch Multiplikation mit ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = {\rm si}^2(\pi f T).$ An den Nullstellen von ${\it \Phi}_a(f)$ ändert sich dadurch nichts.
(6) Was ändert sich bezüglich $s(t)$, $\varphi_s(\tau)$ und ${\it \Phi}_s(f)$ mit dem Nyquistimpuls? Variieren Sie hierbei den Rolloff–Faktor im Bereich $0 \le r \le 1$.
- Ein einzelner Nyquistimpuls kann mit der Quellensymbolfolge $\rm B$ im $s(t)$–Bereich dargestellt werden. Man erkennt die äquidistanten Nulldurchgänge im Abstand $T$.
- Auch bei jeder AMI–Zufallsfolge entsprechen die Signalwerte $s(t=\nu \cdot T)$ für jedes $r$ genau ihren Solllagen. Außerhalb dieser Punkte gibt es Abweichungen.
- Im Sonderfall $r=0$ ist das Energie–LDS ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$ im Bereich $|f|<1/2T$ konstant. Dementsprechend hat die Energie–AKF ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ einen $\rm si$–förmigen Verlauf.
- Bei größerem $r$ sind dagegen die Nullstellen von ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ nicht mehr äqidistant, da zwar $G(f)$ das erste Nyquistkriterium erfüllt, aber nicht ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$.
- Der wesentliche Vorteil des Nyquistimpulses ist die deutlich kleinere Bandbreite. Hier muss nur der Frequenzbereich $|f| < (1+r)/(2T)$ bereitgestellt werden.
(7) Wiederholen Sie den letzten Versuch mit dem Wurzel–Nyquistimpuls anstelle des Nyquistimpulses und interpretieren Sie die Ergebnisse.
- Im Sonderfall $r=0$ sind die Ergebnisse wie in (6). ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$ ist im Bereich $|f|<1/2T$ konstant, außerhalb Null; ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ hat einen $\rm si$–förmigen Verlauf.
- Auch bei größerem $r$ sind die Nullstellen von ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$ äqidistant (aber nicht $\rm si$–förmig) ⇒ ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$ erfüllt das erste Nyquistkriterium.
- Dagegen erfüllt $G(f)$ das erste Nyquistkriterium nicht $($außer für $r=0)$. Es kommt vielmehr bereits beim Sendesignal $s(t)$ zu Impulsinterferenzen.
- Dies ist aber auch kein grundlegendes Problem. Durch ein formgleiches Empfangsfilter wie $G(f)$ werden Impulsinterferenzen vor dem Entscheider vermieden.
(8) Betrachten und kontrollieren Sie die Vorcodierung $(b_\nu)$ und die Amplitudenoeffizienten $a_\nu$ beim Duobinärcode $($Quellensymbolfolge $\rm C$, $b_0 = +1)$.
- $b_1 = (q_1 = +1)\ {\rm XOR}\ (\overline{b_0}= -1) = +1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (\overline{b_1}= -1) = -1,\ \ b_3 = \text{...} =b_7 = +1,$ $b_8 = b_{10} = \text{...} =-1$, $b_9 =b_{11} = \text{...}= +1$.
- $a_1= 0.5 \cdot (b_1+b_0) = +1$, $a_2= 0.5 \cdot (b_2+b_1) =0$, $a_3= 0.5 \cdot (b_3+b_2) = 0$, $a_4= \text{...}= a_7=+1$, $a_8=a_9= \text{...}= 0$.
- Mit der Startbedingung $b_0 = -1$ ergibt sich wieder die negierte Folge: $a_1= -1$, $a_2= a_3= 0$, $a_4= \text{...}= a_7=-1$, $a_8=a_9= \text{...}= 0$.
(9) Betrachten Sie nun die Duobinärodierung für mehrere Zufallsfolgen. Welche Regeln lassen sich aus diesen Versuchen für die Ampltitudenkoeffizienten $a_\nu$ ableiten?
- Die diskreten AKF–Werte sind $\varphi_a(\lambda = 0) = +0.5$, $\varphi_a(\lambda = 1) = +0.25$, $\varphi_a(\lambda = 2) = 0$ ⇒ ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm}.$
- Im Gegensatz zur AMI–Codierung sind hier längere $+1$–Folgen und $-1$–Folgen möglich ⇒ der Duobinärcode ist nicht gleichsignalfrei: ${\it \Phi}_a(f= 0) = 1 \ (\ne 0).$
- Ebenso wie beim AMI–Code sind auch hier längere Nullfolgen möglich, was wieder zu Synchronisationsproblemen führen kann.
- Ausgeschlossen sind jedoch die Kombinationen $a_\nu = +1, \ a_{\nu+1} = -1$ und $a_\nu = -1, \ a_{\nu+1} = +1$, erkennbar am LDS–Wert ${\it \Phi}_a(f= 1/(2T)) = 0.$
- Solche direkten Übergänge $a_\nu = +1$ ⇒ $a_{\nu+1} = -1$ bzw. $a_\nu = -1$ ⇒ $a_{\nu+1} = +1$ führen zu großen Impulsinterferenzen und damit zu einer höheren Fehlerrate.
(10) Vergleichen Sie die Codierergebnisse von Bipolarcode zweiter Ordnung $\rm (BIP2)$ und AMI–Code für verschiedene Quellensymbolfolgen.
- Bei einem einzelnen $+1$–Impuls ⇒ Quellensymbolfolge $\rm B$ führen beide Codes zum gleichen Codersignal. Es ergibt sich jeweils ebenfalls ein Einzelimpuls.
- Bei der Dauer–Eins–Folge $\rm A$ ergibt sich nun die Coderfolge $\langle c_\nu \rangle = \langle -1, -1, +1, +1, -1, -1, +1, +1, \text{...}\rangle $ statt $\langle c_\nu \rangle = \langle -1, +1, -1, +1, -1, +1, -1, +1, \text{...}\rangle $.
- Der einfache Decodieralgorithmus des AMI–Codes $($die ternäre $0$ wird zur binären $-1$, die ternären $\pm 1$ zur binären $+1)$ lässt sich bei $\rm BIP2$ nicht anwenden.
(11) Betrachten und interpretieren Sie die verschiedenen AKF– und LDS–Grafiken des $\rm BIP2$ im Vergleich zum AMI–Code.
- Bei $\rm AMI$ ist $\varphi_a(\lambda = \pm 1) = -0.25, \ \varphi_a(\lambda = \pm 2) = 0$. Für $\rm BIP2$ gilt $\varphi_a(\lambda = \pm 1) = 0, \ \varphi_a(\lambda = \pm 2) = -0.25$. In beiden Fällen ist $\varphi_a(\lambda = 0) = 0.5$.
- Aus dem $\rm AMI$–LDS ${\it \Phi}_a(f) = \sin^2 (\pi \cdot f T)$ folgt das $\rm BIP2$–LDS ${\it \Phi}_a(f) = \sin^2 (2\pi \cdot f T)$ durch Stauchung hinsichtlich $f$–Achse.
- Nullstelle bei $f=0$: Es folgen höchstens zwei $+1$ direkt aufeinander, und auch maximal nur zwei $-1$. Beim AMI–Code treten $+1$ und $-1$ nur isoliert auf.
- Nächste Nullstelle bei $f=1/(2T)$: Die unendlich lange $(+1, -1)$–Folge ist bei diesem Code ebenso wie beim Duobinärcode ausgeschlossen.
- Betrachten und interpretieren Sie auch die Funktionen $\varphi_s(\tau)$ und ${\it \Phi}_s(f)$ für die Impulse „Rechteck”, „Nyquist” und „Wurzel–Nyquist”.
Zur Handhabung des Applets
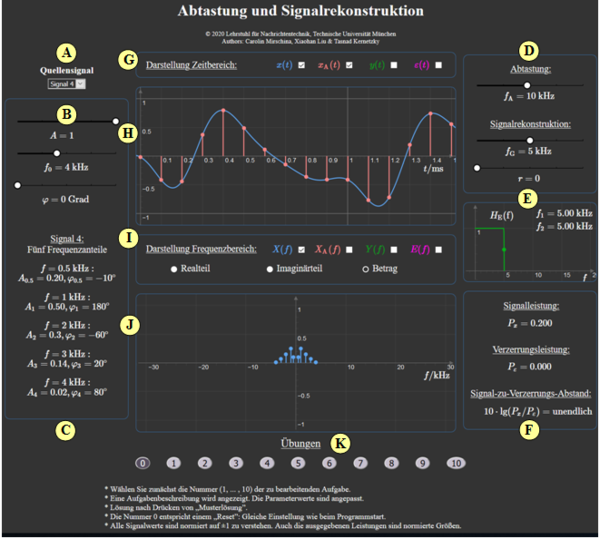
(A) Auswahl eines von vier Quellensignalen
(B) Parameterwahl für Quellensignal $1$ (Amplitude, Frequenz, Phase)
(C) Ausgabe der verwendeten Programmparameter
(D) Parameterwahl für Abtastung $(f_{\rm G})$ und
Signalrekonstruktion $(f_{\rm A},\ r)$
(E) Skizze des Empfänger–Frequenzgangs $H_{\rm E}(f)$
(F) Numerische Ausgabe $(P_x, \ P_{\rm \varepsilon}, \ 10 \cdot \lg(P_x/ P_{\rm \varepsilon})$
(G) Darstellungsauswahl für Zeitbereich
(H) Grafikbereich für Zeitbereich
( I ) Darstellungsauswahl für Frequenzbereich
(J) Grafikbereich für Frequenzbereich
(K) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2010 von Stefan Müller im Rahmen seiner Diplomarbeit (LB) mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch die Exzellenzinitiative der TU München finanziell unterstützt. Wir bedanken uns.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
- ↑ Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.