Modulationsverfahren/Quadratur–Amplitudenmodulation: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Digitale Modulationsverfahren |Vorherige Seite=Lineare digitale Modulationsverfahren |Nächste Seite=Nichtlineare Modulationsverfahren }…“) |
|||
| Zeile 17: | Zeile 17: | ||
*Ist $b$ geradzahlig und die Signalraumzuordnung quadratisch, so können die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einen von $M = 2^{b/2}$ Amplitudenwerten mit gleicher Wahrscheinlichkeit annehmen. Man spricht dann von Quadratur–Amplitudenmodulation (QAM). | *Ist $b$ geradzahlig und die Signalraumzuordnung quadratisch, so können die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einen von $M = 2^{b/2}$ Amplitudenwerten mit gleicher Wahrscheinlichkeit annehmen. Man spricht dann von Quadratur–Amplitudenmodulation (QAM). | ||
*Das in der Grafik betrachtete Beispiel gilt für die 16–QAM mit $b = M =$ 4 und dementsprechend 16 Signalraumpunkten. Bei einer 256–QAM würde $b =$ 8 und $M =$ 16 gelten $(2^b = M^2 =$ 256). | *Das in der Grafik betrachtete Beispiel gilt für die 16–QAM mit $b = M =$ 4 und dementsprechend 16 Signalraumpunkten. Bei einer 256–QAM würde $b =$ 8 und $M =$ 16 gelten $(2^b = M^2 =$ 256). | ||
| + | |||
| + | ==Allgemeine Beschreibung und Signalraumzuordnung (2)== | ||
| + | [[Datei: P_ID1707__Mod_T_4_3_S1_Ganz_neu.png | Blockschaltbild eines linearen Modulators mit I– und Q–Komponente; Signalraumzuordnung 16-QAM]] | ||
| + | |||
| + | |||
| + | '''Fortsetzung der Bildbeschreibung zur obigen Grafik:''' | ||
| + | *Anschließend werden die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einem Diracpuls als Impulsgewichte eingeprägt. Nach der Impulsformung mit dem Sendegrundimpuls $g_s(t)$ gilt somit in den beiden Zweigen des Blockschaltbildes: | ||
| + | $$\begin{align*}s_{\rm I}(t) & = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\\s_{\rm Q}(t) & = \sum_{\nu = - \infty}^{+\infty}a_{\rm | ||
| + | Q\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.\end{align*}$$ | ||
| + | *Anzumerken ist, dass wegen der redundanzfreien Umsetzung die Symboldauer $T$ dieser Signale um den Faktor $b$ größer ist als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Im gezeichneten Beispiel (16-QAM) gilt $T = 4 · T_{\rm B}$. | ||
| + | *Das QAM–Sendesignal $s(t)$ ist dann die Summe der beiden mit Cosinus bzw. Minus–Sinus multiplizierten Teilsignale: | ||
| + | $$\begin{align*}s_{\rm cos}(t) & = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t),\\ s_{\rm -sin}(t) & = -s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t)\end{align*}$$ | ||
| + | *Die beiden Übertragungszweige (I, Q) können als zwei völlig getrennte $M$–stufige ASK–Systeme aufgefasst werden, die sich gegenseitig nicht stören, solange alle Komponenten optimal ausgelegt sind. Die Quadratur–Amplitudenmodulation ermöglicht somit (im Idealfall) eine Verdoppelung der Datenrate bei gleichbleibender Qualität. | ||
Version vom 24. Juni 2016, 09:40 Uhr
Allgemeine Beschreibung und Signalraumzuordnung (1)
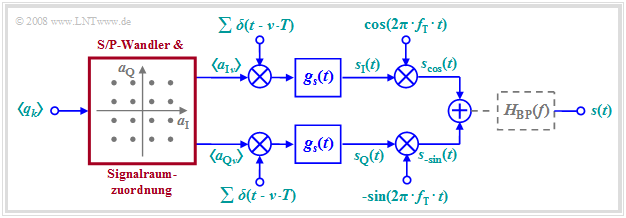
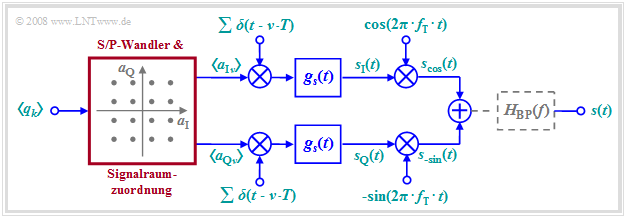
Aufgrund der Orthogonalität von Cosinus und (Minus–)Sinus kann man über einen Übertragungskanal zwei Datenströme unabhängig voneinander übertragen. Die Grafik zeigt das allgemeine Blockschaltbild.
Dieses sehr allgemeine Modell lässt sich wie folgt beschreiben:
- Am Eingang liegt die binäre Quellensymbolfolge $〈q_k〉$ mit der Bitrate $R_{\rm B}$ an. Der zeitliche Abstand zweier Symbole ist damit $T_{\rm B} = 1/R_{\rm B}$.
- Aus jeweils $b$ binären Eingangssymbolen $q_k$ werden zwei mehrstufige Amplitudenkoeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ abgeleitet, wobei „I” für Inphase und „Q” für Quadraturkomponente steht.
- Ist $b$ geradzahlig und die Signalraumzuordnung quadratisch, so können die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einen von $M = 2^{b/2}$ Amplitudenwerten mit gleicher Wahrscheinlichkeit annehmen. Man spricht dann von Quadratur–Amplitudenmodulation (QAM).
- Das in der Grafik betrachtete Beispiel gilt für die 16–QAM mit $b = M =$ 4 und dementsprechend 16 Signalraumpunkten. Bei einer 256–QAM würde $b =$ 8 und $M =$ 16 gelten $(2^b = M^2 =$ 256).
Allgemeine Beschreibung und Signalraumzuordnung (2)
Fortsetzung der Bildbeschreibung zur obigen Grafik:
- Anschließend werden die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einem Diracpuls als Impulsgewichte eingeprägt. Nach der Impulsformung mit dem Sendegrundimpuls $g_s(t)$ gilt somit in den beiden Zweigen des Blockschaltbildes:
$$\begin{align*}s_{\rm I}(t) & = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\\s_{\rm Q}(t) & = \sum_{\nu = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.\end{align*}$$
- Anzumerken ist, dass wegen der redundanzfreien Umsetzung die Symboldauer $T$ dieser Signale um den Faktor $b$ größer ist als die Bitdauer $T_{\rm B}$ des binären Quellensignals. Im gezeichneten Beispiel (16-QAM) gilt $T = 4 · T_{\rm B}$.
- Das QAM–Sendesignal $s(t)$ ist dann die Summe der beiden mit Cosinus bzw. Minus–Sinus multiplizierten Teilsignale:
$$\begin{align*}s_{\rm cos}(t) & = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t),\\ s_{\rm -sin}(t) & = -s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t)\end{align*}$$
- Die beiden Übertragungszweige (I, Q) können als zwei völlig getrennte $M$–stufige ASK–Systeme aufgefasst werden, die sich gegenseitig nicht stören, solange alle Komponenten optimal ausgelegt sind. Die Quadratur–Amplitudenmodulation ermöglicht somit (im Idealfall) eine Verdoppelung der Datenrate bei gleichbleibender Qualität.