Aufgaben:Aufgabe 4.4: Zum Quantisierungsrauschen: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Pulscodemodulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1616__Mod_A_4_4.png|right|]] |
| + | Zur Berechnung der Quantisierungsrauschleistung $P_Q$ gehen wir von einem periodischen sägezahnförmigen Quellensignal $q(t)$ mit dem Wertebereich $±q_{max}$ und der Periodendauer $T_0$ aus. | ||
| + | |||
| + | Im mittleren Zeitbereich $–T_0/2 ≤ t ≤ T_0/2$ gilt: | ||
| + | $$q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$$ | ||
| + | Dessen Leistung wird hier mit $P_S$ bezeichnet. | ||
| + | |||
| + | Dieses Signal wird entsprechend der Grafik mit $M = 6$ Stufen quantisiert. Der lineare Quantisierer ist für den Amplitudenbereich $±Q_{max}$ ausgelegt, so dass jedes Quantisierungsintervall die Breite $Δ = 2/M · Q_{max}$ aufweist. Die Grafik zeigt diesen Sachverhalt für $Q_{max} = q_{max} = 6 V$. Von diesen Zahlenwerten soll bis einschließlich Teilaufgabe e) ausgegangen werden. | ||
| + | |||
| + | Die so genannte '''Quantisierungsrauschleistung''' ist als der quadratische Mittelwert des Differenzsignals $ε(t) = q_Q(t) – q(t)$ definiert. Es gilt | ||
| + | $$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$ | ||
| + | wobei die Zeit $T_0'$ geeignet zu wählen ist. Als Quantisierungs–SNR bezeichnet man das Verhältnis | ||
| + | $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}}\hspace{0.05cm},$$ | ||
| + | das meist in dB angegeben wird. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf das [http://www.lntwww.de/Modulationsverfahren/Pulscodemodulation Kapitel 4.1]. | ||
| + | |||
| Zeile 9: | Zeile 25: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Berechnen Sie die Signalleistung $P_S$ (auf 1 Ω bezogen): |
| − | |type=" | + | |type="{}"} |
| − | - | + | $P_S$ = { 12 3% } $V^2$ |
| − | + | + | |
| + | {Welche Aussagen treffen für das Fehlersignal $ε(t)$ zu? | ||
| + | |type="{}"} | ||
| + | + $ε(t)$ hat einen sägezahnförmigen Verlauf. | ||
| + | - $ε(t)$ hat einen stufenförmigen Verlauf. | ||
| + | + $ε(t)$ ist auf den Bereich $±Δ/2 = ±1V$ beschränkt. | ||
| + | + $ε(t)$ besitzt die Periodendauer $T_0' = T_0/M$. | ||
| + | |||
| + | |||
| + | {Wie groß ist die Quantisierungsrauschleistung? | ||
| + | |type="{}"} | ||
| + | $M=6 P_Q$ = { 0.333 3% } $V^2$ | ||
| + | {Berechnen Sie den Quantisierungsrauschabstand für $M = 6$. | ||
| + | |type="{}"} | ||
| + | $M = 6: 10 · lg ρ_Q$ = { 15.56 3% } $dB$ | ||
| − | { | + | {Welche Werte ergeben sich bei Quantisierung mit $N = 8$ bzw. $N = 16 Bit$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ N = 8: 10 · lg ρ_Q$ = { 48.16 3% } $dB$ |
| + | $ N = 16: 10 · lg ρ_Q$ = { 96.32 3% } $dB$ | ||
| + | {Welche Voraussetzungen müssen erfüllt sein, damit die abgeleitete Gleichung für $ρ_Q$ angewandt werden kann? | ||
| + | |type="[]"} | ||
| + | + Alle Amplitudenwerte sind gleichwahrscheinlich. | ||
| + | + Es liegt ein linearer Quantisierer vor. | ||
| + | + Der Quantisierer ist genau an das Signal angepasst ($Q_{max} = q_{max}$). | ||
| Zeile 25: | Zeile 61: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Die Signalleistung $P_S$ ist gleich dem quadratischen Mittelwert von $q(t)$, wenn der Bezugswiderstand 1Ω verwendet und dementsprechend für die Leistung die Einheit „$V^2$” in Kauf genommen wird. Aufgrund der Periodizität und der Symmetrie genügt die Mittelung über $T_0/2$: |
| − | '''2.''' | + | $$P_{\rm S} = \frac{1}{T_0/2} \cdot \int\limits_{0}^{T_0/2}q^2(t) \hspace{0.05cm}{\rm d}t = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \int\limits_{0}^{T_0/2}\left ( { 2 \cdot t}/{T_0} \right )^2 \hspace{0.05cm}{\rm d}t=$$ $$ = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \frac{T_0}{2} \cdot \int\limits_{0}^{1}x^2 \hspace{0.05cm}{\rm d}x = \frac{q_{\rm max}^2}{3} \hspace{0.05cm}.$$ |
| + | Hierbei wurde die Substitution $x = 2 · t/T_0$ verwendet. Mit $q_{max} = 6 V$ erhält man $P_S = 12 V^2$. | ||
| + | |||
| + | '''2.''' Wir gehen hier von $Q_{max} = q_{max} = 6 V$ aus. Damit ergibt sich das sägezahnförmige Fehlersignal $ε(t)$ zwischen $±1V$ und der Periodendauer $T0' = T_0/6$. | ||
| + | [[Datei:P_ID1616__Mod_A_4_4.png]] | ||
| + | |||
| + | Richtig sind also die Lösungsvorschläge 1, 3 und.4. | ||
'''3.''' | '''3.''' | ||
'''4.''' | '''4.''' | ||
Version vom 4. Januar 2017, 17:01 Uhr
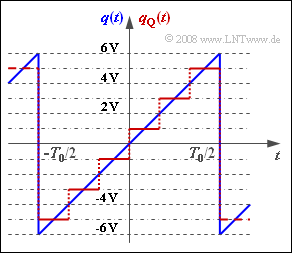
Zur Berechnung der Quantisierungsrauschleistung $P_Q$ gehen wir von einem periodischen sägezahnförmigen Quellensignal $q(t)$ mit dem Wertebereich $±q_{max}$ und der Periodendauer $T_0$ aus.
Im mittleren Zeitbereich $–T_0/2 ≤ t ≤ T_0/2$ gilt: $$q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$$ Dessen Leistung wird hier mit $P_S$ bezeichnet.
Dieses Signal wird entsprechend der Grafik mit $M = 6$ Stufen quantisiert. Der lineare Quantisierer ist für den Amplitudenbereich $±Q_{max}$ ausgelegt, so dass jedes Quantisierungsintervall die Breite $Δ = 2/M · Q_{max}$ aufweist. Die Grafik zeigt diesen Sachverhalt für $Q_{max} = q_{max} = 6 V$. Von diesen Zahlenwerten soll bis einschließlich Teilaufgabe e) ausgegangen werden.
Die so genannte Quantisierungsrauschleistung ist als der quadratische Mittelwert des Differenzsignals $ε(t) = q_Q(t) – q(t)$ definiert. Es gilt $$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$ wobei die Zeit $T_0'$ geeignet zu wählen ist. Als Quantisierungs–SNR bezeichnet man das Verhältnis $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}}\hspace{0.05cm},$$ das meist in dB angegeben wird.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1.
Fragebogen
Musterlösung
2. Wir gehen hier von $Q_{max} = q_{max} = 6 V$ aus. Damit ergibt sich das sägezahnförmige Fehlersignal $ε(t)$ zwischen $±1V$ und der Periodendauer $T0' = T_0/6$.
Richtig sind also die Lösungsvorschläge 1, 3 und.4. 3. 4. 5. 6. 7.