Aufgaben:Aufgabe 4.4: Zum Quantisierungsrauschen

• Zurück zum Buch

Zur Berechnung der Quantisierungsrauschleistung $P_Q$ gehen wir von einem periodischen sägezahnförmigen Quellensignal $q(t)$ mit dem Wertebereich $±q_{max}$ und der Periodendauer $T_0$ aus.

Im mittleren Zeitbereich $–T_0/2 ≤ t ≤ T_0/2$ gilt: $$q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$$ Dessen Leistung wird hier mit $P_S$ bezeichnet.

Dieses Signal wird entsprechend der Grafik mit $M = 6$ Stufen quantisiert. Der lineare Quantisierer ist für den Amplitudenbereich $±Q_{max}$ ausgelegt, so dass jedes Quantisierungsintervall die Breite $Δ = 2/M · Q_{max}$ aufweist. Die Grafik zeigt diesen Sachverhalt für $Q_{max} = q_{max} = 6 V$. Von diesen Zahlenwerten soll bis einschließlich Teilaufgabe e) ausgegangen werden.

Die so genannte Quantisierungsrauschleistung ist als der quadratische Mittelwert des Differenzsignals $ε(t) = q_Q(t) – q(t)$ definiert. Es gilt $$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$ wobei die Zeit $T_0'$ geeignet zu wählen ist. Als Quantisierungs–SNR bezeichnet man das Verhältnis $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}}\hspace{0.05cm},$$ das meist in dB angegeben wird.

Hinweise:

• Die Aufgabe gehört zum Kapitel Pulscodemodulation.
• Bezug genommen wird insbesondere auf die Seiten Natürliche und diskrete Abtastung.
• Das abgetastete Quellensignal wird mit $q_{\rm A}(t)$ bezeichnet und dessen Spektralfunktion mit $Q_{\rm A}(f)$. Die Abtastung erfolgt stets bei $ν · T_{\rm A}$.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1.

Fragebogen

1

Berechnen Sie die Signalleistung $P_S$ (auf 1 Ω bezogen):

$P_S$ = $V^2$

2

Welche Aussagen treffen für das Fehlersignal $ε(t)$ zu?

+ $ε(t)$ hat einen sägezahnförmigen Verlauf.

- $ε(t)$ hat einen stufenförmigen Verlauf.

+ $ε(t)$ ist auf den Bereich $±Δ/2 = ±1V$ beschränkt.

+ $ε(t)$ besitzt die Periodendauer $T_0' = T_0/M$.

3

Wie groß ist die Quantisierungsrauschleistung?

$M=6 P_Q$ = $V^2$

4

Berechnen Sie den Quantisierungsrauschabstand für $M = 6$.

$M = 6: 10 · lg ρ_Q$ = $dB$

5

Welche Werte ergeben sich bei Quantisierung mit $N = 8$ bzw. $N = 16 Bit$?

$ N = 8: 10 · lg ρ_Q$ = $dB$

$ N = 16: 10 · lg ρ_Q$ = $dB$

6

Welche Voraussetzungen müssen erfüllt sein, damit die abgeleitete Gleichung für $ρ_Q$ angewandt werden kann?

	Alle Amplitudenwerte sind gleichwahrscheinlich.
	Es liegt ein linearer Quantisierer vor.
	Der Quantisierer ist genau an das Signal angepasst ($Q_{max} = q_{max}$).

Musterlösung

Musterlösung

1. Die Signalleistung $P_S$ ist gleich dem quadratischen Mittelwert von $q(t)$, wenn der Bezugswiderstand 1Ω verwendet und dementsprechend für die Leistung die Einheit „$V^2$” in Kauf genommen wird. Aufgrund der Periodizität und der Symmetrie genügt die Mittelung über $T_0/2$: $$P_{\rm S} = \frac{1}{T_0/2} \cdot \int\limits_{0}^{T_0/2}q^2(t) \hspace{0.05cm}{\rm d}t = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \int\limits_{0}^{T_0/2}\left ( { 2 \cdot t}/{T_0} \right )^2 \hspace{0.05cm}{\rm d}t=$$ $$ = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \frac{T_0}{2} \cdot \int\limits_{0}^{1}x^2 \hspace{0.05cm}{\rm d}x = \frac{q_{\rm max}^2}{3} \hspace{0.05cm}.$$ Hierbei wurde die Substitution $x = 2 · t/T_0$ verwendet. Mit $q_{max} = 6 V$ erhält man $P_S = 12 V^2$.

2. Wir gehen hier von $Q_{max} = q_{max} = 6 V$ aus. Damit ergibt sich das sägezahnförmige Fehlersignal $ε(t)$ zwischen $±1V$ und der Periodendauer $T0' = T_0/6$.

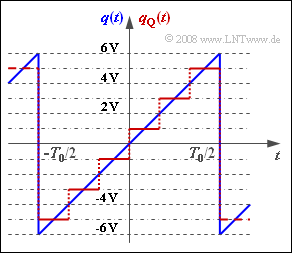
Richtig sind also die Lösungsvorschläge 1, 3 und.4.

3. Das Fehlersignal $ε(t)$ verläuft ebenso wie $q(t)$ sägezahnförmig. Somit eignet sich zur Berechnung des quadratischen Mittelwertes dieselbe Gleichung wie in Teilaufgabe a). Zu beachten ist die um den Faktor M kleinere Amplitude, während die unterschiedliche Periodendauer für die Mittelung keine Rolle spielt: $$P_{\rm Q} = \frac{P_{\rm S}}{M^2} = \frac{12\,{\rm V}^2}{36}\hspace{0.15cm}\underline {= 0.333\,{\rm V}^2 }\hspace{0.05cm}.$$

4. Die Ergebnisse der Teilaufgaben a) und c) führen zum Quantisierungs–SNR: $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}} = M^2 = 36 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q}\hspace{0.15cm}\underline { =15.56\,{\rm dB}} \hspace{0.05cm}.$$

5. Mit $M = 2^N$ erhält man allgemein: $$ \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} =20 \cdot {\rm lg}\hspace{0.1cm}(2)\cdot N \hspace{0.15cm}\underline {\approx 6.02\,{\rm dB}} \cdot N .$$ Daraus ergeben sich die gesuchten Sonderfälle: $$N = 8:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline {= 48.16\,{\rm dB}}\hspace{0.05cm},$$ $$N = 16:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline { = 96.32\,{\rm dB}}\hspace{0.05cm}.$$

6. Alle diese Voraussetzungen müssen erfüllt sein. Bei nichtlinearer Quantisierung gilt $ρ_Q = M^2$ nicht. Bei einer anderen Amplitudenverteilung als der Gleichverteilung ist $ρ_Q = M^2$ ebenfalls nur eine Näherung, die jedoch meist in Kauf genommen wird. Ist $Q_{max} < q_{max}$, so kommt es zu einem unzulässigen Abschneiden der Spitzen, während mit $Q_{max} > q_{max}$ die Quantisierungsintervalle größer sind als erforderlich.

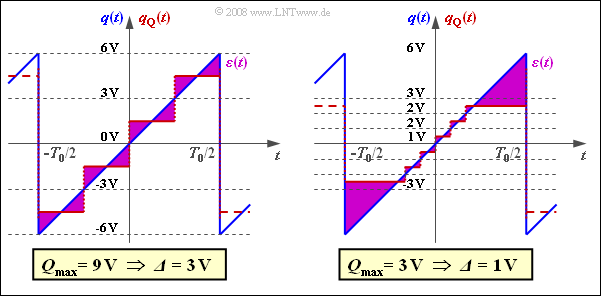
Die Grafik zeigt die Fehlersignale $ε(t)$ für $Q_{max} > q_{max}$ (links) und $Q_{max} < q_{max}$ (rechts). In beiden Fällen ergibt sich eine deutlich größere Quantisierungsrauschleistung als unter Punkt c) berechnet.