Aufgaben:Aufgabe 4.5: Nichtlineare Quantisierung: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Pulscodemodulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1620__Mod_A_4_5.png|right|]] |
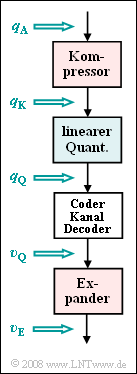
| + | Zur Untersuchung der nichtlinearen Quantisierung gehen wir vom skizzierten Systemmodell aus, wobei wir den Einfluss des Kanals und der PCM–Codierung bzw. –Decodierung außer Acht lassen. Somit gilt stets $υ_Q(ν · T_A) = q_Q(ν · T_A)$, wobei im Weiteren auf die Zeitangabe $ν · T_A$ verzichtet wird. | ||
| + | |||
| + | Durch den Vergleich von jeweils einer Ausgangsgröße mit einer Eingangsgröße kann man den Einfluss | ||
| + | :* des Kompressors ⇒ $q_K(q_A)$, | ||
| + | :* des linearen Quantisierers ⇒ $q_Q(q_K)$, | ||
| + | :* des nichtlinearen Quantisierers ⇒ $q_Q(q_A)$, | ||
| + | :* des Expanders ⇒ $υ_E(υ_Q)$ sowie | ||
| + | :* des Gesamtsystems ⇒ $υ_E(q_A)$ | ||
| + | |||
| + | analysieren. Dabei wird von folgenden Voraussetzungen ausgegangen: | ||
| + | |||
| + | :* Alle Abtastwerte $q_A$ liegen im Wertebereich $±1$ vor. | ||
| + | :* Der (lineare) Quantisierer arbeitet mit $M = 256$ Quantisierungsstufen, die mit $μ = 0$ bis $μ = 255$ gekennzeichnet werden. | ||
| + | :* Zur Kompression wird die sogenannte 13–Segment–Kennlinie verwendet. | ||
| + | |||
| + | Im Bereich $|q_A| ≤ 1/64$ gilt $q_K = q_A$. Für $q_A > 1/64$ ergeben sich mit k = 1, ... , 6 folgende sechs weitere Bereiche der Kompressorkennlinie: | ||
| + | $$q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + \frac{k}{8}\hspace{0.3cm} {\rm im\,\,Bereich}\hspace{0.3cm}2^{k-7}< q_{\rm A} \le 2^{k-6} \hspace{0.05cm}.$$ | ||
| + | Weitere sechs Bereiche gibt es für die negativen $q_A$–Werte mit k = –1, ... , –6, die punktsymmetrisch zum Ursprung liegen. Diese werden in dieser Aufgabe jedoch nicht weiter betrachtet. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf das [http://www.lntwww.de/Modulationsverfahren/Pulscodemodulation Kapitel 4.1]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Zeile 9: | Zeile 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Es gelte $q_A = 0.4$. Welchen Ausgangswert qK liefert der Kompressor? |
| − | |type=" | + | |type="{}"} |
| − | + | $q_A = 0.4: q_K$ = ,{ 0.825 3% } | |
| − | + | ||
| + | |||
| + | {Zu welchem Quantisierungsintervall $μ$ gehört $q_A = 0.4$? | ||
| + | |type="{}"} | ||
| + | $q_A = 0.4: μ$ = { 233 3% } | ||
| + | {Welcher Quantisierungswert $q_Q$ gehört zu $q_A = 0.4$? | ||
| + | |type="{}"} | ||
| + | $q_A = 0.4: q_Q$ ={ 0.824 3% } | ||
| − | { | + | {Welcher Quantisierungswert $q_Q$ gehört dagegen zu $q_A = 0.04$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $q_A = 0.04: q_Q$ = { 0.41 3% } |
| + | {Beim Empfänger liegt der Eingangswert $υ_Q = 211/256 ≈ 0.824$ an. Welchen Wert $υ_E$ liefert der Expander? | ||
| + | |type="{}"} | ||
| + | $υ_Q = 211/256: υ_E$ = { 0.398 3% } | ||
| + | {Welche Eigenschaften weist die Kennlinie $q_Q(q_A)$ auf? | ||
| + | |type="[]"} | ||
| + | + $q_Q(q_A)$ approximiert die Kompressorkennlinie in Stufen. | ||
| + | - $q_Q(q_A)$ approximiert die Winkelhalbierende in Stufen. | ||
| + | - Die Stufenbreite ist in allen Segmenten (außer k = 0) gleich groß. | ||
| + | + Die Stufenhöhe ist in allen Segmenten (außer k = 0) gleich groß. | ||
| + | {Welche Eigenschaften weist die Kennlinie $υ_E(q_A)$ auf? | ||
| + | |type="[]"} | ||
| + | - $υ_E(q_A)$ approximiert die Kompressorkennlinie in Stufen. | ||
| + | + $υ_E(q_A)$ approximiert die Winkelhalbierende in Stufen. | ||
| + | - Die Stufenbreite ist in allen Segmenten (außer k = 0) gleich groß. | ||
| + | - Die Stufenhöhe ist in allen Segmenten (außer k = 0) gleich groß. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Der Abtastwert $q_A = 0.4$ gehört zum Segment k = 5, das den Bereich $1/4 < q_A ≤ 1/2$ abdeckt. Aus der angegebenen Gleichung folgt daraus mit k = 5: |
| − | '''2.''' | + | $$q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + \frac{k}{8}= \frac{1}{2}\cdot 0.4 + \frac{5}{8} \hspace{0.15cm}\underline {= 0.825}\hspace{0.05cm}.$$ |
| − | '''3.''' | + | |
| − | '''4.''' | + | '''2.''' Der Eingangswert des linearen Quantisierers ist nun $q_K = 0.825$, so dass folgende Rechnung zutrifft: |
| − | '''5.''' | + | $$\frac{105}{128} < q_{\rm K} = 0.825 \le \frac{106}{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 105 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 105\hspace{0.15cm}\underline { = 233} \hspace{0.05cm}.$$ |
| − | '''6.''' | + | |
| − | '''7.''' | + | '''3.'''Entsprechend der Angabenseite wird das Quantisierungsintervall $μ = 128 + m$ durch den Wert |
| + | $q_Q = 1/256 + m/128$ repräsentiert. Mit $m = 105$ folgt daraus: | ||
| + | $$q_{\rm Q} = \frac{1}{256} + \frac{105}{128} \hspace{0.15cm}\underline {\approx 0.824} \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''4.''' Entsprechend der obigen Musterlösung gilt mit dem Eingangswert $q_A = 0.04$: | ||
| + | $$ \frac{1}{32} < q_{\rm A} \le \frac{1}{16}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} k = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} q_{\rm K} = 2^2 \cdot 0.04 + \frac{2}{8}= 0.41$$ | ||
| + | $$\Rightarrow \hspace{0.3cm}\frac{52}{128} < q_{\rm K} = 0.41 \le \frac{53}{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 52 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 52 = 180$$ | ||
| + | $$\Rightarrow \hspace{0.3cm}q_{\rm Q} = \frac{1}{256} + \frac{52}{128} \hspace{0.15cm}\underline {= 0.41} \hspace{0.05cm}.$$ | ||
| + | |||
| + | [[Datei:P_ID1621__Mod_A_4_5e.png|right|]] | ||
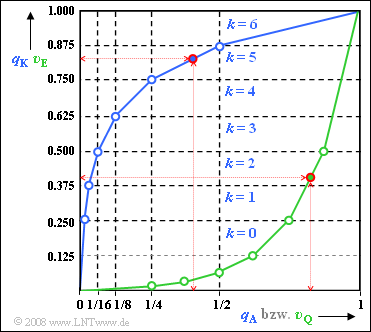
| + | '''5.''' Beim Kompressor hat $q_A = 0.4$ zum Ausgangswert $q_K = 0.825$ geführt und nach der Quantisierung zum Wert 0.824 (siehe Teilaufgaben a und c). Die Grafik zeigt, dass sich damit empfängerseitig aus $υ_Q = 0.824$ näherungsweise wieder der Wert $υ_E ≈ 0.4$ ergibt. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Aufgrund der Quantisierung ist dies jedoch nur eine Näherung. Exakt gilt: | ||
| + | $$ v_{\rm E} = 0.25 + \frac{0.824-0.750}{0.875-0.750} \cdot 0.25 \hspace{0.15cm}\underline {= 0.398} \hspace{0.05cm}.$$ | ||
| + | Dieser Rechengang ist anhand der Grafik nachvollziehbar. Obwohl die Expanderkennlinie $υ_E(υ_Q)$ gleich der Umkehrfunktion der Kompressorkennlinie $q_K(q_A)$ ist, ergibt sich ein Fehler, da die Eingangsgröße $υ_Q$ des Expanders wertdiskret ist (Einfluss der Quantisierung). | ||
| + | |||
| + | |||
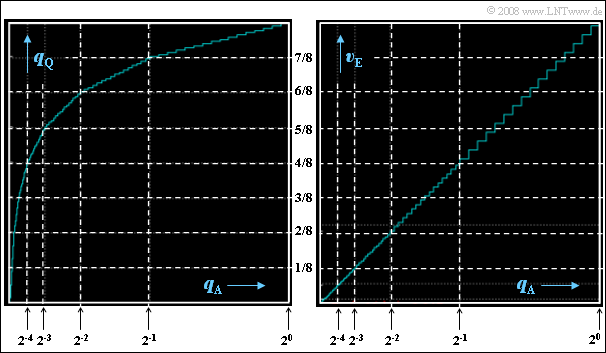
| + | '''6.''' Richtig sind die Aussagen 1 und 4, wie anhand der linken Grafik nachgeprüft werden kann. Die Breite der einzelnen Stufen ist in jedem Segment unterschiedlich. Im äußersten Segment (k = 6) beträgt diese 0.5/16 = 1/32, im nächsten Segment (k = 5) nur mehr 0.25/16 = 1/64. Die Stufenbreiten in den weiteren Segmenten sind 1/128 (k = 4), 1/256 (k = 3), 1/512 (k = 2) und 1/1024 (k = 1). Der innerste Bereich von –1/64 bis +1/64 wird in 64 Stufen unterteilt, woraus sich die Stufenbreite 1/2048 ergibt. | ||
| + | [[Datei:P_ID1622__Mod_A_4_5f.png]] | ||
| + | |||
| + | Die Stufenhöhe ist dagegen in den Segmenten k ≠ 0 konstant gleich 1/8 geteilt durch 16 = 1/128 und im mittleren Segment gleich 1/256. | ||
| + | |||
| + | |||
| + | '''7.''' Richtig ist hier nur die zweite Aussage. Durch den Expander verläuft die Quantisierung nun entlang der Winkelhalbierenden. In jedem Segment sind Stufenbreite und Stufenhöhe konstant. Wie die rechte Grafik zeigt, sind aber im nächstinneren Segment die Breite und die Höhe nur mehr halb so groß. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 4. Januar 2017, 18:05 Uhr
Zur Untersuchung der nichtlinearen Quantisierung gehen wir vom skizzierten Systemmodell aus, wobei wir den Einfluss des Kanals und der PCM–Codierung bzw. –Decodierung außer Acht lassen. Somit gilt stets $υ_Q(ν · T_A) = q_Q(ν · T_A)$, wobei im Weiteren auf die Zeitangabe $ν · T_A$ verzichtet wird.
Durch den Vergleich von jeweils einer Ausgangsgröße mit einer Eingangsgröße kann man den Einfluss
- des Kompressors ⇒ $q_K(q_A)$,
- des linearen Quantisierers ⇒ $q_Q(q_K)$,
- des nichtlinearen Quantisierers ⇒ $q_Q(q_A)$,
- des Expanders ⇒ $υ_E(υ_Q)$ sowie
- des Gesamtsystems ⇒ $υ_E(q_A)$
analysieren. Dabei wird von folgenden Voraussetzungen ausgegangen:
- Alle Abtastwerte $q_A$ liegen im Wertebereich $±1$ vor.
- Der (lineare) Quantisierer arbeitet mit $M = 256$ Quantisierungsstufen, die mit $μ = 0$ bis $μ = 255$ gekennzeichnet werden.
- Zur Kompression wird die sogenannte 13–Segment–Kennlinie verwendet.
Im Bereich $|q_A| ≤ 1/64$ gilt $q_K = q_A$. Für $q_A > 1/64$ ergeben sich mit k = 1, ... , 6 folgende sechs weitere Bereiche der Kompressorkennlinie: $$q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + \frac{k}{8}\hspace{0.3cm} {\rm im\,\,Bereich}\hspace{0.3cm}2^{k-7}< q_{\rm A} \le 2^{k-6} \hspace{0.05cm}.$$ Weitere sechs Bereiche gibt es für die negativen $q_A$–Werte mit k = –1, ... , –6, die punktsymmetrisch zum Ursprung liegen. Diese werden in dieser Aufgabe jedoch nicht weiter betrachtet.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1.
Fragebogen
Musterlösung
2. Der Eingangswert des linearen Quantisierers ist nun $q_K = 0.825$, so dass folgende Rechnung zutrifft: $$\frac{105}{128} < q_{\rm K} = 0.825 \le \frac{106}{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 105 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 105\hspace{0.15cm}\underline { = 233} \hspace{0.05cm}.$$
3.Entsprechend der Angabenseite wird das Quantisierungsintervall $μ = 128 + m$ durch den Wert $q_Q = 1/256 + m/128$ repräsentiert. Mit $m = 105$ folgt daraus: $$q_{\rm Q} = \frac{1}{256} + \frac{105}{128} \hspace{0.15cm}\underline {\approx 0.824} \hspace{0.05cm}.$$
4. Entsprechend der obigen Musterlösung gilt mit dem Eingangswert $q_A = 0.04$: $$ \frac{1}{32} < q_{\rm A} \le \frac{1}{16}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} k = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} q_{\rm K} = 2^2 \cdot 0.04 + \frac{2}{8}= 0.41$$ $$\Rightarrow \hspace{0.3cm}\frac{52}{128} < q_{\rm K} = 0.41 \le \frac{53}{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 52 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 52 = 180$$ $$\Rightarrow \hspace{0.3cm}q_{\rm Q} = \frac{1}{256} + \frac{52}{128} \hspace{0.15cm}\underline {= 0.41} \hspace{0.05cm}.$$
5. Beim Kompressor hat $q_A = 0.4$ zum Ausgangswert $q_K = 0.825$ geführt und nach der Quantisierung zum Wert 0.824 (siehe Teilaufgaben a und c). Die Grafik zeigt, dass sich damit empfängerseitig aus $υ_Q = 0.824$ näherungsweise wieder der Wert $υ_E ≈ 0.4$ ergibt.
Aufgrund der Quantisierung ist dies jedoch nur eine Näherung. Exakt gilt: $$ v_{\rm E} = 0.25 + \frac{0.824-0.750}{0.875-0.750} \cdot 0.25 \hspace{0.15cm}\underline {= 0.398} \hspace{0.05cm}.$$ Dieser Rechengang ist anhand der Grafik nachvollziehbar. Obwohl die Expanderkennlinie $υ_E(υ_Q)$ gleich der Umkehrfunktion der Kompressorkennlinie $q_K(q_A)$ ist, ergibt sich ein Fehler, da die Eingangsgröße $υ_Q$ des Expanders wertdiskret ist (Einfluss der Quantisierung).
6. Richtig sind die Aussagen 1 und 4, wie anhand der linken Grafik nachgeprüft werden kann. Die Breite der einzelnen Stufen ist in jedem Segment unterschiedlich. Im äußersten Segment (k = 6) beträgt diese 0.5/16 = 1/32, im nächsten Segment (k = 5) nur mehr 0.25/16 = 1/64. Die Stufenbreiten in den weiteren Segmenten sind 1/128 (k = 4), 1/256 (k = 3), 1/512 (k = 2) und 1/1024 (k = 1). Der innerste Bereich von –1/64 bis +1/64 wird in 64 Stufen unterteilt, woraus sich die Stufenbreite 1/2048 ergibt.
Die Stufenhöhe ist dagegen in den Segmenten k ≠ 0 konstant gleich 1/8 geteilt durch 16 = 1/128 und im mittleren Segment gleich 1/256.
7. Richtig ist hier nur die zweite Aussage. Durch den Expander verläuft die Quantisierung nun entlang der Winkelhalbierenden. In jedem Segment sind Stufenbreite und Stufenhöhe konstant. Wie die rechte Grafik zeigt, sind aber im nächstinneren Segment die Breite und die Höhe nur mehr halb so groß.