Aufgaben:Aufgabe 4.7: Spektren von ASK und BPSK: Unterschied zwischen den Versionen

Version vom 7. Januar 2017, 16:28 Uhr

Die Sendesignale von ASK (Amplitude Shift Keying) und BPSK (Binary Phase Shift Keying) können beide in der Form $s(t) = q(t) · z(t)$ dargestellt werden, wobei z(t) eine harmonische Schwingung mit der Frequenz $f_T$ und der Amplitude 1 darstellt. Die Trägerphase $ϕ_T$ ist für die hier betrachteten Leistungsdichtespektren nicht von Bedeutung.

Bei ASK sind unipolare Amplitudenkoeffizienten – das heißt: $a_ν ∈ {0, 1}$ – des Quellensignals $$ q(t) = \sum_{\nu = - \infty}^{+\infty}a_\nu \cdot g_q (t - \nu \cdot T)$$ anzusetzen, während im Fall der BPSK $a_ν$ ∈ {–1, +1} zu berücksichtigen ist. Die Quelle ist jeweils redundanzfrei, was bedeutet, dass die beiden möglichen Symbole ±1 gleichwahrscheinlich sind und die Symbole statistisch voneinander unabhängig.

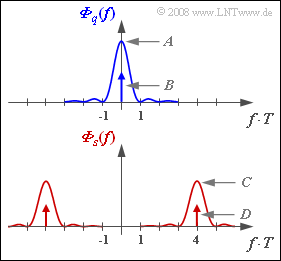
In der Grafik sind die Leistungsdichtespektren $Φ_q(f)$ und $Φ_s(f)$ von Quellensignal und Sendesignal angegeben, die sich bei einem NRZ–Rechteckimpuls $g_q(t)$ mit der Amplitude $s_0 = 2 V$ und der Dauer $T = 1 μs$ ergeben. Damit lautet die Spektralfunktion: $$G_q(f) = s_0 \cdot T \cdot {\rm si}(\pi f T)\hspace{0.05cm}.$$ Zu bestimmen sind in dieser Aufgabe die Konstanten A, B, C und D für ASK und BPSK.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.2 dieses Buches sowie auf das Kapitel 2.1 im Buch „Digitalsignalübertragung”.

Fragebogen

$ASK: A$ =

$10^{-6}$ $V^2$

$B$ =

$V^2$

$ASK: C$ =

$10^{-6}$ $V^2/Hz$

$D$ =

$V^2$

$BPSK: A$ =

$10^{-6}$ $V^2/Hz$

$B$ =

$V^2$

$BPSK: C$ =

$10^{-6}$ $V^2/Hz$

$D$ =

$V^2$

+ Der kontinuierliche Anteil von $Φ_q(f)$ ist formgleich mit $|Gq(f)|^2$.

- $Φ_q(f)$ beinhaltet bei ASK genau eine Diraclinie bei $f = 0$.

- $Φ_q(f)$ beinhaltet bei BPSK genau eine Diraclinie bei $f = 0$.

Musterlösung

1. Der Gleichanteil des unipolaren redundanzfreien Quellensignals beträgt $m_q = s_0/2$. Das Diracgewicht ist somit $B = m_q^2 = s_0^2/4 = 1 V^2$. Ohne diesen Gleichanteil ergibt sich das stochastische Rechtecksignal $q(t) – m_q$ ∈ {$+s_0/2, –s_0/2$}. Dieses gleichsignalfreie Signal besitzt den kontinuierlichen LDS–Anteil $(s_0/2)^2 · T · si^2(πfT)$, woraus der gesuchte Wert bei der Frequenz f = 0 ermittelt werden kann: '"`UNIQ-MathJax34-QINU`"' '''2.''' Das Spektrum Z(f) eines Cosinussignals z(t) besteht aus zwei Diracfunktionen bei ±fT, jeweils mit dem Gewicht 1/2. Das Leistungsdichtespektrum Φz(f) besteht ebenfalls aus den beiden Diracfunktionen, nun aber mit jeweiligem Gewicht 1/4. Die Faltung Φq(f) ∗ Φz(f) ergibt das Leistungsdichtespektrum $\Phi_s(f)$ des Sendesignals. Daraus folgt: $$C = \frac{A}{4} = 0.25 \cdot 10^{-6} V^2/Hz, D = \frac{B}{4} = 0.25 V^2$$

3.

4.

5.

@@ Zeile 49: / Zeile 49: @@
 ===Musterlösung===
 {{ML-Kopf}}
-'''1.''' Der Gleichanteil des unipolaren redundanzfreien Quellensignals beträgt $m_q = s_0/2$. Das Diracgewicht ist somit $B = m_q^2 = s_0^2/4 = 1 V^2$. Ohne diesen Gleichanteil ergibt sich das stochastische Rechtecksignal $q(t) – m_q$ ∈ {$+s_0/2$, $–s_0/2$}. Dieses gleichsignalfreie Signal besitzt den kontinuierlichen LDS–Anteil $(s_0/2)^2 · T · si^2(πfT)$, woraus der gesuchte Wert bei der Frequenz f = 0 ermittelt werden kann:
+'''1.''' Der Gleichanteil des unipolaren redundanzfreien Quellensignals beträgt $m_q = s_0/2$. Das Diracgewicht ist somit $B = m_q^2 = s_0^2/4 = 1 V^2$. Ohne diesen Gleichanteil ergibt sich das stochastische Rechtecksignal $q(t) – m_q$ ∈ {$+s_0/2, –s_0/2$}. Dieses gleichsignalfreie Signal besitzt den kontinuierlichen LDS–Anteil $(s_0/2)^2 · T · si^2(πfT)$, woraus der gesuchte Wert bei der Frequenz f = 0 ermittelt werden kann:
+$$A = \frac{s_0^2 \cdot T}{4} = \frac{(2V)^2 \cdot 10^{-6} s}{4} = 10^{-6} V^2/Hz$$
+'''2.''' Das Spektrum Z(f) eines Cosinussignals z(t) besteht aus zwei Diracfunktionen bei ±fT, jeweils mit dem Gewicht 1/2. Das Leistungsdichtespektrum Φz(f) besteht ebenfalls aus den beiden Diracfunktionen, nun aber mit jeweiligem Gewicht 1/4. Die Faltung Φq(f) ∗ Φz(f) ergibt das Leistungsdichtespektrum $\Phi_s(f)$ des Sendesignals. Daraus folgt:
+$$C = \frac{A}{4} = 0.25 \cdot 10^{-6} V^2/Hz,  D = \frac{B}{4} = 0.25 V^2$$
-$ A = \frac {s_0^2 \cdot T }{4} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{4}\hspace{0.15cm}\underline {= 10^{-6} \,{\rm V^{2}/Hz}}.$
+'''3.'''
-'''2.''' Das Spektrum $Z(f)$ eines Cosinussignals $z(t)$ besteht aus zwei Diracfunktionen bei $± f_T$, jeweils mit dem Gewicht 1/2. Das Leistungsdichtespektrum $Φ_z(f)$ besteht ebenfalls aus den beiden Diracfunktionen, nun aber mit jeweiligem Gewicht 1/4. Die Faltung $Φ_q(f) ∗ Φ_z(f)$ ergibt das Leistungsdichtespektrum $Φ_s(f)$ des Sendesignals. Daraus folgt:
+'''4.'''
-'''Anmerkung:''' Die Leistung pro Bit ergibt sich als das Integral über $Φ_s(f)$:
-'''3.'''  Bei BPSK ist das Quellensignal $q(t)$ bipolar anzusetzen. Im Leistungsdichtespektrum fehlt deshalb die Diraclinie   ⇒   B = 0   und der kontinuierliche LDS–Anteil ist viermal so groß als bei der ASK:
-'''4.''' Für die LDS–Parameter des BPSK–Sendesignals gilt analog zur ASK:
-'''5.'''  Richtig ist nur die erste Aussage. Bei BPSK (bipolares Quellensignal) beinhaltet $Φ_q(f)$ auch dann keine einzige Diraclinie, wenn $g_q(t)$ von der Rechteckform abweicht. Dagegen beinhaltet das unipolare ASK–Quellensignal unendlich viele Diraclinien bei allen Vielfachen von 1/T. Weitere Informationen hierzu finden Sie bei AKF und LDS bei unipolaren Binärsignalen im Buch „Digitalsignalübertragung”.
+'''5.'''
 {{ML-Fuß}}