Kanalcodierung/Grundlegendes zu den Turbocodes: Unterschied zwischen den Versionen
| Zeile 165: | Zeile 165: | ||
*Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (fast) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{–7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.<br><br> | *Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (fast) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{–7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.<br><br> | ||
| − | |||
Wir versuchen nun, den flacheren Abfall der Bitfehlerwahrscheinlichkeit bei größerem $E_{\rm B}/N_0$ zu erklären. Man spricht vom <b>Error Floor</b>: | Wir versuchen nun, den flacheren Abfall der Bitfehlerwahrscheinlichkeit bei größerem $E_{\rm B}/N_0$ zu erklären. Man spricht vom <b>Error Floor</b>: | ||
| − | *Der Grund für dieses asymptotisch schlechtere Verhalten bei besserem Kanal (im Beispiel: ab | + | *Der Grund für dieses asymptotisch schlechtere Verhalten bei besserem Kanal (im Beispiel: ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 \approx 2 \ \rm dB$) ist die Periode $P$ der Coderimpulsantwort $\underline{g}$, wie auf der Seite [[Kanalcodierung/Grundlegendes_zu_den_Turbocodes#Zweite_Voraussetzung_f.C3.BCr_Turbocodes:_Interleaving|Interleaving]] nachgewiesen.<br> |
| − | * | + | *Für $m = 2$ ist die Periode $P = 2^m = 3$. Dadurch ist für $\underline{u} = (1, 1, 1) ⇒ w_{\rm H}(\underline{u}) = 3$ trotz unbegrenzter Impulsantwort $\underline{g}$ die Paritysequenz begrenzt: $\underline{p} = (1, 0, 1)$ ⇒ $w_{\rm H}(\underline{p}) = 2$.<br> |
| − | *Die Sequenz $\underline{u} = (0, \ ... , \ 0, \ 1, \ 0, \ 0, \ 1, \ 0, \ ...)$ ⇒ $U(D) = D^x \cdot (1 + D^P)$ führt ebenfalls zu einem kleinen Hamming–Gewicht $w_{\rm H}(\underline{p})$ am Ausgang, was den iterativen Decodierprozess erschwert.<br> | + | *Die Sequenz $\underline{u} = (0, \ \text{...}\hspace{0.05cm} , \ 0, \ 1, \ 0, \ 0, \ 1, \ 0, \ \text{...}\hspace{0.05cm})$ ⇒ $U(D) = D^x \cdot (1 + D^P)$ führt ebenfalls zu einem kleinen Hamming–Gewicht $w_{\rm H}(\underline{p})$ am Ausgang, was den iterativen Decodierprozess erschwert.<br> |
*Eine gewisse Abhilfe schafft der Interleaver, der dafür sorgt, dass nicht die beiden Sequenzen $\underline{p}_1$ und $\underline{p}_2$ gleichzeitig durch sehr kleine Hamming–Gewichte $w_{\rm H}(\underline{p}_1)$ und $w_{\rm H}(\underline{p}_2)$ belastet sind.<br> | *Eine gewisse Abhilfe schafft der Interleaver, der dafür sorgt, dass nicht die beiden Sequenzen $\underline{p}_1$ und $\underline{p}_2$ gleichzeitig durch sehr kleine Hamming–Gewichte $w_{\rm H}(\underline{p}_1)$ und $w_{\rm H}(\underline{p}_2)$ belastet sind.<br> | ||
| − | *Aus der Grafik erkennt man, dass $\rm Pr(Bitfehler)$ umgekehrt proportional zur Interleavergröße $K$ ist. Das heißt: Bei großem $K$ funktioniert die Entspreizung ungünstiger Eingangssequenzen besser.<br> | + | *Aus der Grafik erkennt man auch, dass $\rm Pr(Bitfehler)$ umgekehrt proportional zur Interleavergröße $K$ ist. Das heißt: Bei großem $K$ funktioniert die Entspreizung ungünstiger Eingangssequenzen besser.<br> |
| − | *Allerdings gilt die Näherung $K \cdot {\rm Pr(Bitfehler) = const.}$ nur für größere $E_{\rm B}/N_0$–Werte ⇒ | + | *Allerdings gilt die Näherung $K \cdot {\rm Pr(Bitfehler) = const.}$ nur für größere $E_{\rm B}/N_0$–Werte ⇒ kleine Bitfehlerwahrscheinlichkeiten. Der beschriebene Effekt tritt zwar auch bei kleinerem $E_{\rm B}/N_0$ auf, doch sind dann die Auswirkungen auf die $\rm Pr(Bitfehler)$ geringer.<br><br> |
| − | Dagegen gilt der flachere Verlauf der Blockfehlerwahrscheinlichkeit (grüne Kurve weitgehend unabhängig von der Interleavergröße $K$, also sowohl für $K = 1000$ als auch für $K = 10000$. Im Bereich ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 > 2 \ \rm dB$ dominieren | + | Dagegen gilt der flachere Verlauf der Blockfehlerwahrscheinlichkeit (grüne Kurve) weitgehend unabhängig von der Interleavergröße $K$, also sowohl für $K = 1000$ als auch für $K = 10000$. Im Bereich ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 > 2 \ \rm dB$ dominieren nämlich Einzelfehler, so dass hier die Näherung ${\rm Pr(Blockfehler)} \approx {\rm Pr(Bitfehler)} \cdot K$ gültig ist.<br> |
| − | Die | + | {{BlaueBox|TEXT= |
| + | $\text{Fazit:}$ Die beispielhaft gezeigten Kurven für Bitfehlerwahrscheinlichkeit und Blockfehlerwahrscheinlichkeit gelten qualitativ auch für $m > 2$, zum Beispiel für den Turbocode von UMTS und LTE (jeweils $m = 3$), der in [[Aufgabe 4.10]] analysiert wird. Es ergeben sich aber einige quantitative Unterschiede: | ||
*Die Kurve verläuft bei kleinem $E_{\rm B}/N_0$ steiler und der Abstand von der Shannongrenze ist etwas geringer als im hier gezeigten Beispiel für $m = 2$.<br> | *Die Kurve verläuft bei kleinem $E_{\rm B}/N_0$ steiler und der Abstand von der Shannongrenze ist etwas geringer als im hier gezeigten Beispiel für $m = 2$.<br> | ||
| − | *Auch für größeres $m$ gibt es einen <i>Error Floor</i>. Der Knick in den dargestellten Kurven erfolgt aber später, also bei kleineren Fehlerwahrscheinlichkeiten.<br> | + | *Auch für größeres $m$ gibt es einen <i>Error Floor</i>. Der Knick in den dargestellten Kurven erfolgt aber später, also bei kleineren Fehlerwahrscheinlichkeiten.}}<br> |
== Seriell verkettete Turbocodes – SCCC == | == Seriell verkettete Turbocodes – SCCC == | ||
Version vom 8. Dezember 2017, 09:41 Uhr
Inhaltsverzeichnis
- 1 Grundstruktur eines Turbocodes
- 2 Weitere Modifizierung der Turbocode–Grundstruktur
- 3 Erste Voraussetzung für Turbocodes: Rekursive Komponentencodes
- 4 Zweite Voraussetzung für Turbocodes: Interleaving
- 5 Symbolweise iterative Decodierung eines Turbocodes
- 6 Leistungsfähigkeit der Turbocodes
- 7 Seriell verkettete Turbocodes – SCCC
- 8 Einige Anwendungsgebiete für Turbocodes
- 9 Aufgaben
- 10 Quellenverzeichnis
Grundstruktur eines Turbocodes
Alle heute (2017) aktuellen Kommunikationssysteme wie UMTS (Universal Mobile Telecommunications System ⇒ 3. Mobilfunkgeneration) und LTE (Long Term Evolution ⇒ 4. Mobilfunkgeneration) verwenden das Konzept der symbolweisen iterativen Decodierung. Dass dies so ist, steht unmittelbar mit der Erfindung der Turbocodes im Jahre 1993 durch C. Berrou, A. Glavieux und P. Thitimajshima in Zusammenhang, denn erst mit diesen Codes konnte man sich der Shannon–Grenze mit vertretbarem Decodieraufwand annähern.
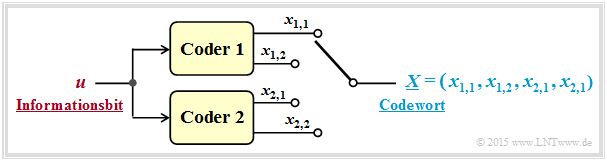
Turbocodes ergeben sich durch die parallele oder serielle Verkettung von Faltungscodes. Die Grafik zeigt die parallele Verkettung zweier Codes mit den Parametern $k = 1, \ n = 2$ ⇒ Rate $R = 1/2$.
In dieser Darstellung bezeichnet:
- $u$ das aktuell betrachtete Bit der Informationssequenz $\underline{u}$,
- $x_{i,\hspace{0.03cm}j}$ das aktuell betrachtete Bit am Ausgang $j$ von Coder $i$ (mit $1 ≤ i ≤ 2, \ 1 ≤ j ≤ 2)$,
- $\underline{X} = (x_{1,\hspace{0.03cm}1}, \ x_{1,\hspace{0.03cm}2}, \ x_{2,\hspace{0.03cm}1}, \ x_{2,\hspace{0.03cm}2})$ das Codewort für das aktuelle Informationsbit $u$.
Die resultierende Rate des verketteten Codiersystems ist somit $R = 1/4$.
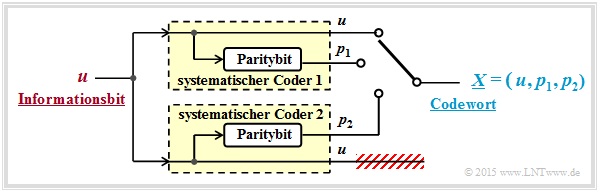
Verwendet man systematische Komponentencodes, so ergibt sich das folgende Modell:
Die Modifikationen gegenüber der oberen Grafik lassen sich wie folgt begründen:
- Bei systematischen Codes $C_1$ und $C_2$ ist sowohl $x_{1,\hspace{0.03cm}1} = u$ als auch $x_{2,\hspace{0.03cm}1} = u$. Deshalb kann man auf die Übertragung eines redundanten Bits (zum Beispiel $x_{2,\hspace{0.03cm}2}$) verzichten.
- Mit dieser Reduktion ergibt sich ein Rate–1/3–Turbocode mit den Parametern $k = 1$ und $n = 3$. Das Codewort lautet mit den Paritybits $p_1$ und $p_2$ von Coder 1 bzw. Coder 2: $\underline{X} = \left (u, p_1, p_2 \right )\hspace{0.05cm}.$
Weitere Modifizierung der Turbocode–Grundstruktur
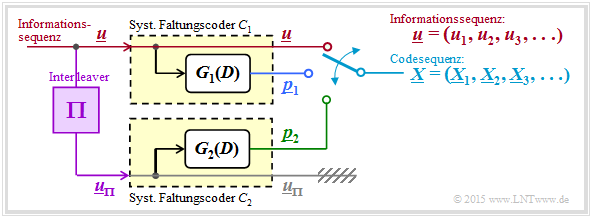
Im Folgenden gehen wir stets von einem noch etwas weiter modifizierten Turbocoder–Modell aus:
- Wie es für die Beschreibung von Faltungscodes erforderlich ist, liegt nun am Eingang anstelle des isolierten Informationsbits $u$ die Informationssequenz $\underline{u} = (u_1, \ u_2, \ \text{...}\hspace{0.05cm} , \ u_i , \ \text{...}\hspace{0.05cm} )$ an.
- Die Codewortsequenz wird mit $\underline{x} = (\underline{X}_1, \underline{X}_2, \ \text{...}\hspace{0.05cm} , \ \underline{X}_i, \ \text{...}\hspace{0.05cm} )$ bezeichnet. Um Verwechslungen zu vermeiden, wurden vorne die Codeworte $\underline{X}_i = (u, \ p_1, \ p_2)$ mit Großbuchstaben eingeführt.
- Die Coder $\mathcal{C}_1$ und $\mathcal{C}_2$ werden (zumindest gedanklich) als Digitale Filter konzipiert und sind somit durch die Übertragungsfunktionen $G_1(D)$ und $G_2(D)$ darstellbar.
- Aus verschiedenen Gründen ⇒ siehe übernächste Seite sollte die Eingangssequenz des zweiten Coders ⇒ $\underline{u}_{\pi}$ gegenüber der Sequenz $\underline{u}$ durch einen Interleaver $(\Pi)$ verwürfelt sein.
- Somit spricht nichts dagegen, die beiden Coder gleich zu wählen: $G_1(D) = G_2(D) = G_3(D)$. Ohne Interleaver würde dies die Korrekturfähigkeit extrem einschränken.
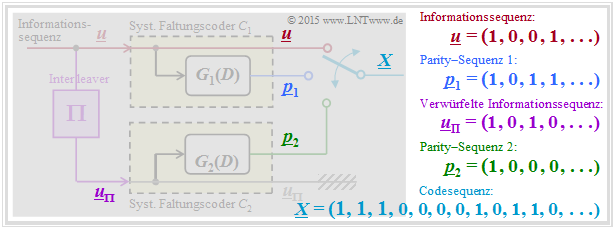
$\text{Beispiel 1:}$ Die Grafik zeigt die verschiedenen Sequenzen in angepassten Farben. Anzumerken ist:
- Für $\underline{u}_{\pi}$ ist eine $3×4$–Interleaver–Matrix entsprechend Aufgabe 4.8Z berücksichtigt.
- Die Paritysequenzen ergeben sich gemäß $G_1(D) = G_2(D) = 1 + D^2$ ⇒ siehe Aufgabe 4.8.
Erste Voraussetzung für Turbocodes: Rekursive Komponentencodes
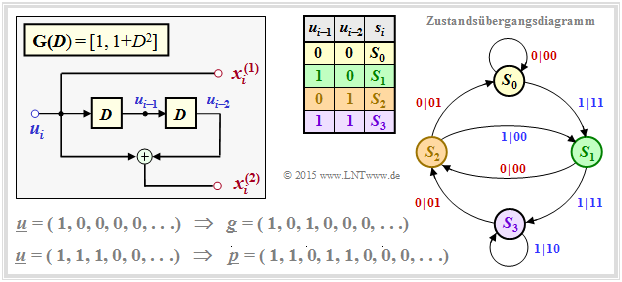
Nichtrekursive Übertragungsfunktionen zur Erzeugung der Paritysequenzen bewirken einen Turbocode mit unzureichend kleiner Minimaldistanz. Grund für diese Unzulänglichkeit ist die endliche Impulsantwort $\underline{g} = (1, \ g_2, \ \text{...}\hspace{0.05cm} , \ g_m, \ 0, \ 0, \ \text{...}\hspace{0.05cm} )$ mit $g_2, \ \text{...}\hspace{0.05cm} , \ g_m ∈ \{0, 1\}$. Hierbei bezeichnet $m$ das Codegedächtnis.
Die Grafik zeigt das Zustandsübergangsdiagramm für das Beispiel $\mathbf{G}(D) = [1, \ 1 + D^2]$. Die Übergänge sind mit „$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i p_i$” beschriftet. Die Abfolge $S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \ \text{...}\hspace{0.05cm} \ $ führt bezüglich des Eingangs zur Informationssequenz $\underline{u} = (1, 0, 0, 0, 0, \ \text{...}\hspace{0.05cm})$ und bezüglich des jeweils zweiten Codesymbols zur Paritysequenz $\underline{p} = (1, 0, 1, 0, 0, \ \text{...}\hspace{0.05cm})$ ⇒ identisch mit der Impulsantwort $\underline{g}$ ⇒ Gedächtnis $m = 2$.
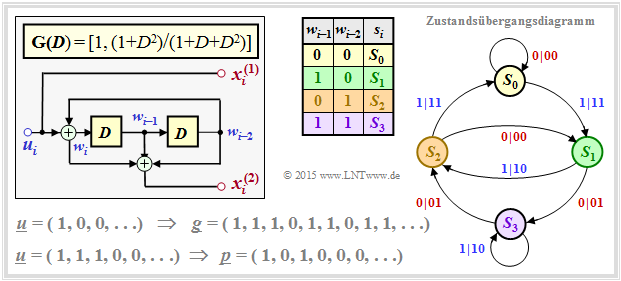
Die untere Grafik gilt für einen so genannten RSC–Code (Recursive Systematic Convolutional) entsprechend $\mathbf{G}(D) = [1, \ (1+ D^2)/(1 + D + D^2)]$. Hier führt die Folge $S_0 → S_1 → S_3 → S_2 → S_1 → S_3 → S_2 → \ \text{...}\hspace{0.05cm} \ $ zur Impulsantwort $\underline{g} = (1, 1, 1, 0, 1, 1, 0, 1, 1, \ \text{...}\hspace{0.05cm})$. Diese Impulsantwort setzt sich aufgrund der Schleife $S_1 → S_3 → S_2 → S_1$ bis ins Unendliche fort. Dies ermöglicht bzw. erleichtert die iterative Decodierung.
Mehr Details zu den Beispielen auf dieser Seite finden Sie in der Aufgabe 4.8 und der Aufgabe 4.9.
Zweite Voraussetzung für Turbocodes: Interleaving
Es ist offensichtlich, dass bei $G_1(D) = G_2(D)$ ein Interleaver $(\Pi)$ unerlässlich ist. Ein weiterer Grund ist, dass die Apriori–Information als unabhängig vorausgesetzt wird. Somit sollten benachbarte (und somit möglicherweise stark abhängige) Bits für den jeweils anderen Teilcode weit auseinander liegen.
Für jeden RSC–Code ⇒ unendliche Impulsantwort $\underline{g}$ ⇒ gebrochen–rationale Übertragungsfunktion $G(D)$ gibt es nämlich gewisse Eingangssequenzen $\underline{u}$, die zu sehr kurzen Paritysequenzen $\underline{p} = \underline{u} ∗ \underline{g}$ mit geringem Hamming–Gewicht $w_{\rm H}(\underline{p})$ führen.
Eine solche Sequenz ist beispielsweise in der unteren Grafik auf der letzten Seite angegeben: $\underline{u} = (1, 1, 1, 0, 0, \ \text{...}\hspace{0.05cm})$. Dann gilt für die Ausgangssequenz:
- \[P(D) = U(D) \cdot G(D) = (1+D+D^2) \cdot \frac{1+D^2}{1+D+D^2}= 1+D^2\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}\hspace{0.05cm})\hspace{0.05cm}. \]
$\text{Sinn und Zweck:}$ Durch Interleaving (deutsch: Verwürfelung) wird nun mit großer Wahrscheinlichkeit sichergestellt, dass diese Sequenz $\underline{u} = (1, 1, 1, 0, 0, \ \text{...}\hspace{0.05cm})$ in eine Sequenz $\underline{u}_{\pi}$ gewandelt wird,
- die zwar ebenfalls nur drei Einsen beinhaltet,
- deren Ausgangssequenz aber durch ein großes Hamming–Gewicht $w_{\rm H}(\underline{p})$ gekennzeichnet ist.
Somit gelingt es dem Decoder, solche „Problemsequenzen” iterativ aufzulösen.
Zur folgenden Beschreibung der Interleaver verwendet wir die Zuordnung $I_{\rm In} → I_{\rm Out}$. Diese Bezeichnungen stehen für die Indizes von Ausgangs– bzw. Eingangsfolge. Die Interleavergröße wird mit $I_{\rm max}$ benannt.
Es gibt mehrere, grundsätzlich verschiedene Interleaver–Konzepte:
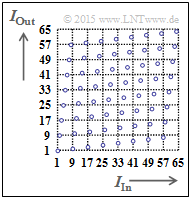
Bei einem Block–Interleaver füllt man eine Matrix mit $S$ Spalten und $Z$ Zeilen spaltenweise und liest die Matrix zeilenweise aus. Damit wird ein Informationsblock mit $I_{\rm max} = S \cdot Z \ \rm Bit$ deterministisch verwürfelt.
Die rechte Grafik verdeutlicht das Prinzip für $I_{\rm max} = 64$ ⇒ $1 ≤ I_{\rm In} < 65$ und $1 ≤ I_{\rm Out} < 65$. Die Reihenfolge der Ausgangsbits lautet dann: $1, 9, 17, 25, 33, 41, 49, 57, 2, 10, 18, \ \text{...}\hspace{0.05cm} , 48, 56, 64.$
Mehr Informationen zum Block–Interleaving gibt es in derAufgabe 4.8Z.
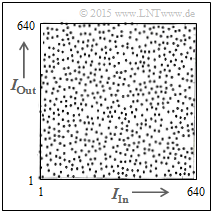
Turbocodes verwenden oft den $S$–Random–Interleaver. Dieser pseudozufällige Algorithmus mit dem Parameter „$S$” garantiert, dass zwei am Eingang weniger als $S$ auseinander liegende Indizes am Ausgang mindestens im Abstand $S + 1$ auftreten. Die linke Grafik zeigt die $S$–Random–Kennlinie $I_{\rm Out}(I_{\rm In})$ für $I_{\rm max} = 640$.
Auch dieser Algorithmus ist deterministisch, und man kann die Verwürfelung im Decoder rückgängig machen ⇒ De–Interleaving. Die Verteilung wirkt trotzdem „zufälliger” als bei Block–Interleaving.
Symbolweise iterative Decodierung eines Turbocodes
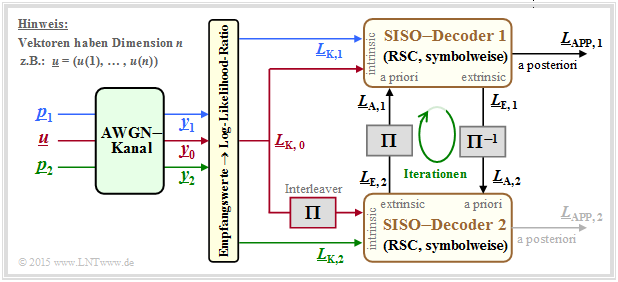
Die Decodierung eines Turbocodes geschieht grundsätzlich wie im Abschnitt Symbolweise Soft–in Soft–out_Decodierung beschrieben. Aus der folgenden Grafik erkennt man aber auch einige nur für den Turbodecoder zutreffende Besonderheiten.
Vorausgesetzt ist ein Rate–1/3–Turbocode entsprechend der Beschreibung auf der ersten Seite dieses Abschnitts. Auch die Farbgebung für die Informationssequenz $\underline{u}$ und die beiden Paritysequenzen $\underline{p}_1$ und $\underline{p}_2$ sind an die früheren Grafiken angepasst. Weiter ist zu bemerken:
- Die Empfangsvektoren $\underline{y}_0, \underline{y}_1$ und $\underline{y}_2$ sind reellwertig und liefern die jeweilige Soft–Information bezüglich der Informationssequenz $\underline{u}$ sowie der Sequenzen $\underline{p}_1$ (Parity für Coder 1) und $\underline{p}_2$ (Parity für Coder 2).
- Der Decoder 1 erhält die erforderliche intrinsische Information in Form der $L$–Werte $L_{\rm K,\hspace{0.03cm} 0}$ (aus $\underline{y}_0$) und $L_{\rm K,\hspace{0.03cm}1}$ (aus $\underline{y}_1$) über jedes einzelne Bit der Sequenzen $\underline{u}$ und $\underline{p}_1$.
- Beim zweiten Decoder ist auch die Verwürfelung der Informationssequenz $\underline{u}$ durch den Interleaver zu berücksichtigen. Die zu verarbeitenden $L$–Werte sind somit $\pi(L_{\rm K, \hspace{0.03cm}0}$ und $L_{\rm K, \hspace{0.03cm}2}$.
- Beim allgemeinen SISO–Decoder wurde der Informationsaustausch zwischen den beiden Komponentendecodern mit $\underline{L}_{\rm A, \hspace{0.03cm}2} = \underline{L}_{\rm E, \hspace{0.03cm}1}$ sowie $\underline{L}_{\rm A, \hspace{0.03cm}1} = \underline{L}_{\rm E, \hspace{0.03cm}2}$ angegeben. Ausgeschrieben auf Bitebene bedeuten diese Gleichungen mit $1 ≤ i ≤ n$:
- \[L_{\rm A, \hspace{0.03cm}2}(i) = L_{\rm E, \hspace{0.03cm}1}(i) \hspace{0.5cm}{\rm bzw.}\hspace{0.5cm} L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}(i) \hspace{0.03cm}.\]
- Beim Turbodecoder muss bei diesem Informationsaustausch auch der Interleaver berücksichtigt werden. Dann gilt wieder für $i = 1, \ \text{...}\hspace{0.05cm} , \ n$:
- \[L_{\rm A, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) = L_{\rm E, \hspace{0.03cm}1}(i) \hspace{0.5cm}{\rm bzw.}\hspace{0.5cm} L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) \hspace{0.05cm}.\]
- Der Aposteriori–$L$–Wert wird in obigem Modell (willkürlich) vom Decoder 1 abgegeben. Dies lässt sich damit begründen, dass eine Iteration für einen zweifachen Informationsaustausch steht.
Leistungsfähigkeit der Turbocodes
Wir betrachten wieder wie auf den letzten Seiten den Rate–1/3–Turbocode
- mit gleichen Filterfunktionen $G_1(D) = G_2(D) = (1 + D^2)/(1 + D + D^2)$ ⇒ Gedächtnis $m = 2$,
- mit der Interleavergröße $K$; zunächst gelte $K = 10000,$
- eine ausreichende Anzahl an Iterationen $(I = 20)$, hier nahezu gleichzusetzen mit „$I → ∞$”.
Die beiden RSC–Komponentencodes sind jeweils auf $K$ Bit terminiert. Deshalb gruppieren wir
- die Informationssequenz $\underline{u}$ zu Blöcken mit je $K$ Informationsbits, und
- die Codesequenz $\underline{x}$ zu Blöcken mit je $N = 3 \cdot K$ Codebits.
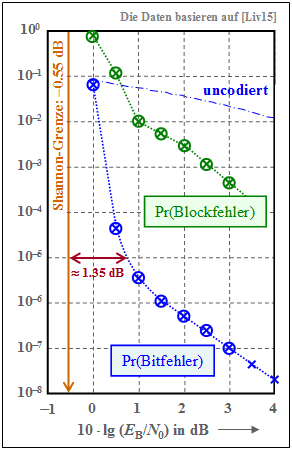
Die Grafik zeigt als grüne Kurve in doppelt–logarithmischer Darstellung die Blockfehlerwahrscheinlichkeit ⇒ ${\rm Pr(Blockfehler)}$ beim AWGN–Kanal in Abhängigkeit der Kenngröße $10 \cdot {\rm lg} \, (E_{\rm B}/N_0)$. Die Daten entstammen dem Vorlesungsskript [Liv15][1].
Man erkennt:
- Die mit Kreuzen markierten Punkte ergaben sich aus den Gewichtsfunktionen des Turbocodes mit Hilfe der Union Bound. Simulationsergebnisse – in der Grafik durch Kreise markiert – sind nahezu deckungsgleich mit den berechneten Werten.
- Die Union Bound ist nur eine obere Schranke, basierend auf ML–Decodierung. Der iterative Decoder ist suboptimal (also schlecher als ML). Diese beiden Effekte heben sich scheinbar auf.
- Etwa bei $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 1 \ \rm dB$ ist ein Knick im (grünen) Kurvenverlauf festzustellen, der mit der Steigungsänderung von ${\rm Pr(Bitfehler)}$ ⇒ blaue Kurve korrespondiert. Die Erklärung folgt unten.
Die blauen Kreuze (Berechnung) und die blauen Kreise (Simulation) bezeichnen die Bitfehlerwahrscheinlichkeit für die Interleavergröße $K = 10000$ . Als Vergleichskurve ist die (strichpunktierte) Kurve für uncodierte Übertragung eingezeichnet.
Anzumerken ist:
- Bei kleinen Abszissenwerten ist der Kurvenabfall in der gewählten Darstellung nahezu linear und ausreichend steil. Zum Beispiel benötigt man für ${\rm Pr(Bitfehler)} = 10^{–5}$ mindestens $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, 0.8 \ \rm dB$.
- Im Vergleich zur Shannon–Grenze, die sich für die Coderate $R = 1/3$ zu $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.
- Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (fast) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{–7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.
Wir versuchen nun, den flacheren Abfall der Bitfehlerwahrscheinlichkeit bei größerem $E_{\rm B}/N_0$ zu erklären. Man spricht vom Error Floor:
- Der Grund für dieses asymptotisch schlechtere Verhalten bei besserem Kanal (im Beispiel: ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 \approx 2 \ \rm dB$) ist die Periode $P$ der Coderimpulsantwort $\underline{g}$, wie auf der Seite Interleaving nachgewiesen.
- Für $m = 2$ ist die Periode $P = 2^m = 3$. Dadurch ist für $\underline{u} = (1, 1, 1) ⇒ w_{\rm H}(\underline{u}) = 3$ trotz unbegrenzter Impulsantwort $\underline{g}$ die Paritysequenz begrenzt: $\underline{p} = (1, 0, 1)$ ⇒ $w_{\rm H}(\underline{p}) = 2$.
- Die Sequenz $\underline{u} = (0, \ \text{...}\hspace{0.05cm} , \ 0, \ 1, \ 0, \ 0, \ 1, \ 0, \ \text{...}\hspace{0.05cm})$ ⇒ $U(D) = D^x \cdot (1 + D^P)$ führt ebenfalls zu einem kleinen Hamming–Gewicht $w_{\rm H}(\underline{p})$ am Ausgang, was den iterativen Decodierprozess erschwert.
- Eine gewisse Abhilfe schafft der Interleaver, der dafür sorgt, dass nicht die beiden Sequenzen $\underline{p}_1$ und $\underline{p}_2$ gleichzeitig durch sehr kleine Hamming–Gewichte $w_{\rm H}(\underline{p}_1)$ und $w_{\rm H}(\underline{p}_2)$ belastet sind.
- Aus der Grafik erkennt man auch, dass $\rm Pr(Bitfehler)$ umgekehrt proportional zur Interleavergröße $K$ ist. Das heißt: Bei großem $K$ funktioniert die Entspreizung ungünstiger Eingangssequenzen besser.
- Allerdings gilt die Näherung $K \cdot {\rm Pr(Bitfehler) = const.}$ nur für größere $E_{\rm B}/N_0$–Werte ⇒ kleine Bitfehlerwahrscheinlichkeiten. Der beschriebene Effekt tritt zwar auch bei kleinerem $E_{\rm B}/N_0$ auf, doch sind dann die Auswirkungen auf die $\rm Pr(Bitfehler)$ geringer.
Dagegen gilt der flachere Verlauf der Blockfehlerwahrscheinlichkeit (grüne Kurve) weitgehend unabhängig von der Interleavergröße $K$, also sowohl für $K = 1000$ als auch für $K = 10000$. Im Bereich ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 > 2 \ \rm dB$ dominieren nämlich Einzelfehler, so dass hier die Näherung ${\rm Pr(Blockfehler)} \approx {\rm Pr(Bitfehler)} \cdot K$ gültig ist.
$\text{Fazit:}$ Die beispielhaft gezeigten Kurven für Bitfehlerwahrscheinlichkeit und Blockfehlerwahrscheinlichkeit gelten qualitativ auch für $m > 2$, zum Beispiel für den Turbocode von UMTS und LTE (jeweils $m = 3$), der in Aufgabe 4.10 analysiert wird. Es ergeben sich aber einige quantitative Unterschiede:
- Die Kurve verläuft bei kleinem $E_{\rm B}/N_0$ steiler und der Abstand von der Shannongrenze ist etwas geringer als im hier gezeigten Beispiel für $m = 2$.
- Auch für größeres $m$ gibt es einen Error Floor. Der Knick in den dargestellten Kurven erfolgt aber später, also bei kleineren Fehlerwahrscheinlichkeiten.
Seriell verkettete Turbocodes – SCCC
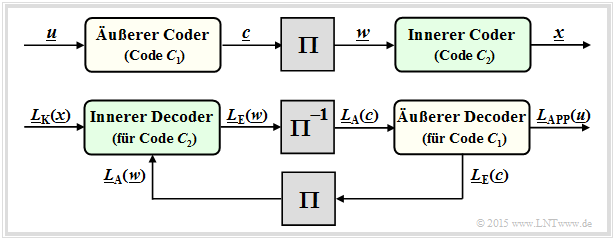
Die bisher betrachteten Turbocodes werden manchmal auch als Parallel Concatenated Convolutional Codes (PCCC) bezeichnet. Einige Jahre nach Berrou's Erfindung wurden von anderen Autoren auch Serial Concatenated Convolutional Codes (SCCC) entsprechend folgender Grafik vorgeschlagen.
- Die Informationssequenz $\underline{u}$ liegt am äußeren Faltungscoder $C_1$ an. Dessen Ausgangssequenz sei $\underline{c}$.
- Nach dem Interleaver $(\Pi)$ folgt der innere Faltungscoder $C_2$. Die Codesequenz wird $\underline{x}$ genannt.
- Die resultierende Coderate ist $R = R_1 \cdot R_2$. Bei Rate–1/2–Komponentencodes ist $R = 1/4$.
Die untere Grafik zeigt den SCCC–Decoder und verdeutlicht die Verarbeitung der $L$–Werte und den Austausch der extrinsischen Information zwischen den beiden Komponentencoder:
- Der innere Decoder (für den Code $C_2$) erhält vom Kanal die intrinsische Information $\underline{L}_{\rm K}(\underline{x})$ und vom äußeren Decoder (nach Interleaving) die Apriori–Information $\underline{L}_{\rm A}(\underline{w})$ mit $\underline{w} = \pi(\underline{c})$. An den äußeren Decoder wird die extrinsische Information $\underline{L}_{\rm E}(\underline{w})$ abgegeben.
- Der äußere Decoder (für $C_1$) verarbeitet die Apriori–Information $\underline{L}_{\rm A}(\underline{c})$, also die extrinsische Information $\underline{L}_{\rm E}(\underline{w})$ nach dem De–Interleaving. Er liefert die extrinsische Information $\underline{L}_{\rm E}(\underline{c})$.
- Nach hinreichend vielen Iterationen ergibt sich das das gewünschte Decodierergebnis in Form der Aposteriori–$L$–Werte $\underline{L}_{\rm APP}(\underline{u})$ der Informationssequenz $\underline{u}$.
Wichtig für seriell verkettete Faltungscodes ist, dass der innere Code rekursiv ist (also ein RSC–Code). Der äußere Code $C_1$ kann auch nichtrekursiv sein. Zur Leistungsfähigkeit solcher Codes ist anzumerken:
- SCCCs sind bei großem $E_{\rm B}/N_0$ besser als PCCCs ⇒ niedrigerer Error Floor. Die Aussage gilt schon für SCCC–Komponentencodes mit Gedächtnis $m = 2$ (nur vier Trelliszustände), während bei PCCC das Gedächtnis $m = 3$ bzw. $m = 4$ (acht bzw. sechzehn Trelliszustände) sein sollte.
- Im unteren Bereich (kleines $E_{\rm B}/N_0$) ist dagegen der beste seriell verkettete Faltungscode (SCCC) um einige Zehntel Dezibel schlechter als der vergleichbare Turbocode gemäß Berrou (PCCC). Entsprechend größer ist auch der Abstand von der Shannongrenze.
Einige Anwendungsgebiete für Turbocodes
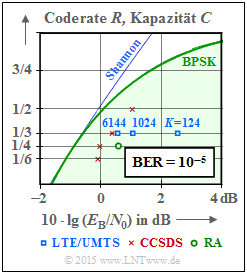
In fast allen neueren Kommunikationssystemen (nach 1993 standardisiert) werden Turbocodes eingesetzt. Die Grafik zeigt deren Leistungsfähigkeit beim AWGN–Kanal im Vergleich zur Shannonschen Kanalkapazität (blaue Kurve).
Der grün hinterlegte Bereich „BPSK” gibt die Shannongrenze für Nachrichtensystemee mit binärem Eingang an, mit der nach dem Kanalcodierungstheorem eine fehlerfreie Übertragung gerade noch möglich ist.
Anzumerken ist, dass hier für die eingezeichneten Kanalcodes von standardisierten Systemen die Fehlerrate $10^{–5}$ zugrunde liegt, während die informationstheoretischen Kapazitätskurven (Shannon, BPSK) für die Fehlerwahrscheinlichkeit $0$ gelten.
- Die blauen Rechtecke markieren die Turbocodes für UMTS. Diese sind Rate–1/3–Codes mit Gedächtnis $m = 3$. Die Leistungsfähigkeit hängt stark von der Interleavergröße ab. Mit $K = 6144$ liegt dieser Code nur etwa $1 \ \rm dB$ rechts von der Shannon–Grenze. LTE verwendet die gleichen Turbocodes. Geringfügige Unterschiede ergeben sich aufgrund des unterschiedlichen Interleavers.
- Die roten Kreuze markieren die Turbocodes nach CCSDS (Consultative Comittee for Space Data Systems), entwickelt für den Einsatz bei fernen Weltraummissionen. Diese Klasse geht von der einheitlichen Interleavergröße $K = 6920$ aus und stellt Codes der Rate $1/6, 1/4, 1/3$ und $1/2$ zur Verfügung. Die niedrigsten Coderaten erlauben einen Betrieb mit $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0 \ \rm dB$.
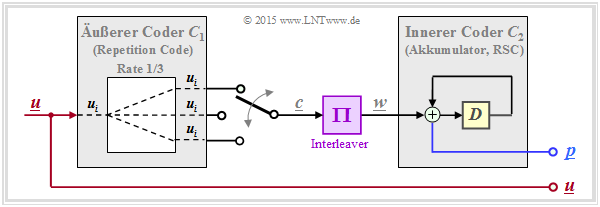
- Der grüne Kreis steht für einen sehr einfachen Repeat–Accumulate (RA) Code, einem seriell–verketteten Turbocode. Der äußere Decoder verwendet einen Wiederholungscode (englisch: Repetition Code), im gezeichneten Beispiel mit der Rate $R = 1/3$. Nach dem Interleaver folgt ein RSC–Code mit $G(D) = 1/(1 + D)$ ⇒ Gedächtnis $m = 1$. Bei systematischer Ausführung ist die Gesamtcoderate $R = 1/4$ (zu jedem Informationsbit noch drei Paritybits). Aus der oberen Grafik erkennt man, dass dieser einfache RA–Code überraschend gut ist. Mit der Interleavergröße $K = 300000$ beträgt der Abstand von der Shannon–Grenze lediglich ca. $1.5 \ \rm dB$.
In der oberen Grafik nicht eingetragen sind die Turbocodes für den Standard DVB Return Channel Terrestrial (RCS) sowie für den WiMax–Standard (IEEE 802.16), die ähnliche Turbocodes benutzen.
Aufgaben
A4.8 Wiederholung zu den Faltungscodes
Zusatzaufgaben:4.8 Grundlegendes zum Interleaving
A4.9 Wiederholung zu den RSC-Codes
Quellenverzeichnis
- ↑ Liva, G.: Channels Codes for Iterative Decoding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2015.