Informationstheorie/Verschiedene Entropien zweidimensionaler Zufallsgrößen: Unterschied zwischen den Versionen
| Zeile 30: | Zeile 30: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Wir beziehen uns nochmals auf | + | $\text{Beispiel 1:}$ Wir beziehen uns nochmals auf die Beispiele auf der Seite [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|Verbundwahrscheinlichkeit und Verbundentropie]] im letzten Kapitel. |
| − | Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RB}(R, B)$ im dortigen | + | Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RB}(R, B)$ im dortigen $\text{Beispiel 5}$ mit den Parametern |
*$R$ ⇒ Augenzahl des roten Würfels und | *$R$ ⇒ Augenzahl des roten Würfels und | ||
*$B$ ⇒ Augenzahl des blauen Würfels | *$B$ ⇒ Augenzahl des blauen Würfels | ||
| − | |||
| − | Bei der 2D Wahrscheinlichkeitsfunktion $P_{RS}(R, S)$ im | + | sind die Mengen $P_{RB}$ und $\text{supp}(P_{RB})$ identisch. Hier sind alle $6^2 = 36$ Felder mit Werten ungleich Null belegt. |
| + | |||
| + | Bei der 2D Wahrscheinlichkeitsfunktion $P_{RS}(R, S)$ im $\text{Beispiel 6}$ mit den Parametern | ||
*$R$ ⇒ Augenzahl des roten Würfels und | *$R$ ⇒ Augenzahl des roten Würfels und | ||
*$S = R + B$ ⇒ Summe der beiden Würfel | *$S = R + B$ ⇒ Summe der beiden Würfel | ||
| − | gibt es $6 · 11 = 66$ Felder, von denen allerdings viele leer sind, also für die Wahrscheinlichkeit „0”. | + | |
| − | *Die Teilmenge $\text{supp}(P_{RS})$ beinhaltet dagegen nur die 36 schraffierten Felder mit von | + | gibt es $6 · 11 = 66$ Felder, von denen allerdings viele leer sind, also für die Wahrscheinlichkeit „0” stehen. |
| + | *Die Teilmenge $\text{supp}(P_{RS})$ beinhaltet dagegen nur die 36 schraffierten Felder mit von Null verschiedenen Wahrscheinlichkeiten. | ||
*Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da für $x → 0$ der Grenzwert $x · \log_2 ({1}/{x}) = 0$ ist.}} | *Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da für $x → 0$ der Grenzwert $x · \log_2 ({1}/{x}) = 0$ ist.}} | ||
| Zeile 49: | Zeile 51: | ||
==Bedingte Wahrscheinlichkeit und bedingte Entropie == | ==Bedingte Wahrscheinlichkeit und bedingte Entropie == | ||
<br> | <br> | ||
| − | Im Buch „Stochastische Signaltheorie” wurden für den Fall zweier Ereignisse $X$ und $Y$ die folgenden [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit_.281.29|bedingten Wahrscheinlichkeiten]] angegeben ⇒   '''Satz von Bayes''': | + | Im Buch „Stochastische Signaltheorie” wurden für den Fall zweier Ereignisse $X$ und $Y$ die folgenden [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit_.281.29|bedingten Wahrscheinlichkeiten]] angegeben ⇒ '''Satz von Bayes''': |
:$${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} | :$${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} | ||
| Zeile 62: | Zeile 64: | ||
| − | {{BlaueBox| | + | {{BlaueBox|TEXT= |
| − | TEXT= | + | $\text{Definitionen:}$ |
| + | |||
| + | Die '''bedingte Entropie''' (englisch: ''Conditional Entropy'') der Zufallsgröße $X$ unter der Bedingung $Y$ lautet: | ||
:$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | :$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | ||
| Zeile 72: | Zeile 76: | ||
In gleicher Weise erhält man für die zweite bedingte Entropie: | In gleicher Weise erhält man für die zweite bedingte Entropie: | ||
| − | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | + | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} |
\hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} | ||
\hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} | \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} | ||
| Zeile 78: | Zeile 82: | ||
| − | Im Argument der Logarithmusfunktion steht stets eine bedingte Wahrscheinlichkeitsfunktion ⇒ $P_{X\hspace{0.03cm}| \hspace{0.03cm}Y}(·)$ bzw. $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(·)$, während zur Erwartungswertbildung die Verbundwahrscheinlichkeit $P_{XY}(·)$ benötigt wird. | + | Im Argument der Logarithmusfunktion steht stets eine bedingte Wahrscheinlichkeitsfunktion ⇒ $P_{X\hspace{0.03cm}| \hspace{0.03cm}Y}(·)$ bzw. $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(·)$, während zur Erwartungswertbildung die Verbundwahrscheinlichkeit ⇒ $P_{XY}(·)$ benötigt wird. |
| + | |||
Für die bedingten Entropien gibt es folgende Begrenzungen: | Für die bedingten Entropien gibt es folgende Begrenzungen: | ||
| − | *Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich | + | *Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich Null. Aus $H(X|Y) = 0$ folgt direkt auch $H(Y|X) = 0$. Beides ist nur für [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Disjunkte_Mengen|disjunkte Mengen]] $X$ und $Y$ möglich. |
*Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese Aussage ist einleuchtend, wenn man sich bewusst macht, dass man für „Entropie” synonym auch „Unsicherheit” verwenden kann. | *Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese Aussage ist einleuchtend, wenn man sich bewusst macht, dass man für „Entropie” synonym auch „Unsicherheit” verwenden kann. | ||
| − | *Denn: Die Unsicherheit bezüglich $X$ kann nicht dadurch größer werden, dass man $Y$ kennt. Außer bei statistischer Unabhängigkeit ⇒ $H(X|Y) = H(X)$ gilt stets $H(X|Y) < H(X)$. | + | *Denn: Die Unsicherheit bezüglich der Menge $X$ kann nicht dadurch größer werden, dass man $Y$ kennt. Außer bei statistischer Unabhängigkeit ⇒ $H(X|Y) = H(X)$ gilt stets $H(X|Y) < H(X)$. |
*Wegen $H(X) ≤ H(XY)$, $H(Y) ≤ H(XY)$ gilt somit auch $H(X|Y) ≤ H(XY)$ und $H(Y|X) ≤ H(XY)$. Eine bedingte Entropie kann also nie größer werden als die Verbundentropie. | *Wegen $H(X) ≤ H(XY)$, $H(Y) ≤ H(XY)$ gilt somit auch $H(X|Y) ≤ H(XY)$ und $H(Y|X) ≤ H(XY)$. Eine bedingte Entropie kann also nie größer werden als die Verbundentropie. | ||
| − | {{GraueBox| | + | {{GraueBox|TEXT= |
| − | TEXT= | + | $\text{Beispiel 2:}$ Wir betrachten die Verbundwahrscheinlichkeiten $P_{RS}(·)$ unseres Würfelexperiments, die im [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|letzten Kapitel]] als |$\text{Beispiel 6}$] ermittelt wurden. In der Mitte der folgenden Grafik ist $P_{RS}(·)$ nochmals angegeben. |
| − | [[Datei:P_ID2764__Inf_T_3_2_S3.png|frame| | + | [[Datei:P_ID2764__Inf_T_3_2_S3.png|center|frame|Verbundwahrscheinlichkeiten $P_{RS}$ und bedingte Wahrscheinlichkeiten $P_{S \vert R}$ und $P_{R \vert S}$]] |
Außen sind die beiden bedingten Wahrscheinlichkeitsfunktionen gezeichnet: | Außen sind die beiden bedingten Wahrscheinlichkeitsfunktionen gezeichnet: | ||
Version vom 22. April 2018, 13:46 Uhr
Inhaltsverzeichnis
Definition der Entropie unter Verwendung von supp(PXY)
Wir fassen die Ergebnisse des letzten Kapitels nochmals kurz zusammen, wobei wir von der zweidimensionalen Zufallsgröße $XY$ mit der Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$ ausgehen. Gleichzeitig verwenden wir die Schreibweise
- $${\rm supp} (P_{XY}) = \big \{ \hspace{0.05cm}(x, y) \in XY \hspace{0.05cm}, \hspace{0.3cm} {\rm wobei} \hspace{0.15cm} P_{XY}(X, Y) \ne 0 \hspace{0.05cm} \big \} \hspace{0.05cm};$$
$\text{Zusammenfassende Darstrellung:}$ Mit dieser Teilmenge $\text{supp}(P_{XY}) ⊂ P_{XY}$ gilt für
- die Verbundentropie (englisch: Joint Entropy):
- $$H(XY) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.05cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(x, y)} \hspace{0.05cm}.$$
- die Entropien der 1D–Zufallsgrößen $X$ und $Y$:
- $$H(X) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ] =\hspace{-0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{X})} \hspace{-0.2cm} P_{X}(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(x)} \hspace{0.05cm},$$
- $$H(Y) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(Y)}\right ] =\hspace{-0.2cm} \sum_{y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Y})} \hspace{-0.2cm} P_{Y}(y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(y)} \hspace{0.05cm}.$$
$\text{Beispiel 1:}$ Wir beziehen uns nochmals auf die Beispiele auf der Seite Verbundwahrscheinlichkeit und Verbundentropie im letzten Kapitel.
Bei der 2D–Wahrscheinlichkeitsfunktion $P_{RB}(R, B)$ im dortigen $\text{Beispiel 5}$ mit den Parametern
- $R$ ⇒ Augenzahl des roten Würfels und
- $B$ ⇒ Augenzahl des blauen Würfels
sind die Mengen $P_{RB}$ und $\text{supp}(P_{RB})$ identisch. Hier sind alle $6^2 = 36$ Felder mit Werten ungleich Null belegt.
Bei der 2D Wahrscheinlichkeitsfunktion $P_{RS}(R, S)$ im $\text{Beispiel 6}$ mit den Parametern
- $R$ ⇒ Augenzahl des roten Würfels und
- $S = R + B$ ⇒ Summe der beiden Würfel
gibt es $6 · 11 = 66$ Felder, von denen allerdings viele leer sind, also für die Wahrscheinlichkeit „0” stehen.
- Die Teilmenge $\text{supp}(P_{RS})$ beinhaltet dagegen nur die 36 schraffierten Felder mit von Null verschiedenen Wahrscheinlichkeiten.
- Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da für $x → 0$ der Grenzwert $x · \log_2 ({1}/{x}) = 0$ ist.
Bedingte Wahrscheinlichkeit und bedingte Entropie
Im Buch „Stochastische Signaltheorie” wurden für den Fall zweier Ereignisse $X$ und $Y$ die folgenden bedingten Wahrscheinlichkeiten angegeben ⇒ Satz von Bayes:
- $${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} {\rm Pr} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (X)} \hspace{0.05cm}.$$
Angewendet auf Wahrscheinlichkeitsfunktionen erhält man somit:
- $$P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{P_{XY}(X, Y)}{P_{Y}(Y)} \hspace{0.05cm}, \hspace{0.5cm} P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{P_{XY}(X, Y)}{P_{X}(X)} \hspace{0.05cm}.$$
Analog zur Verbundentropie $H(XY)$ lassen sich hier folgende Entropiefunktionen ableiten:
$\text{Definitionen:}$
Die bedingte Entropie (englisch: Conditional Entropy) der Zufallsgröße $X$ unter der Bedingung $Y$ lautet:
- $$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{Y}(y)}{P_{XY}(x, y)} \hspace{0.05cm}.$$
In gleicher Weise erhält man für die zweite bedingte Entropie:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} \hspace{0.05cm}.$$
Im Argument der Logarithmusfunktion steht stets eine bedingte Wahrscheinlichkeitsfunktion ⇒ $P_{X\hspace{0.03cm}| \hspace{0.03cm}Y}(·)$ bzw. $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(·)$, während zur Erwartungswertbildung die Verbundwahrscheinlichkeit ⇒ $P_{XY}(·)$ benötigt wird.
Für die bedingten Entropien gibt es folgende Begrenzungen:
- Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich Null. Aus $H(X|Y) = 0$ folgt direkt auch $H(Y|X) = 0$. Beides ist nur für disjunkte Mengen $X$ und $Y$ möglich.
- Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese Aussage ist einleuchtend, wenn man sich bewusst macht, dass man für „Entropie” synonym auch „Unsicherheit” verwenden kann.
- Denn: Die Unsicherheit bezüglich der Menge $X$ kann nicht dadurch größer werden, dass man $Y$ kennt. Außer bei statistischer Unabhängigkeit ⇒ $H(X|Y) = H(X)$ gilt stets $H(X|Y) < H(X)$.
- Wegen $H(X) ≤ H(XY)$, $H(Y) ≤ H(XY)$ gilt somit auch $H(X|Y) ≤ H(XY)$ und $H(Y|X) ≤ H(XY)$. Eine bedingte Entropie kann also nie größer werden als die Verbundentropie.
$\text{Beispiel 2:}$ Wir betrachten die Verbundwahrscheinlichkeiten $P_{RS}(·)$ unseres Würfelexperiments, die im letzten Kapitel als
Transinformation zwischen zwei Zufallsgrößen
Wir betrachten die Zufallsgröße $XY$ mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$. Bekannt seien auch die 1D–Funktionen $P_X(X)$ und $P_Y(Y)$. Nun stellen sich folgende Fragen:
- Wie vermindert die Kenntnis der Zufallsgröße $Y$ die Unsicherheit bezüglich $X$?
- Wie vermindert die Kenntnis der Zufallsgröße $X$ die Unsicherheit bezüglich $Y$?
Zur Beantwortung benötigen wir eine für die Informationstheorie substantielle Definition:
Definition: Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $X$ und $Y$ – beide über dem gleichen Alphabet – ist gegeben durch den Ausdruck
- $$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] =\hspace{-0.25cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(x, y)} {P_{X}(x) \cdot P_{Y}(y) } \hspace{0.01cm}.$$
Ein Vergleich mit demletzten Kapitel zeigt, dass die Transinformation auch als Kullback–Leibler–Distanz zwischen der 2D–PMF $P_{XY}(⋅)$ und dem Produkt $P_X(⋅) · P_Y(⋅)$ geschrieben werden kann:
- $$I(X;Y) = D(P_{XY} \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_X \cdot P_Y) \hspace{0.05cm}.$$
Es ist offensichtlich, dass stets $I(X; Y)$ ≥ 0 gilt. Wegen der Symmetrie ist auch $I(Y; X)$ = $I(X; Y)$.
Sucht man in einem Wörterbuch die Übersetzung für „mutual”, so findet man unter Anderem die Begriffe „gemeinsam”, „gegenseitig”, „beidseitig” und „wechselseitig”. Und ebenso sind in Fachbüchern für $I(X; Y)$ auch die Bezeichnungen gemeinsame Entropie und gegenseitige Entropie üblich. Wir sprechen aber im Folgenden durchgängig von der Transinformation $I(X; Y)$ und interpretieren nun diese Größe:
- Durch Aufspalten des $log_2$–Arguments entsprechend
- $$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac{1} {P_{X}(X) }\right ] - {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac {P_{Y}(Y) }{P_{XY}(X, Y)} \right ] $$
- erhält man unter Verwendung von $P_{X|Y}(⋅) = P_{XY}(⋅)/P_Y(Y)$:
- $$I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) \hspace{0.05cm}.$$
- Das heißt: Die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ vermindert sich bei Kenntnis von $Y$ um den Betrag $H(X|Y)$. Der Rest ist die Transinformation $I(X; Y)$.
- Bei anderer Aufspaltung kommt man zum Ergebnis $I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$
Ergo: Die Transinformation $I(X; Y)$ ist symmetrisch ⇒ $X$ sagt genau so viel über $Y$ aus wie $Y$ über $X$ ⇒ gegenseitige Information. Das Semikolon weist auf die Gleichberechtigung hin.
Oft werden die hier genannten Gleichungen durch ein Schaubild verdeutlicht, so auch in den folgenden Beispielen. Daraus erkennt man, dass auch folgende Gleichungen zutreffen:
- $$I(X;Y) = H(X) + H(Y) - H(XY) \hspace{0.05cm},$$
- $$I(X;Y) = H(XY) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$
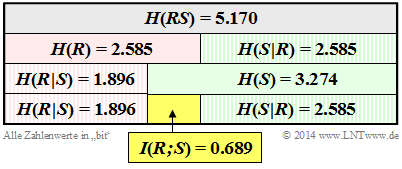
Beispiel 3: Wir kommen nochmals auf das Würfel–Experiment mit dem roten $(R)$ und dem blauen $(B)$ Würfel zurück. Die Zufallsgröße $S$ gibt die Summe der beiden Würfel an: $S = R + B$. Wir betrachten hier die 2D–Zufallsgröße RS. In früheren Beispielen haben wir berechnet:
- die Entropien $H(R) = 2.585 \ \rm bit$ und $H(S) = 3.274 \ \rm bit$ ⇒ Beispiel 5 im letzten Kapitel,
- die Verbundentropie $H(RS) = 5.170 \ \rm bit$ ⇒ Beispiel 5 im letzten Kapitel,
- die bedingten Entropien $H(S \vert R) = 2.585 \ \rm bit$ und $H(R \vert S) = 1.896 \ \rm bit$ ⇒ Beispiel 2 im letztenAbschnitt.
Diese Größen sind in der Grafik zusammengestellt, wobei die Zufallsgröße $R$ durch die Grundfarbe „Rot” und die Summe $S$ durch die Grundfarbe „grün” markiert sind. Bedingte Entropien sind schraffiert. Man erkennt aus dieser Darstellung:
- Hier ist $H(R) = \log_2 (6) = 2.585\ \rm bit$ genau halb so groß wie die Verbundentropie $H(RS)$. Kennt man $R$, so liefert $S$ genau die gleiche Information wie die Zufallsgröße $B$, nämlich $H(S \vert R) = H(B) = \log_2 (6) = 2.585\ \rm bit$. Hinweis: $H(R)$ = $H(S \vert R)$ gilt nicht allgemein.
- Die Entropie $H(S) = 3.274 \ \rm bit$ ist im vorliegenden Beispiel erwartungsgemäß größer als $H(R)$. Wegen $H(S) + H(R \vert S) = H(R) + H(S \vert R)$ muss deshalb $H(R \vert S)$ gegenüber $H(S \vert R)$ um den gleichen Betrag $I(R; S) = 0.689 \ \rm bit$ kleiner sein wie $H(R)$ gegenüber $H(S)$.
- Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $R$ und $S$ ergibt sich aber auch aus der Gleichung
- $$I(R;S) = H(R) + H(S) - H(RS) = 2.585\,{\rm bit} + 3.274\,{\rm bit} - 5.170\,{\rm bit} = 0.689\,{\rm bit} \hspace{0.05cm}. $$
Bedingte Transinformation
Wir betrachten nun drei Zufallsgrößen $X$, $Y$ und $Z$, die zueinander in Beziehung stehen (können).
Definition: Die bedingte Transinformation (englisch: Conditional Mutual Information) zwischen den Zufallsgrößen $X$ und $Y$ bei gegebenem $Z = z$ lautet:
- $$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z = z) - H(X\vert\hspace{0.05cm}Y ,\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$
Dagegen bezeichnet man als die bedingte Transinformation zwischen den Zufallsgrößen $X$ und $Y$ bei gegebener Zufallsgröße Z:
- $$I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z ) = H(X\hspace{0.05cm}\vert\hspace{0.05cm} Z ) - H(X\vert\hspace{0.05cm}Y Z )= \hspace{-0.3cm} \sum_{z \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Z})} \hspace{-0.25cm} P_{Z}(z) \cdot I(X;Y \hspace{0.05cm}\vert\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$
Hierbei ist $P_Z(Z)$ die Wahrscheinlichkeitsfunktion der neben $X$ und $Y$ betrachteten Zufallsgröße $Z$ und $P_Z(z)$ die Wahrscheinlichkeit für $Z = z$.
Bitte beachten Sie: Für die bedingte Entropie gilt bekanntlich die Größenrelation $H(X|Z) ≤ H(X)$. Für die Transinformation gilt diese Größenrelation nicht unbedingt: $I(X; Y|Z)$ kann kleiner, gleich, aber auch größer sein als $I(X; Y)$.
Beispiel 3:
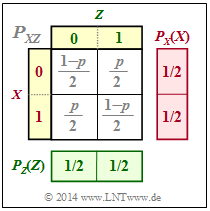
Wir betrachten die binären Zufallsgrößen $X$, $Y$ und $Z$ mit folgenden Eigenschaften:
- $X$ und $Y$ seien statistisch unabhängig.
- Für ihre Wahrscheinlichkeitsfunktionen gelte: $P_X(X) = [1/2, 1/2]$, $P_Y(Y) = [1– p, p]$ ⇒ $H(X) = 1$, $H(Y) = H_{\rm bin}(p)$.
- $Z$ ist die Modulo–2–Summe von $X$ und $Y$: $Z = X ⊕ Y$.
Aus der Verbund–PMF $P_{XZ}$ gemäß der oberen Grafik folgt:
- Durch Summation der Spalten–Wahrscheinlichkeiten ergibt sich $P_Z(Z) = [1/2; 1/2]$ ⇒ $H(Z) = 1$.
- $X$ und $Z$ sind ebenfalls statistisch unabhängig, da für die 2D–PMF $P_{XZ}(X, Z) = P_X(X) · P_Z(Z)$ gilt.
- Daraus folgt: $H(Z\vert X) = H(Z)$, $H(X \vert Z) = H(X)$, $I(X; Z) = 0$.
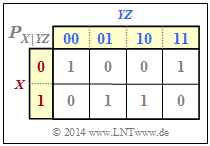
Aus der bedingten Wahrscheinlichkeitsfunktion $P_{X\vert YZ}$ gemäß der unteren Grafik lassen sich berechnen:
- $H(X\vert YZ)$ = 0, da alle $P_{X\vert YZ}$–Einträge entweder $0$ oder $1$ sind ⇒ bedingte Entropie,
- $I(X; YZ)$ = $H(X)$ – $H(X\vert YZ)$ = $H(X)$ ⇒ Transinformation,
- $I(X; Y\vert Z)$ = $H(X\vert Z)$ = $H(X)$ ⇒ bedingte Transinformation.
Im vorliegenden Beispiel ist also $I(X; Y\vert Z) = 1$ größer als $I(X; Y) = 0$. Hinweis:In diesem Beispiel müssten noch alle (bedingte) Entropien und auch die (bedingte) Transinformation mit der Pseudo-Einheit „bir” versehen werden.
Kettenregel der Transinformation
Bisher haben wir die Transinformation nur zwischen zwei eindimensionalen Zufallsgrößen betrachtet. Nun erweitern wir die Definition auf insgesamt $n + 1$ Zufallsgrößen, die wir aus Darstellungsgründen mit $X_1$, ... , $X_n$ sowie $Z$ bezeichnen. Dann gilt:
Kettenregel der Transinformation: Die Transinformation zwischen der $n$–dimensionalen Zufallsgröße $X_1 X_2 ... X_n$ und der Zufallsgröße $Z$ lässt sich wie folgt darstellen und berechnen:
$$I(X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_n;Z) = I(X_1;Z) + I(X_2;Z \vert X_1) + ... \hspace{0.1cm}+ I(X_n;Z\vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_{n-1}) = \sum_{i = 1}^{n} I(X_i;Z \vert X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_{i-1}) \hspace{0.05cm}.$$
Beweis: Hier beschränken wir uns auf den Fall $n = 2$, also auf insgesamt drei Zufallsgrößen, und ersetzen $X_1$ durch $X$ und $X_2$ durch $Y$. Dann erhalten wir:
- $$\begin{align*}I(X\hspace{0.05cm}Y;Z) & = H(XY) - H(XY \vert Z) = \\ & = \big [ H(X)+ H(Y\vert X)\big ] - \big [ H(X\vert Z) + H(Y\vert XZ)\big ] =\\ & = \big [ H(X)- H(X\vert Z)\big ] - \big [ H(Y\vert X) + H(Y\vert XZ)\big ]=\\ & = I(X;Z) + I(Y;Z \vert X) \hspace{0.05cm}.\end{align*}$$
Aus dieser Gleichung erkennt man, dass die die Größenrelation $I(X Y; Z) ≥ I(X; Z)$ immer gegeben ist. Gleichheit ergibt sich für die bedingte Transinformation $I(Y; Z\vert X) = 0$, also dann, wenn die Zufallsgrößen $Y$ und $Z$ für ein gegebenes $X$ statistisch unabhängig sind.
Beispiel 4: Wir betrachten die Markovkette $X → Y → Z$. Für eine solche Konstellation gilt stets das Data Processing Theorem mit der folgenden Konsequenz, die sich aus der Kettenregel der Transinformation ableiten lässt:
- $$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm}I(X;Y ) \hspace{0.05cm},$$
- $$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm} I(Y;Z ) \hspace{0.05cm}.$$
Das Theorem besagt somit:
- Man kann durch Manipulation (Processing $Z$) der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
- Die Datenverarbeitung $Y → Z$ (durch einen zweiten Prozessor) dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.
Weitere Informationen zum Data Processing Theorem finden Sie in der Aufgabe 3.15.
Aufgaben zum Kapitel
Aufgabe 3.7: Einige Entropieberechnungen
Aufgabe 3.8: Nochmals Transinformation
Aufgabe 3.8Z: Tupel aus ternären Zufallsgrößen
Aufgabe 3.9: Bedingte Transinformation