Aufgaben:Aufgabe 3.2: G–Matrix eines Faltungscodierers

• Zurück zum Buch

Vorgegebener Faltungscodierer

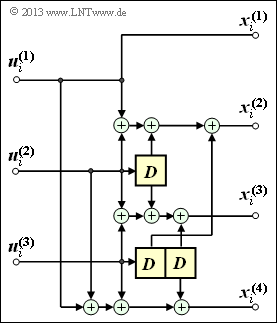
Wir betrachten wie in Aufgabe 3.1 den nebenstehend gezeichneten Faltungscodierer der Rate $3/4$. Dieser wird durch den folgenden Gleichungssatz charakterisiert:

$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$

$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$

$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$

$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}\hspace{0.05cm}.$$

Bezieht man sich auf die bei $i = 1$ beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen

$$\underline{\it u} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it u}_1, \underline{\it u}_2, \text{...} \hspace{0.1cm}, \underline{\it u}_i ,\text{...} \hspace{0.1cm} \right )\hspace{0.05cm},$$

$$\underline{\it x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left ( \underline{\it x}_1, \underline{\it x}_2, \text{...} \hspace{0.1cm}, \underline{\it x}_i , \text{...} \hspace{0.1cm} \right )$$

mit $\underline{u}_i = (u_i^{(1)}, u_i^{(2)}, \ \text{...} \ , u_i^{(k)})$ bzw. $\underline{x}_i = (x_i^{(1)}, x_i^{(2)}, \ \text{...} \ , x_i^{(n)})$, so kann der Zusammenhang zwischen der Informationssequenz $\underline{u}$ und der Codesequenz $\underline{x}$ durch die Generatormatrix $\mathbf{G}$ in folgender Form ausgedrückt werden:

$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$

Für die Generatormatrix eines Faltungscoders mit dem Gedächtnis $m$ ist dabei zu setzen:

$${ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \ddots & \ddots & & & \ddots \end{pmatrix}\hspace{0.05cm}.$$

Hierbei bezeichnen $\mathbf{G}_0, \mathbf{G}_1, \mathbf{G}_2, \ \text{...}$ Teilmatrizen mit jeweils $k$ Zeilen und $n$ Spalten sowie binären Matrixelementen ($0$ oder $1$). Ist das Matrixelement $\mathbf{G}_l(\kappa, j) = 1$, so bedeutet dies, dass das Codebit $x_i^{(j)}$ durch das Informationsbit $u_{i-l}^{(\kappa)}$ beeinflusst wird. Andernfalls ist dieses Matrixelement gleich $0$.

Ziel dieser Aufgabe ist es, die zur Informationssequenz

$$\underline{u} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm} ,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})$$

gehörige Codesequenz $\underline{x}$ entsprechend den obigen Vorgaben zu berechnen. Das Ergebnis müsste mit dem Ergebnis von Aufgabe 3.1 übereinstimmen, das allerdings auf anderem Wege erzielt wurde.

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels Algebraische und polynomische Beschreibung.

Fragebogen

1

Aus wie vielen Teilmatrizen $\mathbf{G}_l$ setzt sich die Matrix $\mathbf{G}$ zusammen?

${\rm Anzahl \ der \ Teilmatrizen} \ = \ $

2

Welche Aussagen treffen für die Teilmatrix $\mathbf{G}_0$ zu?

	Insgesamt beinhaltet $\mathbf{G}_0$ acht Einsen.
	Die erste Zeile von $\mathbf{G}_0$ lautet $1 \ 1 \ 0 \ 1$.
	Die erste Zeile von $\mathbf{G}_0$ lautet $1 \ 0 \ 0$.

3

Welche aussagen treffen für die Teilmatrix $\mathbf{G}_1$ zu?

	Die erste Zeile lautet $0 \ 0 \ 0 \ 0$.
	Die zweite Zeile lautet $0 \ 1 \ 1 \ 0$.
	Die dritte Zeile lautet $0 \ 1 \ 0 \ 0$.

4

Ermitteln Sie die ersten neun Zeilen und zwölf Spalten der Generatormatrix $\mathbf{G}$. Welche Aussagen treffen zu?

	Es gibt mindestens eine Zeile mit lauter Nullen.
	Es gibt mindestens eine Zeile mit lauter Einsen.
	In den Spalten $1, 5, 9$ steht jeweils nur eine einzige Eins.

5

Welche Codesequenz $\underline {x}$ ergibt sich für $\underline {u} = (0, 1, 1, 1, 1, 0, 1, 0, 1)$?

	Es gilt: $\underline{x} = (1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, \ \text{...})$.
	Es gilt: $\underline{x} = (0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, \ \text{...})$.
	Es gilt: $\underline{x} = (0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, \ \text{...})$.

Musterlösung

Musterlösung

(1)  Das Gedächtnis des betrachteten Faltungscodierers ist $m = 2$. Damit setzt sich die Generatormatrix $\mathbf{G}$ aus den $m + 1 \ \underline {= 3}$ Teilmatrizen $\mathbf{G}_0, \mathbf{G}_1$ und $\mathbf{G}_2$ zusammen.

(2)  Richtigsind die u>Aussage 1 und 2:

• Aus den angegebenen Gleichungen

$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} \hspace{0.05cm},$$

$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i-1}^{(2)} + u_{i-1}^{(3)} \hspace{0.05cm},$$

$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-1}^{(2)} + u_{i-2}^{(3)} \hspace{0.05cm},$$

$$x_i^{(4)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)} + u_{i}^{(3)}+ u_{i-2}^{(3)}$$

erkennt man, dass im gesamten Gleichungssatz genau achtmal ein Eingangswert $u_i^{(j)}$ mit $j ∈ \{1, 2, 3\}$ vorkommt   ⇒   Aussage 1 trifft zu.

• Der Eingangswert $u_i^{(1)}$ beeinflusst die Ausgänge $x_i^{(1)}$, $x_i^{(2)}$ und $x_i^{(4)}$. Damit lautet die erste Zeile von $\mathbf{G}_0 \text{:} \, 1 \ 1 \ 0 \ 1$   ⇒   auch Aussage 2 trifft zu.
• Dagegen ist die Aussage 3 falsch: Nicht die erste Zeile von $\mathbf{G}_0$ lautet $1 \ 0 \ 0$, sondern die erste Spalte. Dies besagt, dass $x_i^{(1)}$ nur von $u_i^{(1)}$ abhängt, aber nicht von $u_i^{(2)}$ oder von $u_i^{(3)}$. Es handelt sich um einen systematischen Code.

(3)  Alle Aussagen sind zutreffend:

• Im Gleichungssatz kommt dreimal ein Eingangswert $u_{i–1}^{(j)}$ mit $j ∈ \{1, 2, 3\}$ vor. Somit beinhaltet $\mathbf{G}_1$ insgesamt drei Einsen.
• Der Eingangswert $u_{i-1}^{(2)}$ beeinflusst die Ausgänge $x_i^{(2)}$ und $x_i^{(3)}$, während $u_{i-1}^{(3)}$ nur für die Berechnung von $x_i^{(2)}$ herangezogen wird.

(4)  Richtig ist nur die Aussage 3:

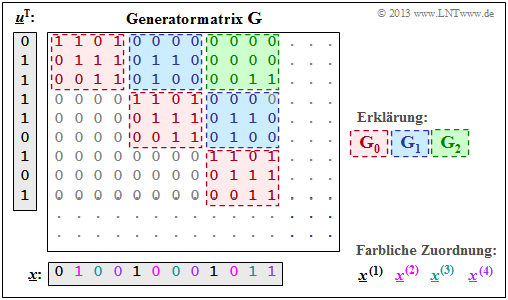
• Die folgende Grafik zeigt den linken oberen Beginn (die Zeilen 1 bis 9 sowie die Spalten 1 bis 12) der Generatormatrix $\mathbf{G}$.
• Daraus ist ersichtlich, dass die beiden ersten Aussagen falsch sind .
• Dieses Ergebnis gilt für jeden systematischen Code mit den Parametern $k = 3$ und $n = 4$.

Generatormatrix eines Faltungscodes: $k = 4, \ n = 4, \ m = 2$

(5)  Richtig ist die Aussage 2:

• Allgemein gilt $\underline{x} = \underline{u} \cdot \mathbf{G}$, wobei $\underline{u}$ und $\underline{x}$ Sequenzen sind, das heißt, dass sie sich bis ins Unendliche fortsetzen. Entsprechend ist die Generatormatrix $\mathbf{G}$ weder nach unten noch nach rechts begrenzt.
• Bei begrenzter Informationssequenz $\underline{u}$ (hier auf $9$ Bit) ist auch die Codesequenz $\underline{x}$ begrenzt.
• Interessiert man sich nur für die ersten Bits, so genügt es, nur den linken oberen Ausschnitt der Generatormatrix wie in der Musterlösung zur Teilaufgabe (4) zu betrachten.
• Anhand dieser Grafik kann auch das Ergebnis der Matrizengleichung $\underline{x} = \underline{u} \cdot \mathbf{G}$ abgelesen werden. Richtig ist $\underline{x} = (0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, \ ...)$ und damit Antwort 2.

Das gleiche Ergebnis haben wir in der Teilaufgabe (4) von Aufgabe 3.1 erhalten.

• Dargestellt sind hier nur $9$ Informationsbits und $9 \cdot n/k = 12$ Codebits. Aufgrund der Teilmatrizen $\mathbf{G}_1$ und $\mathbf{G}_2$ würden sich hier aber auch die Codebits 13 bis 20 noch (teilweise) Einsen ergeben.

• Die Codesequenz $\underline{x}$ setzt sich aus den vier Teilsequenzen $\underline{x}^{(1)}, \ \text{...} \ , \ \underline{x}^{(4)}$ zusammen, die in der Grafik aufgrund unterschiedlicher Farbgebung abgelesen werden können.