Kanalcodierung/Kanalmodelle und Entscheiderstrukturen

1. Kanalcodierung
2. Binäre Blockcodes zur Kanalcodierung
3. Kanalmodelle und Entscheiderstrukturen

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

AWGN–Kanal bei binärem Eingang

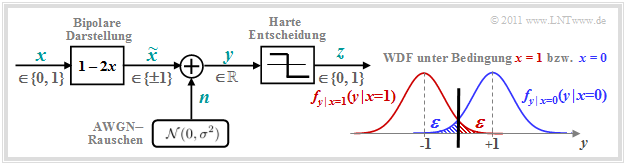
Wir betrachten das bekannte zeitdiskrete AWGN–Kanalmodell gemäß der unteren linken Grafik:

• Das binäre und zeitdiskrete Nachrichtensignal $x$ nimmt mit gleicher Wahrscheinlichkeit die Werte $0$ und $1$ an, das heißt, es ist ${\rm Pr}(x = 0) = {\rm Pr}(\tilde{x} =+1) = 1/2$ sowie ${\rm Pr}(x = 1) = {\rm Pr}(\tilde{x} =-1) = 1/2$.
  

• Die Übertragung wird durch additives weißes gaußverteiltes Rauschen (AWGN) $n$ mit der (normierten) Rauschleistung $\sigma^2 = N_0/E_{\rm B}$ beeinträchtigt. Die Streuung der Gauß–WDF ist $\sigma$.
  

• Aufgrund der Gaußschen WDF kann das Ausgangssignal $y = \tilde{x} +n$ alle reellen Werte im Bereich von $-\infty$ bis $+\infty$ annehmen. Der Signalwert $y$  ist demzufolge zwar wie $x$ (bzw. $\tilde{x})$ zeitdiskret, im Gegensatz zu diesem aber wertkontinuierlich.
  

Modell und WDF des AWGN–Kanals

Die rechte Grafik zeigt die bedingten Wahrscheinlichkeitsdichtefunktionen (in blau bzw. rot):

\[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=0 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=0 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e}^{ - (y-1)^2/(2\sigma^2) }\hspace{0.05cm},\]

\[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e}^{ - (y+1)^2/(2\sigma^2) }\hspace{0.05cm}.\]

Nicht dargestellt ist die gesamte (unbedingte) WDF, für die bei gleichwahrscheinlichen Symbolen gilt:

\[f_y(y) = {1}/{2} \cdot \left [ f_{y \hspace{0.03cm}| \hspace{0.03cm}x=0 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=0 ) + f_{y \hspace{0.03cm}| \hspace{0.03cm}x=1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=1 )\right ]\hspace{0.05cm}.\]

Die beiden schraffierten Flächeninhalte (jeweils $\varepsilon$) markieren Entscheidungsfehler unter der Voraussetzung $x=0$   ⇒   $\tilde{x} = +1$ (blau)   bzw. $x=1$   ⇒   $\tilde{x} = -1$ (rot), wenn harte Entscheidungen getroffen werden:

\[z = \left\{ \begin{array}{c} 0\\ 1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls} \hspace{0.15cm} y > 0\hspace{0.05cm},\\ {\rm falls} \hspace{0.15cm}y < 0\hspace{0.05cm}.\\ \end{array}\]

Bei gleichwahrscheinlichen Eingangssymbolen ist dann die mittlere Bitfehlerwahrscheinlichkeit ${\rm Pr}(z \ne x)$ ebenfalls gleich $\varepsilon$. Mit dem komplementären Gaußschen Fehlerintergral ${\rm Q}(x)$ gilt dabei:

\[\varepsilon = {\rm Q}(1/\sigma) = {\rm Q}(\sqrt{\rho}) = \frac {1}{\sqrt{2\pi} } \cdot \int_{\sqrt{\rho}}^{\infty}{\rm e}^{- \alpha^2/2} \hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.\]

Hierbei bezeichnet $\rho = 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$ das Signal–zu–Rauschverhältnis (SNR) vor dem Entscheider, wobei folgende Systemgrößen verwendet werden:

• $E_{\rm S}$ ist die Signalenergie pro Symbol (ohne Codierung gleich $E_{\rm B}$, also gleich der Signalenergie pro Bit),
  

• $N_0$ bezeichnet die konstante (einseitige) Rauschleistungsdichte des AWGN–Kanals.
  
  

Hinweis:  Der dargelegte Sachverhalt wird mit dem interaktiven Applet Symbolfehlerwahrscheinlichkeit von Digitalsystemen verdeutlicht.

Binary Symmetric Channel – BSC

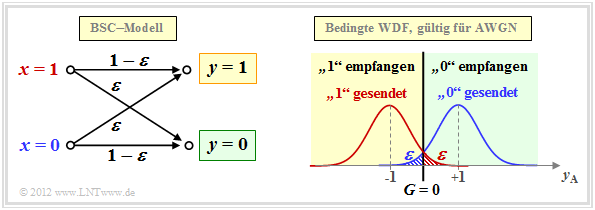
Das AWGN–Kanalmodell ist kein digitales Kanalmodell, wie wir es im Abscnitt Blockschaltbild und Voraussetzungen zur einführenden Beschreibung der Kanalcodierverfahren vorausgesetzt haben. Berücksichtigen wir aber eine harte Entscheidung, so kommen wir zum digitalen Modell Binary Symmetric Channel (BSC):

BSC–Modell und Zusammenhang mit dem AWGN–Modell

Wählt man die Verfälschungswahrscheinlichkeiten ${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x=0)$ bzw. ${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x=1)$ jeweils zu

\[\varepsilon = {\rm Q}(\sqrt{\rho})\hspace{0.05cm},\]

so ist der Zusammenhang zum AWGN–Kanalmodell hergestellt. Die Entscheidungsgrenze liegt dabei bei $G = 0$, wodurch auch die Eigenschaft „symmetrisch” begründet ist.

Hinweis:  Beim AWGN–Modell haben wir die binäre Ausgangsgröße (nach Schwellenwertentscheidung) mit $z \in \{0, \hspace{0.05cm}1\}$ bezeichnet. Bei den digitalen Kanalmodellen (BSC, BEC, BSEC) bezeichnen wir nun den wertdiskreten Ausgang wieder mit $y$. Um Verwechslungen zu vermeiden, nennen wir das Ausgangssignal des AWGN–Modells nun $y_{\rm A}$. Für das analoge Empfangssignal gilt $y_{\rm A} = \tilde{x} +n$.

Das BSC–Modell liefert eine statistisch unabhängige Fehlerfolge und eignet sich somit zur Modellierung gedächtnisloser rückkopplungsfreier Kanäle, die in diesem Buch ausnahmslos betrachtet werden.

Zur Beschreibung gedächtnisbehafteter Kanäle müssen andere Modelle herangezogen werden, die im fünften Hauptkapitel des Buches „Digitalsignalübertragung” behandelt werden, zum Beispiel Bündelfehlerkanäle nach

• dem Gilbert–Elliott–Modell,
  

• dem McCullough–Modell.
  
  

Statistisch unabhängige Fehler (links) und Bündelfehler (rechts)

$\text{Beispiel 1:}$  Die Abbildung zeigt

• statistisch unabhängige Fehler nach dem BSC–Modell (links), und
• so genannte Bündelfehler gemäß Gilbert–Elliott (rechts).

Die Bitfehlerrate beträgt in beiden Fällen $10\%$. Aus der rechten Grafik ist zu erkennen, dass das Bild zeilenweise übertragen wird.

Binary Erasure Channel – BEC

Das BSC–Modell liefert nur die Aussagen „richtig” und „falsch”. Manche Empfänger – so zum Beispiel die so genannten Soft–in Soft–out Decoder – können jedoch auch gewisse Informationen über die Sicherheit der Entscheidung liefern, wobei sie natürlich darüber informiert werden müssen, welche ihrer Eingangswerte sicher sind und welche eher unsicher.

Binary Erasure Channel (BEC) und Zusammenhang mit dem AWGN–Modell

Der Binary Erasure Channel (BEC) liefert eine solche Information. Anhand der Grafik erkennt man:

• Das Eingangsalphabet des BEC–Kanalmodells ist binär   ⇒   $x ∈ \{0, \hspace{0.05cm}1\}$ und das Ausgangsalphabet ternär   ⇒   $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$. Ein $\rm E$ kennzeichnet eine unsichere Entscheidung. Dieses neue „Symbol” steht für Erasure, zu deutsch: Auslöschung.

• Bitfehler werden durch das BEC–Modell per se ausgeschlossen. Eine unsichere Entscheidung $\rm (E)$ wird mit der Wahrscheinlichkeit $\lambda$ getroffen, während die Wahrscheinlichkeit für eine richtige (und gleichzeitig sichere) Entscheidung $1-\lambda$ beträgt.

• Rechts oben ist der Zusammenhang zwischen BEC– und AWGN–Kanalmodell dargestellt, wobei das Erasure–Entscheidungsgebiet $\rm (E)$ grau hinterlegt ist. Im Gegensatz zum BSC–Modell gibt es nun zwei Entscheidungsgrenzen $G_0 = G$  und  $G_1 = -G$ gibt. Es gilt:

\[\lambda = {\rm Q}[\sqrt{\rho} \cdot (1 - G)]\hspace{0.05cm}.\]

Wir weisen hier nochmals auf die folgenden Applets hin:

• Symbolfehlerwahrscheinlichkeit von Digitalsystemen,
• Komplementäre Gaußsche Fehlerfunktion.

Binary Symmetric Error & Erasure Channel – BSEC

Das BEC–Modell ist aufgrund der Fehlerwahrscheinlichkeit $0$ eher unrealistisch und nur eine Näherung für ein extrem großes Signal–zu–Rausch–Leistungsverhältnis (kurz SNR) $\rho$.

Stärkere Störungen   ⇒   ein kleineres $\rho$ sollten besser durch den Binary Symmetric Error & Erasure Channel (BSEC) mit den zwei Parametern

• Verfälschungswahrscheinlichkeit   $\varepsilon = {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x=0)= {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x=1)$,
  

• Erasure–Wahrscheinlichkeit   $\lambda = {\rm Pr}(y = {\rm E}\hspace{0.05cm}|\hspace{0.05cm} x=0)= {\rm Pr}(y = {\rm E}\hspace{0.05cm}|\hspace{0.05cm} x=1)$

modelliert werden. Wie beim BEC–Modell gilt auch hier $x ∈ \{0, \hspace{0.05cm}1\}$  und  $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$.

Binary Symmetric Error & Erasure Channel (BSEC) & Zusammenhang mit dem AWGN–Modell

$\text{Beispiel 2:}$  Wir betrachten das BSEC–Modell mit den beiden Entscheidungsgeraden $G_0 = G = 0.5$ und $G_1 = -G = -0.5$ , dessen Parameter $\varepsilon$ und $\lambda$ durch das SNR $\rho=1/\sigma^2$ des vergleichbaren AWGN–Kanals festgelegt sind. Dann gilt

• für $\sigma = 0.5$   ⇒   $\rho = 4$:

\[\varepsilon = {\rm Q}\big[\sqrt{\rho} \cdot (1 + G)\big] = {\rm Q}(3) \approx 0.14\%\hspace{0.05cm},\hspace{0.6cm} {\it \lambda} = {\rm Q}\big[\sqrt{\rho} \cdot (1 - G)\big] - \varepsilon = {\rm Q}(1) - {\rm Q}(3) \approx 15.87\% - 0.14\% = 15.73\%\hspace{0.05cm},\]

• für $\sigma = 0.25$   ⇒   $\rho = 16$:

\[\varepsilon = {\rm Q}(6) \approx 10^{-10}\hspace{0.05cm},\hspace{0.6cm} {\it \lambda} = {\rm Q}(2) \approx 2.27\%\hspace{0.05cm}.\]

Für die rechts dargestellte WDF wurde $\rho = 4$ vorausgesetzt. Für$\rho = 16$ könnte das BSEC–Modell durch die einfachere BEC–Variante ersetzt werden, ohne dass es zu gravierenden Unterschieden kommt.

Maximum-a-posteriori– und Maximum-Likelihood–Kriterium

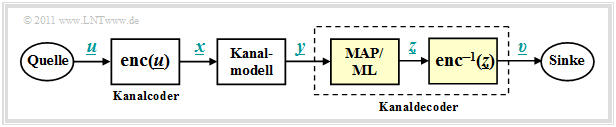
Wir gehen nun von dem nachfolgend skizzierten Modell aus und wenden die bereits im Kapitel Struktur des optimalen Empfängers des Buches „Digitalsignalübertragung” genannten Entscheidungskriterien auf den Decodiervorgang an.

Modell zur Beschreibung von MAP– und ML–Decodierung

Aufgabe des Kanaldecodierers ( oder Kanaldecoders) ist es, den Ausgabevektor $\underline{v}$  so zu bestimmen, dass er „möglichst gut” mit dem Informationswort $\underline{u}$ übereinstimmt.

$\text{Etwas genauer formuliert:}$  Es soll die Blockfehlerwahrscheinlichkeit ${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) $ bezogen auf die Vektoren $\underline{u}$ und $\underline{v}$ der Länge $k$ möglichst gering sein.

Aufgrund der eindeutigen Zuordnung $\underline{x} = {\rm enc}(\underline{u})$ durch den Kanalcoder bzw. empfängerseitig $\underline{v} = {\rm enc}^{-1}(\underline{z})$ gilt in gleicher Weise:

\[{\rm Pr(Blockfehler)} = {\rm Pr}(\underline{z} \ne \underline{x})\hspace{0.05cm}. \]

Der Kanaldecoder in obigem Modell besteht aus zwei Teilen:

• Der Codewortschätzer ermittelt aus dem Empfangsvektor $\underline{y}$ einen Schätzwert $\underline{z} \in \mathcal{C}$ gemäß einem vorgegebenen Kriterium.
  

• Aus dem (empfangenen) Codewort $\underline{z}$ wird das Informationswort $\underline{v}$  durch einfaches Mapping ermittelt, das mit $\underline{u}$ übereinstimmen sollte.
  
  

Für den Codewortschätzer gibt es insgesamt vier unterschiedliche Varianten, nämlich

• den Maximum–a–posteriori–Empfänger (MAP–Empfänger) für das gesamte Codewort $\underline{x}$,
  

• den Maximum–a–posteriori–Empfänger (MAP–Empfänger) für die einzelnen Codebits $x_i$,
  

• den Maximum–Likelihood–Empfänger (ML–Empfänger) für das gesamte Codewort $\underline{x}$,
  

• den Maximum–Likelihood–Empfänger (ML–Empfänger) für die einzelnen Codebits $x_i$.
  
  

Deren Definitionen folgen auf der nächsten Seite. Vorab aber gleich das Unterscheidungsmerkmal zwischen MAP und ML:

$\text{Fazit:}$ 

• Ein MAP–Empfänger berücksichtigt im Gegensatz zum ML–Empfänger auch unterschiedliche Auftrittswahrscheinlichkeiten für das gesamte Codewort bzw. für deren einzelne Bits.
  

• Sind alle Codeworte $\underline{x}$ und damit auch alle Codebits $x_i$ der Codeworte gleichwahrscheinlich, so ist der einfachere ML–Empfänger äquivalent zum entsprechenden MAP–Empfänger.

Definitionen der verschiedenen Optimalempfänger

$\text{Definition:}$  Der Maximum–a–posteriori–Empfänger auf Blockebene – kurz: block–wise MAP – entscheidet sich unter den $2^k$ Codeworten $\underline{x}_i \in \mathcal{C}$ für das Codewort mit der größten Rückschlusswahrscheinlichkeit (englisch: a–posteriori probability, APP):

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \vert\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]

${\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}\vert \hspace{0.05cm} \underline{y} )$ ist die bedingte Wahrscheinlichkeit, dass $\underline{x}_i$ gesendet wurde, wenn $\underline{y}$ empfangen wird.

Wir versuchen nun, diese Entscheidungsregel schrittweise zu vereinfachen. Die Rückschlusswahrscheinlichkeit kann nach dem „Satz von Bayes” wie folgt umgeformt werden:

\[{\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}\vert \hspace{0.05cm} \underline{y} ) = \frac{{\rm Pr}( \underline{y} \hspace{0.08cm} |\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) \cdot {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} )}{{\rm Pr}( \underline{y} )} \hspace{0.05cm}.\]

Die Wahrscheinlichkeit ${\rm Pr}( \underline{y}) $ ist unabhängig von $\underline{x}_i$ und muss bei der Maximierung nicht berücksichtigt werden. Sind zudem alle $2^k$ Informationsworte $\underline{u}_i$ gleichwahrscheinlich, so kann man bei der Maximierung auch auf den Beitrag ${\rm Pr}( \underline{x}_{\hspace{0.03cm}i} ) = 2^{-k}$ im Zähler verzichten.

$\text{Definition:}$  Der Maximum–Likelihood–Empfänger auf Blockebene – kurz: block–wise ML – entscheidet sich unter den $2^k$ zulässigen Codeworten $\underline{x}_i \in \mathcal{C}$ für das Codewort mit der größten Übergangswahrscheinlichkeit:

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm}\vert\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) \hspace{0.05cm}.\]

Die bedingte Wahrscheinlichkeit ${\rm Pr}( \underline{y} \hspace{0.05cm}\vert\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} )$ ist nun in Vorwärtsrichtung zu verstehen, nämlich als die Wahrscheinlichkeit, dass der Vektor $\underline{y}$ empfangen wird, wenn das Codewort $\underline{x}_i$ gesendet wurde.

Im Folgenden verwenden wir auf Blockebene stets den Maximum–Likelihood–Empfänger. Aufgrund der vorausgesetzten gleichwahrscheinlichen Informationsworte liefert auch dieser stets die bestmögliche Entscheidung.

Anders sieht es jedoch auf Bitebene aus. Ziel einer iterativen Decodierung ist es gerade, für alle Codebits $x_i \in \{0, 1\}$ Wahrscheinlichkeiten zu schätzen und diese an die nächste Stufe weiterzugeben. Hierzu benötigt man einen MAP–Empfänger.

$\text{Definition:}$  Der Maximum–a–posteriori–Empfänger auf Bitebene (kurz: bit–wise MAP) wählt für jedes einzelne Codebit $x_i$ den Wert ($0$ oder $1$) mit der größten Rückschlusswahrscheinlichkeit ${\rm Pr}( {x}_{\hspace{0.03cm}i}\vert \hspace{0.05cm} \underline{y} )$ aus:

\[\underline{z} = {\rm arg}\hspace{-0.1cm}{ \max_{ {x}_{\hspace{0.03cm}i} \hspace{0.03cm} \in \hspace{0.05cm} \{0, 1\} } \hspace{0.03cm} {\rm Pr}( {x}_{\hspace{0.03cm}i}\vert \hspace{0.05cm} \underline{y} ) \hspace{0.05cm} }.\]

Maximum-Likelihood–Entscheidung beim BSC–Kanal

Wenden wir nun das Maximum–Likelihood–Kriterium auf den gedächtnislosen BSC–Kanal an. Dann gilt:

\[{\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) = \prod\limits_{l=1}^{n} {\rm Pr}( y_l \hspace{0.05cm}|\hspace{0.05cm} x_l ) \hspace{0.2cm}{\rm mit}\hspace{0.2cm} {\rm Pr}( y_l \hspace{0.05cm}|\hspace{0.05cm} x_l ) = \left\{ \begin{array}{c} 1 - \varepsilon\\ \varepsilon \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls} \hspace{0.15cm} y_l = x_l \hspace{0.05cm},\\ {\rm falls} \hspace{0.15cm}y_l \ne x_l\hspace{0.05cm}.\\ \end{array} \hspace{0.05cm}.\]

\[\Rightarrow \hspace{0.3cm} {\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) = \varepsilon^{d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \cdot (1-\varepsilon)^{n-d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \hspace{0.05cm}.\]

$\text{Beweis:}$  Dieses Ergebnis lässt sich wie folgt begründen:

• Die Hamming–Distanz $d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ gibt die Anzahl der Bitpositionen an, in denen sich die Worte $\underline{y}$ und $\underline{x}_{\hspace{0.03cm}i}$ mit jeweils $n$ binären Elementen unterscheiden. Beispiel: Die Hamming–Distanz zwischen $\underline{y}= (0, 1, 0, 1, 0, 1, 1)$ und $\underline{x}_{\hspace{0.03cm}i} = (0, 1, 0, 0, 1, 1, 1)$ ist $2$.
  

• In $n - d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ Positionen unterscheiden sich demnach die beiden Vektoren $\underline{y}$ und $\underline{x}_{\hspace{0.03cm}i}$ nicht. Im obigen Beispiel sind fünf der $n = 7$ Bit identisch.
• Zu obiger Gleichung kommt man schließlich durch Einsetzen der Verfälschungswahrscheinlichkeit $\varepsilon$ bzw. deren Ergänzung $1-\varepsilon$.

Die Vorgehensweise bei der Maximum–Likelihood–Detektion ist, dasjenige Codewort $\underline{x}_{\hspace{0.03cm}i}$ zu finden, das die Übergangswahrscheinlichkeit ${\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} )$ maximiert:

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} \left [ \varepsilon^{d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \cdot (1-\varepsilon)^{n-d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \right ] \hspace{0.05cm}.\]

Da der Logarithmus eine monoton steigende Funktion ist, erhält man das gleiche Ergebnis nach folgender Maximierung:

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} L(\underline{x}_{\hspace{0.03cm}i})\hspace{0.5cm} {\rm mit}\hspace{0.5cm} L(\underline{x}_{\hspace{0.03cm}i}) = \ln \left [ \varepsilon^{d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \cdot (1-\varepsilon)^{n-d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \right ] \]

\[ \Rightarrow \hspace{0.3cm} L(\underline{x}_{\hspace{0.03cm}i}) = d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}) \cdot \ln \hspace{0.05cm} \varepsilon + \big [n -d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\big ] \cdot \ln \hspace{0.05cm} (1- \varepsilon) = \ln \frac{\varepsilon}{1-\varepsilon} \cdot d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}) + n \cdot \ln \hspace{0.05cm} (1- \varepsilon) \hspace{0.05cm}.\]

Hierbei ist zu berücksichtigen:

• Der zweite Term dieser Gleichung ist unabhängig von $\underline{x}_{\hspace{0.03cm}i}$ und muss für die Maximierung nicht weiter betrachtet werden.
• Auch der Faktor vor der Hamming–Distanz ist für alle $\underline{x}_{\hspace{0.03cm}i}$ gleich.
• Da $\ln \, {\varepsilon}/(1-\varepsilon)$ negativ ist (zumindest für $\varepsilon <0.5$, was ohne große Einschränkung vorausgestzt werden kann), wird aus der Maximierung eine Minimierung, und man erhält folgendes Endergebnis:
  

$\text{Maximum–Likelihood-Entscheidung beim BSC-Kanal:}$ 

Wähle von den $2^k$ zulässigen Codeworten $\underline{x}_{\hspace{0.03cm}i}$ dasjenige mit der geringsten Hamming–Distanz  $d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ zum Empfangsvektor $\underline{y}$  aus:

\[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}, \hspace{0.2cm} \underline{y} \in {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]

Anwendungen der ML/BSC–Entscheidung finden Sie auf den folgenden Seiten:

• Single Parity–check Code (SPC)
  

• Wiederholungscode (englisch: Repetition Code, RC).
  

Maximum-Likelihood–Entscheidung beim AWGN–Kanal

Das AWGN–Modell für einen $(n, k)$–Blockcode unterscheidet sich vom Modell auf der ersten Kapitelseite dadurch, dass für $x$,  $\tilde{x}$  und  $y$  nun die entsprechenden Vektoren $\underline{x}$,  $\underline{\tilde{x}}$  und  $\underline{y}$  verwendet werden müssen, jeweils bestehend aus $n$ Elementen.

Die Schritte zur Herleitung des Maximum–Likelihood–Entscheiders bei AWGN werden nachfolgend nur stichpunktartig angegeben:

• Der AWGN–Kanal ist per se gedächtnislos (hierfür steht das „White” im Namen). Für die bedingte Wahrscheinlichkeitsdichtefunktion kann somit geschrieben werden kann:

\[f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}} ) = \prod\limits_{l=1}^{n} f( y_l \hspace{0.05cm}|\hspace{0.05cm} \tilde{x}_l ) \hspace{0.05cm}.\]

• Die bedingte WDF ist für jedes einzelne Codeelement $(l = 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, n)$ gaußisch. Damit genügt auch die gesamte WDF einer (eindimensionalen) Gaußverteilung:

\[f({y_l \hspace{0.03cm}| \hspace{0.03cm}\tilde{x}_l }) = \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot \exp \left [ - \frac {(y_l - \tilde{x}_l)^2}{2\sigma^2} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}} ) = \frac {1}{(2\pi)^{n/2} \cdot \sigma^n } \cdot \exp \left [ - \frac {1}{2\sigma^2} \cdot \sum_{l=1}^{n} \hspace{0.2cm}(y_l - \tilde{x}_l)^2 \right ] \hspace{0.05cm}.\]

• Da $\underline{y}$  nun nicht mehr wie beim BSC–Modell wertdiskret ist, sondern wertkontinuierlich, müssen jetzt nach der ML–Entscheidungsregel Wahrscheinlichkeitsdichten untersucht werden und nicht mehr Wahrscheinlichkeiten. Das optimale Ergebnis lautet:

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}}_i )\hspace{0.05cm}, \hspace{0.5cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]

• In der Algebra bezeichnet man den Abstand zweier Punkte $\underline{y}$  und $\underline{\tilde{x}}$  im $n$–dimensionalen Raum als die Euklidische Distanz, benannt nach dem griechischen Mathematiker Euklid, der im dritten Jahrhundert vor Christus lebte:

\[d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{\tilde{x}}) = \sqrt{\sum_{l=1}^{n} \hspace{0.2cm}(y_l - \tilde{x}_l)^2}\hspace{0.05cm},\hspace{0.8cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in \mathcal{C} \hspace{0.05cm}.\]

• Damit lautet die ML–Entscheidungsregel beim AWGN–Kanal für einen jeden Blockcode unter Berücksichtigung der Tatsache, dass der erste Faktor der WDF $f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}_i} )$ konstant ist:

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} \exp \left [ - \frac {d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{\tilde{x}}_i)}{2\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.8cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]

Nach einigen weiteren Zwischenschritten kommt man zum Ergebnis:

$\text{Maximum–Likelihood-Entscheidung beim AWGN-Kanal:}$ 

Wähle von den $2^k$ zulässigen Codeworten $\underline{x}_{\hspace{0.03cm}i}$ dasjenige mit der kleinsten Euklidischen Distanz  $d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$  zum Empfangsvektor  $\underline{y}$  aus:

\[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}, \hspace{0.8cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]

Aufgaben zum Kapitel

Aufgabe 1.3: Kanalmodelle BSC–BEC–BSEC–AWGN

Aufgabe 1.4: Maximum–Likelihood–Entscheidung