Applets:Zur Verdeutlichung der Pseudoternärcodes: Unterschied zwischen den Versionen
| Zeile 114: | Zeile 114: | ||
* Ist $s(t)$ die Musterfunktion eines stationären und ergodischen Zufallsprozesses, so gilt für die [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Zufallsprozesse_.281.29|Autokorrelationsfunktion]] $\rm (AKF)$: | * Ist $s(t)$ die Musterfunktion eines stationären und ergodischen Zufallsprozesses, so gilt für die [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Zufallsprozesse_.281.29|Autokorrelationsfunktion]] $\rm (AKF)$: | ||
:$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} | :$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - | \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - | ||
\lambda \cdot T)\hspace{0.05cm}.$$ | \lambda \cdot T)\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Diese Gleichung beschreibt die Faltung der diskreten AKF $\varphi_a(\lambda) = {\rm E}\big [ a_\nu \cdot a_{\nu + \lambda}\big]$ der Amplitudenkoeffizienten mit der Energie–AKF des Grundimpulses: | |
| − | |||
| − | \varphi_a(\lambda | ||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| + | :$$\varphi^{^{\bullet} }_{g}(\tau) = | ||
| + | \int_{-\infty}^{+\infty} g ( t ) \cdot g ( t + | ||
| + | \tau)\,{\rm d} t \hspace{0.05cm}.$$ | ||
| − | + | *Der Punkt soll darauf hinweisen, dass $\varphi^{^{\bullet} }_{g}(\tau)$ die Einheit einer Energie besitzt, während $\varphi_s(\tau)$ eine Leistung angibt und $\varphi_a(\lambda)$ dimensionslos ist. | |
| − | Die Entsprechungsgröße zur | + | *Die Entsprechungsgröße zur AKF $\varphi_s(\tau)$ ist im Frequenzbereich das [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)#Theorem_von_Wiener-Chintchine|Leistungsdichtespektrum]] $\rm (LDS)$ ${\it \Phi}_s(f)$, das mit der AKF über das Fourierintegral in einem festen Bezug steht:<br> |
:$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | :$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | ||
{\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot | {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot | ||
Version vom 30. Juli 2020, 13:35 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Das Applet soll die Eigenschaften des so genannten „Matched-Filters” $({\rm MF})$ verdeutlichen. Dieses dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude und/oder der Lage einer bekannten Signalform in einer stark verrauschten Umgebung. Oder allgemeiner gesprochen: Das Matched-Filter – manchmal auch als „Optimalfilter” oder als „Korrelationsfilter” bezeichnet – dient dem Nachweis der Signalexistenz.
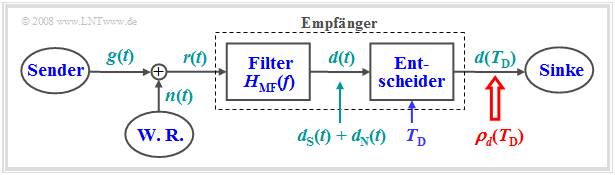
Die Grafik zeigt den so genannten Matched-Filter-Empfänger:
- Dieser kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem Signal–zu–Rausch–Verhältnis $($englisch: signal–to–noise–ratio, $\rm SNR)$ – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht.
- Eine Anwendung ist die Radartechnik, bei der man zwar die Impulsform $g(t)$ kennt, nicht aber, wann der Impuls gesendet wurde und mit welcher Stärke und Verzögerung dieser ankommt.
- Das Matched-Filter wird aber auch als Empfangsfilter in digitalen Übertragungssystemen (oder zumindest als Teil davon) eingesetzt, um die Fehlerwahrscheinlichkeit des Systems zu minimieren.
Alle Parameter, Zeiten und Frequenzen sind als normierte Größen zu verstehen und damit dimensionslos.
- Für den Eingangsimpuls $g(t)$ sind „Rechteck”, „Gauß” und „Exponential” einstellbar, die jeweils durch die Impulsamplitude $A_g$, die äquivalente Impulsdauer $\Delta t_g$ sowie die Verschiebung $\tau_g$ gegenüber dem (hinsichtlich Zeit) symmetrischen Fall beschrieben werden. Weitere Informationen im Abschnitt Weitere Angaben zu den betrachteten Eingangsimpulsen.
- Für das Empfangsfilter kann zwischen den Alternativen „Spalt–Tiefpass”, „Gauß–Tiefpass”, „Tiefpass erster Ordnung”und „extrem akausales Filter” gewählt werden. Dargestellt werden die jeweiligen Impulsantworten $h(t)$, gekennzeichnet durch deren Höhe $A_h$, die äquivalente Dauer $\Delta t_h$ und die Verschiebung $\tau_h$. Weitere Informationen im Abschnitt Weitere Angaben zu den betrachteten Impulsantworten.
- Weitere Eingabeparameter sind der Detektionszeitpunkt $T_{\rm D}$ sowie die ebenfalls normierte Rauschleistungsdichte $N_0$ am Empfängereingang.
Als Numerikwerte ausgegeben werden
- die Energie $E_g$ des Eingangsimpulses $g(t)$, der Nutzabtastwert $d_{\rm S} (T_{\rm D})$ am Filterausgang sowie die Rauschvarianz $\sigma_d^2$ am Filterausgang,
- das Signal–zu–Rausch–Verhältnis $\rm (SNR)$ $\rho_{d} (T_{\rm D})$ am Filterausgang und die zugehörige dB–Angabe $10 \cdot \lg \ \rho_{d} (T_{\rm D})$,
- der hierfür maximale Wert $10 \cdot \lg \ \rho_{\rm MF}$.
Erfüllt die eingegebene Konfiguration die Matched-Filter-Bedingungen, dann gilt: $10 \cdot \lg \ \rho_{d} (T_{\rm D,\ opt}) = 10 \cdot \lg \ \rho_{\rm MF}$.
Theoretischer Hintergrund
Allgemeine Beschreibung der Pseudoternärcodes
Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die Ordnung des Codes.
Typisch für eine symbolweise Codierung ist, dass
- die Symboldauer $T$ des Codersignals (und des Sendesignals) mit der Bitdauer $T_{\rm B}$ des binären Quellensignals übereinstimmt, und
- Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.
Besondere Bedeutung besitzen Pseudomehrstufencodes – besser bekannt unter der englischen Bezeichnung Partial Response Codes.
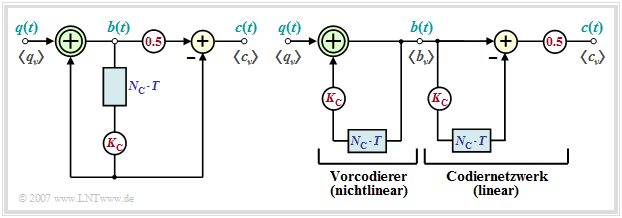
- Im Folgenden werden ausschließlich Pseudoternärcodes ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind.
- In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist.
Man erkennt aus den beiden Darstellungen:
- Der Pseudoternärcodierer kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man – wie im rechten Ersatzschaltbild dargestellt – die Verzögerung um $N_{\rm C} \cdot T$ und die Gewichtung mit $K_{\rm C}$ zur Verdeutlichung zweimal zeichnet.
- Der nichtlineare Vorcodierer gewinnt durch eine Modulo–2–Addition („Antivalenz”) zwischen den Symbolen $q_\nu$ und $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $ die vorcodierten Symbole $b_\nu$, die ebenfalls binär sind:
- $$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, +1\}\hspace{0.05cm}.$$
- Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.
- Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das lineare Codiernetzwerk durch die herkömmliche Subtraktion
- $$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$
- das durch folgende Impulsantwort bzw. Übertragungsfunktion bezüglich dem Eingangssignal $b(t)$ und dem Ausgangssignal $c(t)$ beschrieben werden kann:
- $$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$
- Die relative Coderedundanz ist für alle Pseudoternärcodes gleich. Setzt man in die allgemeine Definitionsgleichung $M_q=2$, $M_c=3$ und $T_c =T_q$ ein, so erhält man
- $$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$
Das $\text{Sendesignal aller Pseudoternärcodes}$ wird im Folgenden stets wie folgt dargestellt:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$
- Die Eigenschaft des aktuellen Pseudoternärcodes spiegelt sich in den statistischen Bindungen zwischen den $a_\nu$ wider. In allen Fällen gilt $a_\nu \in \{-1, \ 0, +1\}$.
- Der Sendegrundimpuls $g(t)$ stellt zum einen die erforderliche Energie bereit, hat aber auch Einfluss auf die statistischen Bindungen innerhalb des Signals.
- Im Programm ausgewählt werden kann neben dem NRZ–Rechteckimpuls $g_{\rm R}(t)$:
- der Nyquistimpuls ⇒ Impulsantwort des Cosinus–Rolloff–Tiefpasses mit Rolloff–Faktor $r$: $g_{\rm Nyq}(t)={\rm const.} \cdot \frac{\cos(\pi \cdot r\cdot t/T)}{1-(2\cdot r\cdot t/T)^2} \cdot {\rm si}(\pi \cdot t/T),$
- der Wurzel–Nyquistimpuls ⇒ ????? des Cosinus–Rolloff–Tiefpasses mit Rolloff–Faktor $r$: $g_{\sqrt{\rm Nyq} }(t)={\rm const.} \cdot \frac{\cos(\pi \cdot r\cdot t/T)}{1-(2\cdot r\cdot t/T)^2} \cdot {\rm si}(\pi \cdot t/T),$
Eigenschaften des AMI-Codes
Die Pseudoternärcodes unterscheiden sich in den Parametern $N_{\rm C}$ und $K_{\rm C}$. Der bekannteste Vertreter ist der Bipolarcode erster Ordnung mit den Codeparametern $N_{\rm C} = 1$ und $K_{\rm C} = 1$, der auch unter der Bezeichnung AMI–Code (von: Alternate Mark Inversion) bekannt ist.
Dieser wird zum Beispiel bei ISDN (Integrated Services Digital Networks) auf der so genannten $S_0$–Schnittstelle eingesetzt.
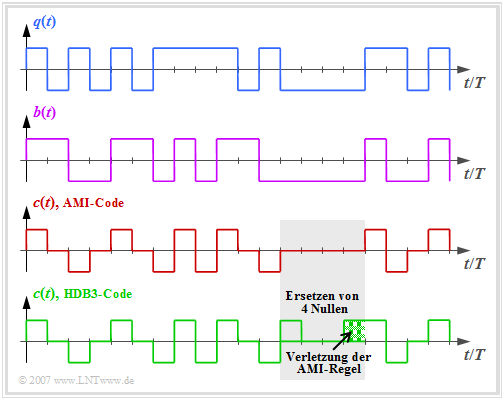
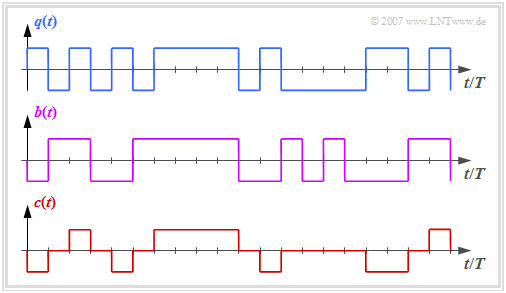
Die Grafik zeigt oben das binäre Quellensignal $q(t)$. Im zweiten und dritten Diagramm sind dargestellt:
- das ebenfalls binäre Signal $b(t)$ nach dem Vorcodierer, und
- das Codersignal $c(t) = s(t)$ des AMI–Codes.
Man erkennt das einfache AMI–Codierprinzip:
- Jeder Binärwert „-1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Koeffizienten $a_\nu = 0$ codiert.
- Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt.
Damit wird sichergestellt, dass im AMI–codierten Signal keine langen „+1”– und auch keine keine langen „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal zu Problemen führen würde.
Dagegen ist das Auftreten langer Nullfolgen durchaus möglich, bei denen über einen längeren Zeitraum keine Taktinformation übertragen wird.
Um dieses zweite Problem zu vermeiden, wurden einige modifizierte AMI–Codes entwickelt, zum Beispiel der B6ZS–Code und der HDB3–Code:
- Beim HDB3–Code (grüne Kurve in obiger Grafik) werden vier aufeinanderfolgende Nullen im AMI–codierten Signal durch eine Teilsequenz ersetzt, die die AMI–Codierregel verletzt.
- Im grau hinterlegten Bereich ist dies die Folge „+ 0 0 +”, da das letzte Symbol vor der Ersetzung ein „Minus” war.
- Damit ist beim HDB3–Code die Anzahl aufeinanderfolgender Nullen auf $3$ begrenzt und beim B6ZS–Code auf $5$.
- Der Decoder erkennt diese Codeverletzung und ersetzt „+ 0 0 +” wieder durch „0 0 0 0”.
Zur AKF– und LDS-Berechnung eines Digitalsignals
In der Versuchsdurchführung werden einige Größen und Zusamenhänge verwendet, die hier kurz eräutert werden sollen:
- Das (zeitlich unbegrenzte) Digitalsignal beinhaltet sowohl die Quellenstatistik $($Amplitudenkoeffizienten $a_\nu$) als auch die Sendeimpulsform $g(t)$:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g ( t - \nu \cdot T)\hspace{0.05cm}.$$
- Ist $s(t)$ die Musterfunktion eines stationären und ergodischen Zufallsprozesses, so gilt für die Autokorrelationsfunktion $\rm (AKF)$:
- $$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
- Diese Gleichung beschreibt die Faltung der diskreten AKF $\varphi_a(\lambda) = {\rm E}\big [ a_\nu \cdot a_{\nu + \lambda}\big]$ der Amplitudenkoeffizienten mit der Energie–AKF des Grundimpulses:
- $$\varphi^{^{\bullet} }_{g}(\tau) = \int_{-\infty}^{+\infty} g ( t ) \cdot g ( t + \tau)\,{\rm d} t \hspace{0.05cm}.$$
- Der Punkt soll darauf hinweisen, dass $\varphi^{^{\bullet} }_{g}(\tau)$ die Einheit einer Energie besitzt, während $\varphi_s(\tau)$ eine Leistung angibt und $\varphi_a(\lambda)$ dimensionslos ist.
- Die Entsprechungsgröße zur AKF $\varphi_s(\tau)$ ist im Frequenzbereich das Leistungsdichtespektrum $\rm (LDS)$ ${\it \Phi}_s(f)$, das mit der AKF über das Fourierintegral in einem festen Bezug steht:
- $$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} \,{\rm d} \tau \hspace{0.05cm}.$$
Berücksichtigt man den Zusammenhang zwischen Energie–AKF und Energiespektrum,
- $$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm},$$
sowie den Verschiebungssatz, so kann das Leistungsdichtespektrum des Digitalsignals $s(t)$ in folgender Weise dargestellt werden:
- $${\it \Phi}_s(f) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it \Phi}^{^{\hspace{0.05cm}\bullet}}_{gs}(f) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = {1}/{T} \cdot |G_s(f)|^2 \cdot \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( 2 \pi f \lambda T)\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass ${\it \Phi}_s(f)$ und $|G_s(f)|^2$ reellwertig sind und gleichzeitig $\varphi_a(-\lambda) =\varphi_a(+\lambda)$ gilt.
Definiert man nun die spektrale Leistungsdichte der Amplitudenkoeffizienten zu
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} = \varphi_a(0) + 2 \cdot \sum_{\lambda = 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f \lambda T) \hspace{0.05cm},$$
so erhält man den folgenden Ausdruck:
- $${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot |G_s(f)|^2 \hspace{0.05cm}.$$
$\text{Fazit:}$ Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ eines Digitalsignals $s(t)$ kann als Produkt zweier Funktionen dargestellt werden::
- Der erste Term ${\it \Phi}_a(f)$ ist dimensionslos und beschreibt die spektrale Formung des Sendesignals durch die statistischen Bindungen der Quelle.
- Dagegen berücksichtigt $\vert G_s(f) \vert^2$ die spektrale Formung durch den Sendegrundimpuls $g_s(t)$. Je schmaler dieser ist, desto breiter ist $\vert G_s(f) \vert^2$ und um so größer ist damit der Bandbreitenbedarf.
- Das Energiespektrum hat die Einheit $\rm V^2s/Hz$ und das Leistungsdichtespektrum – aufgrund der Division durch den Symbolabstand $T$ – die Einheit $\rm V^2/Hz$. Beide Angaben gelten wieder nur für den Widerstand $1 \ \rm \Omega$.
Leistungsdichtespektrum des AMI-Codes
Der Frequenzgang des linearen Codiernetzwerks eines Pseudoternärcodes lautet allgemein:
- $$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi\hspace{0.03cm}\cdot \hspace{0.03cm}f \hspace{0.03cm}\cdot \hspace{0.03cm} N_{\rm C}\hspace{0.03cm}\cdot \hspace{0.03cm}T} \big] ={1}/{2} \cdot \big [1 - K \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} \alpha} \big ]\hspace{0.05cm}.$$
Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten $(K$ und $\alpha$ sind Abkürzungen entsprechend obiger Gleichung$)$:
- $$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos (\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos (\alpha) \big ] $$
- $$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ] \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$
Insbesondere erhält man für das Leistungsdichtespektrum (LDS) des AMI–Codes $(N_{\rm C} = K_{\rm C} = 1)$:
- $${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$$
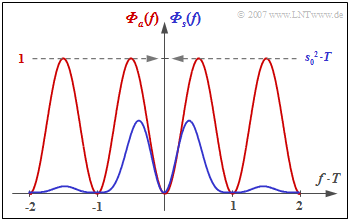
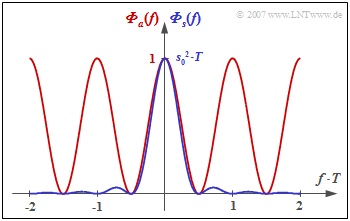
Die Grafik zeigt
- das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten (rote Kurve), und
- das LDS ${\it \Phi}_s(f)$ des gesamten Sendesignals (blau), gültig für NRZ–Rechteckimpulse.
Man erkennt aus dieser Darstellung
- die Gleichsignalfreiheit des AMI–Codes, da ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$ ist,
- die Leistung $P_{\rm S} = s_0^2/2$ des AMI–codierten Sendesignals (Integral über ${\it \Phi}_s(f)$ von $- \infty$ bis $+\infty$).
Hinweise:
- Das LDS von HDB3– und B6ZS–Code weicht von dem des AMI–Codes nur unwesentlich ab.
- Die hier behandelte Thematik können Sie sich mit dem interaktiven Applet Signale, AKF und LDS der Pseudoternärcodes verdeutlichen.
Eigenschaften des Duobinärcodes
Der Duobinärcode ist durch die Codeparameter $N_{\rm C} = 1$ und $K_{\rm C} = -1$ festgelegt. Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten bzw. für das LDS des Sendesignals:
- $${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm},$$
- $$ {\it \Phi}_s(f) = s_0^2 \cdot T \cdot \cos^2 (\pi f T)\cdot {\rm si}^2 (\pi f T)= s_0^2 \cdot T \cdot {\rm si}^2 (2 \pi f T) \hspace{0.05cm}.$$
Die Grafik zeigt das Leistungsdichtespektrum
- der Amplitudenkoeffizienten ⇒ ${\it \Phi}_a(f)$ als rote Kurve,
- des gesamten Sendsignals ⇒ ${\it \Phi}_s(f)$ als blaue Kurve.
In der zweiten Grafik sind die Signale $q(t)$, $b(t)$ und $c(t) = s(t)$ skizziert. Wir verweisen hier wieder auf das Applet Signale, AKF und LDS der Pseudoternärcodes, das auch die Eigenschaften des Duobinärcodes verdeutlicht.
Aus diesen Darstellungen geht hervor:
- Beim Duobinärcode können beliebig viele Symbole mit gleicher Polarität („+1” bzw. „–1”) direkt aufeinanderfolgen.
- Deshalb gilt ${\it \Phi}_a(f = 0)=1$ und ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.
- Dagegen tritt beim Duobinärcode die alternierende Folge „ ... , +1, –1, +1, –1, +1, ... ” nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist.
- Deshalb gilt beim Duobinärcode: ${\it \Phi}_s(f = 1/(2T) = 0$.
- Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ des pseudoternären Duobinärcodes ist identisch mit dem LDS bei redundanzfreier Binärcodierung mit halber Rate $($Symboldauer $2T)$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ... , 11) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
- Alle Zeiten, Frequenzen, Signalwerte und Leistungen sind normiert zu verstehen.
(1) Betrachten und interpretieren Sie die binäre Vorcodierung des AMI–Codes anhand der Quellensymbolfolge $\rm C$ unter der Annahme $b_0 = +1$.
- Die Modulo–2–Addition kann auch als Antivalenz aufgefasst werden. Es gilt $b_{\nu} = +1$, falls sich $q_{\nu}$ und $b_{\nu – 1}$ unterscheiden, andernfalls ist $b_{\nu} = -1$ zu setzen:
- $b_1 = (x_1 = +1)\ {\rm XOR}\ (b_0= +1) = -1,\ \ b_2 = (x_2 = -1)\ {\rm XOR}\ (b_1= -1) = -1,\ \ b_3 = (x_3 = -1)\ {\rm XOR}\ (b_2= -1) = -1,$
- $b_4 = (x_4 = +1)\ {\rm XOR}\ (b_3= -1) = +1,\ \ b_5 = (x_5 = +1)\ {\rm XOR}\ (b_4= +1) = -1,\ \ b_6 = (x_6 = +1)\ {\rm XOR}\ (b_5= -1) = +1,\ \ b_7 = b_8 = \text{...} = -1.$
- Mit der Startbedingung $b_0 = -1$ ergibt sich die negierte Folge: $b_4 = b_6 =-1$. Alle anderen $b_\nu = +1$.
(2) Es gelte $b_0 = +1$. Betrachten Sie die AMI–Coderfolge $\langle c_\nu \rangle$ der Quellensymbolfolge $\rm C$ und geben Sie deren Ampltitudenkoeffizienten $a_\nu$ an.
- Es gilt: $a_1= 0.5 \cdot (b_1-b_0) = -1$, $a_2= 0.5 \cdot (b_2-b_1) =0$, $a_3= 0.5 \cdot (b_3-b_2) =0$, $a_4= +1$, $a_5= -1$, $a_6= +1$, $a_7= -1$, $a_8= a_9 =-1= \text{...} = 0$.
- Im Gegensatz zur Vorcodierung ist hier die herkömmliche Addition (Subtraktion) anzuwenden und nicht die Modulo–2– Addition.
(3) Betrachten Sie nun die AMI–Codierung für mehrere Zufallsfolgen. Welche Regeln lassen sich aus diesen Versuchen für die Ampltitudenkoeffizienten $a_\nu$ ableiten?
- Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Koeffizienten $a_\nu = 0$ codiert. Es können beliebig viele $a_\nu = 0$ aufeinanderfolgen.
- Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt, beginnend mit $a_\nu = -1$, falls $b_0 = +1$.
- Aus der Quellensymbolfolge $\rm A$ ⇒ $\langle \hspace{0.05cm}q_\nu \equiv +1 \hspace{0.05cm}\rangle$ wird die Codesymbolfolge $+1, -1, +1, -1, \text{...}$ . Lange Folgen $\langle \hspace{0.05cm}c_\nu \equiv +1 \hspace{0.05cm}\rangle$ bzw. $\langle \hspace{0.05cm}c_\nu \equiv -1 \hspace{0.05cm}\rangle$ sind ausgeschossen.
Dummy
(4) Weiterhin AMI–Codierung. Interpretieren Sie die Autokorrelationsfunktion $\varphi_a(\lambda)$ der Amplitudenkoeffizienten und das Leistungsdichtespektrum $\Phi_a(f)$.
- Die diskrete AKF $\varphi_a(\lambda)$ der Amplitudenkoeffizienten ist nur für ganzzahlige $\lambda$–Werte definiert. Beim AMI–Code $(N_{\rm C}=1)$ sind für $|\lambda| > 1$ alle $\varphi_a(\lambda)= 0$.
- $\varphi_a(\lambda = 0)$ ist gleich dem quadratischen Mittelwert der Amplitudenkoeffizienten ⇒ $\varphi_a(\lambda = 0) = {\rm Pr}(a_\nu = +1) \cdot (+1)^2 + {\rm Pr}(a_\nu = -1) \cdot (-1)^2 = 0.5.$
- Zum Erwartungswert ${\rm E}\big [a_\nu \cdot a_{\nu+1}\big]$ tragen nur die Kombinationen $(+1, -1)$ und $(-1, +1)$ bei. Ergebnis: $\varphi_a(\lambda = \pm 1)={\rm E}\big [a_\nu \cdot a_{\nu+1}\big]=-0.25.$
- Das Leistungsdichtespektrum $\Phi_a(f)$ ist die Fouriertransformierte der diskreten AKF $\varphi_a(\lambda)$. Das Ergebnis ist ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$
- Aus der Gleichsignalfreiheit ⇒ ${\it \Phi}_a(f = 0) = 0$ folgt: Der AMI–Code ist insbesondere für Kanäle interessant, über die kein Gleichanteil übertragen werden kann.
(5) Wir betrachten weiter die AMI–Codierung und den Rechteckimpuls. Interpretieren Sie die AKF $\varphi_s(\tau)$ des Sendesignals und das LDS $\Phi_s(f)$.
- Die AKF $\varphi_s(\tau)$ des Sendesignals ergibt sich aus der Faltung der diskreten AKF $\varphi_a(\lambda)$ mit der Energie–AKF $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$ des Sendegrundimpulses $g(t)$.
- Bei rechteckförmigem Impuls ist $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$ dreieckförmig. nur für ganzzahlige $\lambda$–Werte definiert. Beim AMI–Code $(N_{\rm C}=1)$ sind für $|\lambda| > 1$ alle $\varphi_a(\lambda)= 0$.
- $\varphi_a(\lambda = 0)$ ist gleich dem quadratischen Mittelwert der Amplitudenkoeffizienten ⇒ $\varphi_a(\lambda = 0) = {\rm Pr}(a_\nu = +1) \cdot (+1)^2 + {\rm Pr}(a_\nu = -1) \cdot (-1)^2 = 0.5.$
- Zum Erwartungswert ${\rm E}\big [a_\nu \cdot a_{\nu+1}\big]$ tragen nur die Kombinationen $(+1, -1)$ und $(-1, +1)$ bei. Ergebnis: $\varphi_a(\lambda = \pm 1)={\rm E}\big [a_\nu \cdot a_{\nu+1}\big]=-0.25.$
- Das Leistungsdichtespektrum $\Phi_a(f)$ ist die Fouriertransformierte der diskreten AKF $\varphi_a(\lambda)$. Das Ergebnis ist ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$
- $$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm},$$
(5) Es gelten wieder die Einstellungen von (3) mit Ausnahme einer niedrigeren Impulsantwort $A_h = 0.8 $ statt $A_h = 1$. Interpretieren Sie die Veränderungen.
- Es handelt sich auch mit $A_h \ne A_g$ um ein Matched-Filter, solange $h(t)$ formgleich mit $g(t)$ ist ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
- Die Gleichung $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ führt zum gleichen Ergebnis, da ${d_{\rm S}}^2 (T_{\rm D})$ und $\sigma_d^2$ gegenüber (3) jeweils um den Faktor $0.8^2$ vermindert wird.
(6) Gegenüber (5) wird nun die Höhe des Eingangsimpulses $g(t)$ von $A_g = 1$ auf $A_g = 1.25$ erhöht. Beschreibt hier $h(t)$ ein Matched-Filter? Wie groß ist $\rho_{\rm MF}$?
- Auch hier liegt ein Matched-Filter vor, da $h(t)$ und $g(t)$ formgleich sind. Mit $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} \approx 21.9$ dB.
- Der höhere Wert $21.9$ dB gegenüber (5) lässt sich dadurch erklären, dass bei gleicher Rauschvarianz $\sigma_d^2= 0.0064$ der Nutzabtastwert wieder ${d_{\rm S}} (T_{\rm D}) = 1$ ist.
(7) Wir gehen weiter von der Rechteck–Rechteck–Kombination aus mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=0$.
Interpretieren Sie die Ergebnisse nach Variation der äquivalenten Impulsdauer $\Delta t_h$ von $h(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_h$.
- Das Optimum ergibt sich erwartungsgemäß für die äquivalente Impulsdauer $\Delta t_h=\Delta t_g=1$. Dann ist $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =20$ dB $\big(= 10 \cdot \lg \rho_{\rm MF}\big)$.
- Ist $\Delta t_h<\Delta t_g=1$, so ist das Nutzsignal trapezförmig. Für $\Delta t_h=0.6$: $d_{\rm S} (T_{\rm D}=0)= 0.6$ und $\sigma_d^2\approx0.006$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 17.8$ dB.
- Auch für $\Delta t_h>1$ ist das Nutzsignal trapezförmig, aber trotzdem $d_{\rm S} (T_{\rm D}=0)= 1$. Die Rauschvarianz $\sigma_d^2$ nimmt kontinuierlich mit $\Delta t_h$ zu.
- Für $\Delta t_h=1.4$ ist $\sigma_d^2=0.0140$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 18.5$ dB. Gegenüber dem Matched–Filter $(\Delta t_h=1)$ beträgt die Verschlechterung ca. $1.5$ dB.
(8) Interpretieren Sie nun die Ergebnisse für verschiedene $\Delta t_g$ des Eingangsimpulses $g(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_g$.
- Beachten Sie: Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ ist die Differenz aus $20\cdot \lg \ \big [{K \cdot d_{\rm S}} (T_{\rm D,\ opt}) \big ]$ (violette Kurve) und $20\cdot \lg \ \big [K \cdot \sigma_d \big ]$ (grüne Kurve).
- Beim betrachteten Parametersatz und $K=10$ ist der grüne Term $20\cdot \lg \ \big [K \cdot \sigma_d \big ] = 0$ dB für alle $\Delta t_g$ ⇒ die blaue und die violette Kurve sind identisch.
- Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ steigt von $15.6$ dB $($für $\Delta t_g = 0.6)$ bis $20$ dB $($für $\Delta t_g = 1)$ kontinuierlich an und bleibt für $\Delta t_g > 1$ dann konstant.
- Die Einstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ ergibt aber kein Matched-Filter. Vielmehr gilt mit $\Delta t_h = \Delta t_g = 1.4$: $10 \cdot \lg \ \rho_{\rm MF}=10 \cdot \lg \ (2 \cdot E_g/N_0) \approx 21.5$ dB.
- Die Grafikdarstellung über $\Delta t_h$ mit der Grundeinstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ zeigt nun einen monotonen Anstieg der blauen Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$.
- Für $\Delta t_h = 0.6$ ergibt sich $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 17.8$ dB, für $\Delta t_h = 1.4$ dagegen $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 21.5$ dB $=10 \cdot \lg \ \rho_{\rm MF}$.
(9) Wir betrachten den Exponentialimpuls $g(t)$ und den Tiefpass erster Ordnung sowie $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=1$.
Erfüllt diese Einstellung den Matched-Filter-Kriterien? Begründen Sie Ihre Antworten mit möglichst vielen Argumenten.
- Hier gilt $h(t)=g(t)$. Bei einer Matched-Filter-Konfiguration müsste $h(t)={\rm const.} \cdot g(T_{\rm D}-t)$ gelten.
- Das Detektionsnutzsignal $d_{\rm S}(t)$ hat keinen symmetrischen Verlauf um das Maximum. Beim Matched-Filter müsste $d_{\rm S}(T_{\rm D}-t) = d_{\rm S}(T_{\rm D}+t) $ gelten.
- Trotz $\Delta t_h=\Delta t_g$ ist $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) \approx 14.3$ dB kleiner als $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 \approx 17$ dB.
(10) Was ändert sich bei sonst gleichen Einstellungen mit dem „extrem akausalen Filter”? Erfüllt die Einstellung die Matched-Filter-Kriterien? Begründung.
- Hier gilt nun $h(t)=g(-t)$ und das Detektionsnutzsignal $d_{\rm S}(t)$ ist symmetrisch um $t=0$. Sinnvollerweise sollte hier $T_{\rm D} = 0 $ gewählt werden.
- Damit erhält man für $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) =10 \cdot \lg \ d_{\rm S}^2 (T_{\rm D,\ opt})/\sigma_d^2 = 17$ dB den gleichen Wert wie für $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 = 17$ dB.
- Das Nutzsignal $d_{\rm S}(t)$ ist formgleich mit der Energie–AKF des Sendeimulses $g(t)$. Das Matched-Filter bündelt die Energie um den geeigneten Zeitpunkt $T_{\rm D,\ opt}$.
(11) Mit welchem Rechteckimpuls $g(t)$ erreicht man mit dem entsprechend angepassten Filter das gleiche $\rho _{\rm MF}=50$ wie in Aufgabe (10)?
Mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=0.5$ oder mit $A_h=A_g=0.5,\ \Delta t_h=\Delta t_g=1$ ?
- Aus der Gleichung $\rho _{\rm MF} = 2 \cdot E_g/N_0$ geht bereits hervor, dass das SNR nur von der Energie $E_g$ des Eingangsimpulses abhängt und nicht von dessen Form.
- Der Exponentialimpuls mit $A_g=1,\ \Delta t_g=1$ hat die Energie $E_g=0.5$. Der Rechteckimpuls mit $A_g=1,\ \Delta t_g=0.5$ ebenfalls ⇒ $\rho _{\rm MF}=50$.
- Dagegen besitzt der Rechteckimpuls mit $A_g=0.5,\ \Delta t_g=1$ eine kleinere Energie ⇒ $E_g=0.25$ ⇒ $\rho _{\rm MF}=25$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} = 14$ dB.
Zur Handhabung des Applets
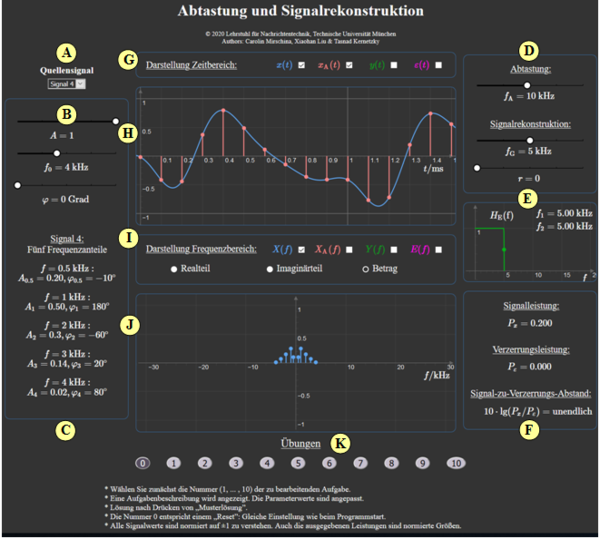
(A) Auswahl eines von vier Quellensignalen
(B) Parameterwahl für Quellensignal $1$ (Amplitude, Frequenz, Phase)
(C) Ausgabe der verwendeten Programmparameter
(D) Parameterwahl für Abtastung $(f_{\rm G})$ und
Signalrekonstruktion $(f_{\rm A},\ r)$
(E) Skizze des Empfänger–Frequenzgangs $H_{\rm E}(f)$
(F) Numerische Ausgabe $(P_x, \ P_{\rm \varepsilon}, \ 10 \cdot \lg(P_x/ P_{\rm \varepsilon})$
(G) Darstellungsauswahl für Zeitbereich
(H) Grafikbereich für Zeitbereich
( I ) Darstellungsauswahl für Frequenzbereich
(J) Grafikbereich für Frequenzbereich
(K) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2006 von Markus Elsberger im Rahmen seiner Diplomarbeit (LB) mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch die Exzellenzinitiative der TU München finanziell unterstützt. Wir bedanken uns.