Signaldarstellung/Spektralanalyse: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Als | + | Als $\text{spektralen Leckeffekt}$ bezeichnet man die Verfälschung des Spektrums eines periodischen und damit zeitlich unbegrenzten Signals aufgrund der impliziten Zeitbegrenzung der Diskreten Fouriertransformation $\rm (DFT)$. Dadurch werden zum Beispiel von einem Spektrumanalyzer |
*im Zeitsignal nicht vorhandene Frequenzanteile vorgetäuscht, und/oder | *im Zeitsignal nicht vorhandene Frequenzanteile vorgetäuscht, und/oder | ||
*tatsächlich vorhandene Spektralkomponenten durch Seitenkeulen verdeckt.}} | *tatsächlich vorhandene Spektralkomponenten durch Seitenkeulen verdeckt.}} | ||
| − | Das folgende $\text{Beispiel 1}$ wird zeigen, dass bei einem periodischen Signal die Anwendung der [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskreten Fouriertransformation]] (DFT) ohne Zusatzmaßnahmen nicht sinnvoll ist. Die Güte der Spektralanalyse – das heißt die Richtigkeit des gefundenen Spektrums – wird hier hauptsächlich durch die (mehr oder weniger geglückte) Anpassung der DFT-Parameter an die vorliegenden Signalparameter bestimmt. | + | Das folgende $\text{Beispiel 1}$ wird zeigen, dass bei einem periodischen Signal die Anwendung der [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskreten Fouriertransformation]] (DFT) ohne Zusatzmaßnahmen nicht sinnvoll ist. Die Güte der Spektralanalyse – das heißt die Richtigkeit des gefundenen Spektrums – wird hier hauptsächlich durch die (mehr oder weniger geglückte) Anpassung der DFT-Parameter an die vorliegenden Signalparameter bestimmt. |
| − | *Ist die Periodendauer $T_0$ des Signals bekannt, so sollte die Dauer $T_{\rm P}$ des für die DFT verwendeten Signalausschnittes ein ganzzahliges Vielfaches von $T_0$ betragen. Aufgabe der Spektralanalyse ist aber gerade das Auffinden beliebiger Signalanteile, so dass die Kenntnis von $T_0$ im allgemeinen nicht vorausgesetzt werden kann. | + | *Ist die Periodendauer $T_0$ des Signals bekannt, so sollte die Dauer $T_{\rm P}$ des für die DFT verwendeten Signalausschnittes ein ganzzahliges Vielfaches von $T_0$ betragen. Aufgabe der Spektralanalyse ist aber gerade das Auffinden beliebiger Signalanteile, so dass die Kenntnis von $T_0$ im allgemeinen nicht vorausgesetzt werden kann. |
| − | *Eine Maßnahme zur Verbesserung des Spektralanalyse ist die Fensterung mit einer „geeigneten” Zeitfunktion $w(t)$. Analysiert wird dann das Produktsignal $x(t) \cdot w(t)$. | + | *Eine Maßnahme zur Verbesserung des Spektralanalyse ist die Fensterung mit einer „geeigneten” Zeitfunktion $w(t)$. Analysiert wird dann das Produktsignal $x(t) \cdot w(t)$. |
*Aus der Literatur sind eine Vielzahl solcher Fensterfunktionen $w(t)$ bekannt, die je nach Aufgabenstellung zu guten oder weniger befriedigenden Ergebnissen führen. | *Aus der Literatur sind eine Vielzahl solcher Fensterfunktionen $w(t)$ bekannt, die je nach Aufgabenstellung zu guten oder weniger befriedigenden Ergebnissen führen. | ||
| − | Auf den nächsten Seiten wird der spektrale Leckeffekt an Beispielen verdeutlicht und es wird auf die Vorteile und Nachteile der verschiedenen Fensterfunktionen eingegangen. So viel vorneweg: '''Es gibt keine „beste” Fensterfunktion für alle Anwendungen'''. | + | Auf den nächsten Seiten wird der spektrale Leckeffekt an Beispielen verdeutlicht und es wird auf die Vorteile und Nachteile der verschiedenen Fensterfunktionen eingegangen. So viel vorneweg: '''Es gibt keine „beste” Fensterfunktion für alle Anwendungen'''. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| − | Die obere Grafik '''(a)''' aus [Söd93]<ref name='Söd93'>Söder, G.: | + | Die obere Grafik '''(a)''' aus [Söd93]<ref name='Söd93'>Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. In: Berlin – Heidelberg: Springer, 1993.</ref> zeigt das zeitdiskrete Signal $d(\nu)$ einer harmonischen Schwingung mit der Frequenz $f_0 = 125\,\text{ kHz}$ ⇒ Periodendauer $T_0 = 8 \,{\rm µ s}$. Der Abstand zweier aufeinanderfolgender Zeitabtastwerte ist bei diesem Beispiel zu $T_{\rm A} = 1 \,{\rm µ s}$ gewählt. |
| − | Rechts ist in logarithmierter Form (in dB) das frequenzdiskrete Spektrum $\vert D(\mu) \vert$ nach einer DFT mit $N = 32$ Abtastwerten dargestellt, woraus sich die weiteren DFT–Parameter wie folgt ergeben: | + | [[Datei:P_ID1160__Sig_T_5_4_S1_neu.png|right|frame|Beispiel für die Anwendung der Spektralanalyse]] |
| + | |||
| + | Rechts ist in logarithmierter Form (in dB) das frequenzdiskrete Spektrum $\vert D(\mu) \vert$ nach einer DFT mit $N = 32$ Abtastwerten dargestellt, woraus sich die weiteren DFT–Parameter wie folgt ergeben: | ||
*Dauer des Zeitausschnitts: $T_{\rm P} = 32 \,{\rm µ s}$, | *Dauer des Zeitausschnitts: $T_{\rm P} = 32 \,{\rm µ s}$, | ||
*Rasterung der Frequenzachse: $f_{\rm A} = 31.25 \,\text{ kHz}$. | *Rasterung der Frequenzachse: $f_{\rm A} = 31.25 \,\text{ kHz}$. | ||
| Zeile 34: | Zeile 36: | ||
Da hier durch die Intervallbreite $T_{\rm P}$ ein ganzzahliges Vielfaches der Periodendauer $T_0$ erfasst wird, liefert die DFT das richtige Ergebnis. Die beiden Diracfunktionen liegen genau bei $\pm4 \cdot f_{\rm A}$. | Da hier durch die Intervallbreite $T_{\rm P}$ ein ganzzahliges Vielfaches der Periodendauer $T_0$ erfasst wird, liefert die DFT das richtige Ergebnis. Die beiden Diracfunktionen liegen genau bei $\pm4 \cdot f_{\rm A}$. | ||
| − | + | Vermisst man mit der gleichen Anordnung eine Schwingung der Frequenz $f_0 = 109.375\,\text{ kHz}$ ⇒ Periodendauer $T_0 = 9.14 \,{\rm µ s}$ gemäß der unteren Grafik '''(b)''', so kommt es zu signifikanten Verfälschungen des Spektrums. | |
| − | |||
| − | Vermisst man mit der gleichen Anordnung eine Schwingung der Frequenz $f_0 = 109.375\,\text{ kHz}$ ⇒ Periodendauer $T_0 = 9.14 \,{\rm µ s}$ | ||
*Da nun $T_{\rm P}/T_0 = 3.5$ nicht mehr ganzzahlig ist, entstehen durch die periodische Fortsetzung des Zeitausschnittes Phasensprünge, in unserem Beispiel um $\pi$. | *Da nun $T_{\rm P}/T_0 = 3.5$ nicht mehr ganzzahlig ist, entstehen durch die periodische Fortsetzung des Zeitausschnittes Phasensprünge, in unserem Beispiel um $\pi$. | ||
| − | *Der Spektralbereich besteht nun nicht mehr aus zwei Diracfunktionen wie im Beispiel '''(a)''', sondern aus einer annähernd „kontinuierlichen” Frequenzfunktion mit dem Maximum in der Nähe der tatsächlichen Signalfrequenz und einer Reihe weiterer Anteile, die man '''Seitenkeulen''' (englisch: | + | *Der Spektralbereich besteht nun nicht mehr aus zwei Diracfunktionen wie im Beispiel '''(a)''', sondern aus einer annähernd „kontinuierlichen” Frequenzfunktion mit dem Maximum in der Nähe der tatsächlichen Signalfrequenz und einer Reihe weiterer Anteile, die man '''Seitenkeulen''' (englisch: "Side Lobes"') nennt.}} |
==Systemtheoretische Beschreibung der Fensterung== | ==Systemtheoretische Beschreibung der Fensterung== | ||
<br> | <br> | ||
| − | Das Zustandekommen solcher unerwünschter Seitenkeulen soll nun anhand der folgenden Grafik systemtheoretisch erklärt werden. Auch diese Grafik wurde dem Buch [Söd93]<ref name='Söd93'>Söder, G.: | + | Das Zustandekommen solcher unerwünschter Seitenkeulen soll nun anhand der folgenden Grafik systemtheoretisch erklärt werden. Auch diese Grafik wurde dem Buch [Söd93]<ref name='Söd93'>Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. In: Berlin – Heidelberg: Springer, 1993.</ref> entnommen. |
| − | [[Datei:P_ID1162__Sig_T_5_4_S2_neu.png| | + | [[Datei:P_ID1162__Sig_T_5_4_S2_neu.png|right|frame|Rechteck-Fenster und Bartlett-Fenster]] |
Betrachten Sie zunächst die obere Grafik '''(a)''' für das '''Rechteckfenster'''. | Betrachten Sie zunächst die obere Grafik '''(a)''' für das '''Rechteckfenster'''. | ||
| − | *Die in der DFT implizit enthaltene Zeitbegrenzung entspricht der Multiplikation des Signals $x(t)$ mit einer Rechteck–Fensterfunktion $w(t)$ der Höhe $1$ und der Dauer $T_{\rm P}$. Das linke obere Bild zeigt die zeitdiskrete Darstellung dieser Rechteckfunktion mit der normierten Zeitvariablen $\nu= t/T_{\rm A}$: | + | *Die in der DFT implizit enthaltene Zeitbegrenzung entspricht der Multiplikation des Signals $x(t)$ mit einer Rechteck–Fensterfunktion $w(t)$ der Höhe $1$ und der Dauer $T_{\rm P}$. |
| + | *Das linke obere Bild zeigt die zeitdiskrete Darstellung dieser Rechteckfunktion mit der normierten Zeitvariablen $\nu= t/T_{\rm A}$: | ||
:$${w} (\nu) = \left\{ \begin{array}{c} 1 \\ | :$${w} (\nu) = \left\{ \begin{array}{c} 1 \\ | ||
| Zeile 59: | Zeile 60: | ||
\end{array}$$ | \end{array}$$ | ||
| − | *Aus der Multiplikation $y(t) = x(t) \cdot w(t)$ des zu analysierenden Signals $x(t)$ und der Fensterfunktion $w(t)$ folgt für die Spektralfunktion $Y(f) = X(f) \ast W(f)$, wobei bei rechteckförmiger Fensterfunktion mit $f_{\rm A} = 1/T_{\rm P}$ gilt | + | *Aus der Multiplikation $y(t) = x(t) \cdot w(t)$ des zu analysierenden Signals $x(t)$ und der Fensterfunktion $w(t)$ folgt für die Spektralfunktion $Y(f) = X(f) \ast W(f)$, wobei bei rechteckförmiger Fensterfunktion mit $f_{\rm A} = 1/T_{\rm P}$ gilt. |
| + | *Die Funktion $W(f)$ ist in der rechten oberen Grafik in logarithmierter Form dargestellt: | ||
:$$W(f) = T_{\rm P} \cdot {\rm si}(\pi \cdot f \cdot T_{\rm P}) = {1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm}.$$ | :$$W(f) = T_{\rm P} \cdot {\rm si}(\pi \cdot f \cdot T_{\rm P}) = {1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm}.$$ | ||
| − | *Liegen alle Spektralanteile | + | *Liegen alle Spektralanteile von $x(t)$ im Frequenzraster $\mu \cdot f_{\rm A}$, so bleiben die frequenzdiskreten Spektralwerte $D(\mu )$ durch die Faltung mit $W(f)$ unverändert. |
*Andernfalls führt die Faltung mit $W(f)$ zu Verfälschungen, da die Nullstellen der $\rm si$–Funktion nun nicht mehr zu den diskreten Werten des Eingangsspektrums passen. | *Andernfalls führt die Faltung mit $W(f)$ zu Verfälschungen, da die Nullstellen der $\rm si$–Funktion nun nicht mehr zu den diskreten Werten des Eingangsspektrums passen. | ||
| Zeile 87: | Zeile 89: | ||
\hspace{0.2cm}W(f) ={1}/({2f_{\rm A}})\cdot {\rm si}^2(\pi \cdot | \hspace{0.2cm}W(f) ={1}/({2f_{\rm A}})\cdot {\rm si}^2(\pi \cdot | ||
{f}/({2f_{\rm A}}))\hspace{0.05cm}.$$ | {f}/({2f_{\rm A}}))\hspace{0.05cm}.$$ | ||
| − | *Durch die geringere Bewertung der bei unbegrenzten Signalen besonders problematischen Randbereiche hat das (logarithmisch gezeichnete) Spektrum $W(f)$ geringere Seitenschwinger als die $\rm si$–Funktion im oberen Bild, was zu geringeren Leckkomponenten führt. | + | *Durch die geringere Bewertung der bei unbegrenzten Signalen besonders problematischen Randbereiche hat das (logarithmisch gezeichnete) Spektrum $W(f)$ geringere Seitenschwinger als die $\rm si$–Funktion im oberen Bild, was zu geringeren Leckkomponenten führt. |
*Die bessere Unterdrückung der Seitenkeulen geht allerdings auf Kosten einer merkbaren Verkleinerung und Verbreiterung der Hauptkeule, wodurch das Auflösungsvermögen des Bartlett–Fensters gegenüber der Rechteck–Fensterung eingeschränkt wird. | *Die bessere Unterdrückung der Seitenkeulen geht allerdings auf Kosten einer merkbaren Verkleinerung und Verbreiterung der Hauptkeule, wodurch das Auflösungsvermögen des Bartlett–Fensters gegenüber der Rechteck–Fensterung eingeschränkt wird. | ||
| Zeile 107: | Zeile 109: | ||
*Beim Kaiser–Bessel–Fenster sind die Funktionen im Zeit– und Frequenzbereich jeweils für $\alpha = 3.5$ dargestellt. | *Beim Kaiser–Bessel–Fenster sind die Funktionen im Zeit– und Frequenzbereich jeweils für $\alpha = 3.5$ dargestellt. | ||
* ${\rm I}_0(.)$ bezeichnet die [https://de.wikipedia.org/wiki/Besselsche_Differentialgleichung Modifizierte Besselfunktion nullter Ordnung]. | * ${\rm I}_0(.)$ bezeichnet die [https://de.wikipedia.org/wiki/Besselsche_Differentialgleichung Modifizierte Besselfunktion nullter Ordnung]. | ||
| − | *Weitere Fensterfunktionen wie das Blackman–Harris–Fenster, das [https://de.wikipedia.org/wiki/Raised-Cosine-Filter Cosinus–Rolloff–Fenster] (auch Tukey–Fenster genannt) und noch viele andere mehr finden Sie im Buch [Söd93]<ref name='Söd93'>Söder, G.: | + | *Weitere Fensterfunktionen wie das Blackman–Harris–Fenster, das [https://de.wikipedia.org/wiki/Raised-Cosine-Filter Cosinus–Rolloff–Fenster] (auch Tukey–Fenster genannt) und noch viele andere mehr finden Sie im Buch [Söd93]<ref name='Söd93'>Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. In: Berlin – Heidelberg: Springer, 1993.</ref>. |
| Zeile 115: | Zeile 117: | ||
<br> | <br> | ||
[[Datei:P_ID1163__Sig_T_5_4_S4_v4.png|right|frame|Zusammenstellung wichtiger Gütekriterien von Fensterfunktionen]] | [[Datei:P_ID1163__Sig_T_5_4_S4_v4.png|right|frame|Zusammenstellung wichtiger Gütekriterien von Fensterfunktionen]] | ||
| − | Die Tabelle gibt Gütekriterien für die auf den letzten Seiten beschriebenen Fensterfunktionen wieder. Die Auswahl einer geeigneten Fensterfunktion sollte nach folgenden Gesichtspunkten erfolgen: | + | Die Tabelle gibt Gütekriterien für die auf den letzten Seiten beschriebenen Fensterfunktionen wieder. Die Auswahl einer geeigneten Fensterfunktion sollte nach folgenden Gesichtspunkten erfolgen: |
| − | *Der | + | *Der $\text{minimale Abstand zwischen Hauptkeule und Seitenkeulen}$ sollte möglichst groß sein, um den Einfluss des Leckeffektes gering zu halten und die Amplitudenauflösung zu verbessern. |
| − | *Aus Gründen einer guten Frequenzselektivität sollte die | + | *Aus Gründen einer guten Frequenzselektivität sollte die $\text{6dB–Bandbreite}$ gering sein. Ist diese zu groß, so überdeckt eine dominante Spektrallinie kleinere Anteile in der Umgebung. |
| − | *Der | + | *Der $\text{maximale Prozessverlust}$ (in dB) beinhaltet den maximalen Skalierungsfehler und die äquivalente Rauschbandbreite. Diese Größe sollte auf keinen Fall $\text{3.7 dB}$ überschreiten. |
| Zeile 126: | Zeile 128: | ||
<br clear=all> | <br clear=all> | ||
Nun werden die in der Tabelle angegebenen Gütekriterien etwas genauer beschrieben: | Nun werden die in der Tabelle angegebenen Gütekriterien etwas genauer beschrieben: | ||
| − | *Je größer der | + | *Je größer der $\text{minimale Haupt–zu–Seitenkeulen–Abstand}$ ⇒ Verhältnis der Hauptkeule zur höchsten Seitenkeule, desto besser ist die Amplitudenauflösung einer Fensterfunktion. Beim Rechteck ist dieser Abstand erwartungsgemäß am kleinsten $\text{(13 dB)}$. Das beste Ergebnis liefert mit $\text{92 dB}$ das Blackman–Harris–Fenster vierter Ordnung. |
| − | *Da jedoch nicht nur die höchste, sondern auch alle weiteren Seitenkeulen zum Leckeffekt beitragen, ist der | + | |
| − | + | *Da jedoch nicht nur die höchste, sondern auch alle weiteren Seitenkeulen zum Leckeffekt beitragen, ist der $\text{Seitenkeulenabfall}$ ein weiteres Maß für das Auflösungsvermögen. Von den angegebenen Fensterfunktionen weisen diesbezüglich das Hanning–Fenster sowie das Cosinus–Rolloff–Fenster mit Rolloff $r = 0.5$ die günstigsten Werte auf $\text{(18 dB/Oktave)}$. | |
| + | [[Datei:P_ID1164__Sig_T_5_4_S4b_neu.png|left|frame|Zur Verdeutlichung der $\text{6 dB}$-Bandbreite]] | ||
| + | *Die $\text{6 dB–Bandbreite}$, die aus der logarithmierten Spektralfunktion abgelesen werden kann, ist ein wichtiges Maß für das Frequenzauflösungsvermögen. Zwei im Signal vorhandene Anteile bei $f_1$ und $f_2$ können nur dann aufgelöst werden, wenn die Differenz $f_2 - f_1$ größer als die $\text{6 dB}$–Bandbreite der verwendeten Fensterfunktion ist (siehe linke Grafik). | ||
| − | + | *Die $\text{Fensterfläche}$ der Funktion $w(t)$ gibt zugleich die Höhe $W(0)$ im Spektralbereich an. Bei allen Fenstern außer dem Rechteck ergibt sich aufgrund der Unterdrückung der äußeren Abtastwerte eine Fensterfläche kleiner $1$ und damit ein Fehler in der Amplitude des DFT–Ergebnisses, der jedoch bei Kenntnis von $w(t)$ vollständig korrigierbar ist. | |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ | $\text{Fazit:}$ | ||
| − | *Ein guter Kompromiss ist das | + | *Ein guter Kompromiss ist das $\text{Hanning–Fenster}$ (in der Tabelle blau hervorgehoben), das bezüglich der drei Hauptkriterien (rote Markierungen) nie mit „Grau” abschneidet. |
| − | *Das | + | |
| + | *Das $\text{Hamming–Fenster}$ unterscheidet sich hiervon im Zeitbereich nur geringfügig, aber im Spektralbereich beträchtlich. So beträgt der Seitenkeulenabfall pro Oktave nur mehr $\text{6 dB}$ $($statt $\text{18 dB})$.}} | ||
Version vom 18. Mai 2021, 17:52 Uhr
Inhaltsverzeichnis
Spektraler Leckeffekt
$\text{Definition:}$ Als $\text{spektralen Leckeffekt}$ bezeichnet man die Verfälschung des Spektrums eines periodischen und damit zeitlich unbegrenzten Signals aufgrund der impliziten Zeitbegrenzung der Diskreten Fouriertransformation $\rm (DFT)$. Dadurch werden zum Beispiel von einem Spektrumanalyzer
- im Zeitsignal nicht vorhandene Frequenzanteile vorgetäuscht, und/oder
- tatsächlich vorhandene Spektralkomponenten durch Seitenkeulen verdeckt.
Das folgende $\text{Beispiel 1}$ wird zeigen, dass bei einem periodischen Signal die Anwendung der Diskreten Fouriertransformation (DFT) ohne Zusatzmaßnahmen nicht sinnvoll ist. Die Güte der Spektralanalyse – das heißt die Richtigkeit des gefundenen Spektrums – wird hier hauptsächlich durch die (mehr oder weniger geglückte) Anpassung der DFT-Parameter an die vorliegenden Signalparameter bestimmt.
- Ist die Periodendauer $T_0$ des Signals bekannt, so sollte die Dauer $T_{\rm P}$ des für die DFT verwendeten Signalausschnittes ein ganzzahliges Vielfaches von $T_0$ betragen. Aufgabe der Spektralanalyse ist aber gerade das Auffinden beliebiger Signalanteile, so dass die Kenntnis von $T_0$ im allgemeinen nicht vorausgesetzt werden kann.
- Eine Maßnahme zur Verbesserung des Spektralanalyse ist die Fensterung mit einer „geeigneten” Zeitfunktion $w(t)$. Analysiert wird dann das Produktsignal $x(t) \cdot w(t)$.
- Aus der Literatur sind eine Vielzahl solcher Fensterfunktionen $w(t)$ bekannt, die je nach Aufgabenstellung zu guten oder weniger befriedigenden Ergebnissen führen.
Auf den nächsten Seiten wird der spektrale Leckeffekt an Beispielen verdeutlicht und es wird auf die Vorteile und Nachteile der verschiedenen Fensterfunktionen eingegangen. So viel vorneweg: Es gibt keine „beste” Fensterfunktion für alle Anwendungen.
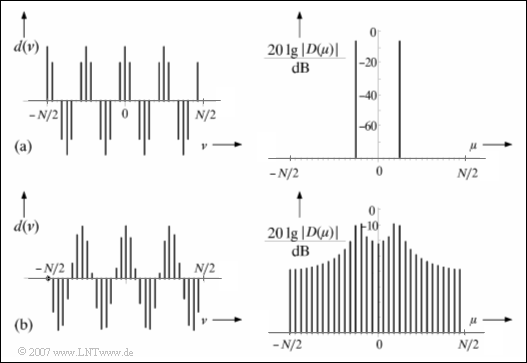
$\text{Beispiel 1:}$ Die obere Grafik (a) aus [Söd93][1] zeigt das zeitdiskrete Signal $d(\nu)$ einer harmonischen Schwingung mit der Frequenz $f_0 = 125\,\text{ kHz}$ ⇒ Periodendauer $T_0 = 8 \,{\rm µ s}$. Der Abstand zweier aufeinanderfolgender Zeitabtastwerte ist bei diesem Beispiel zu $T_{\rm A} = 1 \,{\rm µ s}$ gewählt.
Rechts ist in logarithmierter Form (in dB) das frequenzdiskrete Spektrum $\vert D(\mu) \vert$ nach einer DFT mit $N = 32$ Abtastwerten dargestellt, woraus sich die weiteren DFT–Parameter wie folgt ergeben:
- Dauer des Zeitausschnitts: $T_{\rm P} = 32 \,{\rm µ s}$,
- Rasterung der Frequenzachse: $f_{\rm A} = 31.25 \,\text{ kHz}$.
Da hier durch die Intervallbreite $T_{\rm P}$ ein ganzzahliges Vielfaches der Periodendauer $T_0$ erfasst wird, liefert die DFT das richtige Ergebnis. Die beiden Diracfunktionen liegen genau bei $\pm4 \cdot f_{\rm A}$.
Vermisst man mit der gleichen Anordnung eine Schwingung der Frequenz $f_0 = 109.375\,\text{ kHz}$ ⇒ Periodendauer $T_0 = 9.14 \,{\rm µ s}$ gemäß der unteren Grafik (b), so kommt es zu signifikanten Verfälschungen des Spektrums.
- Da nun $T_{\rm P}/T_0 = 3.5$ nicht mehr ganzzahlig ist, entstehen durch die periodische Fortsetzung des Zeitausschnittes Phasensprünge, in unserem Beispiel um $\pi$.
- Der Spektralbereich besteht nun nicht mehr aus zwei Diracfunktionen wie im Beispiel (a), sondern aus einer annähernd „kontinuierlichen” Frequenzfunktion mit dem Maximum in der Nähe der tatsächlichen Signalfrequenz und einer Reihe weiterer Anteile, die man Seitenkeulen (englisch: "Side Lobes"') nennt.
Systemtheoretische Beschreibung der Fensterung
Das Zustandekommen solcher unerwünschter Seitenkeulen soll nun anhand der folgenden Grafik systemtheoretisch erklärt werden. Auch diese Grafik wurde dem Buch [Söd93][1] entnommen.
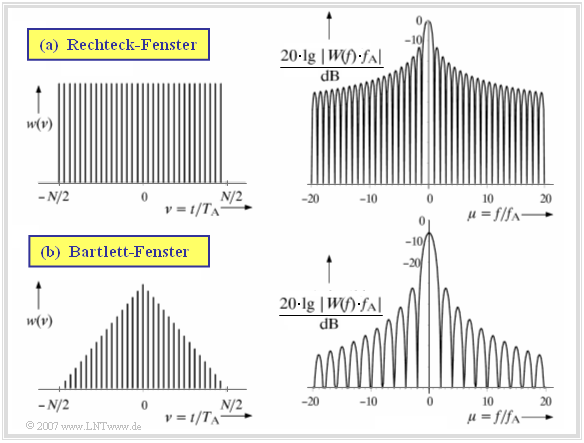
Betrachten Sie zunächst die obere Grafik (a) für das Rechteckfenster.
- Die in der DFT implizit enthaltene Zeitbegrenzung entspricht der Multiplikation des Signals $x(t)$ mit einer Rechteck–Fensterfunktion $w(t)$ der Höhe $1$ und der Dauer $T_{\rm P}$.
- Das linke obere Bild zeigt die zeitdiskrete Darstellung dieser Rechteckfunktion mit der normierten Zeitvariablen $\nu= t/T_{\rm A}$:
- $${w} (\nu) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$
- Aus der Multiplikation $y(t) = x(t) \cdot w(t)$ des zu analysierenden Signals $x(t)$ und der Fensterfunktion $w(t)$ folgt für die Spektralfunktion $Y(f) = X(f) \ast W(f)$, wobei bei rechteckförmiger Fensterfunktion mit $f_{\rm A} = 1/T_{\rm P}$ gilt.
- Die Funktion $W(f)$ ist in der rechten oberen Grafik in logarithmierter Form dargestellt:
- $$W(f) = T_{\rm P} \cdot {\rm si}(\pi \cdot f \cdot T_{\rm P}) = {1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm}.$$
- Liegen alle Spektralanteile von $x(t)$ im Frequenzraster $\mu \cdot f_{\rm A}$, so bleiben die frequenzdiskreten Spektralwerte $D(\mu )$ durch die Faltung mit $W(f)$ unverändert.
- Andernfalls führt die Faltung mit $W(f)$ zu Verfälschungen, da die Nullstellen der $\rm si$–Funktion nun nicht mehr zu den diskreten Werten des Eingangsspektrums passen.
Die durch Begrenzung und periodische Fortsetzung entstehendenen Unstetigkeiten im Zeitbereich werden vermindert, wenn statt der konstanten Eins–Bewertung durch das Rechteck die beiden Randbereiche des Fensters schwächer gewichtet werden als die Mitte.
Betrachten Sie dazu die untere Grafik (b) für das Bartlett–Fenster – auch Dreieckfenster genannt:
- Die zeitdiskrete Beschreibung des Bartlett–Fensters lautet mit $\nu = t/T_{\rm A}$:
- $${w} (\nu) = \left\{ \begin{array}{c} 1 - {2 \hspace{0.05cm} \cdot \hspace{0.05cm} |\nu|}/{N} \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$
- Daraus folgt für die zeitkontinuierliche Fensterfunktion $w(t)$ und die Spektraldarstellung $W(f)$:
- $${w} (t) = \left\{ \begin{array}{c} 1 -{|t|}/{(T_{\rm P}/2)} \\ 0 \\ \end{array} \right.\hspace{0.05cm} \begin{array}{*{20}c} |t| \le T_{\rm P}/2\\ {\rm sonst} \\ \end{array}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm}W(f) ={1}/({2f_{\rm A}})\cdot {\rm si}^2(\pi \cdot {f}/({2f_{\rm A}}))\hspace{0.05cm}.$$
- Durch die geringere Bewertung der bei unbegrenzten Signalen besonders problematischen Randbereiche hat das (logarithmisch gezeichnete) Spektrum $W(f)$ geringere Seitenschwinger als die $\rm si$–Funktion im oberen Bild, was zu geringeren Leckkomponenten führt.
- Die bessere Unterdrückung der Seitenkeulen geht allerdings auf Kosten einer merkbaren Verkleinerung und Verbreiterung der Hauptkeule, wodurch das Auflösungsvermögen des Bartlett–Fensters gegenüber der Rechteck–Fensterung eingeschränkt wird.
Spezielle Fensterfunktionen
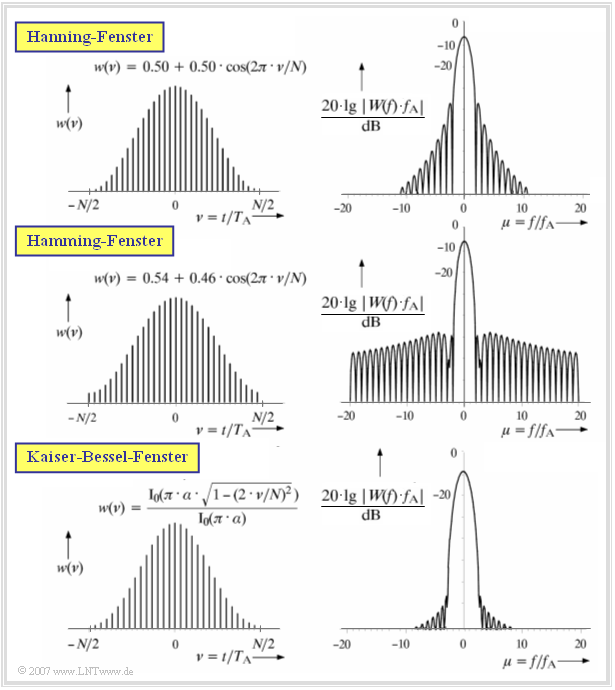
Nun werden einige häufig eingesetzte Fensterfunktionen, nämlich
- das Hanning–Fenster,
- das Hamming–Fenster und
- das Kaiser–Bessel–Fenster
anhand von Grafiken und darin enthaltenen Gleichungen beschrieben. Für die Laufvariable im Zeitbereich gilt stets $–N/2 ≤ \nu < N/2$.
Hinweise:
- Beim Kaiser–Bessel–Fenster sind die Funktionen im Zeit– und Frequenzbereich jeweils für $\alpha = 3.5$ dargestellt.
- ${\rm I}_0(.)$ bezeichnet die Modifizierte Besselfunktion nullter Ordnung.
- Weitere Fensterfunktionen wie das Blackman–Harris–Fenster, das Cosinus–Rolloff–Fenster (auch Tukey–Fenster genannt) und noch viele andere mehr finden Sie im Buch [Söd93][1].
Die Eignung dieser Fensterfunktionen für verschiedenartige Aufgaben der Spektralanalyse nennen wir auf der nächsten Seite.
Gütekriterien von Fensterfunktionen
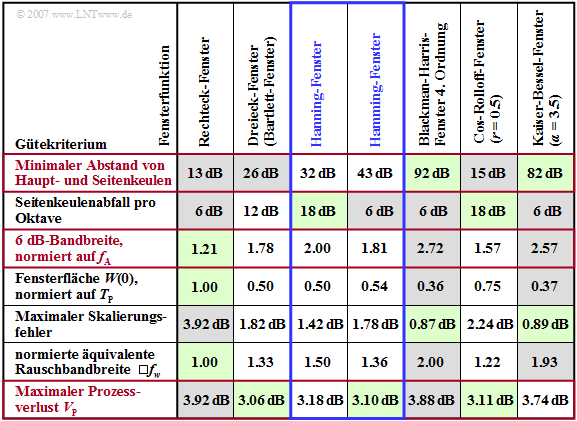
Die Tabelle gibt Gütekriterien für die auf den letzten Seiten beschriebenen Fensterfunktionen wieder. Die Auswahl einer geeigneten Fensterfunktion sollte nach folgenden Gesichtspunkten erfolgen:
- Der $\text{minimale Abstand zwischen Hauptkeule und Seitenkeulen}$ sollte möglichst groß sein, um den Einfluss des Leckeffektes gering zu halten und die Amplitudenauflösung zu verbessern.
- Aus Gründen einer guten Frequenzselektivität sollte die $\text{6dB–Bandbreite}$ gering sein. Ist diese zu groß, so überdeckt eine dominante Spektrallinie kleinere Anteile in der Umgebung.
- Der $\text{maximale Prozessverlust}$ (in dB) beinhaltet den maximalen Skalierungsfehler und die äquivalente Rauschbandbreite. Diese Größe sollte auf keinen Fall $\text{3.7 dB}$ überschreiten.
Diese wichtigsten Gütekriterien sind in nebenstehender Tabelle durch rote Schrift hervorgehoben.
- In jeder Zeile sind eher günstige Fensterfunktionen grün und eher ungünstigste grau hinterlegt.
- Aus der Verteilung der grünen und grauen Flächen ist bereits ersichtlich, dass es die optimale Fensterfunktion nicht gibt.
Nun werden die in der Tabelle angegebenen Gütekriterien etwas genauer beschrieben:
- Je größer der $\text{minimale Haupt–zu–Seitenkeulen–Abstand}$ ⇒ Verhältnis der Hauptkeule zur höchsten Seitenkeule, desto besser ist die Amplitudenauflösung einer Fensterfunktion. Beim Rechteck ist dieser Abstand erwartungsgemäß am kleinsten $\text{(13 dB)}$. Das beste Ergebnis liefert mit $\text{92 dB}$ das Blackman–Harris–Fenster vierter Ordnung.
- Da jedoch nicht nur die höchste, sondern auch alle weiteren Seitenkeulen zum Leckeffekt beitragen, ist der $\text{Seitenkeulenabfall}$ ein weiteres Maß für das Auflösungsvermögen. Von den angegebenen Fensterfunktionen weisen diesbezüglich das Hanning–Fenster sowie das Cosinus–Rolloff–Fenster mit Rolloff $r = 0.5$ die günstigsten Werte auf $\text{(18 dB/Oktave)}$.
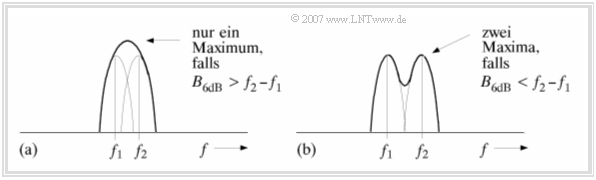
- Die $\text{6 dB–Bandbreite}$, die aus der logarithmierten Spektralfunktion abgelesen werden kann, ist ein wichtiges Maß für das Frequenzauflösungsvermögen. Zwei im Signal vorhandene Anteile bei $f_1$ und $f_2$ können nur dann aufgelöst werden, wenn die Differenz $f_2 - f_1$ größer als die $\text{6 dB}$–Bandbreite der verwendeten Fensterfunktion ist (siehe linke Grafik).
- Die $\text{Fensterfläche}$ der Funktion $w(t)$ gibt zugleich die Höhe $W(0)$ im Spektralbereich an. Bei allen Fenstern außer dem Rechteck ergibt sich aufgrund der Unterdrückung der äußeren Abtastwerte eine Fensterfläche kleiner $1$ und damit ein Fehler in der Amplitude des DFT–Ergebnisses, der jedoch bei Kenntnis von $w(t)$ vollständig korrigierbar ist.
$\text{Fazit:}$
- Ein guter Kompromiss ist das $\text{Hanning–Fenster}$ (in der Tabelle blau hervorgehoben), das bezüglich der drei Hauptkriterien (rote Markierungen) nie mit „Grau” abschneidet.
- Das $\text{Hamming–Fenster}$ unterscheidet sich hiervon im Zeitbereich nur geringfügig, aber im Spektralbereich beträchtlich. So beträgt der Seitenkeulenabfall pro Oktave nur mehr $\text{6 dB}$ $($statt $\text{18 dB})$.
Maximaler Prozessverlust
Dieses kombinierte Gütekriterium berücksichtigt den maximalen Skalierungsfehler ebenso wie die (normierte) äquivalente Rauschbandbreite. Der maximale Prozessverlust wird meist in $\text{dB}$ angegeben und sollte entsprechend seines Namens eher klein sein:
- $$10 \cdot {\rm lg}\hspace{0.15cm}V_{\rm P}\hspace{0.15cm}{\rm (in}\hspace{0.15cm}{\rm dB)}= 20 \cdot {\rm lg}\hspace{0.15cm} \frac{|W(f=0)|}{|W(f=f_{\rm A}/2)|} + 10 \cdot {\rm lg}\hspace{0.15cm} \frac{\int_{-\infty}^{\infty}|W(f)|^2\hspace{0.05cm}{\rm d}f}{f_{\rm A} \cdot |W(f=0)|^2} \hspace{0.05cm}.$$
Aus der Tabelle erkennt man, dass $V_{\rm P}$ für die betrachteten Fensterfunktionen Werte zwischen $\text{3 dB}$ und $\text{4 dB}$ annimmt, wobei Fensterfunktionen mit $V_{\rm P} > 3.7 \,\text{dB}$ (Rechteck, Blackman–Harris, Kaiser–Bessel) nicht verwendet werden sollten. Gerade diese sind aber bezüglich des Haupt–zu–Seitenkeulen–Abstands am besten.
Die beiden Anteile sind wie folgt zu interpretieren:
- Der maximale Skalierungsfehler ist das Verhältnis, um das sich die mit der DFT ermittelte Amplitude von der tatsächlichen Signalamplitude unterscheidet. Der Amplitudenfehler aufgrund einer Fensterfläche kleiner als $1$ wird dabei als korrigiert vorausgesetzt.
- Je breiter die Hauptkeule der Fensterfunktion ist, um so kleiner ist dieser Skalierungsfehler. Der Fehler ist am größten, wenn die Frequenz $f_0$ einer harmonischen Schwingung in der Mitte zwischen zwei DFT–Stützstellen liegt ⇒ Quotient $|W(f = 0)| / |W(f = f_{\rm A}/2)|$.
- Die äquivalente Rauschbandbreite der verwendeten Fensterfunktion – berechenbar als Breite des flächengleichen Rechtecks bezüglich dem Betragsquadrat $|W(f)|^2$ der Spektralfunktion – erfasst den störenden Einfluss von weißem Rauschen und sollte möglichst gering sein.
- Die kleinste Rauschbandbreite ergibt sich für das Rechteck. Alle anderen Fensterfunktionen besitzen eine größere Rauschbandbreite und damit bei Vorhandensein von Rauschstörungen auch ein (deutlich) ungünstigeres Signal–zu–Rausch–Leistungsverhältnis.
$\text{Fazit:}$ Die Ergebnisse dieses Abschnitts können wie folgt zusammengefasst werden:
- Eine ideale Fensterfunktion gibt es nicht. Je nach Aufgabenstellung (gute Amplituden– bzw. Frequenzauflösung) liefern unterschiedliche Fenster das jeweils beste Ergebnis. Zu empfehlen ist deshalb, dass man zur Spektralanalyse stets mehrere Fensterfunktionen heranzieht oder zumindest eine Fensterfunktion mit verschiedenen Parametern verwendet.
- Ein tragbarer Kompromiss hinsichtlich aller Kriterien ist das Hamming–Fenster, das lediglich beim Seitenkeulenabfall $($nur $\text{6 dB pro Oktave})$ einen ungünstigen Wert liefert. Obwohl sich das Hanning–Fenster im Zeitbereich vom Hamming-Fenster nur mariginal unterscheidet, ist im Spektralbereich (minimaler Abstand zwischen Hauptkeule und Seitenkeulen) der Unterschied zwischen beiden beträchtlich.
Aufgaben zum Kapitel
Aufgabe 5.4: Vergleich von Rechteck– und Hanningfenster
Aufgabe 5.4Z: Zum Hanning-Fenster