Aufgaben:Aufgabe 3.4: Entropie für verschiedene Wahrscheinlichkeiten: Unterschied zwischen den Versionen
Aus LNTwww
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 28: | Zeile 28: | ||
<quiz display=simple> | <quiz display=simple> | ||
| + | {Zu welcher Entropie führt $P_X(X) = [ 0.1, 0.2, 0.3, 0.4]$ ? | ||
| + | |type="{}"} | ||
| + | $H_a(X)$ = { 1.846 1% } | ||
| + | |||
| + | {Es gelte allgemein $P_X(X) = [ 0.1, 0.2, p_3, p_4]$. | ||
| + | |type="{}"} | ||
| − | |||
| − | |||
| − | |||
Version vom 24. November 2016, 17:52 Uhr
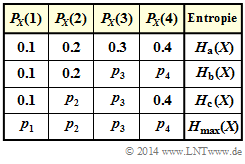
In der ersten Zeile der nebenstehenden Tabelle ist die mit „a” bezeichnete Wahrscheinlichkeitsfunktion angegeben. Für dieses $P_X(X)$ soll soll in der Teilaufgabe (a) die Entropie
$$H_{\rm a}(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ]$$
berechnet werden. Da hier der Logarithmus zur Basis 2 verwendet wird, ist die Pseudo–Einheit „bit” anzufügen.
In den weiteren Aufgaben sollen jeweils einige Wahrscheinlichkeiten variiert werden und zwar derart, dass sich jeweils die größtmögliche Entropie ergibt:
- Durch geeignete Variation von $p_3$ und $p_4$ kommt man zur maximalen Entropie $H_b(X)$ unter der Voraussetzung $p_1 = 0.1$ und $p_2 = 0.2$ $\Rightarrow$ Teilaufgabe (b).
- Durch geeignete Variation von $p_2$ und $p_3$ kommt man zur maximalen Entropie $H_c(X)$ unter der Voraussetzung $p_1 = 0.1$ und $p_4 = 0.4$ $\Rightarrow$ Teilaufgabe (c).
- In der Teilaufgabe (d) sind alle vier Parameter zur Variation freigegeben, die entsprechend der maximalen Entropie $\Rightarrow$ $H_{max}(X)$ zu bestimmen sind.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 3.1
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.