Aufgaben:Aufgabe 3.5Z: Nochmals Kullback-Leibler-Distanz

• Zurück zum Buch

Die Wahrscheinlichkeitsfunktion lautet:

$$P_Y(X) = [\hspace{0.03cm}0.25\hspace{0.03cm}, \hspace{0.03cm} 0.25\hspace{0.03cm},\hspace{0.03cm} 0.25 \hspace{0.03cm}, \hspace{0.03cm} 0.25\hspace{0.03cm}]\hspace{0.05cm}$$ Die Zufallsgröße $X$ ist also gekennzeichnet

• durch den Symbolumfang $M=4$,
• mit gleichen Wahrscheinlichkeiten.

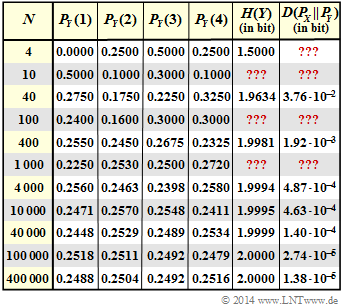
Die Zufallsgröße $Y$ ist stets eine Näherung für $X$. Sie wurde per Simulation aus einer Gleichverteilung gewonnen, wobei jeweils nur $N$ Zufallswerte ausgewertet wurden. Das heißt: $P_Y(1)$,...,$P_Y(4)$ sind im herkömmlichen Sinn keine Wahrscheinlichkeiten. Sie beschreiben vielmehr relative Häufigkeiten.

Das Ergebnis der sechsten Versuchsreihe (mit $N=1000$) ird demnach durch die folgende Wahrscheinlichkeitsfunktion zusammengefasst:

$$P_Y(X) = [\hspace{0.05cm}0.225\hspace{0.05cm}, \hspace{0.05cm} 0.253\hspace{0.05cm},\hspace{0.05cm} 0.250 \hspace{0.05cm}, \hspace{0.05cm} 0.272\hspace{0.05cm}] \hspace{0.05cm}$$ Bei dieser Schreibweise ist bereits berücksichtigt, dass die Zufallsgrößen $X$ und $Y$ auf dem gleichen Alphabet $X =$ {1, 2, 3, 4} basieren.

Mit diesen Voraussetzungen gilt für die relative Entropie (englisch: Informational Divergence) zwischen den Wahrscheinlichkeitsfunktionen $P_X(.)$ und $P_Y(.)$ :

$D( P_X || P_Y) = E_X [ log_2 \frac{P_X(X)}{P_Y(Y)}] = \sum\limits_{\mu=1}^M P_X(\mu) . log_2 \frac{P_X(\mu)}{P_Y(\mu)}$

Man bezeichnet $D( P_X || P_Y)$ als Kullback–Leibler–Distanz. Diese ist ein Maß für die Ähnlichkeit zwischen den beiden Wahrscheinlichkeitsfunktionen $P_X(.)$ und $P_Y(.)$. Die Erwartungswertbildung geschieht hier hinsichtlich der (tatsächlich gleichverteilten) Zufallsgröße $X$. Dies wird durch die Nomenklatur $E_X[.]$ angedeutet.

Eine zweite Form der Kullback–Leibler–Distanz ergibt sich durch die Erwartungswertbildung hinsichtlich der Zufallsgröße $Y \Rightarrow E_Y[.]$:

$D( P_Y || P_X) = E_Y [ log_2 \frac{P_Y(Y)}{P_Y(Y)}] = \sum\limits_{\mu=1}^M P_Y(\mu) . log_2 \frac{P_Y(\mu)}{P_X(\mu)}$

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 3.1 dieses Buches. Die Angaben der Entropie $H(Y)$ und der Kullback–Leibler–Distanz $D( P_X || P_Y)$ in obiger Grafik sind in „bit” zu verstehen. die mit „???" versehenen Felder sollen von Ihnen in dieser Aufgabe ergänzt werden.

Fragebogen

1

Welche Entropie besitzt die Zufallsgröße $X$ ?

$H(X)$ = $bit$

2

Wie groß sind die Entropien der Zufallsgrößen $Y$ (Näherungen für $X$)?

$N=1000$ : $H(Y)$ = $bit$

$N=100$ : $H(Y)$ = $bit$

$N=10$ : $H(Y)$ = $bit$

3

Berechnen Sie die folgenden Kullback–Leibler–Distanzen.

$N=1000$ : $D( P_X || P_Y)$ = . 10 ( )$bit$

$N=100$ : $D( P_X || P_Y)$= . 10 ( )$bit$

$N=10$ : $D( P_X || P_Y)$= . 10 ( )$bit$

4

Liefert $D(P_Y||P_X)$ jeweils exakt das gleiche Ergebnis?

	Falsch
	Richtig

5

Welche Aussagen gelten für die Kullback–Leibler–Distanzen bei $N = 4$?

	Es gilt $D(P_X||P_Y) = 0$.
	Es gilt $D(P_X||P_Y) = 0.5 bit$
	$D(P_X||P_Y)$ ist unendlich groß
	Es gilt $D(P_Y||P_X) = 0$.
	Es gilt $D(P_Y||P_X) = 0.5 bit$.
	$D(P_Y||P_X)$ ist unendlich groß.

6

Ändern sich $H(Y)$ und $D(P_X||P_Y)$monoton mit $N$?

	Falsch
	Richtig

Musterlösung

Musterlösung

1.Bei gleichen Wahrscheinlichkeiten gilt mit $M = 4$ :

$H(X) = log_2 M = 2 (bit)$

2. Die Wahrscheinlichkeiten für die empirisch ermittelten Zufallsgrößen $Y$ weichen im Allgemeinen (nicht immer!) von der Gleichverteilung um so mehr ab, je kleiner der Parameter $N$ ist. Man erhält

• $N = 1000 \Rightarrow P_Y(Y) = [0.225, 0.253, 0.250, 0.272]$ :

$H(Y) = 0.225 . log_2 \frac{1}{0.225} +0.253. log_2 \frac{1}{0.253} + 0.250 . log_2 \frac{1}{0.250}+ 0.272 . log_2 \frac{1}{0.272} = 1.9968 (bit)$

3. 4. 5. 6. 7.